基于磁控制的双谐振腔LLC 谐振变换器*

郑 宏，严序文，袁雪凯，秦润田，尤涛

(江苏大学电气信息工程学院,江苏 镇江 212013)

随着世界化石能源的日益减少,光伏发电、风力发电等新能源技术受到了越来越多的关注,但目前这些新能源发电单元受气候、天气等外部条件的影响较大,输出电能不稳定、不连续,输出电压范围较宽,因此就需要一款在宽输入电压下仍能高效运行的后级隔离型变换器。[1-2]而在一系列DC-DC 变换器结构中,全桥LLC 谐振变换器能够在全电压范围内,实现原边MOS 管的零电压开通(Zero Voltage Switching,ZVS)和副边整流管的零电流关断(Zero Current Switching,ZCS)[3],开关损耗低,效率较高,同时又具有无功环流较小的特性,因此被广泛应用于该领域。

传统的LLC 谐振变换器通常采用变频控制或移相控制来调节输出电压。当输入电压范围较宽时,变频调控需要较宽的频率变化范围,不利于磁性元件的优化设计,从而导致变换器的效率较低。移相控制技术目前也受到了广泛应用,它具有开关频率固定、控制电路结构简单等优点,可以在较宽的输入电压范围下调节变换器的电压增益,但它的电压增益比只能低于1,并且移相角不宜过大,否则就会引起变换器的原副边电流应力增大、无功环流增大等问题,从而导致变换器的效率低下[4]。

针对以上问题,文献[2]提出一种将可变倍频技术和Burst 控制模式相结合的方法,将输入电压的高低电压比增大到4∶1,虽然该方法大大拓宽了输入电压范围,但控制电路结构复杂,且在轻载时效率较低。

文献[3]提出一种混合模式控制的LLC 变换器,副边两个整流管被换成了开关管。在高输入电压下,采用移相控制技术改变开关管的电压增益,以此来达到稳压的目的,记为Buck 模式；当输入电压较低时,通过控制副边开关管的共同导通时间来提升变换器的电压增益,稳定输出电压,记为Boost 模式。但是当变换器工作在Buck 模式下,变换器就存在一个周期没有能量直接传到副边,且变换器的原边环流较大,效率较低。并且变换器增加了两个开关管,需要额外的控制电路,增加了成本,也降低了效率。文献[4]提出了一种Boost 集成型LLC 谐振变换器,它在桥臂中间增加了两个Boost 输入电感,一定程度上增大了变换器的电压增益,但所提变换器只有在输入电压在中间值附近时,变换器的工作特性最优。

本文在拓扑和控制方法上作出改进,提出一种将磁控制的可变电感技术和全桥双谐振腔LLC 谐振变换器(Full-Bridge Double Resonant Tank,FBDRT)相结合的新方案。首先介绍了全桥双谐振[5]LLC 谐振变换器的工作原理及其能够降低电压增益需求的原因,然后分析了如何将可变电感技术与之相结合。目前可变电感技术已经被广泛应用在电子镇流器、LED 驱动电源等领域。在谐振变换器中,可变电感通过反馈输出电压来改变压控电流源的电流,从而改变磁芯磁导率来控制磁芯的饱和程度,以达到调节电感的目的,从而能够调节电压增益来稳定输出电压[6]。

1 工作原理分析

基于磁控制的FBDRT LLC 谐振变换器如图1所示。开关管S1～S4组成全桥逆变网络,复合可变电感Lr,谐振电容Cr1、Cr2以及变压器励磁电感Lm1、Lm2共同构成双谐振腔结构,两个相同的变压器将变换器的原副边隔离开,副边的桥式整流电路由D1～D4组成。可变电感的Lr的主绕组为Nac,附加绕组为N1、N2,反馈控制回路通过控制压控电流源的直流偏置电流Idc来实现电感量的控制。

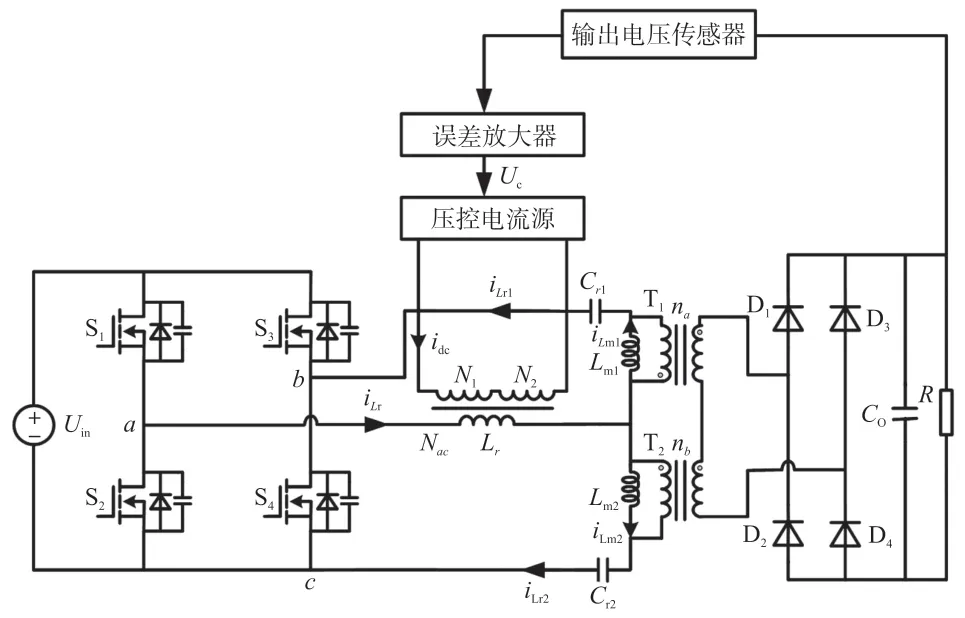
图1 基于磁控制的FBDRT LLC 谐振变换器

1.1 电路拓扑原理分析

FBDRT LLC 变换器在全桥LLC 谐振变换器的基础上多增加了一个谐振腔,如图2 所示,方波发生网络中的S1、S4和S2、S3开关管以0.5 的占空比交替互补导通,那么Uab是占空比为0.5,峰值为±Uin的方波；Uac是占空比为0.5,峰值为±Uin/0 的方波,但Uac存在直流偏置电压0.5Uin。为了便于变换器的模态分析,现假设:

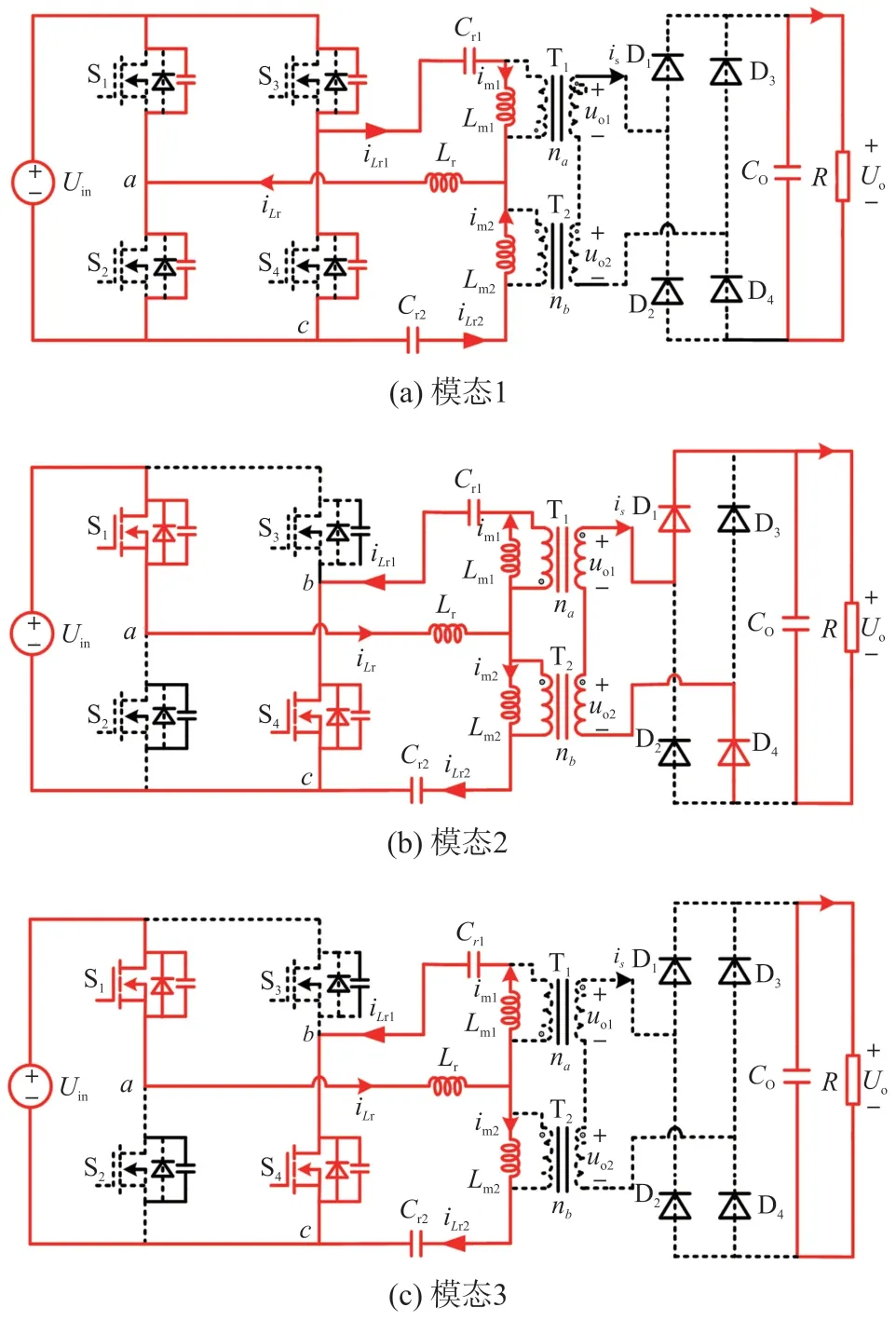
图2 FBDRT LLC 谐振变换器的工作模态

(1)原边开关管、副边整流二极管均为理想开关管。

(2)开关管S1～S4的寄生电容大小相等,记为Coss。

(3)谐振电容Cr1、Cr2相同,即Cr1＝Cr2＝0.5Cr。

(4)励磁电感Lm1、Lm2相同,即Lm1＝Lm2＝2Lm。

(5)两变压器匝比na、nb相同,na＝nb＝2ne。

设计时,为了降低开关损耗,将变换器设计工作在ZVS 区域,即fs＜fr-min,典型工作波形如图3 所示。所提电路拓扑在fs＜fr时的模态分析如下。(由于波形的对称性,在此仅取正半周期进行说明)。

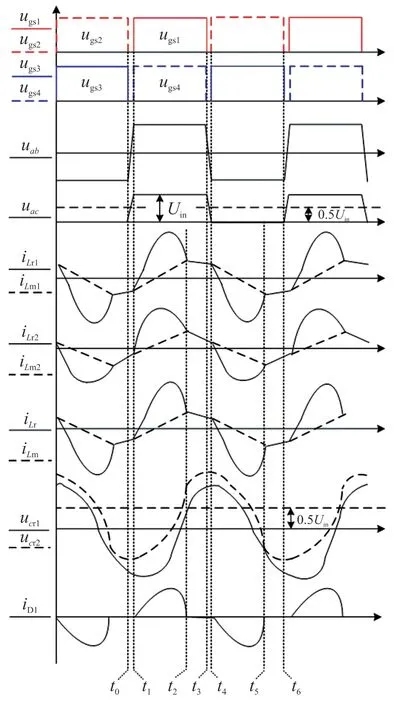
图3 FBDRT LLC 变换器在fs＜frmin时的典型波形

开关模态1[t0～t1]在t0时刻之前,S2、S3两个开关管导通,此时iLr和iLr1为负值,且iLr＝iLm1＋iLm2,变压器原边绕组无电流通过,变压器副边绕组中流过的电流值为0。t0时刻,S1～S4四个开关管全都关闭,此时复合支路总谐振电感电流值为负,即iLr分别给S2、S1的寄生电容分别充放电,同时iLr1给S3的寄生电容充电的时候,给S4的寄生电容放电。当S2寄生电容电压上升到输入电压值时,S1寄生电容的电压下降为0 时,iLr和iLr1分别流过S1、S4的体二极管,为下个模态开关管ZVS 开通创造条件,此时为t1时刻,模态1 结束。模态1 的等效电路图如图2(a)所示。

开关模态2[t1～t2]在t1时刻,打开开关管S1、S4两开关管实现ZVS 开通,副边整流二极管D1和D4开始导通,uab和uac电压都为Uin；两变压器的输出电压之和为Uo,励磁电感Lm1、Lm2被输出电压钳位,谐振电感Lr分别与谐振电容Cr1和Cr2发生串联谐振,输入电压源通过两个谐振支路向负载传输能量,当谐振电感上的电流等于两个励磁电电感上的电流之和时,该模态结束。模态2 的等效电路图如图2(b)所示。

开关模态3[t2～t3]在t2时刻,励磁电感上的电流之和等于谐振电感上的电流,副边电流is自然降到0,D1和D4实现ZCS 关断。此时Lm1、Lm2不再受到输出电压钳位,与谐振电感Lr、谐振电容Cr1一起谐振；t3时刻,开关管S1、S4关断,模态3 结束,变换器进入下半周期的对称模态。模态3 的等效电路图如图2(c)所示。

对[t0～t3]时段内,两个谐振腔列写状态方程:变换器的状态变量分别为iLr、ucr1、

由电感Lr和Lm2在整个开关周期内的伏秒平衡原则可知,uac的直流偏置电压0.5Uin将完全由谐振电容Cr2承担,那么可以得到为

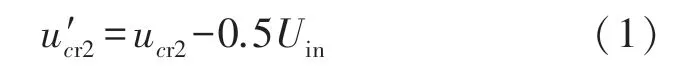
[t0～t1]是原边开关管的死区时间,持续时间很短,可以忽略,那么两个谐振腔的状态变量在时段的[t0～t2]表达式为:

用式(2)加上式(3),便可推导出开关模态1 和开关模态2 时间段内变换器谐振电流iLr和变压器励磁电流iLm的表达式为

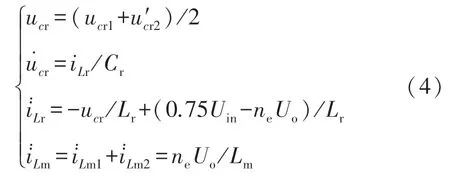
同理,可以得到[t2～t3]时段内iLr和iLm的表达式为

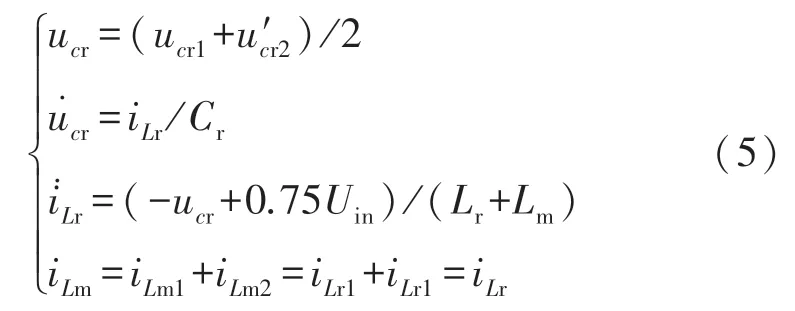
根据以上两个式子,可以将FBDRT LLC 变换器等效成下图的全桥变换器,只是等效的输入电压源变为0.75Uin,如图4 所示。

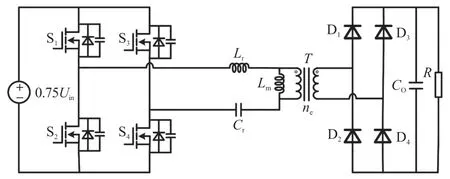
图4 FBDRT LLC 谐振变换器的等效电路

当fs＝fr时,变压器T1的输出电压为±Uin/na,T2的输出电压为±0.5Uin/nb,此时根据变换器的电压增益公式M＝neUo/Uin可以得到M＝0.75。那么FBDRT LLC变换器基于FHA 分析法所得电压增益公式[7]如下:

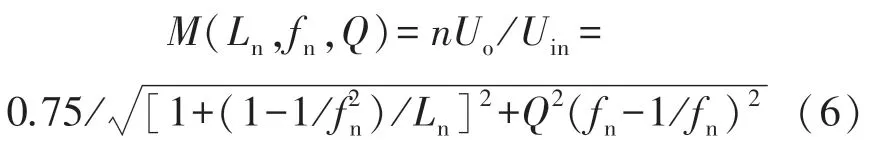
式中:Ln为归一化电感量,Ln＝Lr/Lm；Q为品质因数,Q＝Z0/Req；Req为交流等效电阻,Req＝8n2R/π2；Z0为特征阻抗；fn归一化频率,fn＝fs/fr,fs为开关频率,fr为串联谐振频率。

由式(6)可知,FBDRT LLC 变换器可以降低宽输入电压范围下变换器所需的电压增益需求,它的输入电压变化范围是全桥LLC 变换器的4/3 倍,因此该拓扑更适用于宽输入电压范围下。

1.2 反馈控制回路原理分析

用MATLAB 绘制出电压增益M随电感比(Ln＝Lm/Lr)变化的曲线,如图5 所示。由图5 可知,在归一化频率fn＜1 且品质因数不变的情况下,随着电感比的减小,变换器电压增益曲线越来越陡,变化范围越来越大[8],有利于增大输入电压范围,且变换器工作在定频模式下,有利于减小开关损耗和磁性元件损耗。

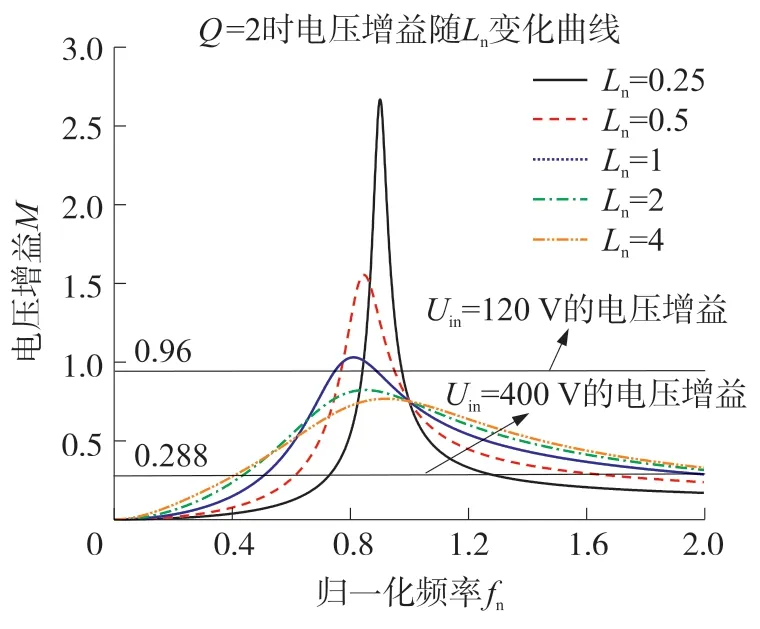
图5 不同Ln 下的电压增益曲线

并且从图中可以看出,使用传统的变频调节方案,当输入电压范围很宽时,变换器需要很宽的频率变换范围,这对变换器中的磁性元件的优化设计是非常不利的,从而导致变换器整体效率降低。因此本文提出一种基于磁控制的可变电感控制方案,让变换器工作在定频模式下,将谐振电感做成可变电感,通过改变电感值,从而改变谐振回路的电压增益,进而调节输出电压。

以宽范围电压为例,为了满足最低输入电压时的最大增益需求,此时需要较小的Ln,即较大的Lr,此时谐振电感Lr上的峰值电流较低,初级开关管的开关损耗较低,有助于提升效率。当输入电压为最大输入电压时,此时对应最小的电压增益,如图所示,Ln较大,即较小的Lr,谐振电感Lr上的峰值电流就会增加,此时初级开关管的导通和关断损耗就会增加,降低变换器的效率,因此在制作可变电感时,电感的最低饱和值应在满足最低电压增益需求的基础上,尽量选取较大的值,以保证峰值电流不会太大,这样就能保证变换器在全电压范围内实现效率的提升。

2 磁控制的可变电感原理简介

可变电感通常采用如图6 所示的双E 型磁芯构成,主要由三个绕组构成,它的主绕组绕制在中间磁柱上,而两个偏置绕组则以相同的匝数分别绕制在磁芯的左右两侧磁柱上。两边磁柱不开气隙,而中间磁柱开气隙(可以防止磁芯快速饱和)。[9-10]可变电感的磁芯结构特性前人已经作出了相应的分析,此处不再赘述。可变电感是通过控制磁芯的饱和程度来控制电感量的变化的,文献[11]对可变电感的感量表达式作出了推导,此处假设边柱磁导率处处相等,记为μv,则感量计算表达式如下:

图6 基于磁控制的可变电感结构图

式中:μv、μc、μ0分别为边柱磁导率,中柱磁导率和中柱气隙的磁导率；lv、lc、lg分别为整个边柱,中柱(不含气隙),气隙的磁路长度；A1,A2,Ae分别为端柱,边柱,中柱的截面积,Ae＝2A1＝2A2,并设A1＝A2＝Av；N为磁芯所绕导线匝数[11]。

由式(7)可知,电感值被划分为前后两个部分,前半部分lv/2μvAviN2中的μv受到反馈控制回路的压控电流源的电流idc的控制；后半部分的lc/μcAeN2＋lg/μ0AeN2是几乎不发生变化的主绕组的电感量[11]。当输出电压发生变化的时候,反馈控制回路通过误差放大器调节压控电流源的电流,从而改变边柱磁导率,达到调节电感的目的。在输入电压为120 V 的时候,标称状态下,此时压控电流源的电流idc为零,没有电流流过控制绕组N1和N2,此时谐振电感具有最大值Lr-max,谐振电感上的电流峰值较低,此时原边开关管的开关损耗就会降低,因此所提方案在低输入标称电压下具有高效率。当压控电流源的电流Idc逐渐增大后,谐振电感值逐渐减小,当Idc增加到一定程度,磁芯完全饱和,此时谐振电感值达到最小值Lr-min。此时无论Idc怎么变化,电感值也不会再发生变化。

3 系统主要参数设计

为验证FBDRT LLC 变换器在宽输入电压[12]时依然能保持高效率,本文设计了输入电压为120 V～400 V、输出为48 V/5 A 的双谐振腔LLC 变换器实验样机。定义Q＝2,fs＝135 kHz。

(1)变压器变比

由上文分析可知,标准输入电压为120 V,并定义二极管和副边线路上压降之和VD＝2 V,因此等效变压器变比可由下式计算为:

(2)谐振槽参数计算

谐振电容Cr的计算公式如下:

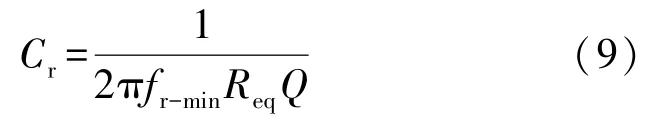
谐振电感Lr的取值范围计算如下:

由上文分析已知,fs＜fr-min,因此在设计时,当可变电感取最大值时,应使串联谐振频率等于开关频率,这样便可以保证开关频率fs在全范围内均小于等于串联谐振频率fr,即变换器工作在ZVS。在标准输入电压下,此时反馈控制回路的压控电流源电流Idc为0,此时谐振电感取最大值,即串联谐振频率取最小值fr-min那么谐振电感最大值计算公式如下:

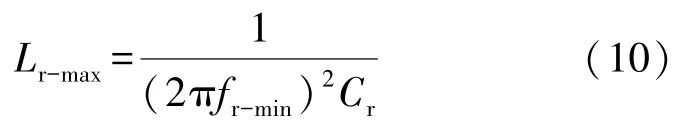
由图5 可以确定最小电感比Ln的值,已知电感比越小,效率越高,但较大谐振电感也会给绕制可变电感的过程增加难度,并且会增大无源器件的体积,折中选择Ln＝1 即可满足电压增益需求。可以求出变压器励磁电感值为

并且由图5 可知,当输入电压为最大值时,电压增益比很小,此时为了避免谐振电感值太小、原边开关管损耗增大而引起效率降低的问题,选择Ln＝4即可满足要求,因此可以求出可变电感最小值为

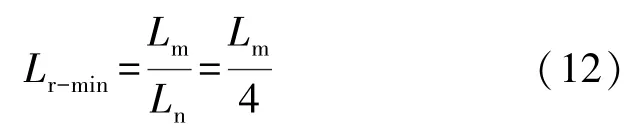
4 实验结果

为了验证以上理论分析的正确性,本文绕制了一个15 μH～60 μH 的可变电感器,制作了一台240 W的实验样机,验证了该变换器在宽输入电压下仍能够安全稳定工作,并且具有高效率。变换器参数如下:

输入电压:120 V～400 V

输出电压:Uo＝48 V

输出电流:Io＝5 A

开关频率:fs＝135 kHz

变压器变比:na＝nb＝3.6

谐振电感:15 μH～60 μH

谐振电容:Cr1＝Cr2＝12 nF

励磁电感:Lm1＝Lm1＝120 μH

图7、图8 为开关管软开关的实现波形。从图7可以看出,在开关管S1开通时,S1的漏源极电压已经下降为0,此时流过开关管电压电流乘积为0,即S1实现ZVS 开通。从图8 可以看出,在t2时刻,流过副边二极管D1的电流已经降为0,即副边二极管实现ZCS 关断。

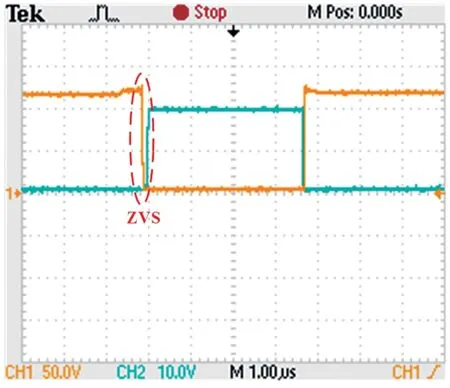
图7 ZVS 实现波形

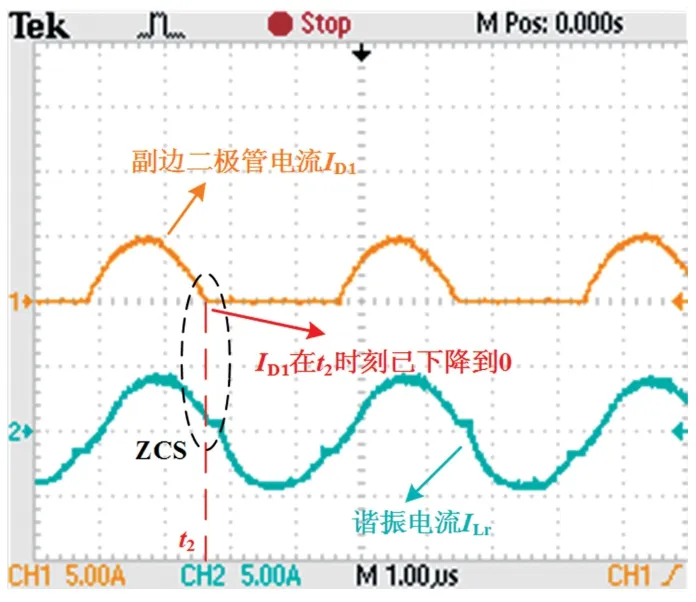
图8 ZCS 实现波形

图9 为变换器的输出电压波形,从图中可以看出,当输入电压发生变化时,变换器通过反馈控制回路控制压控电流源的电流大小,从而可以调节可变电感值,使输出电压稳定在48 V。

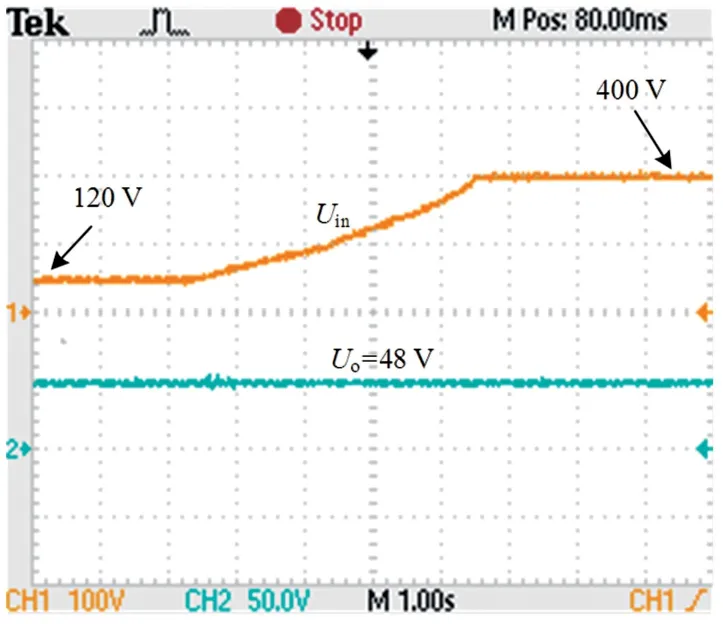
图9 输出电压波形

图10 给出了变换器效率随输入电压的变化曲线,可以看出,FBDRT LLC 变换器的效率随着输入电压的增加而减小,正是由于随着输入电压的增加,可变电感值随之减小,变换器的关断电流和传导电流增加,导致效率η下降。此外,图10 也展示了变换器效率随负载的增加而增加。Uin＝160 V,重载时,η＝90%。

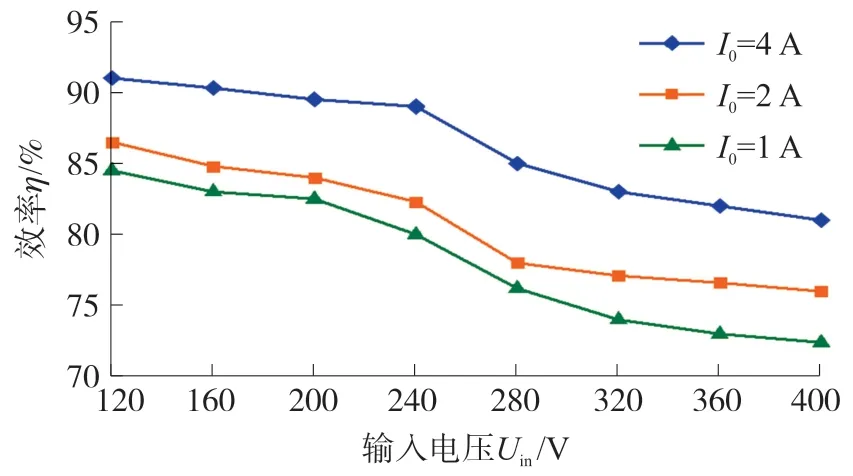
图10 实测变换器的效率曲线

5 结论

本文提出了一种基于磁控制的可变电感器方案来实现稳压的双谐振腔LLC 谐振变换器。通过理论分析和实验验证,得出FBDRT LLC 变换器能够在不牺牲效率的前提下,能够将输入电压变化范围拓宽为全桥LLC 变换器的4/3 倍,能够有效解决目前新能源发电单元受外界环境因素影响的问题。并且所提变换器还具有以下优点:

(1)变换器原边能够实现ZVS,副边能够实现ZCS,开关损耗低,变换效率较高。

(2)该变换器工作在定频模式下,有效解决了变频调控下谐振变换器的EMI 问题,有利于磁性元件的优化与设计,提高了变换器的效率。

(3)变换器原边两条支路的电流互不影响,即变换器的原边不存在环流。