常规凝血试验检验项目测量不确定度和西格玛水平的评定研究

曾露云，王巍，冯紫嫣

(1.北京市西城区妇幼保健院检验科，北京 100054；2.北京金风易通科技有限公司，北京 100102)

检验医学的目标是产生可用于临床决策，改善病人健康的信息，而其基础是需要有足够准确的检查结果[1]。测量不确定度(measurement uncertainty，MU)揭示或给予被测量数值离散性的非负参数，是对测量结果质量的定量表达，不但可以提供准确的测量结果，也能够有效的辅助结果说明，特别是确定同一被测量值在不同测量结果之间是否有差异[2]。MU的应用不但有助于将实验室的检测结果恰当地应用于临床诊断和治疗，还有利于为实验室选择可靠的测量程序并提高实验室服务质量[3]。由外国研究者Nevalainen引用到临床实验室质量管理中的六西格玛(6σ)质量管理[4]，是基于传统质量管理发展起来的方法，能够与不精密度(CV%)、偏倚(Bias%)和允许总误差(TEa)相结合，用于客观、定量地评估检验质量[5]。提高检验质量是医学检验界不变的主题[6]。本研究旨在通过计算常规凝血试验各项目的相对扩展不确定度和σ值，综合评定分析中的检验质量。

1 材料与方法

1.1 材料

采用日本希森美康CS-1300全自动血凝仪及德国西门子配套试剂和校准品，其中质控品包括PT、APTT及Fbg的正常及异常的两个水平。室间质评物由北京市临床检验中心提供。PT、APTT采用凝固法，Fbg采用Clauss法。血凝仪每半年进行一次校准，实验室每日按照仪器说明书保养仪器。室间质评样品的处理严格按照室间质量评价计划的要求执行，校准、室内质控和室间质评样品的测量过程均严格按照实验室常规凝血试验检测项目的标准操作程序(SOP)进行。

1.2 方法

1.2.1 评定方法 (1)评定各项目的测量不确定度：利用实验室2018至2020年常规凝血试验的室间质评数据和实验室2021年常规凝血试验项目的室内质控结果数据，根据中国合格评定国家认可委员会(CNAS)颁布的《医学实验室—测量不确定度的评定与表达》(CNAS-TRL-001:2012)[7]技术报告中“自上而下”的评定方法对实验室常规凝血试验各项目的相对扩展不确定度进行评定，该方法指出，实验室测量不确定度是基于正确度和实验室内测量复现性进行评定的方法。其中，在评定实验室内测量重复性引入的不确定度使用室内质控(IQC)数据，评定偏移引入的测量不确定度使用室间质量评价(EQA)数据。(2)评定各项目的西格玛水平：根据西格玛水平的计算公式σ=(TEa%-|Bias%|)/CV%[5]，计算常规凝血试验项目的σ水平，其中TEa表示允许总误差，按照国家标准GB/T20470-2006临床实验室室间质量评价要求[8]，Bias表示偏倚，CV表示不精密度，分别以百分位数表示。当σ<2时为不可接受水平，当2≤σ<3时为欠佳水平，当3≤σ<4时为临界水平，当4≤σ<5时为良好水平，当5≤σ<6时为优秀水平，当σ>6时为世界一流水平[9]。

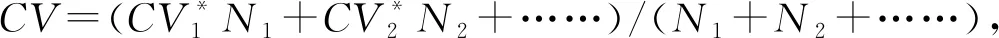
1.2.3 偏倚(Bias%)的计算 (1)计算偏移引入的相对测量不确定度 [ucrel(bias)]分量：使用本实验室参加北京市临床检验中心2018～2020年凝血试验室间质量评价结果数据，共计6次，剔除不可接受数据。(2)计算σ水平：选取实验室参加2021年北京市临检中心凝血试验室间质量评价结果数据。每次EQA活动有5个批号质控品，统计时计算PT、APTT、Fbg以及INR4个凝血试验项目(一年两次)数据的Bias%绝对值的平均值，作为该项目实验室的Bias%估计值。

1.2.4 利用室内质控数据评定实验室内测量复现性引入的相对测量不确定度 收集实验室2021年不同浓度水平不同批次的质控数据，计算不同浓度水平的加权CV，根据公式1评定实验室内测量复现性引入的相对测量不确定度，即实验室内测量复现性引入的相对测量不确定度等于实验室变异系数(CV)。

Urel(Rw)=CV(Rw)=s(Rw)/|x|×100%

(1)

其中，x表示平均值；s(Rw)表示实验室内测量复现性；Urel(Rw)表示实验室内测量复现性引入的相对测量不确定度。

1.2.5 利用EQA数据评定偏移引入的测量不确定度 Nordtest[10]提议以6次PT结果数据作为评定测量不确定度的基础，用以获得一个具有足够可信限的与偏移有关的不确定度分量。为此Nordtest给出了一个新的术语“方法和实验室偏移”，符号为RMSbias。在实际工作中，因为单次PT的公认值很难一致，所以在使用PT数据评定由偏移引入的测量不确定度分量时多采用相对值进行计算,需要的参数包括PT组织者给出的公示值Ccons、每个参加实验室的测量值xi和由所有PT数据分析出的测量复现性SR或RSDR[11]，按以下步骤计算：

(1)根据各实验室实测值和PT组织者给出的公认值，分别按公式(2)、公式(3)计算一次PT的偏移量值和相对偏移量值：

bi=xi-Ccons,i

(2)

(3)

式中，bi表示单次PT的偏移量值；xi表示各实验室单次PT的测量值；Ccons,i表示一次PT的公认值；brel,i表示一次PT的相对偏移量值。

(2)按公式(4)、公式(5)分别计算方法和实验室偏移和相对偏移：

(4)

(5)

式中，RMSbias表示方法和实验室偏移；bi表示单次PT的偏移量值；n表示PT次数；RMSrel(bias)表示相对的方法和实验室偏移；brel,i表示一次PT的相对偏移量值。在实际工作中，通常根据根据公式5采用相对值进行计算[10]。

(3)按公式(6)计算单次PT公认值的测量复现性引入的相对测量不确定度：

(6)

式中，urel(cons,i)表示单次PT公认值的测量复现性引入的相对测量不确定度；RSDR,i表示单次PT的相对测量复现性；m表示参加单次PT的实验室数量。

(4)按公式(7)计算多次PT公认值的测量复现性引入的相对测量不确定度：

(7)

式中，urel(Cref)表示多次PT公认值的测量复现性引入的相对测量不确定度。可将此值看成类似分析CRM(CRM)[7]方法评定偏移引入的测量不确定度中的重复测量标准物质的测量不确定度urel(CRM)，以符号urel(Cref)表示。urel(cons,i)表示单次PT公认值的测量复现性引入的相对测量不确定度；n表示PT次数。

(5)按公式(8)计算偏移引入的相对测量不确定度：

(8)

式中，ucrel(bias)表示偏移引入的相对测量不确定度；RMSrel(bias)表示相对的方法和实验室偏移；urel(Cref)表示多次PT公认值引入的相对测量不确定度。

1.2.6 评定相对合成标准不确定度(ucrel) 采用自上而下的方法，只考虑评定检测过程的不确定度，不考虑检测前和检测后阶段各种组分对测量不确定度的贡献，按公式(9)进行计算：

(9)

1.2.7 评定相对扩展不确定度(Urel) 按公式(10)计算：

Urel=k×ucrel

(10)

式中，Urel表示相对扩展不确定度；k表示包含因子。对于正态分布，k=2时，包含概率p=95.45%；k=3，包含概率p=99.73%；通常采用采用k=2；ucrel表示合成相对标准不确定度。

1.2.8 计算各项目的质量目标指数(QGI) 质量目标指数是对实验室方法的偏倚(Bias%)和不精密度(CV%)的评价[12]，根据其计算公式QGI=Bias(%)/(1.5×CV)计算实验室σ<6的常规凝血试验检测项目的质量目标指数，当QGI<0.8时，说明该检测项目需要优先改进的为精密度[13]；当QGI>1.2时，提示该检测项目需要优先改进的为准确度；当0.8≤QGI≤1.2时，说明该检测项目需同时改进准确度和精密度[14]。

2 结果

2.1 实验室内测量重复性引入的相对测量不确定度

实验室2021年常规凝血试验质控品未更换过批号，统计本室本年度常规凝血试验不同浓度的室内质控数据，检验试剂更换批号后完成校准且样本平行比对测试结果合格后，方可使用新批号试剂。检验过程由经过培训考核授予上岗的不同检验技术人员操作。根据公式1得出实验室内测量重复性引入的相对测量不确定度。见表1。

表1 不同浓度水平常规凝血试验项目室内测量重复性的相对测量不确定度

2.2 偏移引入的相对测量不确定度

统计2018年至2020年的6次EQA结果，记录与室内质控品浓度水平相近的EQA样本的偏移，根据公式5计算RMSrel(bias)，再根据公式(7)和公式(8)分别计算urel(Cref)和ucrel(bias)。见表2。

表2 偏倚引入的相对测量不确定度

2.3 凝血试验各项目的相对合成不确定度和相对扩展不确定度

最后把以上不确定度分量进行合成，根据公式(9)和公式(10)，计算实验室常规凝血试验各项目的相对合成不确定度和相对扩展不确定度。见表3。

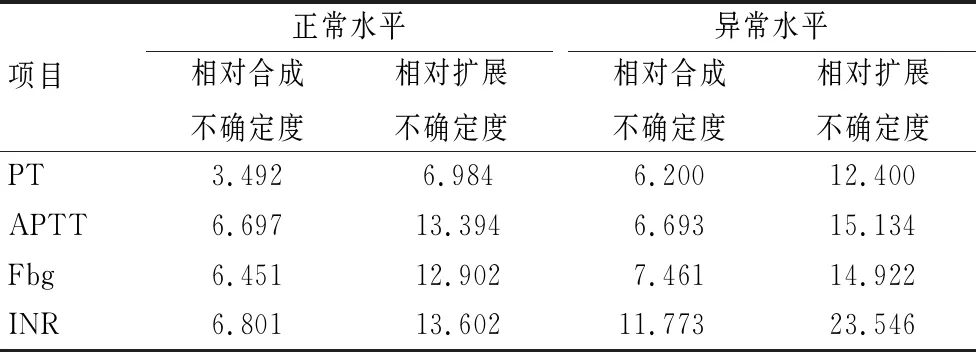
表3 凝血试验项目的相对合成不确定度和相对扩展不确定度

2.4 凝血试验各项目的性能水平及质量目标指数

以国家标准[8]的允许总误差评估实验室常规凝血试验检测项目的性能水平，结果显示PT和INR的σ<3，处于欠佳水平；APTT和Fbg的σ>3，处于临界水平。同时计算本室凝血试验各检测项目的质量目标指数，除APTT的QGI在0.8～1.2以外，其余各项目的QGI均小于0.8。见表4。

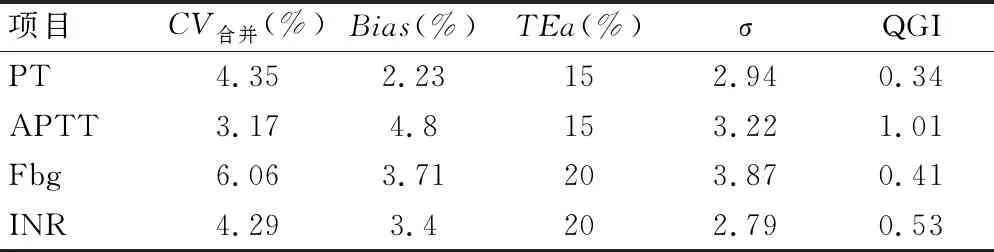
表4 凝血试验项目的性能水平和质量目标指数

3 讨论

随着人类对检测质量的不断探索，测量不确定度在20世纪60年代被引入。Infusino等[15-16]的研究证明了测量不确定度的评定一方面对于验证体外诊断产品(IVD)的质量至关重要，另一方面对于提高临床实验室的检测质量和正确解释结果也具有重要的作用。用于医学实验室的国际标准主要有ISO/IEC 17025《检测和校准实验室能力的通用要求》和ISO 15189《医学实验室质量和能力的专用要求》；国内标准主要包括中国合格评定国家认可委员会(CNAS)颁布的CNAS-CL01《检测和校准实验室能力认可准则》和CNAS-CL02《医学实验室质量和能力认可准则》，上述标准都提出了评定实验室测量不确定度的要求。

目前可用于医学实验室测量不确定度的评定方法主要有1993年由计量学指南联合委员会颁布的《测量不确定度的表达指南》(GUM)提出的自下而上的方法与2003年由Magnusson等提出的自上而下[10]两种方法，“自下而上”法是基于对测量的全面分析后，判別出各种可能的不确定度来源，主要使用在执行参考测量程序的认证实验室和参考物质赋值中的不确定度评定，常规临床实验室运用较少。而自上而下的评定方法，是在控制不确定度来源或程序的条件下，利用统计学原理直接评定特定测量系统内受控结果的测量不确定度[7]。国外研究结果显示，一般情况下，如果临床医学实验室测量不确定度的评定是正确的，两种方法的评定结果应十分接近并可互换[17]。

中国合格评定国家认可委员会(CNAS)推荐的“自上而下”法比较适用于一般实验室，并于2012年颁布相应技术报告《医学实验室—测量不确定度的评定与表达》[7]。本研究即根据该技术报告利用自上而下法评定与本实验室常规凝血试验检测过程有关的检验结果的不确定度。将《临床实验室室间质量评价要求》中的总误差设定为目标不确定度，结果发现本实验室INR和APTT在异常水平(3.74和48.96 s)附近时检验中的相对扩展测量不确定度(23.55%和15.13%)高于目标不确定度(20%和15%)外，其余结果均满足目标不确定度的评价要求。实验室在未来的工作中还需通过自下而上的方法来识別不确定度的各种来源，改进主要影响因子，从而降低测量不确定度。

基于以上结果，本小组又对本实验室常规凝血试验的检验中阶段，通过测量变异的方法利用公式计算评价实验室检测中的西格玛(σ)性能水平[18]。西格玛作为希腊字母“σ”的音译词，是统计学里的一个单位，也是一种评价生产过程和产品特性波动大小的统计量，其高低能够反映质量水准的好坏[19]。研究结果显示本室常规凝血试验检测项目中APTT和Fbg处于临界水平；PT和INR处于欠佳水平，均小于6σ水平。根据6σ管理要求，对达不到6σ水平的项目还需进行质量目标指数(QGI)的计算[12]，结果显示，除APTT的QGI为0.8～1.2外，其余各项目的QGI均<0.8。提示PT、INR和Fbg需要优先改进精密度；APTT既需要改进紧密度又需要改进正确度。由此可见，对于本实验室常规凝血试验而言，提高检测中的精密度是首要任务。

综上，本实验室应根据常规凝血试验检测项目的西格玛水平和质量目标指数，详细评估导致实验室常规凝血试验各项目的检测性能未能达到6σ水平的可能原因，从而更好地控制医学实验室中测量不确定度的来源，在保证不确定度来源和程序可控的条件下，重新评定这些项目的相对扩展测量不确定度。结合测量不确定度和σ的优势，全面分析实验室检验中的质量水准[20]，有助于实验室质量持续改进。