Evaluation of Arctic sea ice simulation of CMIP6 models from China

LI Jiaqi, WANG Xiaochun, WANG Ziqi, ZHAO Liqing & WANG Jin

Evaluation of Arctic sea ice simulation of CMIP6 models from China

LI Jiaqi, WANG Xiaochun*, WANG Ziqi, ZHAO Liqing & WANG Jin

School of Marine Sciences, Nanjing University of Information Science and Technology, Nanjing 210014, China

Nine coupled climate models from China participating in the Coupled Model Intercomparison Project Phase 6 (CMIP6) were evaluated in terms of their capability in ensemble historical Arctic sea ice simulation in the context of 56 CMIP6 models. We evaluated these nine models using satellite observations from 1980 to 2014. This evaluation was conducted comprehensively using 12 metrics covering different aspects of the seasonal cycle and long-term trend of sea ice extent (SIE) and sea ice concentration (SIC). The nine Chinese models tended to overestimate SIE, especially in March, and underestimate its long-term decline trend. There was less spread in model skill in reproducing the spatial pattern of March SIC than in reproducing the spatial pattern of September SIC. The error of March SIC simulation was distributed at the margins of sea ice cover, such as in the Nordic Seas, the Barents Sea, the Labrador Sea, the Bering Sea, and the Sea of Okhotsk. However, the error of September SIC was distributed both at the margins of sea ice cover and in the central part of the Arctic Basin. Five of these nine models had capabilities comparable with the majority of the CMIP6 models in reproducing the seasonal cycle and long-term trend of Arctic sea ice.

coupled climate model, CMIP6, Arctic sea ice

1 Introduction

Coupled climate model is the main tool used to study the evolution of sea ice and its potential impact on the Earth’s climate. The World Climate Research Program is implementing the Coupled Model Intercomparison Project Phase 6 (CMIP6) (Eyring et al., 2016; Zhou et al., 2019). Each phase of CMIP contains dozens of climate models from multiple countries, and their simulations form the basis of the Intergovernmental Panel on Climate Change assessment report. However, studies have found that these climate models still have significant uncertainties in simulating sea ice variability (Stroeve et al., 2012; Notz et al., 2020; Shu et al., 2020; Long et al., 2021; Shen et al., 2021; Watts et al., 2021).

Sea ice extent (SIE) is the total area where the sea ice concentration (SIC) is greater than 15%, and expresses the integral of Arctic sea ice distribution. Shu et al. (2020) compared the multi-model ensemble mean of SIE of 44 models in CMIP6 with observations and the CMIP5 results. The CMIP6 ensemble mean can reproduce the seasonal cycle of Arctic SIE. Compared with the CMIP5 models, the differences among the CMIP6 models were smaller. However, the CMIP6 models failed to reproduce the accelerated decline trend of Arctic summer sea ice since 2000.

Although SIE provides a good general description of sea ice distribution, in reality, the formation, melting, and drift of sea ice have notable regional differences. Therefore, the spatial distribution of Arctic sea ice is also an important consideration when evaluating model simulation skill for Arctic sea ice. Qiu et al. (2015) evaluated the Arctic SIC of the CMIP5 multi-model mean, but did not discuss the differences among the models. Shen et al. (2021) evaluated the capability of 36 models participating in CMIP6 and their 24 CMIP5 counterparts in simulating the mean state and variability of Arctic sea ice cover for the period 1979–2014. A performance score was developed that can be used to form a weighted average for future projections. Their evaluation mainly focused on the CMIP6 ensemble mean results, not on each individual model. In the 36 models evaluated, six models from China were included. Long et al. (2021) evaluated 35 CMIP6 models using metrics for different aspects of Arctic sea ice. They pointed out the performance differences among models with different spatial resolutions. Among the 35 models analyzed, four models were from China. Watts et al. (2021) evaluated a subset of CMIP6 models, with metrics developed specifically for ice edges, and postulated that the model errors in certain regions may be linked to oceanic processes. In the models they analyzed, only one model was from China. Numerous studies have evaluated the CMIP6 models in terms of multi-model means with regard to spatial distribution and temporal evolution, but only a limited number of studies have focused on each individual model (Notz et al., 2020; Shu et al., 2020).

As one of the major countries participating in CMIP6, China contributes a total of nine models from six research institutions. The differences among models from China and their common shortcomings are worth exploring. The evaluation of Arctic sea ice in Chinese climate models is not only important for understanding current and future sea ice changes, but also helpful for improving these models. Research work along this direction may be useful to plan and coordinate model development and evaluation among climate modeling groups in China. The present research focused on these nine models in terms of spatial patterns and temporal variations of Arctic sea ice. We also compared these nine models with 56 CMIP6 models in general. The objective of our research is to provide a comprehensive and detailed evaluation of these nine models, in terms of their skills in reproducing different aspects of Arctic sea ice variability.

This paper is organized as follows. After the introduction, the data and methods are presented in section 2. The evaluation of Arctic sea ice simulation in terms of seasonal cycle, long-term trend, and spatial distribution is presented in section 3. Section 4 provides a summary and conclusions.

2 Data and methods

2.1 Model SIC output and satellite observations

There are currently 56 models that have submitted their outputs to CMIP6. Nine of these models are from China: BCC-CSM2-MR (Wu et al., 2019) and BCC- ESM1-0 (Wu et al., 2020) from the Beijing Climate Center; CAMS-CSM1-0 (Rong et al., 2018, 2019) from the Chinese Academy of Meteorological Sciences (CAMS); CAS- ESM2-0 (Zhou et al., 2020), FGOALS-f3-L (He et al., 2019, 2020), and FGOALS-g3 (Tang et al., 2019) from the Institute of Atmospheric Physics, Chinese Academy of Sciences; CIESM (Lin et al., 2019) from Tsinghua University; FIO-ESM-2-0 (Song et al., 2019) from the First Institute of Oceanography (FIO), Ministry of Natural Resources; and NESM3 (Cao et al., 2018, 2019) from Nanjing University of Information Science and Technology (NUIST). Details of these nine models are presented in Table 1. The sea ice components in three of the nine coupled climate models are represented by the Sea Ice Simulator (SIS) model (Winton, 2000), whereas the sea ice components of the other six models are represented by version 4 of the Los Alamos sea ice model (CICE) (Hunke et al., 2020). The spatial resolution of all nine models is about 1° (Table 1).

Table 1 Sea ice model information of nine coupled models from China in CMIP6

Monthly SIC outputs of CMIP6 historical runs were used in this study. To reduce the influence of internal variability on our results, the model outputs used were the ensemble means, obtained from the member outputs submitted by each model to CMIP6. To date, the number of members from these nine models has varied from three to six (last column in Table 1). In CMIP6, historical simulation refers to simulation since 1850 driven by various external forcing fields based on observations to evaluate the capability of models to reproduce climate variability from 1850 to 2014. In this study, the model SIC fields from 1980 to 2014 were compared with observations.

The observational data were the satellite remote sensing product G02202 (Meier et al., 2017) from the National Snow and Ice Data Center (NSIDC). This data set contains SIC obtained by two inversion algorithms and SIC obtained by combining these two algorithms based on the National Oceanic and Atmospheric Administration (NOAA) Climate Data Record (CDR). The two inversion algorithms are the National Aeronautics and Space Administration (NASA) Team inversion algorithm and Bootstrap inversion algorithm. The spatial resolution of satellite SIC observation is 0.25º×0.25º. Because the models had different spatial resolutions from that of the observations and among the models, all the data were interpolated bilinearly to a 1º×1º grid. For the SIE computation, the SIC from the model grid was first interpolated to a 1º×1º grid, and the 15% criterion was then used.

2.2 Evaluation method of spatial distribution of SIC

To evaluate the performance of these nine models in the simulation of Arctic SIE, we calculated SIE as the sum of the areas of all grid points with SIC greater than 15% and north of 30.98ºN, which is consistent with the definition used by the NSIDC and other researchers. The evaluation of SIE was focused on its seasonal cycle and long-term trend. The seasonal cycle of SIE was determined based on the multi-year average of SIC from 1980 to 2014. The long-term trend of SIE was obtained from a linear fit of SIE from 1980 to 2014. The present research also compared the standard deviations after removing a linear trend and the annual range of SIE, the difference of maximum and minimum SIE. The standard deviation after the linear trend is removed represents the fluctuations of Arctic sea ice. The annual range is the difference between the mean SIEs in March and September.

The spatial distribution of sea ice was also evaluated in terms of SIC and its long-term trends in March and September. In particular, the spatial distribution of SIC refers to the average SIC from 1980 to 2014. The long-term trend of SIC is the linear trend from 1980 to 2014 that is significant at the 95% level. To quantify the skill of a model in simulating the distribution and long-term trend of SIC, the Taylor score (TS) index proposed by Taylor (2001) was used,

To show the common spatial characteristics of model errors, the statistic D, the multi-model root mean square error (RMSE), was used,

2.3 Metrics for evaluation

To comprehensively assess the capability of the models in simulating Arctic sea ice, a method developed by Huang et al. (2017) and Long et al. (2021) was used. In this method,metrics are chosen to comprehensively evaluate the capability of each model. First, for the observation of thethmetricB,Sis defined as

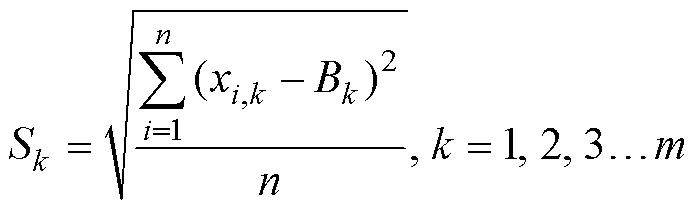
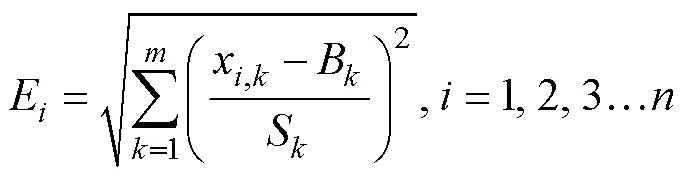
which combines the skill of the model in reproducing allmetrics in a non-dimensional manner. According to formulae (3) and (4), the-score represents the comprehensive skill in reproducing the observedmetrics. A smaller-score is associated with better model simulation capability.

When the-score is computed for allmodels andmetrics, the absolute value of the term inside the square root of formula (4),

can be used to measure the skill of theth model in reproducing theth metric and analyze its contribution to the comprehensive skill of the model, the-score.Twelve metrics were used in our analysis, which are listed in Table 2 with their respective values for the nine Chinese models. For the metrics associated with SIE, the March SIE and its standard deviation, September SIE and its standard deviation, long-term trend of March SIE, long-term trend of September SIE, annual long-term trend of SIE, and range of SIE, a single value is given for each metric. For metrics associated with the comparison of two-dimensional fields, March SIC, September SIC, and their long-term trends, the TS index as defined in formula (1) was used as a metric.

Table 2 Sea ice metrics from observation and nine model simulations

Notes: The italic and bold numbers mean that the result is not significant at 95% level; Taylor Score (TS) indices are calculated following formula 2.

3 Results

3.1 Seasonal cycle of Arctic SIE

For the nine coupled climate models listed in Table 1, we evaluated their capabilities to simulate the seasonal cycle of Arctic SIE (Figure 1). Figure 1 indicates that the observed Arctic SIE increased to its maximum in March and then decreased to its minimum in September. Eight out of the nine models could capture the timing of the observed seasonal cycle of Arctic SIE, but the ninth model, NESM3, reached its Arctic SIE maximum in April instead of March. Based on the SIE observation from 1980 to 2014 (Table 2), the average March SIE was 15.55×106km2, with a standard deviation of 0.47×106km2. One model yielded March SIE within the range of the observed SIE plus and minus one standard deviation of observed SIE; that is, [16.02, 15.08]×106km2. Seven of the nine models overestimated March SIE. For September, the range of observed average SIE plus and minus one standard deviation was [7.45, 5.29]×106km2. The results of three of the nine models were within this range. Four of the nine models overestimated September SIE and two models underestimated it; CIESM severely underestimated September SIE because of abnormally high shortwave radiation at high latitudes (Lin et al., 2020). The March SIE result of CAS-ESM2-0 was the most similar one to the observations. The September SIE result of NESM3 was the most similar one to the observations. Compared with the observations, CIESM results underestimated Arctic SIE for all months.

To gain insight into the skills of these nine models in simulating the seasonal cycle of SIE, we compared them with the CMIP6 models. The gray shaded area in Figure 1 represents the multi-model means (MMMs) and their standard deviations (STDs) of the 56 CMIP6 climate models. The shaded upper and lower limits of each month indicate MMM + STD and MMM − STD, respectively. The MMMs could reproduce the observed seasonal cycle of SIE very well, which is a major improvement of the CMIP6 models compared with the CMIP5 models (e.g., Notz et al., 2020; Shu et al., 2020). The SIEs for two of the nine models were distributed in the MMM ± STD range in March. Two SIEs were distributed in the MMM ± STD range for September. Compared with the CMIP6 models in general, the nine Chinese models tended to overestimate SIE, especially in March.

Table 2 presents the mean and seasonal extreme values of SIE during 1980–2014 for the nine Chinese models. The mean value represents the total Arctic SIE, and the extreme values in March and September are represented by the amplitude of the seasonal SIE cycle. As shown in Table 2, the mean values of SIE simulated by FIO-ESM-2-0 and CAS-ESM2-0 were more similar to the observations than were the mean SIEs of the other models. Among the nine models, eight models overestimate the maximum values of SIE; five models overestimate the minimum values of SIE. Three models underestimated the minimum values of SIE, and the minimum SIE value of NESM3 was similar to the observed value. For the seasonal cycle amplitude, the best simulations were produced by BCC-CSM2-MR and BCC-ESM1-0.

Figure 1 The mean seasonal cycle of sea ice extent for 1980–2014. The grey shaded region is the multi-model ensemble mean from 56 CMIP6 models plus and minus its standard deviation.

3.2 Long-term trends in SIE

The long-term trends of SIE simulated by the nine Chinese models are also presented in Table 2, along with their observational counterparts. For the observed long-term trend of March SIE, the 95% significant interval was [–4.69, –2.88]×104km2·a–1. Four of the nine models showed declining trends within this interval. For the long-term trend of September SIE, the 95% significant interval was [–10.96, –7.10]×104km2·a–1based on observations. Three of the nine models indicated declining trends within this interval. Five of the nine models underestimated the declining September SIE trend. The 95% significance interval of the annual long-term trend of SIE was [–6.29, –5.55]×104km2·a–1. Only one model showed a declining SIE trend within this interval. Seven of the nine models underestimated the annual trend. For the declining trend of September SIE, the result of BCC-CSM2-MR was the most similar one to the observation. Thus, these nine models tended to overestimate SIE, especially for March, and underestimate the long-term declining trend of SIE, especially for September.

3.3 Spatial distribution of SIC

To analyze the spatial distribution of sea ice simulation, SIC was evaluated for the nine models. Figure 2 shows the observed Arctic SIC in March, the multi-model means from the 56 CMIP6 models and nine Chinese models, and the multi-model RMSE for the 56 models and nine Chinese models based on formula (2). Satellite observations captured in March showed that the entire Arctic Basin was covered by SIC above 95%, and that the SIC gradually decreased from high latitudes to low latitudes at the margins of sea ice cover. The common errors of the nine Chinese models and 56 CMIP6 models were mainly distributed at the margins of sea ice cover, such as in the Nordic Seas, the Barents Sea, the Labrador Sea, the Sea of Okhotsk, and south of the Bering Strait. The models tended to overestimate SIC in these regions. The overestimation was greatest in the Nordic Seas and Barents Sea, followed by the Sea of Okhotsk and the Labrador Sea. Compared with the 56 CMIP6 models, the nine models from China produced greater overestimation of SIC in the Nordic Sea, the Barents Sea, and the Sea of Okhotsk (Figures 2b, 2c). The multi-model RMSEs for the 56 models and the nine Chinese models reflect these results.

Figure 3 shows the bias of the 1980–2014 mean March SIC between the nine models from China and the observed SIC. All nine models could simulate the March SIC in the Arctic Basin reasonably well, but the performance of each model varied for the margins of sea ice cover. Observations indicated that Arctic sea ice could extend to the western part of the Sea of Okhotsk in March. BCC-CSM2-MR, BCC-ESM1-0, CAMS-CSM1-0, CAS-ESM2-0, FGOALS- g3, and NEMS3 overestimated SIC in this region, whereas CIESM and FGOALS-f3-L underestimated SIC in this region. In the Nordic Seas and the Barents Sea, sea ice covered only the northern parts in March and extended southward in the Labrador Sea and along the coast of northern Europe (Figure 2a). FIO-ESM2-0 and CIESM simulations of this region were relatively similar to the observations. The other seven models overestimated SIC in the Nordic Seas and the Barents Sea. For the coastal region of the Labrador Sea, the simulations of BCC-CSM2-MR, BCC-ESM1-0, and FIO-ESM-2-0 of the SIC in this region were more similar to the observations than were those of the other models, although they resulted in some underestimation. CAMS-CSM1-0, FGOALS-f3-L, and NESM3 overestimated SIC in this region.

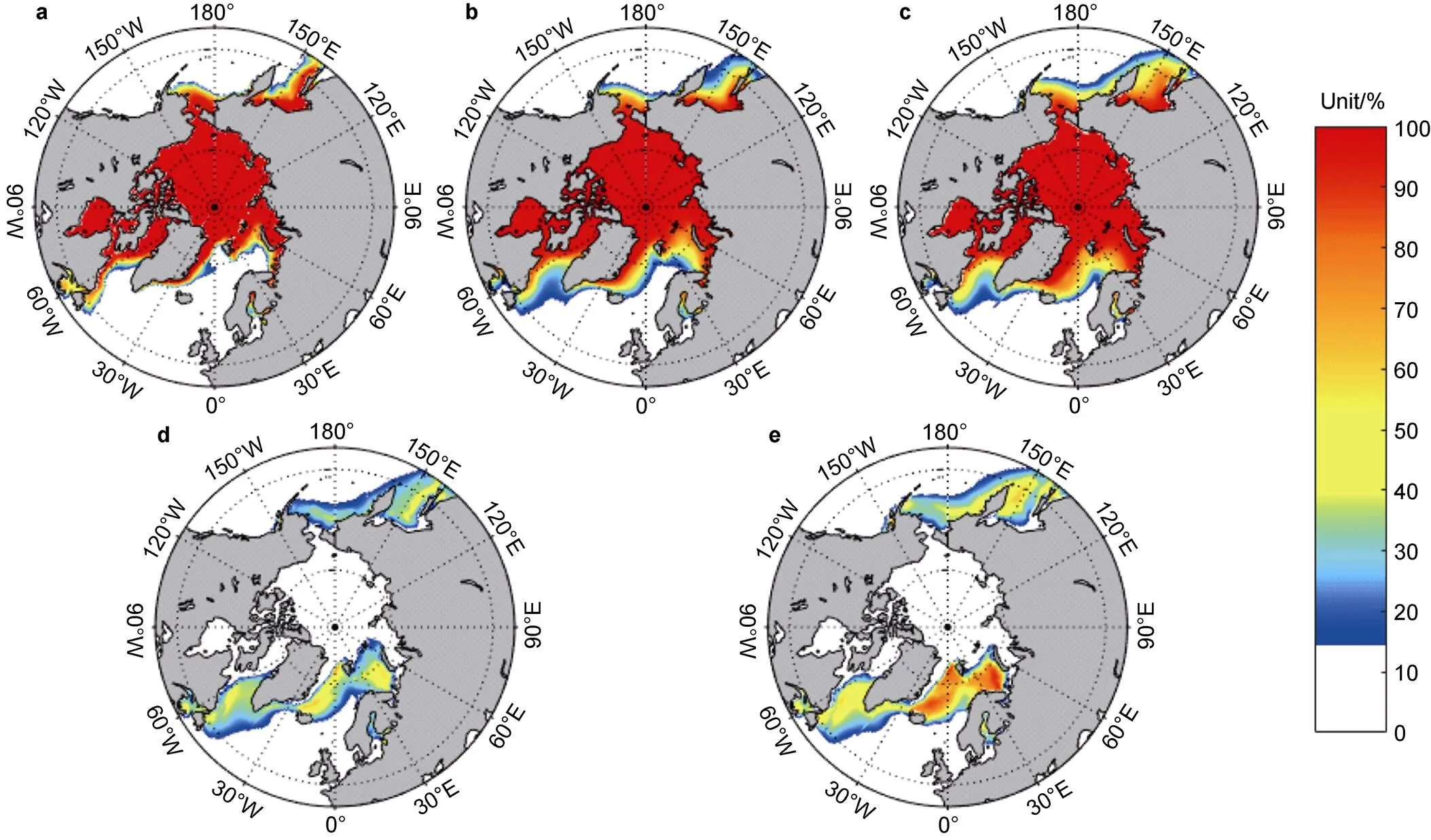
Figure 2 Spatial distribution of 1980–2014 March mean SIC from observation (a), 56 CMIP6 models (b), 9 Chinese models (c), root mean square error of 56 models (d), and root mean square error of 9 Chinese models calculated by formula (2) (e).

It is worth noting that in the counterpart model version participating in CMIP5, FIO-ESM overestimated the SIC on the east coast of North America (Figure 3 of Shu et al., 2013). Similarly, in the version participating in CMIP5, FGOALS-g2 underestimated the SIC in the same area in March (Figure 1 of Xu et al., 2013). In this aspect, for the model versions participating in CMIP6, the simulations of these two models were improved compared with their respective versions participating in CMIP5.

Table 2 presents the TS indices of the nine Chinese models in reproducing the spatial features of March SIC. Of the nine models, FIO-EMS-2-0 had the highest TS index, indicating that this model could best reproduce the spatial features of the observed SIC in terms of the spatial correlation and spatial variance of SIC, as shown in formula (1).

The observed SIC in September showed that the sea ice edge retreated to around 75°N because of sea ice melting (Figure 4a). Compared with the simulation results for March, there was a considerable difference between the model results in September and the observations. Both the 56 CMIP6 models and the nine Chinese models had SIC error in the Arctic Basin and the margin of sea ice cover. In addition to the large error in the margin of sea ice cover, there was also SIC error of about 20%–40% in the Arctic Basin. The RMSE from the nine Chinese models was larger than that of the 56 CMIP6 models in the central Arctic region. Compared with the 56 CMIP6 models, the nine Chinese models tended to more severely underestimate SIC in this region.

In contrast to the results for March, the modeled September SIC had biases in both the margin of sea ice cover and the central Arctic Basin (Figure 5). Among the nine models, CAMS-CSM1-0 could best simulate the spatial distribution of SIC in September with the highest TS index, as shown in Table 2. For the Nordic Seas and the Barents Sea, BCC-CSM2-MR, BCC-ESM1-0, and FGOALS-g3 overestimated SIC in this region. For the central Arctic Basin, BCC-CSM2-MR, BCC-ESM1-0, CAMS-CSM1-0, and FGOALS-g3 accurately simulated SIC. However, CAS-ESM2-0, CIESM, and FIO-ESM-2-0 underestimated SIC for this region, and CIESM had the most negative bias. It is worth noting that in the version participating in CMIP5, BCC-CSM2-MR overestimated SIC off of northwestern Greenland in September (Figure 1 of Wang et al., 2020). In the version participating in CMIP6, the simulation of this model was improved in this aspect.

Figure 3 The bias of 1980–2014 mean March SIC of nine models from China (model minus observation).

In the CIESM simulation, only a very small amount of sea ice was present in the Arctic Ocean in September (Figure 5). Lin et al. (2020) showed that the summer SIEs of CIESM in both the Northern and Southern hemispheres were abnormally low, and that the summer SIE of the Arctic was less than 1.0 × 106km2. In this model, poleward of 60°, the absorbed shortwave radiation was abnormally high by 50 W·m−2, and the temperature from 1000 hPa to 700 hPa was abnormally high by 5℃. The specific reasons for this deviation (such as sea ice albedo feedback and the effects of clouds) are still under investigation (Lin et al., 2020).

According to the TS indices listed in Table 2, the skill of these nine models in reproducing March SIC was comparable, whereas the skill in reproducing September SIC varied greatly. The standard deviation of the TS indices for March SIC was 0.11, varying from 0.47 to 0.81. In contrast, the standard deviation for September SIC was 0.28, varying from 0.00 to 0.87. The difference of the standard deviations for March and September SIC was significant at the 95% level based on the-test, which indicates that it was more difficult to reproduce the spatial features of September SIC.

3.4 Spatial distribution of long-term trends in SIC

Figure 6 shows the observed long-term trend of SIC in March, the multi-model mean trend from the 56 models and nine Chinese models, and the multi-model RMSE based on formula (2). Observations showed that the decline in March SIC was not widespread. The SIC decline trend was around 2% per year in the Barents Sea, where the decline was relatively rapid. The spatial distribution of the decline trend of SIC showed that the rate of decrease of sea ice cover in the margin region was higher than that in the central part of the Arctic Basin. Overall, the models overestimated the area of sea ice decline. The regions of large model errors were in the Sea of Okhotsk, the Barents Sea, and south of Greenland. Compared with the 56 CMIP6 models, the nine Chinese models tended to overestimate the sea ice trend and produce larger errors in the Nordic Seas, the Barents Sea, and the Labrador Sea.

The nine models from China had various skill levels in reproducing the trend of SIC in March (Figure 7). Notably, the observations showed regions with a small increasing trend in SIC near the Bering Strait, which was also shown in a detailed analysis of sea ice area trends by Peng and Meier (2018). However, none of the models were capable of simulating this feature. CIESM and FIO-ESM-2-0 simulated the decline of SIC in the Sea of Okhotsk, whereas BCC-ESM1-0, CAS-ESM2-0, and FGOALS-g3 simulated the decline of SIC at lower latitudes. The reason is that the latter three models overestimated the SIC in the region, shifting the sea ice margin southward, and thus also shifting the SIC decline region southward. According to the observations, there was a band of decline in SIC extending from the Barents Sea to the east coast of Greenland. NESM3 could simulate this feature, but overestimated the decline trend. FIO-ESM-2-0 had the highest TS index in reproducing the March SIC trend (Table 2).

Figure 4 Spatial distribution of 1980–2014 September mean SIC from observation (a), 56 CMIP6 models (b), 9 Chinese models (c), root mean square error of 56 models (d), and root mean square error of 9 Chinese models calculated by formula (2) (e).

Figure 5 The bias of 1980–2014 mean September SIC of nine models from China (model minus observation).

Figure 6 Spatial distribution of 1980–2014 linear trend of Arctic SIC in March from observation (a), 56 models (b), 9 Chinese models (c), root mean square error of linear trend of 56 models (d), and root mean square error of linear trend of 9 Chinese models calculated by formula (2) (e). The color bar for (a), (b), and (c) is shown vertically on the right and the color bar for (d) and (e) is shown horizontally on the bottom.

It was more challenging to reproduce the decline trend in September SIC in these models (Figure 8). According to the observations, the decline of Arctic sea ice was more notable in September, and the region characterized by the strongest decline trend was located at the margin of sea ice cover. However, compared with the observations, there were large discrepancies in the modeled margins of sea ice cover, and therefore in the region of the decline trend.

Figure 9 shows the spatial distribution of the long-term trend of SIC in September for the nine Chinese models. The observed decline trend of SIC in September was mainly distributed in a circular region extending westward from the Beaufort Sea to the Laptev Sea and Kara Sea (Figure 8a), which also represented the sea ice margin in September (Figure 4a). BCC-CSM2-MR simulated the spatial characteristics of the decline area of SIC, but the magnitude of the decline was underestimated, and SIC decline also appeared in the Barents Sea region. The reason may be that the BCC-CSM2-MR simulation showed sea ice in the Barents Sea in September (Figure 5), whereas no sea ice occurred in this region in the September observations (Figure 4). In the simulations of CAS-ESM2-0 and FIO-ESM-2-0, the area of SIC decline shifted to the central part of the Arctic Basin. Because the area of SIC decline is related to the distribution of SIC to a certain extent, such errors may be related to the fact that the two models underestimated the extent of sea ice in September, and that the distribution of sea ice shifted to the central part of the Arctic Basin (Figure 5). NESM3 could simulate the rapid decline of SIC from the Beaufort Sea to the Kara Sea reasonably well, and also had the highest TS index in reproducing the September SIC trend (Table 2).

From Table 2, it is interesting to note that the TS indices for the long-term trend of SIC were much lower than those for March and September SIC. It was easier for the models to reproduce the climatological SIC than its long-term trend. For the TS indices of the same feature (either the SIC trend or SIC), the variability of the TS indices from different models may be used as a measure of the spread of the skill of these models. The standard deviation of the TS indices of the SIC trend for March, 0.20, was comparable to that of the long-term SIC trend for September, 0.21.This analysis shows that the spread in the skill of these models in reproducing the long-term SIC trend was roughly the same in March and September, indicating that it was equally challenging to reproduce the long-term SIC trends in both March and September. The correlation coefficient of the TS indices of March SIC and its long-term trend (0.80) was significant at the 95% level, whereas the correlation coefficient of the TS indices of September SIC and its long-term trend (0.43) was not. This may be attributed to the differences of the spatial distribution of March SIC and its long-term trend (Figures 2, 3, 6 and 7) compared with September SIC and its long-term trend(Figures 4, 5, 8 and 9). For March SIC, both the error and long-term trend were located at the margin of sea ice cover. However, for September SIC, the error of SIC existed both at the margin of sea ice cover and in the central part of the Arctic Basin. The long-term trend of September SIC was only located at the margin of sea ice cover.

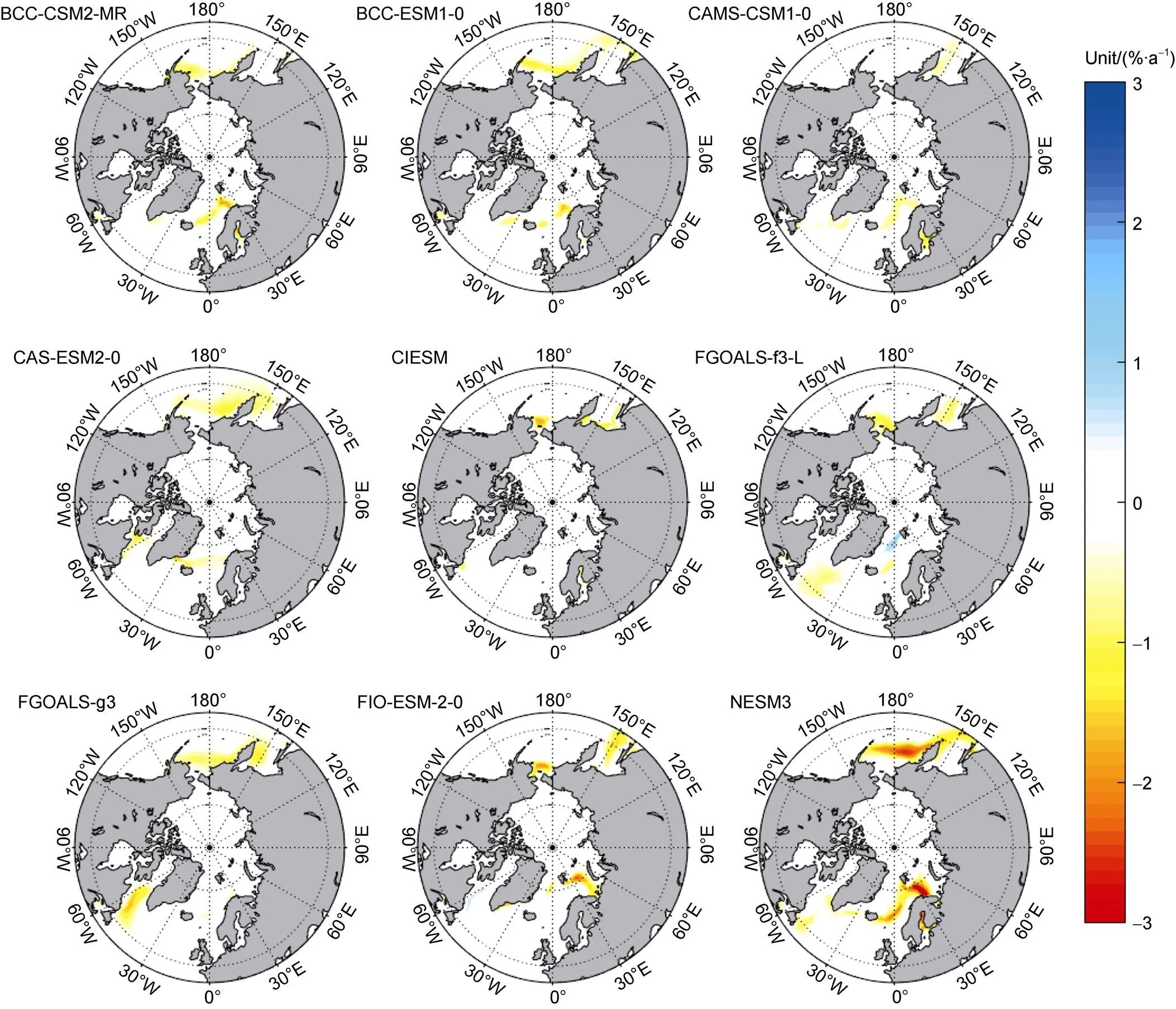
Figure 7 Spatial distribution of the 1980–2014 linear trendof Arctic SIC in March for nine models from China.

3.5 Comprehensive evaluation of model sea ice simulation

In the previous sections, we compared the sea ice simulations of nine models using different metrics of SIE and SIC. This section summarizes these metrics to comprehensively assess the sea ice simulation of each model. The metrics for SIE were the mean SIE in March and September, its standard deviation, the annual range of SIE, the long-term trends of SIE in March and September, and the annual trend of SIE. These eight metrics describe how well the model simulated the average, seasonal variability, and long-term trend of SIE. Regarding the spatial distribution of sea ice, the TS index was used to represent the spatial distribution of SIC and its long-term trends in March and September. The specific values of all metrics are given in Table 2. Bold numbers in columns 7, 8 and 9 indicate that the results were not significant at the 95% level for the linear trends: the September and annual trends of SIE from CAMS-CSM1-0, and the March, September, and annual trends from CIESM.

Figure 8 Spatial distribution of 1980–2014 linear trend of Arctic SIC in September from observation (a), 56 models (b), 9 Chinese models (c), root mean square error of linear trend of 56 models (d), and root mean square error of linear trend of 9 Chinese models calculated by formula (2) (e). The color bar for (a), (b), and (c) is shown vertically on the right and the color bar for (d) and (e) is shown horizontally on the bottom.

To compare the differences of the nine models for each metric and the overall simulation capability, Table 3 shows theevalues of 12 metrics for the nine models and the-scores obtained by combining all the metrics. The-scores in the last row were calculated following formulae (3) and (4). The computation of-scores used the 12 metrics from all 56 models to compare the nine models with the 56 CMIP6 models. In Table 3, rows 1 to 12 list theevalues calculated using single metrics following formula (5), which represent the skill of the model in reproducing the respective metrics. The value of the-score represents the difference between the model and the observation, and a smaller-score indicates that the simulation of the model was better.

Overall, several models, BCC-CSM2-MR, FGOLA- f3-L, and BCC-ESM1-0, had similar low-scores below or around 3, indicating that these models performed better in reproducing the historical variability of SIC and SIE. CIESM had the highest-score among the nine Chinese models because this model could not reproduce the sea ice variability in September, which was caused by overestimation of solar shortwave radiation, especially at high latitudes poleward of 60° (Lin et al., 2020). However, CIESM did have a lowevalue for March SIC. Another interesting example is FGOALS-g3. Although FGOALS-g3 had the second highest-score of the nine models, it could reproduce the annual and March SIE trends very well, indicating the limitation in evaluating coupled climate models using spatially integrated metrics such as SIE. Models can simulate the correct SIE with incorrect SIC. Future model evaluation should emphasize spatial distribution and diagnostic analysis of model output.

Theevalues of different metrics represent the relative skill of these models in reproducing the respective metrics. It is interesting to note that the variability ofevalues of the March and September long-term SIC trends was relatively small, indicating comparable skill of these models in reproducing the long-term SIC trend.

Figure 9 Spatial distribution of the 1980–2014 linear trendof Arctic SIC in September of nine models from China.

There were positive significant correlation coefficients between some of theevalues (Table 4). Theevalues of March SIC and September SIC were positively related with those of the long-term trends of March and September SIC, respectively. There were also positive correlations between September SIC and September SIE, September SIC and the standard deviation of September SIE, September SIC and the September SIE trend, and September and March SIC, indicating the important role of September sea ice simulation in the overall skill of a coupled climate model.

To compare the nine Chinese models with the 56 CMIP6 models, Figure 10 presents a histogram of the-scores of these 56 models with the-scores of the nine Chinese models, shown as vertical lines. The-scores of the 56 model had a wide spread, with a median value as 2.91, and the 25th and 75th percentile values were 2.41 and 4.03, respectively. Five of the nine Chinese models were within the 25th and 75th percentiles, indicating that these five models had skill comparable with the majority of CMIP6 models in reproducing Arctic sea ice variability, especially its seasonal cycle and long-term trend.

4 Conclusion

Nine coupled climate models from China participating in CMIP6 were evaluated in terms of historical Arctic sea ice simulation, especially SIE and SIC, in the context of 56 CMIP6 models. The ensemble SIE and SIC results of Arctic sea ice simulation by these models from 1980 to 2014 were compared against satellite observation using 12 metrics and ultimately a single comprehensive-score. These metrics included those for spatially integrated variables, such as SIE and the standard deviation of SIE for March and September, the long-term trends of SIE in March and September, the annual range, and the trend of SIE. The spatial distribution of SIC and its long-term trend were evaluated based on the Taylor score, which combines the spatial pattern correlation and spatial variability of two fields.

Table 3 E-Score of 12 Arctic sea ice metrics from Table 2. E-Scores are calculated from formulae (3) and (4). Rows 1 to 12 are the skill score calculated using a single metric following formula (5), and the last row is the E-Score calculated using all 12 sea ice metrics

Table 4 Correlation coefficients of skill scores of different metrics

Note: * indicate that 95% significance level tests have been passed, respectively

In terms of SIE simulation, eight of the nine models had skill comparable to that of other CMIP6 models, whereas one model severely underestimated September SIE. The nine models tended to overestimate Arctic SIE, especially for March, and underestimate the long-term trend of SIE. Seven of the nine models overestimated March SIE. Five of the nine models underestimated the long-term trend of September SIE. Seven of the nine models underestimated the annual trend of SIE.

For March, all models could simulate the spatial distribution of mean SIC reasonably well. The errors were mainly distributed at the margin of sea ice cover, and the errors were the largest in the middle of the Sea of Okhotsk, the Nordic Seas, and the Barents Sea, with the maximum value reaching 90%. Compared with the result for March, the spatial distribution of September SIC error was spread over a broader region. Errors existed both in the central part of the Arctic Basin and at the margin of sea ice cover. There was greater spread of model skill in reproducing September SIC than in reproducing March SIC.

The region with significant long-term trends of SIC in both March and September was the margin of sea ice cover. Satellite observations showed a decline trend in March SIC in the Nordic Seas, Barents Sea, and Sea of Okhotsk, with a slight increase in SIC south of the Bering Strait. All nine models failed to reproduce the trend of increasing SIC south of the Bering Strait. BCC-CSM2-MR, FIO-ESM-2-0, and NESM3 could reproduce the decline trend of SIC in the Nordic Seas and the Barents Sea to a certain extent. For September, models encountered greater difficulty reproducing the SIC decline trend from the Beaufort Sea to the Laptev Sea and Kara Sea in terms of spatial distribution and magnitude. The error in SIC simulation influenced the simulation of the long-term trend by shifting the spatial distribution of SIC.

Figure 10 The histogram of-score of 56 CMIP6 models. The-score of the nine Chinese models are shown as vertical lines.

Based on 12 metrics from the 56 CMIP6 models, a comprehensive metric, the-score, was computed to compare the sea ice simulation of the nine Chinese models with that of the other CMIP6 models. Several of the Chinese models had relatively high skill in reproducing Arctic sea ice, such as BCC-CSM2-MR, FGOALS-f3-L, and BCC-ESM1-0. However, some models could outperform other models for certain aspects. The-scores of the 56 CMIP6 models had a wide spread. Five of the nine Chinese models had-scores within the 25th and 75th percentiles of the 56 CMIP6 models, and had skill comparable with the majority of the CMIP6 models. In the present work, we only discuss the simulation results for Arctic sea ice. More detailed research is needed to diagnose and analyze the causes of model simulation error and determine how these models can be improved.

This study was supported by the National Key R&D Program of China (Grant no. 2018YFA0605904). The sea ice concentration data from the United States National Snow and Ice Data Center (NSIDC) are available from http://nsidc.org/data/seaice/. The CMIP6 data can be obtained from the Earth System Grid Federation nodes (https://esgf-node.llnl.gov/search/cmip6/). Insightful and detailed comments from two anonymous reviewers, and Assocaite Editor Michiel van den Broeke helped us greatly in revising the manuscript.

Cao J, Ma L B, Li J, et al. 2019. Introduction of NUIST-ESM model and its CMIP6 activities. Clim Change Res, 15(5): 566-570 (in Chinese with English abstract).

Cao J, Wang B, Yang Y M, et al. 2018. The NUIST Earth System Model (NESM) version 3: description and preliminary evaluation. Geosci Model Dev, 11(7): 2975-2993, doi:10.5194/gmd-11-2975-2018.

Eyring V, Bony S, Meehl G A, et al. 2016. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci Model Dev, 9(5): 1937-1958, doi:10.5194/ gmd-9-1937-2016.

He B, Bao Q, Wang X C, et al. 2019. CAS FGOALS-f3-L model datasets for CMIP6 historical atmospheric model intercomparison project simulation. Adv Atmos Sci, 36(8): 771-778, doi:10.1007/s00376- 019-9027-8.

He B, Liu Y M, Wu G X, et al. 2020. CAS FGOALS-f3-L model datasets for CMIP6 GMMIP Tier-1 and Tier-3 experiments. Adv Atmos Sci, 37(1): 18-28, doi:10.1007/s00376-019-9085-y.

Huang F, Zhou X, Wang H. 2017. Arctic sea ice in CMIP5 climate model projections and their seasonal variability. Acta Oceanol Sin, 36(8): 1-8, doi:10.1007/s13131-017-1029-8.

Hunke E, Allard R, Bailey D, et al. 2020. CICE-Consortium/CICE: CICE 6.1.4 (6.1.4). Zenodo, doi:10.5281/zenodo.4359860.

Lin Y, Huang X, Liang Y, et al. 2020. Community Integrated Earth System Model (CIESM): description and evaluation. J Adv Model Earth Sy, 12(8): e2019MS002036, doi: 10.1029/2019MS002036.

Lin Y L, Huang X M, Liang Y S, et al. 2019. The Community Integrated Earth System Model (CIESM) from Tsinghua University and its plan for CMIP6 experiments. Clim Change Res, 15(5): 545-550 (in Chinese with English abstract).

Long M, Zhang L, Hu S, et al. 2021. Multi-aspect assessment of CMIP6 models for Arctic sea ice simulation. J Clim, 34(4): 1515-1529, doi:10.1175/jcli-d-20-0522.1.

Meier W N, Fetterer F, Savoie M, et al. 2017. NOAA/NSIDC Climate Data Record of Passive Microwave Sea Ice Concentration, Version 3. Boulder: National Snow and Ice Data Center, doi:/10.7265/N59P2ZTG.

Notz D, IMIP Community. 2020. Arctic sea ice in CMIP6. Geophys Res Lett, 47(9): e2019GL086749, doi:10.1029/ 2019GL086749.

Peng G, Meier W. 2018. Temporal and regional variability of Arctic sea-ice coverage from satellite data. Ann Glaciol, 59(76pt2), 191-199, doi:10.1017/aog.2017.32.

Qiu B, Zhang L J, Chu M, et al. 2015. Performance analysis of Arctic sea ice simulation in climate system models. Chin J Polar Res, 27(1): 47-55, doi:10.13679/j.jdyj.2015.1.047 (in Chinese with English abstract).

Rong X Y, Li J, Chen H M, et al. 2018. The CAMS climate system model and a basic evaluation of its climatology and climate variability simulation. J Meteorol Res, 32(6): 839-861, doi:10.1007/s13351- 018-8058-x.

Rong X Y, Li J, Chen H M, et al. 2019. Introduction of CAMS-CSM model and its participation in CMIP6. Clim Change Res, 15(5): 540-544 (in Chinese with English abstract).

Shen Z, Duan A, Li D, et al. 2021. Assessment and ranking of climate models in Arctic sea ice cover simulation: from CMIP5 to CMIP6. J Clim, 34(9):3609-3627.

Shu Q, Qiao F L, Song Z Y, et al. 2013. The hindcast and forecast of Arctic sea ice from FIO-ESM. Acta Oceanol Sin, 35(5): 37-45 (in Chinese with English abstract).

Shu Q, Wang Q, Song Z, et al. 2020. Assessment of sea ice extent in CMIP6 with comparison to observations and CMIP5. Geophys Res Lett, 47(9): e2020GL087965, doi:10.1029/2020gl087965.

Song Z Y, Bao Y, Qiao F L. 2019. Introduction of FIO-ESM v2.0 and its participation plan in CMIP6 experiments. Clim Change Res, 15(5): 558-565 (in Chinese with English abstract).

Stroeve J C, Kattsov V, Barrett A, et al. 2012. Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations. Geophys Res Lett, 39(16): L16502, doi:10.1029/2012gl052676.

Tang Y L, Yu Y Q, Li L J, et al. 2019. The introduction of FGOALS-g model and the experiment design in CMIP6. Clim Change Res, 15(5): 551-557 (in Chinese with English abstract).

Taylor K E. 2001. Summarizing multiple aspects of model performance in a single diagram. J Geophys Res, 106(D7): 7183-7192, doi:10.1029/ 2000jd900719.

Wang S, Su J, Chu M, et al. 2020. Comparison of simulation results of the Arctic sea ice by BCC_CSM: CMIP5 and CMIP6 historical experiments. Haiyang Xuebao, 42(5): 49-64 (in Chinese with English abstract).

Watts M, Maslowski W, Lee Y J, et al. 2021. A spatial evaluation of Arctic sea ice and regional limitations in CMIP6 historical simulations. J Clim, 34(15): 6399-6420, doi:10.1175/jcli-d-20-0491.1.

Winton M. 2000. A reformulated three-layer sea ice model. J Atmos Oceanic Technol, 17(4): 525-531, doi:10.1175/1520- 0426(2000)017< 0525: artlsi>2.0.co;2.

Wu T W, Lu Y X, Fang Y J, et al. 2019.The Beijing Climate Center Climate System Model (BCC-CSM): main progress from CMIP5 to CMIP6. Geosci Model Dev, 12(4): 1573-1600, doi: 10.5194/gmd- 12-1573-2019.

Xu S, Song M, Liu J, et al. 2013. Simulation of sea ice in FGOALS-g2: climatology and late 20th century changes. Adv Atmos Sci, 30(3): 658-673, doi:10.1007/s00376-013-2158-4.

Zhou G Q, Zhang Y Q, Jiang J R, et al. 2020. Earth system model: CAS-ESM. Front Data Comput, 2(1): 38-54.

Zhou T J, Zou L W, Chen X L. 2019. Commentary on the Coupled Model Intercomparison Project Phase 6 (CMIP6). Clim Change Res, 15(5): 445-456 (in Chinese with English abstract).

10.13679/j.advps.2022.0098

1 July 2021;

22 August 2022;

30 September 2022

: Li J Q, Wang X C, Wang Z Q, et al.Evaluation of Arctic sea ice simulation of CMIP6 models from China. Adv Polar Sci, 2022, 33(3): 220-234,doi:10.13679/j.advps.2022.0098

, ORCID: 0000-0003-2193-4964, E-mail: xcwang@nuist.edu.cn