基于ANSYS的H型刚柔耦合机械臂动力学建模与动态特性机理研究
闻 志,沈金淼,孔 辉,张文辉,4,5,游张平
(1.浙江理工大学机械工程学院,浙江 杭州 310018;2.南京晓庄学院电子工程学院,江苏 南京 211167;3.丽水学院工学院,浙江 丽水 323000;4.浙江省航空航天金属导管塑性成形技术与装备重点实验室,浙江 丽水 323000;5.浙江省文创产品数字化设计与智能制造重点实验室,浙江 丽水 323000)
自从20世纪60年代第一台机器人诞生以来,机器人技术[1]在学术研究、工业生产等方面得到了飞速发展。机械臂作为一种特殊的机械结构[2],因其具有轻型化、高效性、独立性等优点[3],并且能够完成高精度、高要求、高危险等任务,被越来越多地应用在航空、医疗、军事、工业生产等领域[4-6]。随着科学技术的不断发展,对机械臂的要求也越来越高,对机械臂而言,轻型化、高速度、高精度是现代设计的必然要求[7],整个机械系统演变为刚体与柔性体相耦合的动力系统[8]。在高精确运动要求前提下,就必须考虑机械臂的弹性变形对运动精度的影响[9-10]。因此,笔者从柔性宏刚性微机械臂的优化设计角度,对刚柔耦合机械臂的动态特性及内在机理进行分析研究。
柔性操作臂是典型的刚柔耦合非线性动力学系统,研究其动力学特性问题,需要建立系统的动力学模型。近年来,宏柔微刚机械臂被越来越多的学者所研究[11-12]。崔玲丽等[13]考虑机械臂的形状参数及驱动器的参数,基于有限元分析法,构建了非均匀截面梁系统的动力学模型;Kane等[14]基于模态综合法对运动基柔性梁建立了较为准确的动力学方程,对系统的动力学特性进行了研究;王从庆等[15-17]又采用拉格朗日法推导了平面三连杆刚柔耦合机械臂的动力学模型,并通过实验测试验证了该模型的合理性;Yang等[18]学者基于假设模态法,利用传感器测得的柔性操作臂线性位移以及关节转角推导了柔性多连杆操作臂的动力学模型;Khairudin等[19]学者利用拉格朗日方程及假设模态法推导了双连杆柔性操作臂的动力学模型。
考虑到柔性宏刚性微机械臂是一个多变量、非线性复杂的动力学系统,故要想全面了解其动力学动态特性,有必要对其固有频率特性和内在机理进行深入研究。首先,基于有限元法和拉格朗日方程完成对柔性多体系统动力学模型的构建;其次,分别从截面参数、材质组合、集中质量等方面分析各因素对系统固有频率特性的影响,研究各参量与刚柔机械臂固有频率之间的关系,分析不同设计参量对宏微机械臂固有频率特性的影响规律和作用机理。
1 柔性宏刚性微机械臂模型建立
机械臂的模型建立是其动态特性分析的重要内容,是系统整体结构设计和优化的前提。精确的动力学模型也为控制系统描述及控制器设计提供有效的依据。动力学建模通常是基于混合坐标的建模方法,当系统做大规模运动时,自身结构发生弹性变形,具有较强的刚柔耦合性。笔者基于弹性动力学分析方法通过离散机械臂单元自由度,描述机械臂的弹性变形,为后续进一步研究柔性宏刚性微机械臂的动态特性奠定了基础。
柔性宏刚性微机械臂的系统模型如图1所示。当分析其弹性变形时,假设杆1、杆2分别为单个结构单元体。
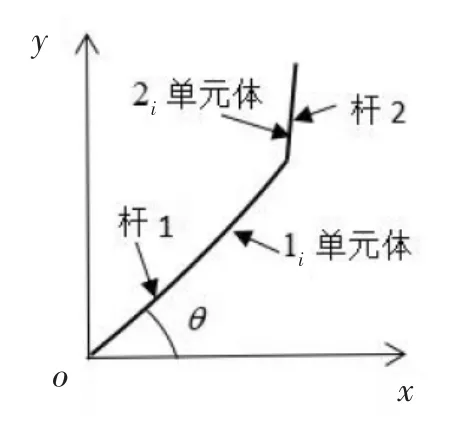
图1 宏柔微刚机械臂系统模型
系统的运动微分方程一般表示为
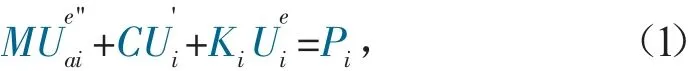
式中:M表示质量矩阵;C表示阻尼矩阵;K表示刚度矩阵;P表示广义力矩阵;表示一个8维列阵;U表示弹性位移矩阵。与U满足以下关系:

其中Bi表示一个8×9的坐标协调矩阵。
同理,有

将式(2)和式(3)代入式(1),并左乘得

式中:

将所有单元运动方程相叠加即可得到柔性宏刚性微机械臂系统运动方程为

2 柔性宏刚性微机械臂固有频率分析
2.1 频率特性参量定义
由弹性动力学分析方法可知,系统的动力学方程式为

式中:M为质量矩阵;K为刚度矩阵;P为广义力矩阵;U为弹性位移列阵;为弹性加速度列阵。
固有频率w可由式(9)的特征根求得,即

式中,I为单位矩阵。
由式(10,11)可知系统的固有频率w与质量矩阵和刚度矩阵有关。
由此可得每一个单元体固有频率的表达式为

式中:mi为单个单元体质量矩阵;ki为单个单元体刚度矩阵。其中,
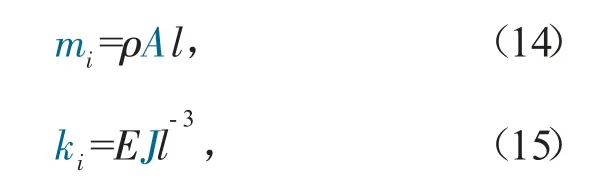
式中:l为机械臂单元长度;ρ、E分别为杆件材料的密度和弹性模量;J、A分别为单元的截面面积和惯性矩。
综上所述,联合式(12)、式(15)可推导出如下关系式为

2.2 不同截面参量对刚柔机械臂固有频率影响分析
弹性机构常见的几种截面类型有:实心圆柱、空心圆柱、H型、实心矩形、空心矩形等,具体参数如表1所示。

表1 不同截面类型参数表
相同臂杆长度、相同材质的情况下,5种截面机械臂杆件的前两阶系统固有频率变化规律如图2所示。

图2 机械臂固有频率参数图
由图2可知:截面为实心矩形的刚柔机械臂固有频率最低,空心矩形和实心圆形其次,H型再次,空心圆形的固有频率最高。其中,H型是介于空心和实心之间的一种截面形态,由图可以看出,其机械臂各阶频率均较高,且整体曲线较光滑,系统整体稳定性较高。因此,笔者选取截面类型为H型的宏柔微刚机械臂来探究其结构、材质等参量对其固有频率特性的影响,为后续整体优化设计提供参考依据。
2.3 H型宏微机械臂参数对频率特性影响分析
定义H型杆件材料为碳钢,杆件弹性模量E=207 GPa,密度ρ=7 850 kg/m3,柔性机械臂长度L1=1 m,截面宽度B1=45 mm,截面壁厚H1=45 mm,腹板厚b1=10 mm,翼缘厚h1=15 mm;刚性机械臂长度L2=0.5 m,截面宽度B2=6 mm,截面壁厚H2=20 mm,腹板厚b2=6 mm,翼缘厚h2=9 mm。
机械臂关节角运动规律为
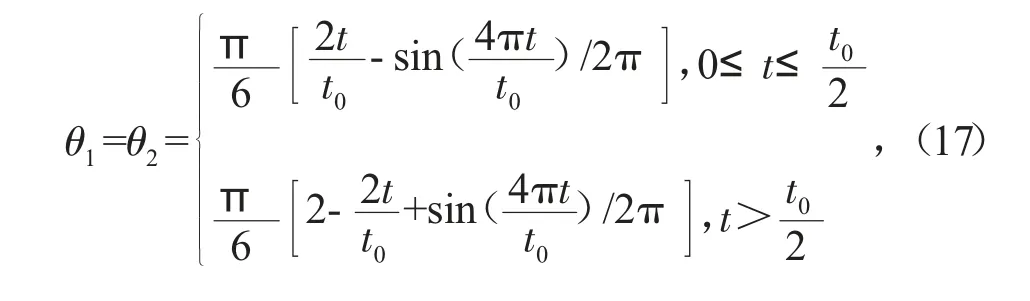
式中:t0表示运动周期,选取t0=3.0 s。
2.3.1 结构参量对固有频率的影响
笔者主要从以下两种方式进行研究:保证刚柔机械臂长度比值不变,同比改变它们的长度;保证刚柔机械臂总长度不变,同比改变它们的长度比。通过上面两种方式进行实验得到机械臂运动规律。
1)同比改变刚柔机械臂的长度。
在保证横截面积、材料等参量不变的情况下,分别考虑:初始长度、同比增加50%、同比增加100%这3种机械臂宏微杆长度的固有频率变化规律,得到如图3所示前两阶固有频率变化曲线。

图3 H型杆件长度比值不变情况下固有频率参数变化曲线
由系统前两阶固有频率变化曲线可以看出:在保证横截面积、材料等参量不变情况下,随着H型宏微机械臂杆长的增加,各阶固有频率随之减小。因此,减少宏微机械臂总体长度有利于提高系统的固有频率。
2)同比改变刚柔机械臂的长度比。
保证柔性宏刚性微机械臂的总长度L总=1 500 mm,分别取比值为3:1、5:1、10:1的3种机械臂长度,得到如图4所示前两阶固有频率变化曲线。
由图4可以看出:3种情况下的固有频率无论一阶还是二阶都呈现依次递减的情况,其中,柔性杆件占比越小系统越稳定。因此,降低柔性臂杆的占比,有利于提高固有频率。

图4 H型杆件长度比值改变情况下固有频率参数变化曲线
2.3.2 材质参量对固有频率的影响
前面的研究采用的是碳钢材料,考虑到铝材的轻质特性,下面将采用碳钢和铝材进行搭配分析:全为钢材料;全为铝材料;钢铝混合(柔性臂采用钢材料,刚性臂采用铝材料)。铝材料的参数如下:弹性模量E=70 GPa,密度ρ=2 700 kg/m3。3种情况下系统的固有频率变化曲线如图5所示。
从图5变化曲线及各界频率数值可知:全钢和全铝的柔性宏刚性微机械臂固有频率比较接近,而“柔性宏钢+刚性微铝”这一混合式搭配相比全钢和全铝则表现出杰出的性能,其固有频率远大于其他2种。这一结论对于柔性机械臂性能提升具有重要意义。

图5 H型杆件不同材料情况下固有频率参数变化曲线
2.3.3 集中质量参量对固有频率的影响
同理,笔者主要从以下2个角度探究集中质量参量对系统固有频率特性的影响规律。
1)保证关节点集中质量不变,仅改变末端点集中质量。
在保持其他各类影响因素不变或者是相同的情况下,杆件末端加入不同的质量:m1=0 kg、m2=1 kg、m3=2 kg,进行实验仿真得到固有频率曲线如图6所示。

图6 H型杆件末端添加质量情况下固有频率变化曲线
由图6可知:随着末端集中质量的逐渐变大,固有频率逐渐降低。这说明末端集中质量对机械臂固有频率具有较大影响,且成反比关系,降低末端质量有利于提高机械臂固有频率。
2)关节点和末端点依次增加集中质量。
依次在柔性臂的关节点1、关节点2及末端点增加1 kg的集中质量,即第一次关节点1处1 kg,第二次关节点1处1 kg+关节点2处1 kg,第三次关节点1处1 kg+关节点2处1 kg+末端质量1 kg。3种情况下固有频率变化曲线如图7所示。

图7 H型关节点和末端添加质量情况下固有频率变化曲线
由图7可知:随着质量的逐渐加大,固有频率逐渐降低,而且其变化呈现较为严重的非线性,其中末端质量对机械臂动态特性影响最为严重,这是由于末端质量距离机械臂基座最远,其惯性力矩也最大。因此,在不改变宏微机械臂其他参量的情况下,尽量降低微机械臂的质量,特别是末端质量,可以有效地提高系统的固有频率。
3 结论
柔性宏刚性微机械臂作为一种大范围高速精密机构,对其固有频率特性和内在机理进行深入研究具有重要意义。
1)基于有限元法和拉格朗日方程,建立刚柔机械臂的柔性多体系统动力学模型。
2)研究不同截面刚柔机械臂固有频率特性的影响规律,H型的宏柔微刚机械臂各阶频率均较高,且整体曲线较光滑,系统整体稳定性较高。
3)研究发现:相同外形尺寸情况下,H型刚柔机械臂不仅质量更轻,而且固有频率更高;随着等比长度的增加,固有频率呈现急剧减小趋势;采用柔性钢微性铝机械臂相比全钢或全铝,固有频率大幅提升;在保持其他参量不变的条件下,降低末端质量有利于提高机械臂固有频率。
通过以上分析为进一步研究H型刚柔机械臂整体优化设计提供了理论依据,对改善刚柔机械臂系统性能具有重要指导作用。

