拓展的（2+1）-维浅水波方程共振解

张尚雷，费金喜

（1.丽水市实验学校，浙江 丽水 323000；2.丽水学院工学院，浙江 丽水 323000）

在海洋学和大气科学中，利用（2+1）-维浅水波方程式

研究水波传播的动力学行为[1]。式（1）由Wazwaz[2]首次引入，根据Hereman简化方法和Cole-Hopf变换，附加项αuxy不会破坏可积性。Roshid和Ma[3]研究了式（1）的团块解。从已有文献中我们可获得式（1）的Wronskian、Pfaffian和周期波解。若α=0，则式（1）可约化为（2+1）-维Boiti-Leon-Manna-Pempinelli方程[4]。

拓展的（2+1）-维浅水波方程式为

其中α和β为任意常数。在非线性水波中，式（2）更能反映出丰富的物理意义。设v=uy，w=ux，式（2）可写为

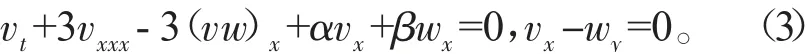
1 方程（3）的双线性形式和多孤子解

通过因变量变换

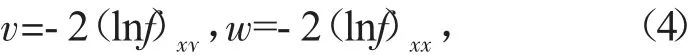
得到方程（3）的双线性形式

式（5）中：f=f（x，y，t）；D为Hirota微分算子，定义

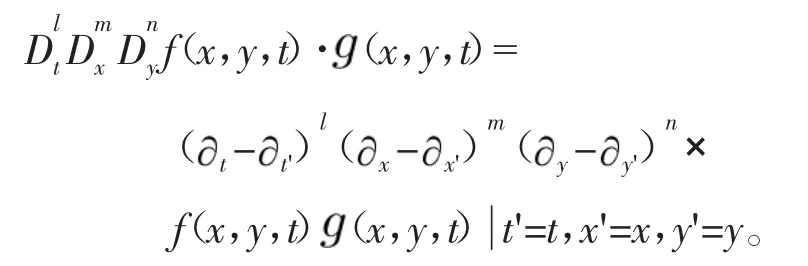
由式（5）可知，多孤子的表达式为

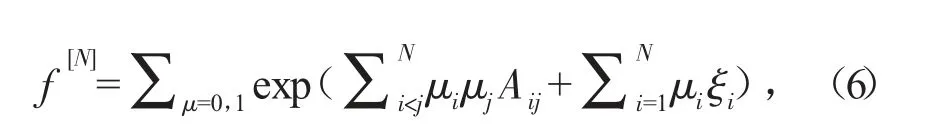
其中对μ的求和取μj=0,1（j=1，2，…，n）的所有可能的组合，且

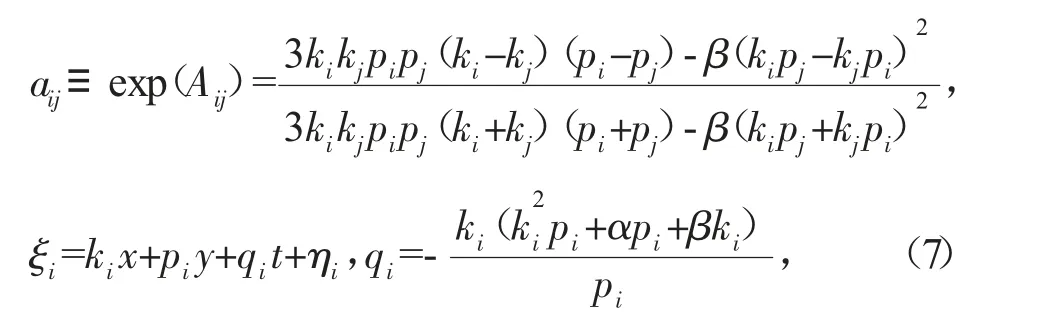
其中ki、pi、ηi（i=1，2，…，n）为任意常数。将式（6）代入式（4）得到方程（3）的多孤子解为

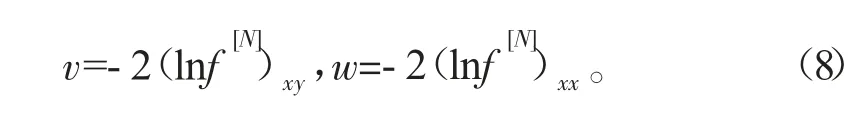
2 N=2时方程（3）的典型解

2.1 二孤子的共振解

当N=2时，令a12=0，则式（6）变为

色散关系满足

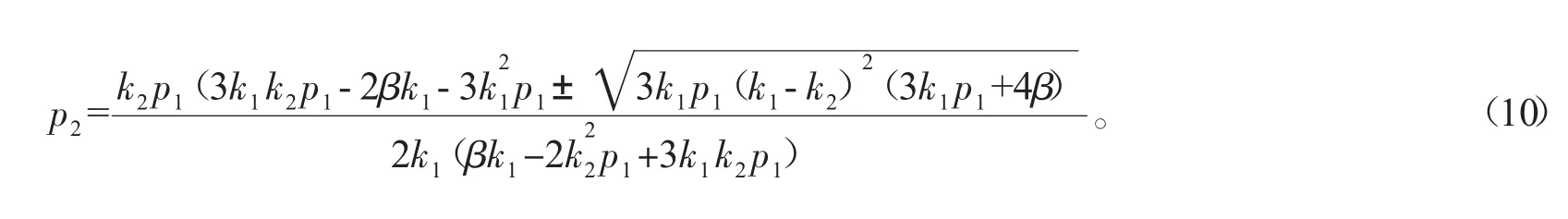
由式（8～10）得到方程（3）的二孤子共振解，称为Y-型孤子解[5]，它的传播速度在x和y方向上的分量分别为

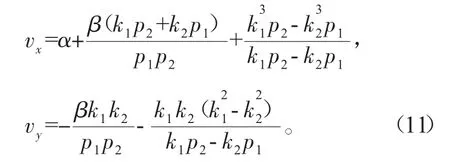
Y-型孤子随时间变化的传播情形，如图1所示。图1中的参数为

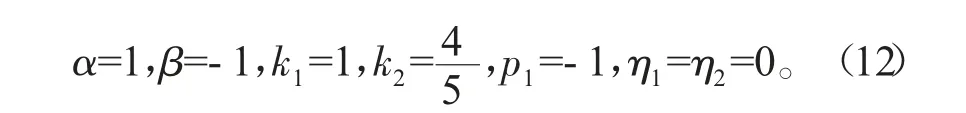
从图1中我们可以看出：Y-型孤子的波形不随时间变化而改变，在x和y方向上的速度分量分别为vx=3.92，vy=0.92。

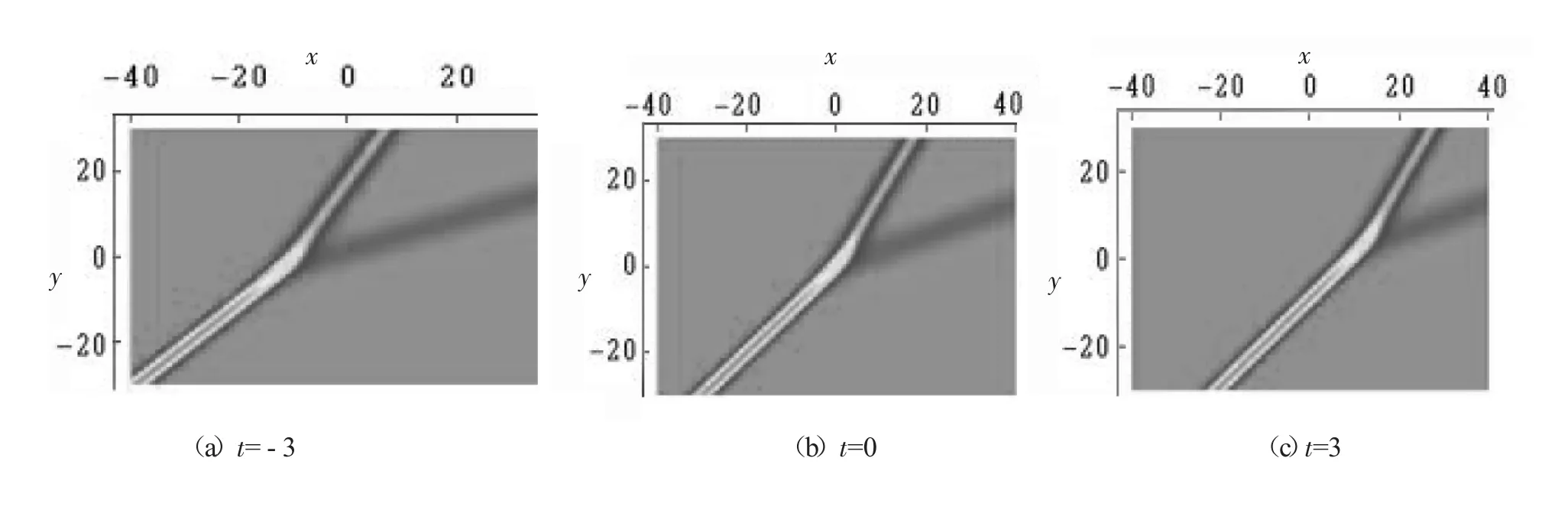
图1 Y-型孤子随时间变化传播情形的密度图

2.2 团块解

为了获得方程（3）的团块解，利用长波极限的方法，设

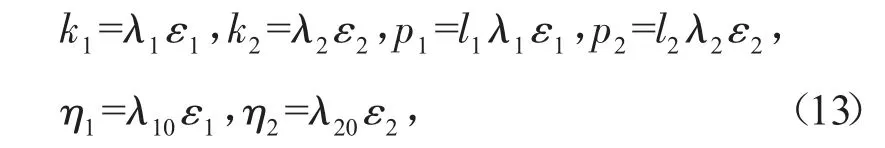
将式（6）在ε1→0，ε2→0处用Taylor级数展开，得

为了寻求团块解，须消除式（13）中的奇异点，设

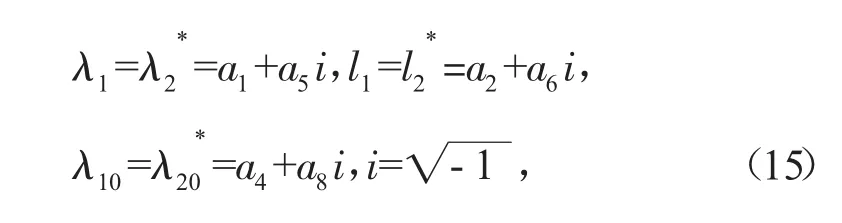
则式（14）变为

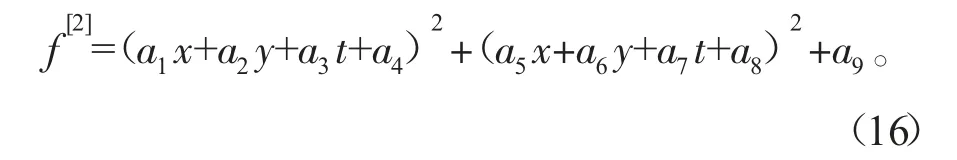
式（16）中：

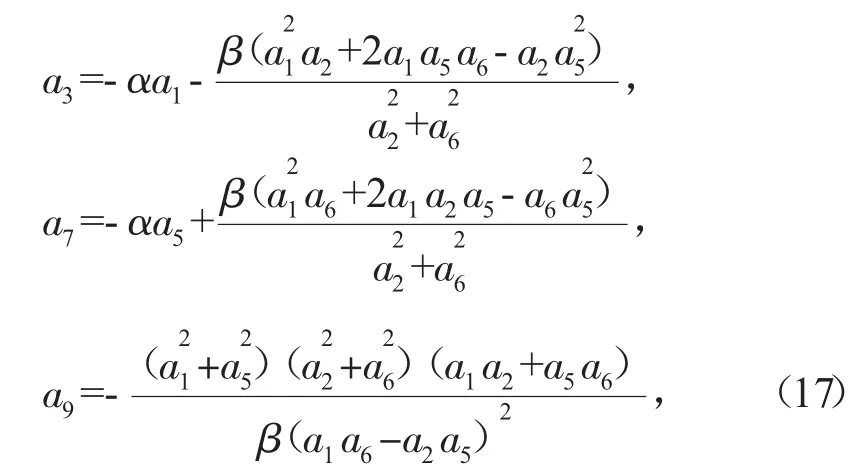
其中a1、a2、a4、a5、a6、a8为任意常数。将式（16）代入式（8）得到方程（3）的团块解。式（3）的传播速度在x和y方向上的分量分别为

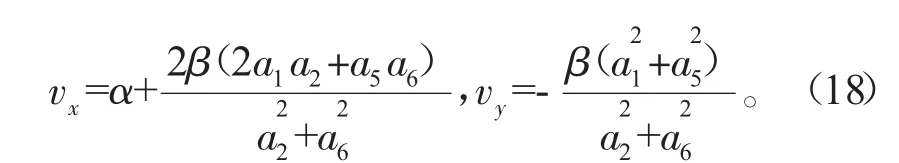
2.3 呼吸子解

为寻求方程（3）的呼吸子解，设

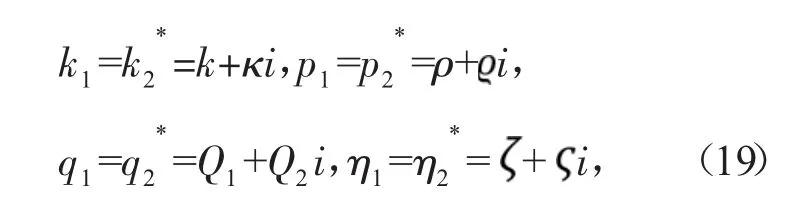
则式（6）可写为

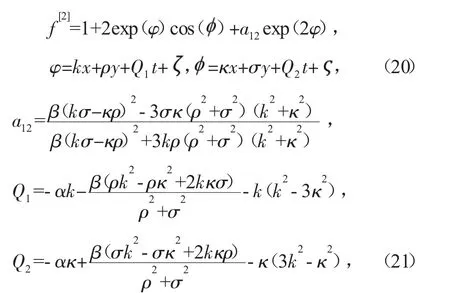
其中k、κ、ρ、σ、、分别为任意实常数。将式（18）代入式（8）获得方程（3）的呼吸子解。

3 当N=3时，方程（3）的共振解

3.1 Y-型孤子与孤子的共振解

令a12=0，则式（6）变为

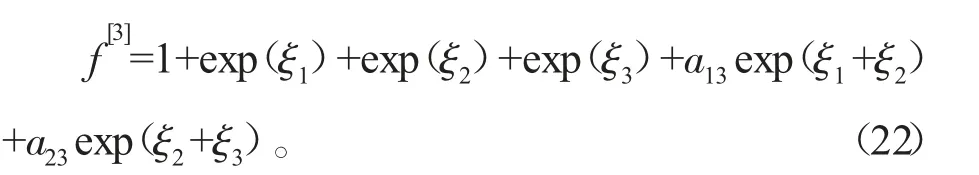
若Y-型孤子和单孤子满足速度共振条件：

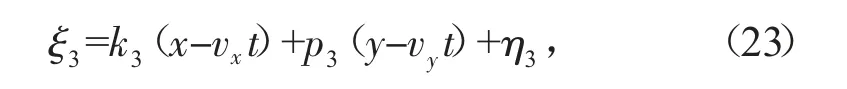
式中的vx、vy由（11）式确定，将式（22）代入式（8），则得到方程（3）的三孤子解。这三孤子解存在着特殊的结构。它由Y-型孤子和单孤子组成，且Y-型孤子和单孤子具有相同的运动速度，因而它们的相对位置不随时间的变化而改变。图2显示了Y-型孤子和单孤子叠加的共振解随时间变化传播情形的密度图。

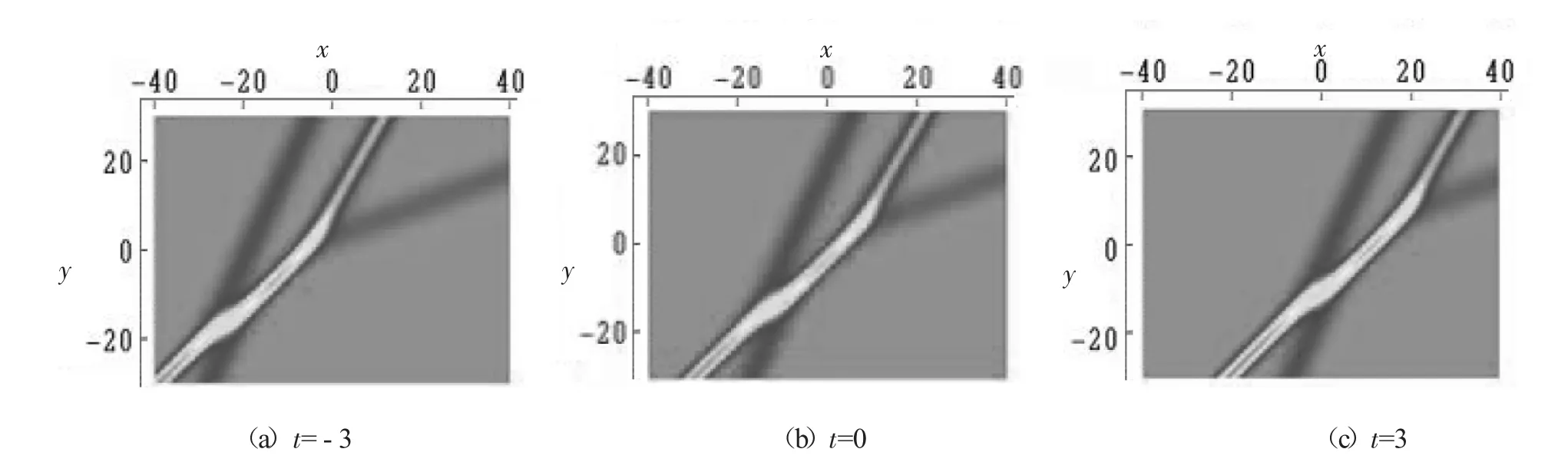
图2 Y-型孤子和单孤子叠加的共振解随时间变化传播情形的密度图

3.2 团块与孤子叠加的共振解

将式（13）代入式（6），并在ε1→0，ε2→0处，用Taylor级数展开，式（6）变为

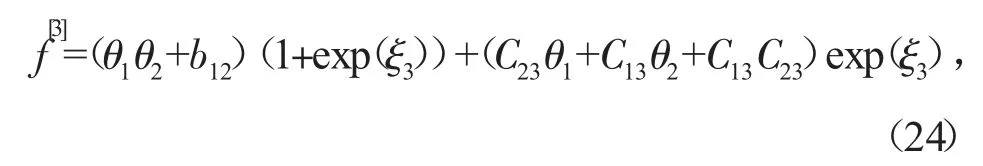
式中的θ1、θ2、b12由式（14）确定，C13、C23满足

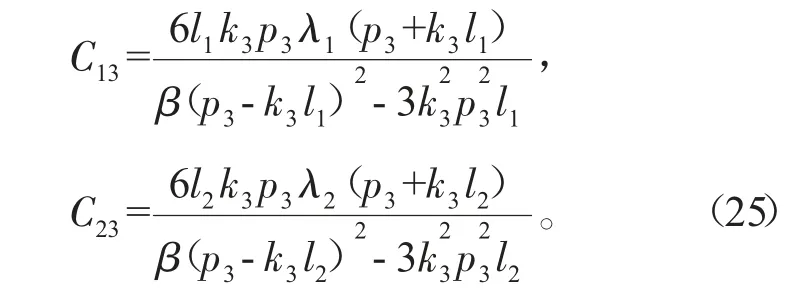
若团块和孤子满足速度共振条件：

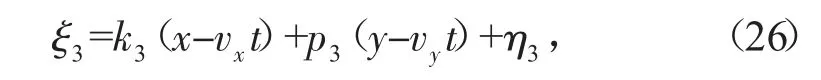
式中的vx、vy由式（18）确定，将式（24）代入式（8），则得到方程（3）的由团块和孤子叠加的共振解。这一共振解结构稳定，团块和孤子的相对位置不随时间变化而改变。图3显示了由团块和孤子叠加的共振解随时间变化的传播情形，图3中的参数为

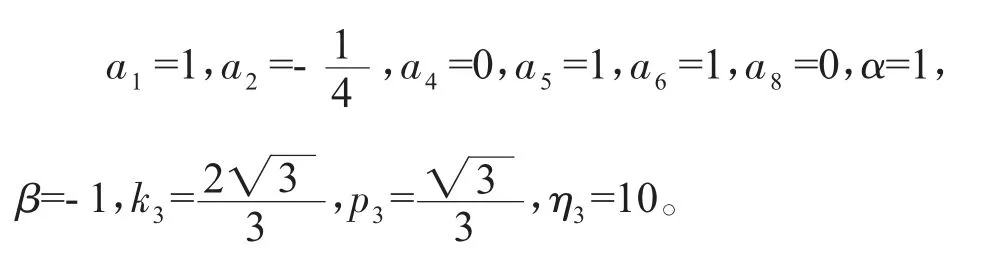
图3 由团块和孤子叠加的共振解随时间变化传播的密度图

3.3 呼吸子和孤子的共振解

将式（19）代入式（6），得到

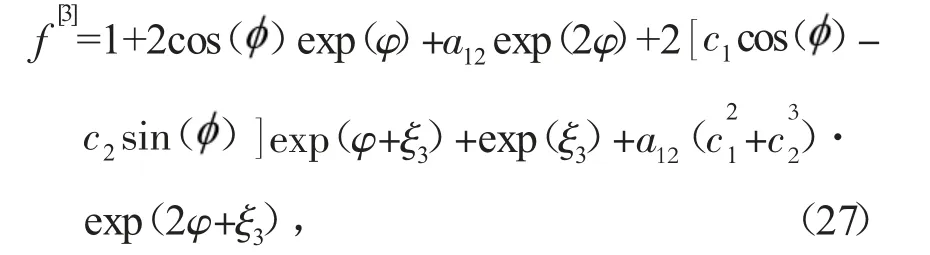
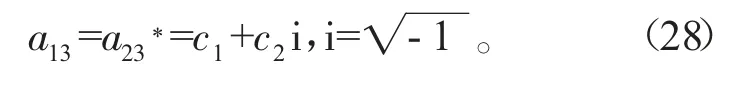
若呼吸子和孤子满足速度共振条件：

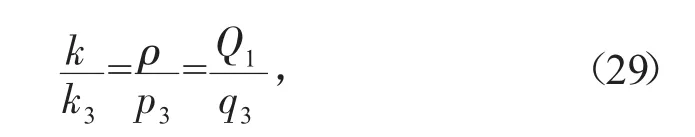
则得到由呼吸子和孤子叠加的共振解。图4显示了由呼吸子和孤子叠加的共振解随时间变化的传播情形，图4中的参数为

图4 由呼吸子和孤子叠加的共振解随时间变化传播的密度图

4 当N=4时，方程（3）的共振解

4.1 团块和双孤子的共振解

当N=4时，在式（13）的条件下，把式（6）在ε1→0，ε2→0处Taylor级数展开，得到

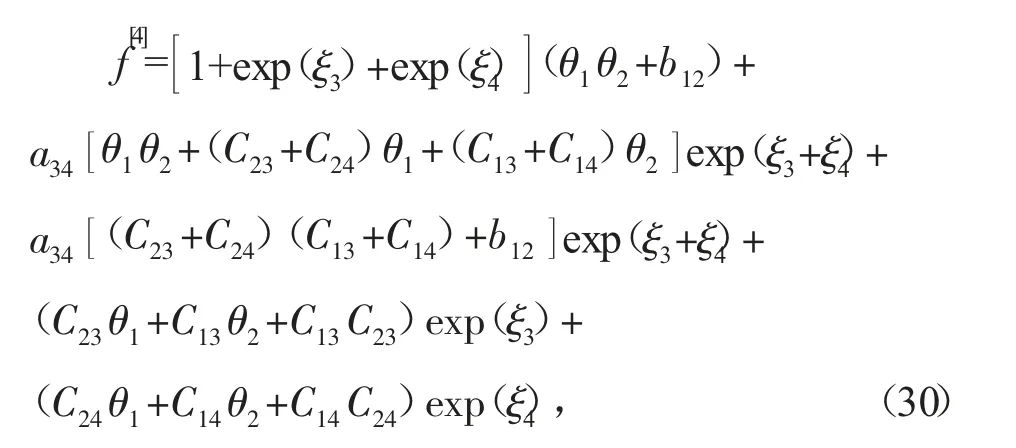
式（30）为一个团块和双孤子的相互作用解，其中θ1、θ2、b12和C13、C23分别由式（14）和（25）确定，C14、C24满足：

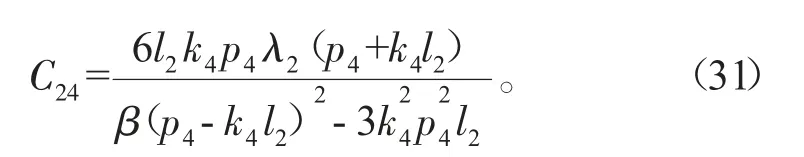
若团块和双孤子的运动速度相同，即

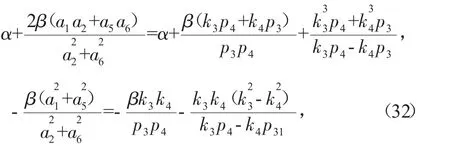
将式（30）代入式（4），则可获得团块和双孤子的共振解。图5展示了团块和双孤子的共振解随时间演化的密度图。图5中的参数为：

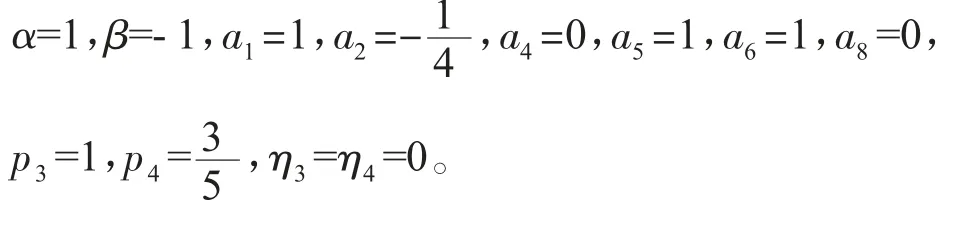
图5 由团块和双孤子叠加的共振解随时间变化传播的密度图

4.2 团块和呼吸子的共振解

对于式（30），进一步假设

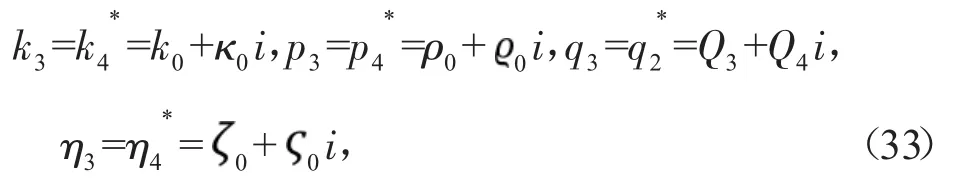
则其中的双孤子转化为呼吸子。若团块和呼吸子的运动速度相等，即满足速度共振条件：

其中

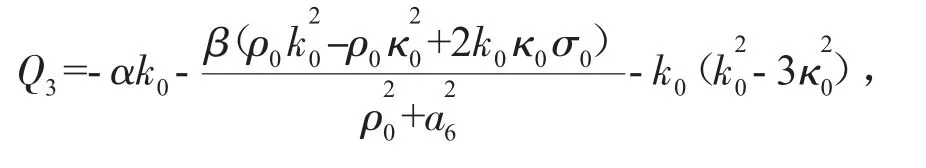
将式（30）代入式（8），则可获得团块和呼吸子的共振解。图6展示了团块和呼吸子的共振解随时间演化的密度图。图6中的参数为

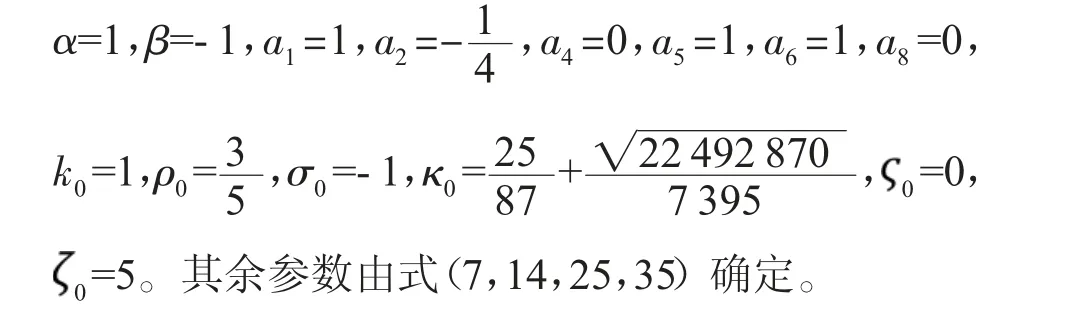
图6 由团块和呼吸子叠加的共振解随时间变化传播的密度图

4.3 两呼吸子的共振解

为寻求方程（3）的两呼吸子的混合解，在式（19，33）的假设下，式（6）可写为

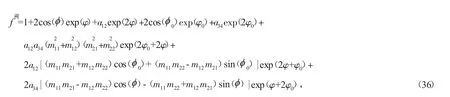
若两呼吸子的运动速度相等，即满足速度共振条件：

将式（37）代入式（8），则可获得两呼吸子的共振解。图7展示了两呼吸子的共振解随时间演化的密度图。图中的参数为

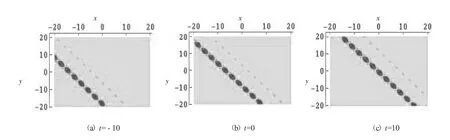
图7 由两呼吸子叠加的共振解随时间变化传播的密度图

5 结语

共振现象在自然界中普遍存在。笔者基于双线性形式，得到多孤子解，并在此基础上讨论了Y-型孤子及Y-型孤子与孤子、团块与孤子、呼吸子与孤子、团块与双孤子、团块与呼吸子、呼吸子与呼吸子的共振解，希望这些解对非线性科学和物理学有所应用和帮助。