基于分数阶MARS无传感器PMSM迭代学习控制

刘偲艳

（光伏发电系统控制与优化湖南省工程实验室，湖南 湘潭 411104）

永磁同步电机（PMSM）以其高功率密度、低转动惯量和高效率等显著优点，在现代工业领域及新能源领域具有广泛的应用[1]。某些高性能系统如新能源混合动力汽车、风力发电系统、航空航天等领域都广泛使用永磁同步电机，在进行电机驱动系统控制时离不开电机转速及位置信号的采集，目前常用的方法为安装高精度速度传感器。但是高精度速度传感器一方面增加驱动系统造价，另一方面增加系统故障风险。若传感器故障突然出现，轻则影响系统性能，重则造成重大事故及人员伤亡，所以该领域必须考虑传感器故障时电机驱动系统的容错控制。容错控制常用方法有备用高精度传感器和无速度传感器，无速度传感器为一种非硬件传感器，通过算法辨识电机转速、位置[2]，适应速度范围宽，价格低，从而受到国内外众多学者的重视。

PMSM无速度传感器利用电机绕组中相关信息，通过适当方法估计电机转子的位置和转速。目前主要的方法有基于观测器法[3-5]、高频信号注入法[6-7]及模型参考自适应法[8-11]。文献[3]采用扩展滑模观测器无速度传感法，能准确地估算电机转速和位置，但是系统抖动没有明显改善；文献[4]提出滑模观测器采用分段指数型函数代替传统滑模观测器中的开关函数，开关抖振问题得到改善；文献[7]采用在高频注入信号叠加直流偏置的方法估算转速，该方法具有适应速度范围宽、估算精度较高等优点，但直流偏置信号的叠加增加系统控制难度；文献[9]采用模型参考自适应控制，但该方法的精确度依赖于电机参数的准确性；文献[10]转速环增加滑模环节，提高系统的鲁棒性。

为提高PMSM转速估算的精确度，本文采用分数阶模型参考自适应无速度传感器，能实现转速突变时的准确估算。相较于整数阶模型参考自适应控制方法，分数阶模型参考自适应控制方法增加了分数阶可调参数、控制器参数自由度，具有更优异的控制性能。

迭代学习控制适用于具有重复性能的控制系统，可实现有限时间内的完全跟踪，且不依赖PMSM精确的数学模型。迭代学习控制具有开环和闭环两种，开环学习控制不能及时反馈系统迭代信息，闭环学习控制能及时反馈系统迭代信息，但是采用PD型迭代学习控制时，相对阶为1的误差信号导数实现困难[12]。本文为克服开/闭环控制的缺点，实现有限时间内期望转速快速的完全跟踪，提出一种增加辅助反馈项的PD迭代学习控制，该方法在传统PD型迭代学习控制基础上增加当前次迭代信息的P项，能增强系统的收敛性。

综上，本文提出一种基于分数阶模型参考自适应PMSM新型PD迭代学习控制策略，当电机转速突变时，能实现转速的准确估算及期望转速的精确跟踪，系统具有良好的动态性能。最后，Matlab/Simulink仿真及实验说明了方法的可靠性。

1 PMSM数学模型

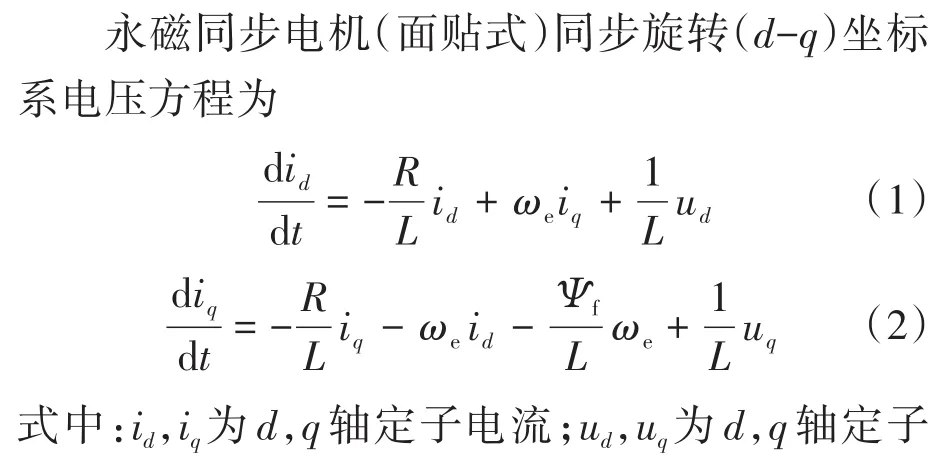
2 分数阶模型参考自适应观测器

2.1 可调模型设计

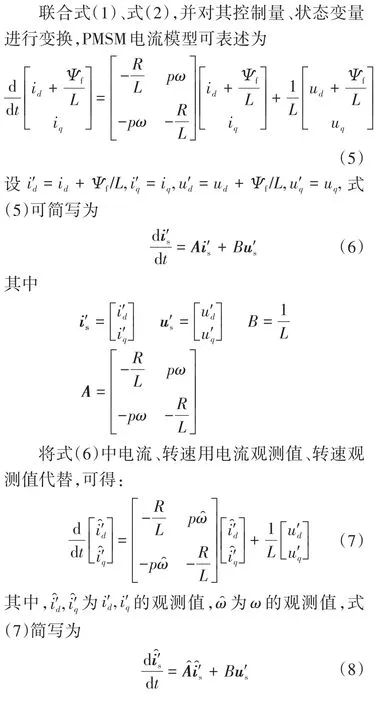
2.2 分数阶模型参考自适应率

2.3 Popov超稳定性理论

3 新型PD迭代学习控制

图1所示为迭代学习控制误差的Lebesgue-p范数，图1a为本文所提带反馈增益控制图，图1b为传统PI迭代学习控制图，由图可知PD-ILC收敛速度快。

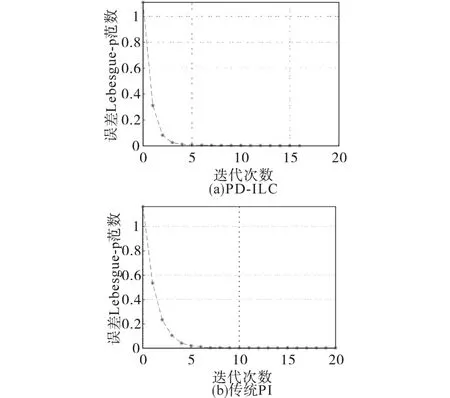
图1 误差的Lebesgue-p范数Fig.1 Lebesgue-p norm of error

4 仿真及实验验证

本文采用基于分数阶模型参考自适应PMSM新型PD-ILC控制策略结构框图如图2所示，永磁同步电机参数如下：定子电阻R=0.56 Ω，极对数p=3，转动惯量J=0.002 1 kg·m2，永磁磁链Ψf=0.82 Wb，定子电感L=0.015 3 H，黏滞摩擦系数B=0.000 1。

图2 系统控制框图Fig.2 Control block diagram system

1）定义最优性能（ITAE）指标函数为

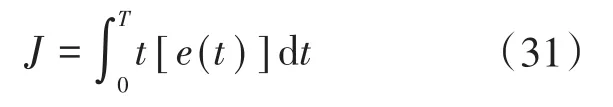
利用ITAE最小准则原理，通过寻优法可得其与在α（0，1）的变化关系。当电机期望速度为500 r/min时，逐渐增大α值，α=0.9时，ITAE指标最优。

2）主要验证所设计分数阶模型参考自适应观测器的有效性。控制器采用PI控制，观测器分别采用整数阶（α=1）和分数阶（α=0.9）模型参考自适应观测器进行仿真对比。

仿真试验条件设置：电机初始时刻期望速度为600 r/min，0.1 s时加12 N·m负载，调整其他参数一致。仿真结果如图3、图4所示。

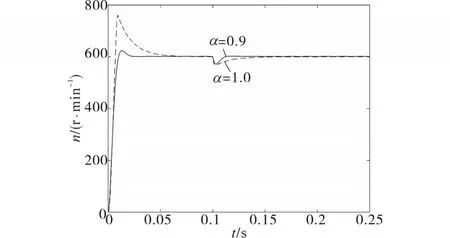
图3 电机输出对比图Fig.3 Comparison of motor output

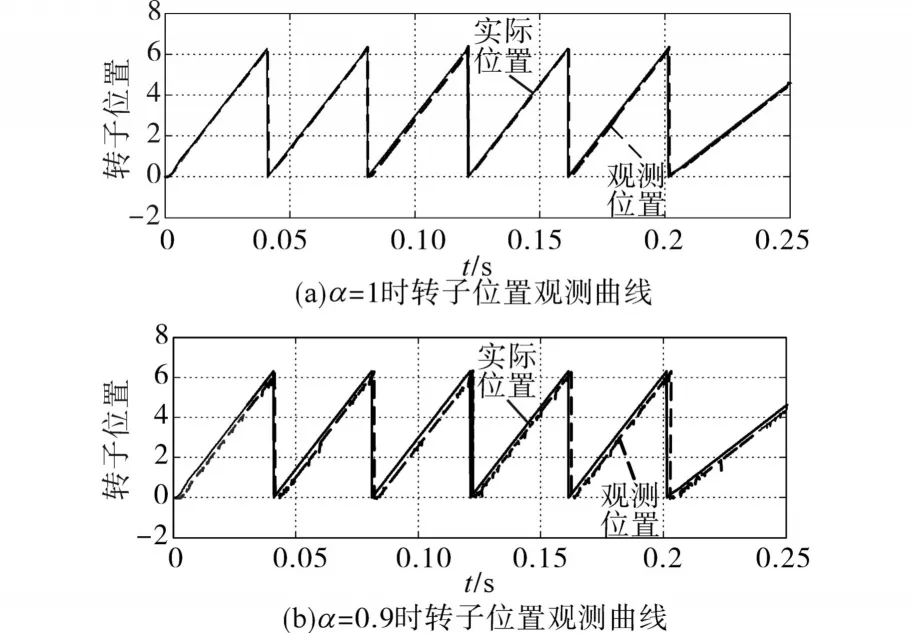
图4 转子位置观测对比图Fig.4 Comparison chart of rotor position estimation

图3为α=0.9，α=1时的转速观测曲线对比图，图中可以得出整数阶、分数阶模型参考自适应观测器均能稳定运行，且响应速度快，分数阶模型参考自适应观测器转速观测误差小于整数阶模型参考自适应观测转速观测误差，观测准确度更高。

图4a、图4b分别表示α=1，α=0.9时的转子位置观测曲线。对比分析图4a、图4b中数据显示可得，α=0.9时误差明显减小。

3）确定分数阶模型参考自适应有效性后，控制器分别采用PI控制和新型PD-ILC控制进行仿真对比分析。

变速仿真：系统初始0～0.1 s运行速度为600 r/min，0.1～0.25 s运行在1 000 r/min，在仿真试验中可调模型参数设计为：KP=4，KI=0.2，α=1，初始值为0；迭代控制器参数设定为：Γp=0.8，Γd=0.01，Γp1=0.3。图5为分别采用PI控制器和PD-ILC控制器速度响应曲线对比图。

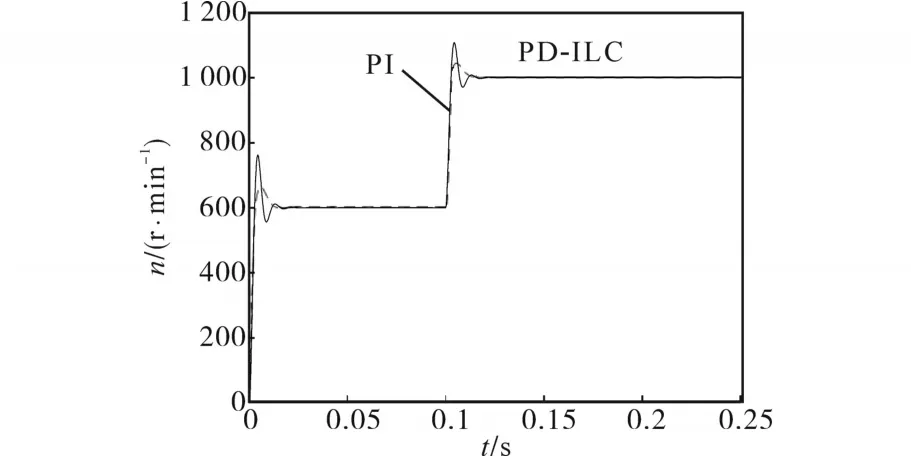
图5 速庞响库曲线对比图Fig.5 Comparison chart of speed response

4）实验平台电机参数如表1所示。

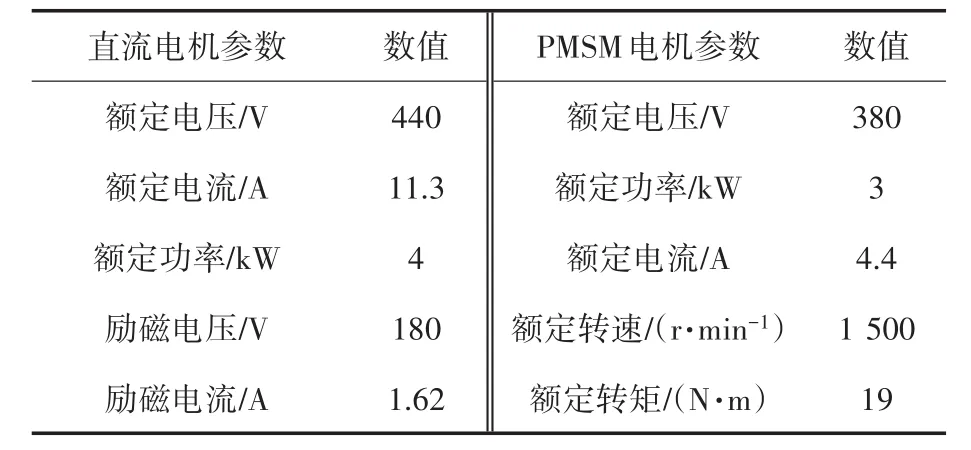
表1 实验平台电机参数Tab.1 Experimental platform motor parameters

为验证PMSM低速、中速及高速运行性能，以及对于验证PD-ILC的变速性能，进行实验验证。图6a为电机变速运行时转子转速监测曲线，分别为采用PI控制方法和PD-ILC控制方法时转速曲线。当t=1.9 s时启动电机，给定转速600 r/min；t=2.45 s时加12 N·m负载；t=2.5 s时给定转速增至900 r/min；t=2.6 s时给定转速增至1 300 r/min。图6b所示为转矩增加时电流波形图，当转矩增加时，电机相电流维持平衡且为正弦波，毛刺小，输出电能质量高。

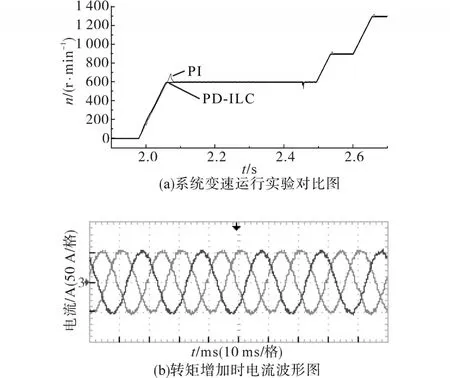
图6 系统实验图Fig.6 Diagram of system experiment

由图6可看出，PD-ILC控制策略对比PI控制策略在低、中、高速均能实现无超调给定转速跟踪，且当负载变换时，PD-ILC稳定性更好。

5 结论

本文主要对永磁同步电机无速度传感器估算准确度、调速精度问题进行了研究，研究结论如下：

1）提出了一种分数阶模型参考自适应无速度观测器，确保观测器稳定的同时，有效地解决整数阶观测精度不高的问题，提高观测器的估算准确度；

2）设计基于分数阶MARS无传感器带辅助反馈项PD-ILC控制策略，在不依赖精确PMSM数学模型情况，实现高精度的转速跟踪。