多变流器并网系统小干扰稳定性分析综述
王晓阳,赵晋斌,朱宇昕
(上海电力大学电气工程学院,上海 200090)
能源是人类社会赖以存在的物质资源,为了实现社会可持续发展,以可再生能源为代表的新能源技术越来越受到各国政府与科研人员的关注[1]。可再生能源并网技术将可再生能源通过电力电子装备变流后接入以同步机为主导的传统电力系统,从而实现可再生能源的发电与配电。该变流环节也往往决定了可再生能源并网技术的动态特性[2]。可再生能源并网系统往往采用多闭环控制,故其通常呈现为多时间尺度特性[3],并网系统的全阶数学模型也具有明显的高阶性与奇异性(运行参数分布在不同数量级上)。此外,可再生能源并网系统具有明显的弱惯性特征,当接入电网较为“薄弱”时可再生能源并网系统的稳定性能将变差,甚至发生稳定性事故[4]。基于上述背景可知,当大规模可再生能源接入“薄弱”电网时,系统将呈现为一个高阶且奇异的弱惯性系统。可再生能源并网系统的简化物理对象—多变流器的并网系统是非线性系统,很难进行直接研究。因此,在并网系统的稳态工作点的线性化模型上进行小干扰稳定性分析成为研究电力系统稳定性最主要目标,可以简化并网系统的分析复杂度,提供理论指导整个系统稳定运行。多变流器并网系统的各种小干扰稳定性分析方法在时域和频域大致划分为状态空间平均法、谐波状态空间法(harmonic state space,HSS)、阻抗模型分析法和传递函数模型分析法等。本文对上述方法的基本原理及应用范围进行梳理和总结,最后展望在未来具有价值的研究思路。
1 时域分析方法
1.1 状态空间平均法
传统的状态空间平均法是Middlebrook等人在1976年提出[5],其本质为:根据开关变换器在一个开关周期内的不同运行状态,列写状态方程;在一个开关周期内对所有变量实行加权平均,推出相应的状态空间平均方程,并在上面施加并分离小信号扰动,最终获得开关变换器的状态空间平均小信号模型。
在状态平均的意义下,高频工作下的电力电子装备可以被看成是一个微分动力学模型。故利用线性化技术,变流器并网系统可在静态工作点处近似为一个线性的平均状态空间模型[6-7]:

式中:x为系统的状态变量;A为系统的线性化状态矩阵;xp为初始状态,表征了系统的小干扰。研究状态矩阵A的特征值与特征向量可得出阻尼比、振荡频带与参与因子等重要参考信息,此即为经典的特征值分析法[8]。阻尼比可用于定量反映系统的稳定状态。振荡频带可用于分析系统的失稳频带,如次同步振荡、超同步振荡与谐波振荡等[9-10]。参与因子被用于衡量不同状态变量对不同振荡模式的贡献。故利用参与因子分析可定位到系统中的“脆弱”部分,从而实现系统失稳源的定位,这是特征值分析法在研究MGCCS小干扰稳定性时的一个重要优势[11]。其数学意义可阐述如下:设Φ为状态矩阵A右特征向量构成的矩阵,Ψ为状态矩阵A左特征向量构成的矩阵,则第i个状态变量对第k个模式的参与因子如下[8]:

式中:φik,Ψki分别为矩阵Φ与Ψ中指标为(k,i)与(i,k)的元素。
已有许多文献在状态空间平均法的特征值分析上成功实现各类电力电子装备接入电网的小干扰稳定性研究。文献[12-14]面向柔性直流输电系统,对整流侧与逆变侧的变流器建立了全阶状态空间模型,并在时域中初步确认了平均状态模型的精确度。文献[15-16]对可再生能源并网系统与柔性直流输电系统进行参与因子分析,从而进一步揭示了系统的失稳机理。然而,电力电子装备往往呈现为多时间尺度与高阶耦合特性,故建立MGCCS的平均状态空间建模将会较为复杂,分析过程耗时严重且对高阶复杂状态矩阵的特征值分析也可能导致“维数灾”等问题[17]。
由于新能源并网系统往往并联入网,而外部电网往往可通过等效变化来简化,故新能源并网系统通常可简化为树状结构。图1为一个典型的MGCCS拓扑,并网系统先将变流器聚合为n个变流器群,然后通过无源传输网络馈入到无穷大母线。

图1 典型的多变流器并网系统拓扑Fig.1 Multi-grid-connected-converter system topology
基于此,文献[18]提出一种s域节点导纳矩阵法,通过结合阻抗建模简便地获得目标特征方程。但该方法依旧要直接/间接地求解特征方程,故无法较好地降低高维MGCCS的分析复杂度。
文献[19]提出了开环模式耦合法来近似分析变流器并网系统的小干扰稳定性问题。该策略将一个变流器并网系统建模为如图2的两个开环子系统的互联反馈模型。该方法的核心思想是通过研究复杂度较低的开环模式来估计系统的闭环模式,从而简化变流器并网系统的小干扰稳定性分析。文献[20-21]推广以上方法至如图3所示的复杂多端交直流混联电力系统,建立其单输入单输出反馈闭环互联模型,并分析了多端直流系统和交流系统之间动态耦合特性。但该判据是系统失稳的必要条件而非充分条件,只能评估系统的失稳风险,无法对系统稳定性进行直接判断。

图2 变流器并网系统的康环子系统分解Fig.2 Open-loop subsystem decomposition of converter grid-connected system

图3 多端交直流混联电力系统Fig.3 Multi-terminal AC/DC hybrid power system
但使用状态空间平均法对MGCCS分析存在一些问题:并网变流器和电网的全部参数确定才能建立起一致的状态空间模型,但是MGCCS的组成单元和控制参数可能随时变化,使得进行系统分析变得繁琐复杂;高阶数学模型不能直观表现其物理意义,在系统动态稳定问题分析上复杂度比较高,不利于迅速辨认电网失去稳定性的主因。
1.2 谐波状态空间法
虽然状态平均可将电力电子装备从一个非连续非自治的动力系统在开关时间尺度上近似为一个光滑自治动力系统,但却很难体现时域上系统的μs级电磁暂态特性,因此文献[22-23]基于多谐波线性化提出了谐波状态空间法。相较传统的平均建模,该模型在物理上可更深刻地反映电力电子开关的动力学特性与高阶谐波交互特性。
定义线性周期时变系统如下:

式中:A(t),B(t)为周期性的时变量;x(t),u(t)分别为系统的状态变量和输入变量。
对于开关变换器,其稳态呈现出周期性时变的特征,因此可将其视为一个非线性时间周期模块。针对线性时间周期系统的研究提出了谐波状态空间的概念。HSS模型中各频次分量信号可用傅里叶变换从时域变换为频域进行分析,为探究系统的动态性能,用指数调制周期函数去描述信号,具体如下:

将式(4)代入状态方程与输出方程,可以推出包含所有谐波分量的谐波状态空间方程。
文献[24-25]进一步将谐波状态建模推广至各类电力电子装备,如高压直流输电(high voltage direct current,HVDC)系统与模块化多电平变换器(modular multilevel converter,MMC)系统等。此外,为将HSS应用于系统稳定性分析,文献[26]将HSS与阻抗分析相结合进一步提出基于HSS的小干扰稳定性分析方法,达成了SGCCS的稳定性分析和控制器综合。
尽管HSS建模实现了变流系统的精细化建模,但HSS在理论上是一个无穷维状态空间模型,在工程应用中应进行截断计算,而这尚未存在相应的指导理论。将其应用于MGCCS时,该模型将会十分复杂,从而导致大量数值稳定性问题。此外,在线性化分析中,该模型需要多谐波意义下的静态工作点,而这无法通过传统的潮流计算直接获得。故基于HSS的时域分析更加适用于装备间的谐波交互研究而非大系统的稳定性分析。
2 频域分析法
2.1 阻抗分析法
对变流器并网系统进行阻抗分析是一种使用最广泛的稳定性分析策略。该方法首先建立变流子系统和电网子系统的等效阻抗模型,然后用频域的Nyquist或广义Nyquist判据对阻抗比进行分析。
2.1.1 阻抗建模方法
通过建立阻抗/导纳模型对小干扰稳定性进行频域分析是另一种基于平均模型方法。在变流器并网系统的研究上,该方法最早被应用于拓扑较为简单的SGCCS中。其基本逻辑是将变流器并网系统视为两个源荷子系统,并将源荷系统的控制结构和参数特征分别按阻抗/导纳模型建模为等效戴维南/诺顿电路,从而将原系统的小干扰稳定性问题归纳到s域电路进行分析[27-28],如图4a所示。在阻抗/导纳模型中源荷子系统任何一方组合单元的结构和参数的变化对彼此没有影响。

图4 阻抗分析的原理分析Fig.4 Principle analysis of impedance analysis
利用等效戴维南/诺顿电路图可以得到系统的传递函数表达式:

式中:ΔIg为并网电流;E1/2为一维或二维单位矩阵,取决是否考虑三相并网系统的阻抗耦合特性;Yvsc为变流器的导纳模型;Zg为接入电网的阻抗模型;Ip,Up分别为系统小干扰等效出来的电流源、电压源。
显然上述方程对应了图4b的控制框图,在恰当的参数下一般可认为Ip,Up,Yvsc与Zg是稳定的,故图4b是具有稳定输入的开环稳定系统。由线性系统理论可知图4b系统的稳定性可由开环函数YvscZg决定,一般定义该开环函数为阻抗比函数L,即

如果SGCCS是一个一维系统,对一维阻抗比L应用经典频域法,如Bode图与Nyquist判据等即可实现系统小干扰稳定性的分析与综合,这是阻抗分析方法的基本思路。通过阻抗模型建模流程中参考坐标系的区别,广泛使用的阻抗建模策略为:基于d-q旋转坐标阻抗建模与基于正负序坐标的谐波线性化建模。
但在d-q阻抗与正负序阻抗建模下传统并网变流器存在着d-q耦合效应或频率耦合效应,即SGCCS表现为双输入双输出特性[29-31]。所以完整的小干扰稳定性分析常需要用到形式更为复杂的现代频域法,比如广义Nyquist判据与奇异值分析等[32-33]。
为此,文献[34]提出一种极坐标阻抗,从而获得了单位功率因数下SGCCS的一维阻抗模型,通过严格数学变换将变流器并网系统从多输入多输出(multiple input multiple output,MIMO)问题转为单输入单输出(single input single output,SISO)问题,再利用电路谐振对系统振荡进行解释,最后使用Nyquist曲线即可判断系统稳定性。在全局极坐标系下建立变流器和电网阻抗模型可表示为

但该极坐标解耦方法目前仅仅适用于单位功率因数逆变器。文献[35]则提出一种对称导纳模型,可以将并网系统用一个互易二端口电路表示,通过矩阵变化获得了SGCCS的等效一维阻抗模型来探讨系统的振荡机理。但该解耦方法目前仅仅适用于不考虑变流器外环动态的情形。为此文献[36]建立了变流器外环控制器动态影响下的并网系统极坐标阻抗模型与复电路,推出极坐标广义阻抗判据及等效SISO系统,并解释此判据本质即是对端口电压相位主导回路的谐振分析。并继续研究了外环控制器、锁相环动态对并网系统稳定性的影响。
但上述方法都尚未推广至MGCCS。所以文献[37-40]提出MGCCS的一种在同步旋转坐标系下的阻抗建模策略。并在已知系统振荡路径的背景下,利用振荡路径的阻抗聚合,可将系统的特征方程表示为
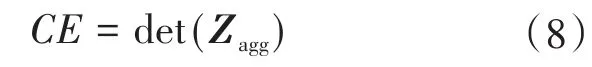
式中:CE为系统特征方程;Zagg为振荡路径下的聚合阻抗。
利用该方程的频域特性可以快速得到系统阻尼与振荡频率等稳定性信息,并且得到稳定性量化分析方法,建立聚合阻抗判据。文献[41-43]从电网的“薄弱”特性评估提出了广义短路比的概念,从而将MGCCS解耦为若干个等值的SGCCS。基于该方法MGCCS的稳定性分析可被简化为对SGCCS进行分析,但该方法的系统必须有一定的对称性。
文献[44]将MGCCS拓扑建模为一个开环稳定的MIMO负反馈模型,如图5所示。MGCCS被分为由变流器群组成的有源子系统和由传输网络与无穷大母线组成的无源子系统,建立一个以TYST-1ZL为开环函数的负反馈模型,如下式:


图5 MGCCS的负反馈模型Fig.5 The negative feedback model of MGCCS
ZL为该端口网络的阻抗网络矩阵,YS=diag(Ys1,…,Ysn),Ysk是usk到isk的传递函数,T为坐标变换矩阵。定义MGCCS的广义阻抗比LM为

但是树状结构的阻抗模型很难用于更加复杂的多端交直流系统。
2.1.2 阻抗稳定性分析
阻抗稳定性判据是变流器与电网互联系统稳定性量化分析重要理论基础,并提供了并网逆变器结构与环路参数设计方案。本节归纳了适用于SGCCS的稳定性判据,并拓展到MGCCS领域。
在研究三相并网变流器与电网交互系统的稳定性时,采用d-q轴阻抗建模方法得到的交互系统为MIMO。所以通过阻抗比函数L能否符合广义Nyquist判据来确认三相并网变流器与电网的稳定状态。但是由于广义Nyquist判据拥有比较高的复杂度,因此广泛借助d-q耦合效应推导出一些复杂度较低的判据,其可以分成奇异值判据、D通道判据和范数判据。
在此基础上,文献[45]讨论了四种基于SGCCS的范数类判据,建立了相较广义Nyquist判据更为简洁的G-Sum范数判据,并证明其保守性的优势。尽管该判据一定程度上实现了源荷解耦与复杂度降低,但判据是充分判据具有一定的保守性。G-Sum范数判据:若任意频率ω满足

则交互系统是稳定的。
文献[46]在序阻抗的基础上利用阻抗比矩阵的特征值估计建立了一个复杂与保守性较低的禁止域判据。判据形式如图6所示,灰色部分为轨迹禁止域,当Nyquist轨迹涉及到灰色部分时,表明系统的稳定裕度不足。但当满足判据的情况下,相位、幅值裕度PM,GM有如下估计:


图6 基于禁止域的等价康环函数判据Fig.6 Equivalent open-loop function criterion for forbidden fields
相较SGCCS,MGCCS更是典型的高阶MIMO系统,其分析过程将更为复杂。一般来说,为探究多变量线性系统的稳定性问题,需要求解特征方程特征根或者使用广义Nyquist判据。但是由于特征方程判据的复杂度过高,多变量线性系统理论中的广义Nyquist判据可被应用于MGCCS的小干扰稳定性,判据可被归纳如下[47]:
广义Nyquist判据:MGCCS是小干扰稳定,当且仅当LM的特征值轨迹包围(-1,0)的逆时针圈数N+等于其包围(-1,0)的顺时针圈数N-。LM是阶数为2n的非对角矩阵。但是如果开环传递函数矩阵高于4阶情况下广义Nyquist判据已无法代数解。故使用广义Nyquist判据研究MGCCS的小干扰稳定性问题将更为困难。
为了在经典频域内分析稳定性问题,文献[48]提出一个等价开环函数判据,并定义了一个等价开环函数为
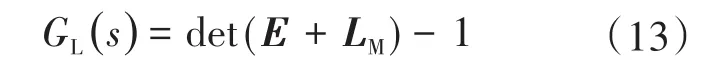
上述开环函数表示了一个以1为前向通道,GL(s)为负反馈通道的SISO系统,如图7所示。
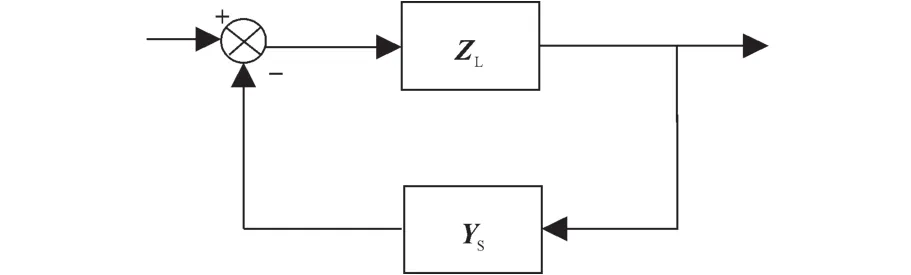
图7 等效SISO系统Fig.7 Equivalent SISO system
等价开环函数判据:MGCCS是小干扰稳定的,当且仅当GL(s)的Nyquist轨迹不包围临界点。广义Nyquist判据与此判据的复杂度相当,但Nyquist轨迹的形式相对简洁,且方便进行直观的稳定裕度设计。
为了继续降低判据复杂度,文献[44]提出GSum范数的复杂度是远低于广义Nyquist判据,故其可以适用于更大规模的MGCCS稳定性分析,但是保守性略高。所以基于矩阵特征值的估计理论,给出了MGCCS的特征值域判据,可将稳定性条件总结为一个代数函数下界值的大小。
特征值域判据的几何意义如图8所示,其代数意义为:若对任意频率ω满足f(ω)>0,那么对应MGCCS满足小干扰稳定条件。若进一步有f(ω)>r,相位幅值裕度PM,GM满足下式:


图8 特征值域判据Fig.8 The eigenrange criterion
由于频域判据计算过程不需要获得具体的解析表达式,只涉及各个有源节点与无源网络的频域特性,此判据有一定处理高阶MGCCS的潜力。
不同阻抗稳定性判据的比较分析如表1所示。由于电力电子化系统往往涉及多交直流异构变流器多异地接入,相较现有文献讨论的多变流器并网阻抗模型较为简单,尚无法完全表征电力电子化电力系统的动力学特性。故对于更为复杂的电力电子化系统的小干扰稳定性阻抗建模依旧等待进一步研究,如交直流混联电力系统与交直流微电网。

表1 不同判据的比较分析Tab.1 Comparative analysis of different criteria
阻抗分析法可以有效表现两个子系统对系统稳定性的影响,但在MGCCS中只能使多机中一部分合并,然后对两个子系统开始稳定性分析。所以这难以表现不同装备本身各自在系统稳定性上造成的影响。
2.2 传递函数分析法
为使变流器并网系统从MIMO系统简化为SISO系统,文献[49-51]提出一种传递函数模型,在将SGCCS的各部分模型使用线性化进行处理后,SGCCS被等效为一阶传递函数模型,并通过传统频域法中的Nyquist稳定判据或Bode图上的稳定判据即可实现对SGCCS的分析与综合。
但在MGCCS中,多种类型装备间的耦合作用与系统稳定性的关系需要精细衡量,并以此来控制系统的整体稳定性。基于此,文献[52]基于自稳性和致稳性分析思路提出一种路径级数展开法。该方法可以精确描述多装备耦合相互作用,建立基于装备—网络的等效传递函数模型。对比于现有频域分析方法大部分用于衡量两个子系统对系统稳定性的影响,该方法可以精细化溯源,使系统内复杂耦合路径的形成过程可以直观描述并且解析化频域分析和简化系统的分析过程。但是传递函数模型所需数据巨大,建模过程程序复杂,计算量也偏大。
3 结论
本文对现有多变流器并网系统建模与稳定性分析的方法进行了全面的归纳和总结,有效地简化了交互系统稳定性分析的复杂度,对电力电子化电力系统的稳定性研究有着一定借鉴意义。对MGCSS这种复杂结构电力系统稳定性的研究来说,未来还需从对如下工作开展研究:
1)电力电子化电力系统除受电力电子装备影响外,可再生能源的间歇特性与负载的频繁切投也对系统的稳定性有着深刻影响。这往往将导致系统发生大干扰不稳定,而由于电力电子化电力系统的高阶非线性,故该暂态稳定性问题逐渐凸显出来,并且十分值得下一阶段研究。
2)除去稳定性判断外,稳定性的优化与设计更是一个工程实际问题。而由于电力电子化电力系统的多接入特性,其数学模型往往十分复杂,故如何在多异构电力电子装备多接入背景下对电力系统的稳定性进行优化与设计同样也是值得挑战的。

