同步电动机调速系统参数优化研究

张成，韩存 ，任巍，赵晋雷，张啸，张旭东

（1.天津电气科学研究院有限公司，天津 300180；2.中国宝武太钢不锈冷轧厂，山西 太原 030003）

电励磁同步电动机具有功率因数高、效率高和过载能力强等优点[1]，目前已在各种大功率传动场合应用广泛，如大功率水泵、空气压缩机、轧机主传动系统等。目前矢量控制是电励磁同步电动机的主流控制方法之一，通过坐标变换，将定子电流分解为励磁电流和转矩电流分量，然后对其分别进行控制，从而实现对磁链和转矩的控制[2-4]。随着人工智能技术的发展，专家系统、模糊控制、自适应控制、辨识理论、人工神经网络纷纷应用于电机控制领域，并取得了一定的成果[5-8]。

在工业自动化中，由于同步电机调速系统中PI调节器的参数对调试人员的经验依赖性较高，调试人员很难根据控制系统的响应要求迅速整定出调节器参数。

针对上述问题，本文利用混沌粒子群算法对PI调节器参数进行优化。通过一种混沌映射—动态整数Tent映射[9]构造了一种伪随机序列生成方法，设计了一种粒子群算法的目标函数，能够直观地反映控制系统的阶跃响应性能指标，最后使系统达到最优效果。

1 同步电动机交直交变频调速系统

同步电动机交直交变频调速系统主要包括磁链调节、电流调节和转速调节。本文对磁链调节和电流调节做简单介绍。

1.1 磁链调节器

同步电动机磁链调节器由两部分组成[10]：一部分为比例调节器，作为定子电流的磁链调节外环，这部分调节较快，只在动态起作用；另一部分采用比例积分调节器，作为励磁电流环的外调节环，这部分调节较慢，但可消除静差。

由于励磁绕组轴线位于d轴且阻尼绕组电阻rDd很小，忽略后等效电感为

式中：Le为d轴等效电感；Leσ为定子漏感；Lhd为d轴主电感；LDdσ为d轴阻尼绕组漏感。

在磁链调节器结构中，励磁电流调节环和磁链反馈滤波时间常数等可以用一个等效惯性环节代替，时间常数为TΣe。通过励磁电流环的磁链调节环传递函数框图如图1所示。

图1 通过励磁电流环的磁链调节环传递函数框图1Fig.1 Transfer function diagram1 of flux regulating ring through excitation current ring

图1中，Kμe为比例系数，，ΨΜΝ为额定磁链，为空载励磁电流；TΨe为磁链调节器积分时间常数；KΨe为磁链调节器比例系数。d轴阻尼绕组等效时间常数TDd0计算方法为

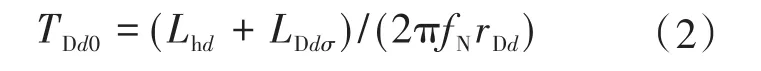
式中：fN为定子额定频率。

在磁链调节器结构中，定子电流磁化分量调节环可以用一个等效惯性环节代替，时间常数为TΣi。通过定子电流环的磁链调节传递函数框图如图2所示。

图2 通过定子电流环的磁链调节传递函数框图Fig.2 Transfer function block diagram of flux regulation through stator current loop

图2中，TΣi为电流调节环等效时间常数；KΨs为比例系数，为折算到定子侧的空载励磁电流。q轴阻尼绕组等效时间常数TDq0为

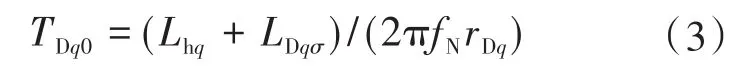
1.2 电流调节器

交流同步电机调速系统的电流控制包括定子电流控制和转子激磁电流控制。交直交PWM变频调速系统的定子电流控制由磁场定向MT坐标系的直流电流控制构成[11]。

为了分析方便，取负序电感L2作为电流通路的电感，可以推出MT轴电流控制系统的传递函数：

式中：ism为定子电流磁场分量；Rs为定子绕组电阻；L2为负序电感；usm为M轴定子电压；Lsl为定子漏感；ωs为转速；ist为定子电流转矩分量；ust为T轴定子电压；Ψδ为磁通量。

由于稳态电压方程为

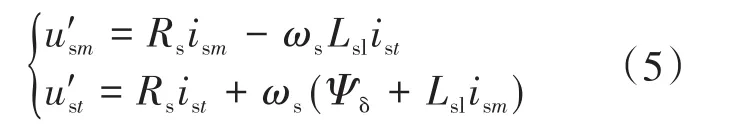
电流控制系统的传递函数可以写为

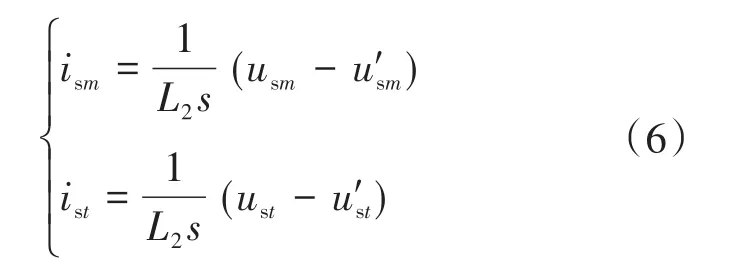
如果考虑电压前馈环节，把电压稳态方程构造出来，令电压前馈计算环节等于电压稳态方程，使，如下式：

M，T轴电流环完全解耦独立，消除了定子漏抗和感应电势的交叉耦合，如图3所示。

图3 电流控制系统的传递函数Fig.3 Transfer function of current control system

由于加入电压前馈环节后，M，T轴电流控制完全独立，电流控制的对象为负序电感L2的积分环节，因此，比例积分调节器Gi(s)将对积分环节1/(L2s)进行工程设计。

2 混沌粒子群算法

2.1 粒子群算法

粒子群算法由Kennedy和Eberhart提出，是一种进化算法，其基本思想是通过个体间的信息交换与共享来寻找最优解。算法中的粒子从随机位置出发，通过迭代、更新操作，搜索目标函数的最优解。

粒子群算法的核心公式包括速度更新公式和位置更新公式。

速度更新公式如下：

式中：i为迭代次数；vi为第i代粒子群的速度集；ω为惯性权重因子；c1，c2分别为个体学习因子和社会学习因子；rand为（0，1）间的随机数；pbest为个体粒子最优位置集；gbest为所有粒子最优位置；xi为第i代粒子位置集。

位置更新公式如下：

粒子群算法流程图如图4所示。

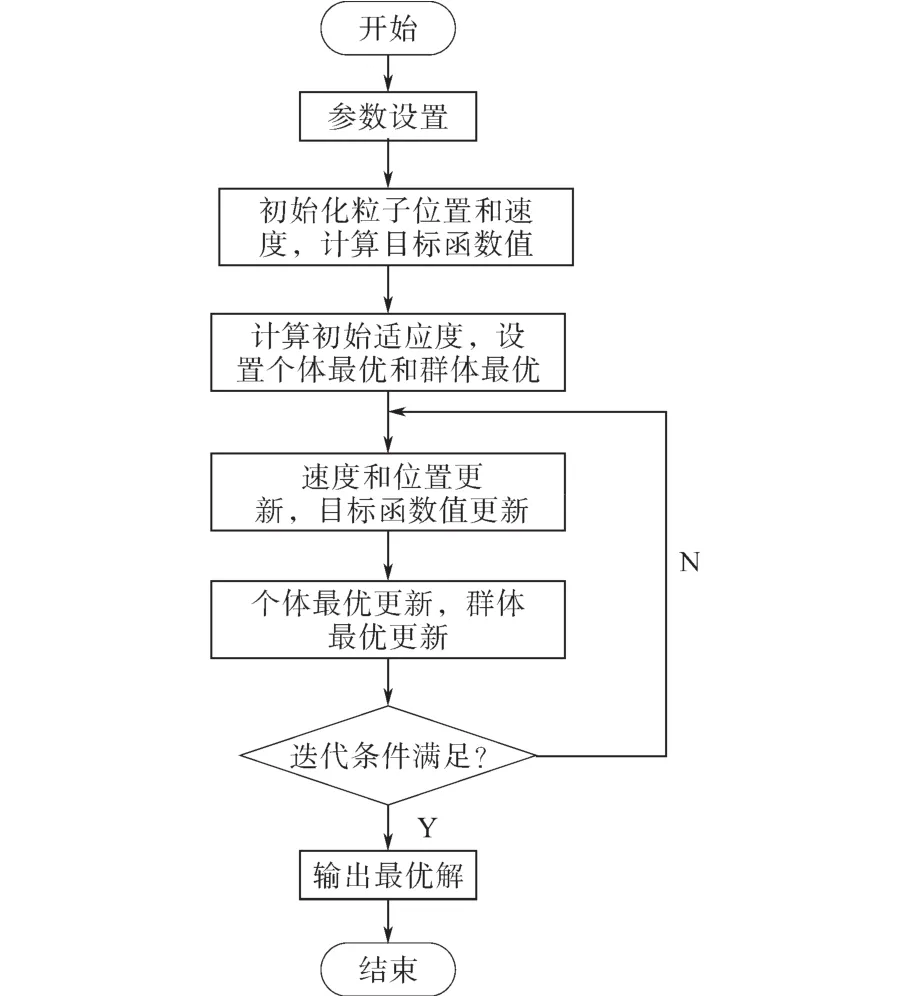
图4 粒子群算法流程图Fig.4 Flow chart of particle swarm optimization

2.2 随机数生成算法

对于粒子群算法的初始位置及速度，可以采用混沌映射方法获得。混沌映射具有非线性、遍历性、随机性以及对初值的敏感性等优良特性，在生成伪随机序列方面应用广泛。对于粒子群算法，混沌映射的引入能够有效避免算法陷入局部最优，增强算法寻优能力。常见的混沌映射有Logistic映射、Tent映射、Henon映射等。

常规混沌映射涉及的范围均为浮点型数据，从存储、运算效率、资源占用等方面看，整数运算更适合计算机系统。因此本文采用一种动态整数Tent映射来生成伪随机序列。

动态整数Tent映射描述为

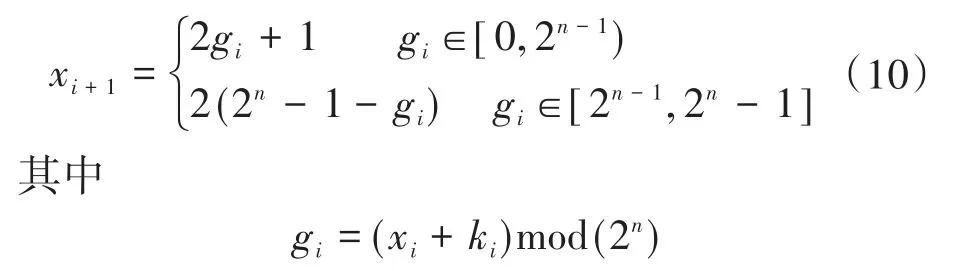
式中：n为x取值范围内最大整数的二进制位数；ki为整数Tent映射的动态参量。

利用动态整数Tent映射构造的随机数生成算法为：

Step 1：确定x取值范围，即确定整数二进制位数n；

Step 2：取当前时间，如2021-03-14 20∶13∶12，按自右向左的顺序依次取每个有效数字对应字符的ASCII码，即timearray=[50，49，51，49，48，50，52，49，51，48，49，50，48，50]；

Step 3：取ki=i，以timearray第0个元素为初值，利用式（10）进行迭代，每迭代10次依次加入timearray中的一个元素，如下式所示：

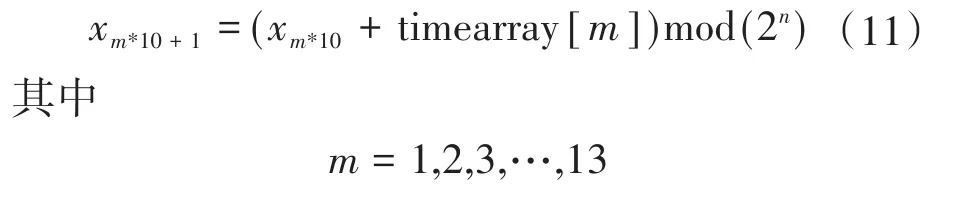
迭代10次后结果为x10；然后进行运算x11=(x10+timearray[1])mod(2n)，利用式（10）迭代10次后结果为x20；再进行运算x21=(x20+timearray[2])mod(2n)，利用式（10）迭代10次，以此类推。将timearray[13]加入运算后得到x131，再利用式（10）迭代50次，得到最终结果x181；

Step 4：取rand=x181/2n，得到（0，1）区间随机数。

2.3 目标函数设计

常用的目标函数包括绝对误差积分（IAE）指标、平方误差积分（ISE）指标、时间乘绝对误差积分（ITAE）指标。经过实验发现，以上指标均不适用于工程问题，因为上述指标均不能从超调量、调节时间等指标方面反映控制效果。

工程上同步电机PI调节器的参数优化问题实际上是一个多目标优化问题，即搜索一对PI调节器系数(Kp,Ki)使目标函数最小。目标函数应是与系统阶跃响应的上升时间、调节时间、超调量等指标相关的函数。

多目标优化问题一般有两种解决方案：一是将多目标优化问题转化为单目标优化问题，如将多个目标函数加权相加；二是利用多目标粒子群优化算法，传统的多目标粒子群优化算法较为复杂，且得到的是一个Pareto解集，其结果是一种兼顾多目标要求的解集。

本文采用第一种方案，将多目标优化问题转化为单目标优化问题，设计一种目标函数，能够满足工程上的PI调节器参数优化需求，使系统效果最优。

设控制系统阶跃响应期望上升时间为ex_tr，期望调节时间为ex_ts，期望超调量为ex_δ，则目标函数定义为

式中：tr为实际上升时间；ts为实际调节时间；δ为实际超调量。tr，ts，δ三个变量均受到自变量Kp,Ki的影响，实际上式（12）所示的目标函数是以Kp,Ki为自变量、f为因变量的函数，其解析式较复杂，实际应用时根据一对(Kp,Ki)的实际响应曲线得到tr，ts，δ，进而计算出目标函数值。

3 仿真结果

3.1 磁链调节

以图1为例进行优化仿真。图1中，取

将图1进行等效变换，如图5所示。

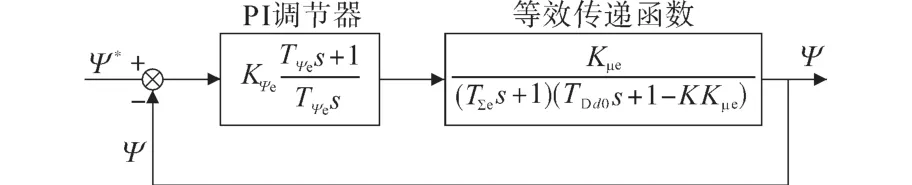
图5 通过励磁电流环的磁链调节环传递函数框图2Fig.5 Transfer function diagram 2 of flux regulating ring through excitation current ring

取磁链调节仿真参数如下：T∑e=0.017s，Kμe=3.2，TDd0=0.029 s，K=0.2。设置粒子群算法参数如下：个体学习因子c1=2，社会学习因子c2=2，惯性权重因子ω=0.8，迭代次数100，粒子群规模40，速度限幅[-1，1]，粒子位置限幅[0，10]。随机数生成算法参数设置如下：整数二进制位数n=10，迭代初值=1。

采用上述参数进行仿真，得到粒子群算法迭代过程如图6所示。

图6 粒子群寻优过程（磁链调节器）Fig.6 Particle swarm optimization process（flux regulator）

磁链调节器参数优化结果如表1所示，同时表中也给出了对称最佳法得到的PI调节器参数。

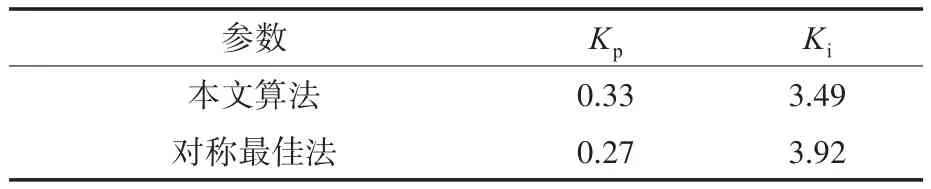
表1 磁链调节器参数结果Tab.1 Flux regulator parameter results

对于图5给出的控制框图，将表中磁链调节器参数代入，得到两种方法的系统阶跃响应结果，如图7所示。同时得到两种算法阶跃响应的三种性能指标如表2所示。可以看出，本文采用的混沌粒子群优化算法整定出来的磁链调节器参数在上升时间、调节时间、超调量等阶跃响应指标上均优于传统的对称最佳算法。

表2 阶跃响应性能指标（磁链调节器）Tab.2 Step response performance index（flux regulator）

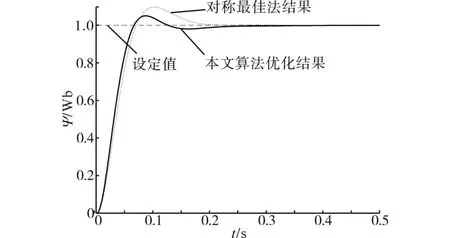
图7 磁链调节阶跃响库仿真结果Fig.7 Simulation results of step response of flux chain regulation

3.2 电流调节

对图3解耦的电流控制系统进行仿真，混沌粒子群算法参数设置同3.1节，负序电感L2取值0.012，以上述参数进行仿真，得到粒子群算法迭代过程如图8所示。

PI调节器参数优化结果如表3所示，同时表中也给出了经验整定得到的PI调节器参数。

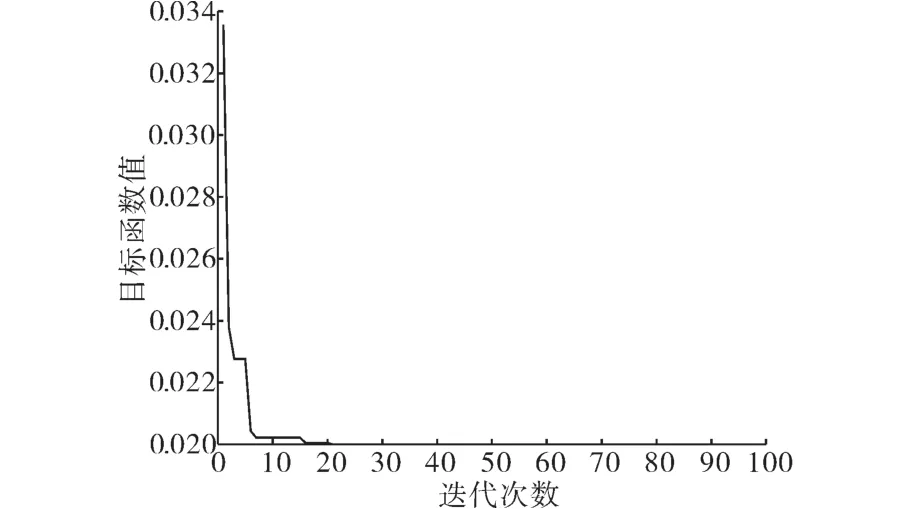
图8 粒子群寻优过程（电流调节器）Fig.8 Particle swarm optimization process（current regulator）

表3 电流调节器参数结果Tab.3 Current regulator parameter results

对于图3给出的控制框图，将表中电流调节器参数代入，得到两种方法的系统阶跃响应结果，如图9所示。同时得到两种算法阶跃响应的三种性能指标如表4所示。可以看出，本文采用的混沌粒子群优化算法优化后的系统响应结果与经验整定结果差别不明显，但依旧略优于后者。

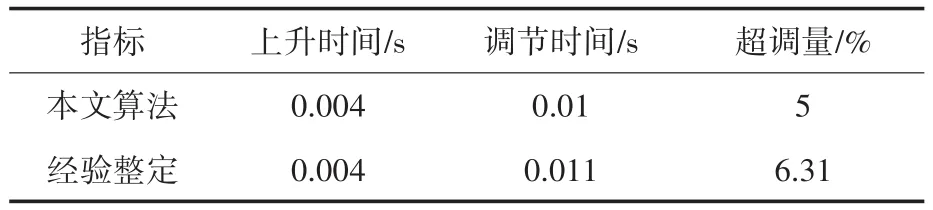
表4 阶跃响应性能指标（电流调节器）Tab.4 Step response performance index（current regulator）

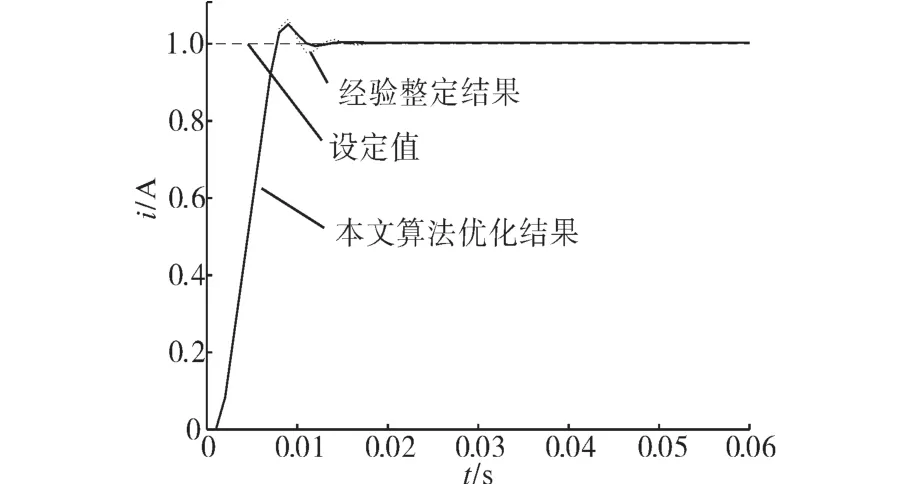
图9 电流调节阶跃响库仿真结果Fig.9 Simulation results of step response of current regulation

4 现场运行结果

实际应用中，首先根据生产线工艺要求，提出系统期望的上升时间、调节时间及超调量，然后根据系统的传递函数进行优化。将本文算法应用到太钢不锈钢冷轧厂森吉米尔轧机主传动调速系统，图10为同步电机现场实际运行波形图，图中磁通调节器及电流调节器的参数如表5所示。

表5 磁通调节器及电流调节器参数设置Tab.5 Parameter setting of flux regulator and current regulator

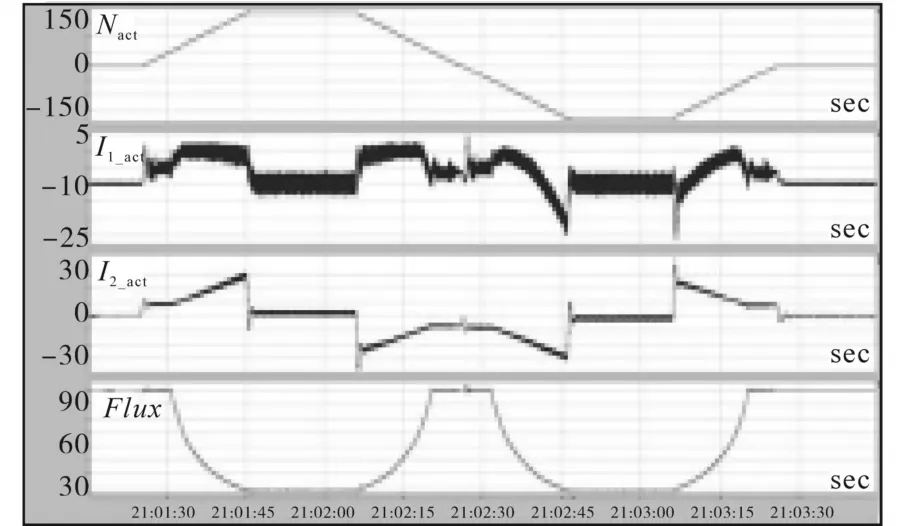
图10 实际运行结果图Fig.10 Actual operation results

图10中，Nact为速度实际值，I1_act为定子电流的磁化分量，I2_act为定子电流的转矩分量，Flux为磁通。由图10可以看出，经过本算法优化的PI调节器在实际应用中能够满足控制系统的要求，能够应用于实际生产中。

5 结论

本文利用混沌粒子群算法对同步电机交直交变频调速系统中的PI调节器参数进行优化，提出了一种基于整数Tent映射的随机数生成算法，针对控制系统的阶跃响应，设计了一种直观的、适用于工程的目标函数。本算法对系统进行离线优化，对系统的软硬件环境没有特殊要求，实现方便，通用性强。通过对比仿真与现场应用，说明了算法的优越性与有效性。