基于康托尔分形微通道流动与传热的模拟

李伟浩,陈缤,徐阳,关欣

上海理工大学 能源与动力工程学院,上海 200093

1 引言

电子元器件工作时间过长产生的热效应会使元器件的工作温度升高,导致高温区域出现热应力,造成电子元器件性能衰减,故高集成度高功率的电子器件要求更高效的换热技术,微通道换热技术因其结构紧凑、换热效率高的特点,成为小空间、高热流密度电子器件散热的有效解决方式之一.

电子产品的微通道换热技术始于20世纪80年代初,D.B.Tuckerman与R.F.Pease[1]首先提出了微通道换热技术的构想,并以硅为材料制造出了微通道热沉,进行了实验研究.刘赵淼[2]等通过数值模拟研究了几何参数(包括水力直径、通道长度、进口高宽比等)对不同结构微通道内液体流动与传热的影响,得出了几何参数对泊肃叶数和努塞尔数的影响趋势.邓梓龙[3-4]等对微通道粗糙表面进行了研究,建立了气体在粗糙微通道中流动的理论模型,采用格子Boltzmann方法模拟研究了表面粗糙对微尺度气体流动的影响,比较了粗糙和光滑微通道内气体流动特性.吴慧英[5-6]等对微通道的结构形状进行了实验研究.当微通道形状为梯形结构时对比发现:层流状态下,几何参数和表面摩擦系数对通道内努塞尔数影响很大,且随着雷诺数的增大趋势明显.当通道形状为正弦波纹形时,相对于矩形通道,进出口压差明显增大,且增加幅度与波纹微通道两侧壁的相位差和周期有关.邓大祥[7-9]等对一种新型的周期性扩张约束微通道(PECM)散热器进行了试验和数值模拟,并与矩形微通道进行了对比,研究发现这种新型PECM散热器冷却效率更优.其团队也对微通道内加入微针肋后的对流传热和压降性能进行了研究.吴泽阳[10]等设计了一种基于康托分形结构的新型低压电渗微混频器,研究了分形电极对长度对混合性能的影响、电极位置的影响以及分形电极组间距对混合效率的影响.Ghule K[11]等研究了四种不同的截面(即矩形、圆形、切口矩形和切口圆形)的波纹微通道,采用有限体积法对这些通道进行了三维稳态数值传热分析.结果表明,由于流体混合的增强,传热系数随波纹振幅的增大而增大.Sahara A M[12]等模拟了由进口和出口矩形管汇组成的平行微通道结构,研究了通道间的流动分布,结果显示:当进出口管汇面积减少50%时,压降增加约5%.而流形管进出口面积对流速和流体温度分布的影响不明显.Munib Q A[13]等人对具有混合矩形表面粗糙度结构的微通道进行了数值分析.结果表明,具有规则表面粗糙度结构的微通道比各自具有混合表面粗糙度的微通道热阻高约14%,结构表面粗糙度与合适的配置可以是一种创新的方式以提高电子冷却散热.Fakhrodin L[14]等通过考虑微通道壁面粗糙度的不同以及几何形状和流动条件的变化,研究微通道内的摩擦和压降的变化,确定了五种粗糙元效应的差异.Jafari R[15]等通过实验研究了表面粗糙度对微通道蒸发器水动力和热性能的影响.考虑微通道壁面粗糙度的影响,建立了一种新的关联关系来预测微通道中R134a沸腾的传热系数.Sadaghiani A K[16]等人利用数值模拟方法研究了粗糙元结构及其分布规律对不同形状微通道的影响.结果表明:针翅形状的换热效果随着表面粗糙度的增大呈现减小趋势.Siddharth R[17]通过数值模拟的方法,研究了不同粗糙度高度和雷诺数下压降和摩擦因数的变化规律.结果表明,偏置模式比标准模式具有更高的压降和泵浦功率,摩擦因数也较高.

根据以上文献发现,目前国内外关于微通道的研究主要是结构优化[2,5-12]或改变通道内环境[3-4,13-17].从换热器的结构优化上来讲,采用分形结构的微通道,能有效地降低压降,减小泵功;从单个换热元件上讲,加入凹槽结构能有效地加大固液接触表面积,从而强化换热,但是相较于光滑通道,压降明显提升,需要额外的能耗来弥补泵功.因此,寻找一种既能强化换热又能尽量降低压降的换热单元结构迫在眉睫.本文主要是根据目前的研究热点提出了一种带有康托尔分形凹槽的微通道,并研究其流动和传热特性.

2 微通道形状和尺寸对流动换热影响

2.1 微通道截面形状对流动换热的影响

本文首先对微通道的截面形状进行研究,为后文的研究选择最优进出口形状.图1为微通道截面简图.设置了四组对照组N1～N4进行研究,其结构参数见表1.其中通过改变Wb/Wt的值来改变截面形状:当Wb/Wt=0时,此时截面形状为三角形;当Wb/Wt=1时,此时截面为矩形;当0＜Wb/Wt＜1时,此时截面为梯形.微通道热沉的固体材料选用铜材料,通道内液体采用去离子水.

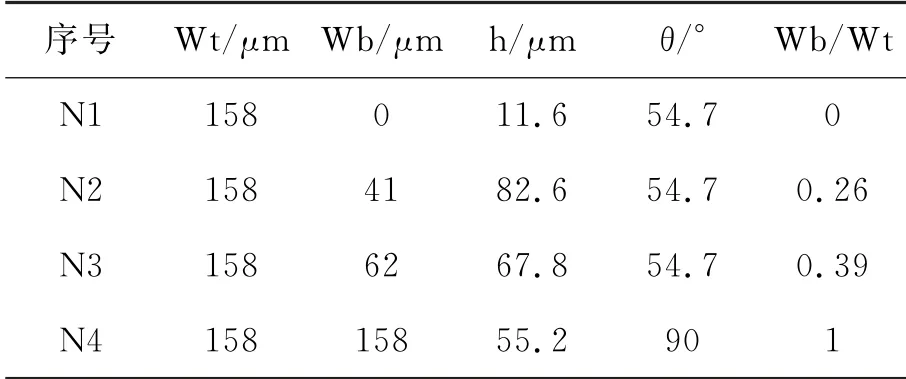
表1 单个微通道的尺寸

图1 微通道截面简图

本文对N1～N4四组微通道内液体流动与传热特性进行模拟研究.为简化分析过程,假设液体为常物性,处于层流稳态,忽略重力和黏性耗散的影响,只关注微通道底部施加的恒定热流,忽略其它热源作用.采用SIMPLE算法和有限差分法来进行求解,以N4的矩形通道为例进行网格无关性验证,结果表明,网格数量为734550的模拟结果其压降的相对误差与基底底面平均温度的相对误差均小于1%,综合计算精度与计算周期的最优化,本文将微通道模型的网格数量定为734550.

图2为相同Re数范围内,N3组换热Nu数计算值与文献的实验值[5]的对比.

图2 N3组数值计算Nu数与实验数据[5]的对照

根据图2可知,在一定的Re数范围内,数值模拟得到的数据与文献中的实验数据能够很好的吻合,因此也证明了本文所采用模型的准确性.

图3为N1～N4四组模型截面平均努塞尔数Nux沿流动方向(x方向)上的发展趋势.图3表明:(1)从整体上看,N1-N4组都表现为入口处截面平均Nux数出现最大值,然后急剧下降,最终缓慢趋于稳定.这是由于入口处边界层迅速增厚导致,不同界面边界层迅速增厚都发生在前1 mm处.这就说明流体在流动过程中,沿流动x方向上的对流换热能力在逐步减弱;(2)对比N2组和N3组,虽然截面形状相同,但是就水力直径而言:N2＞N3,整体上平均Nux数为:N3＞N2,也就是说换热强度:N3＞N2,因此,对于相同进出口截面形状的微通道,水力直径越小,湿周越大,固液接触换热面积越大,换热效果越好;(3)在相同水力直径下,整体上平均Nux数为:N4＞N1＞N2,也就是说水力直径一定的情况下,相比于梯形和三角形微通道,矩形微通道的换热效果最好.因此本文选择换热效果最优的矩形微通道作为研究对象.

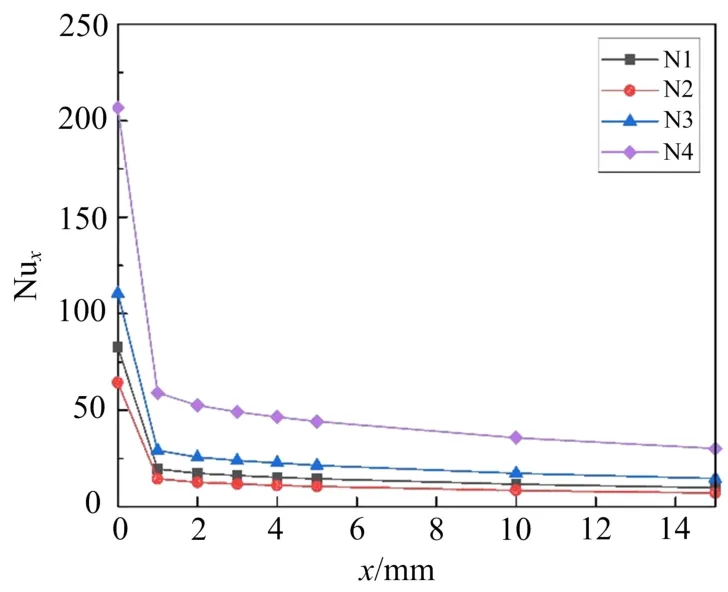
图3 截面平均Nu x数沿流动方向的发展趋势

2.2 进出口截面尺寸对流动换热的影响

本文主要研究矩形微通道的进出口截面尺寸的影响,即矩形进出口宽高之比对微通道换热性能的影响.图4为矩形微通道单元进出口截面示意图.

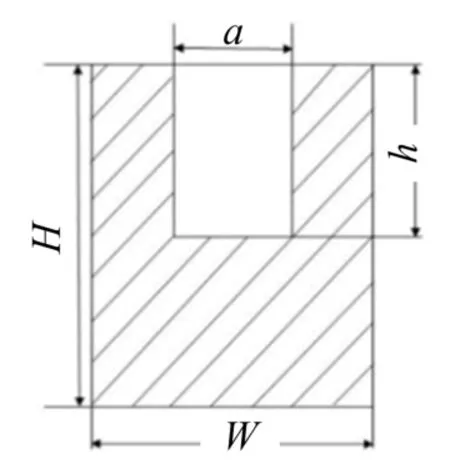
图4 矩形微通道进出口截面示意图

设置12组不同宽高比α=a∕h的值,用于研究α对于微通道流动与换热性能的影响.这12组的几何参数如表2所示.

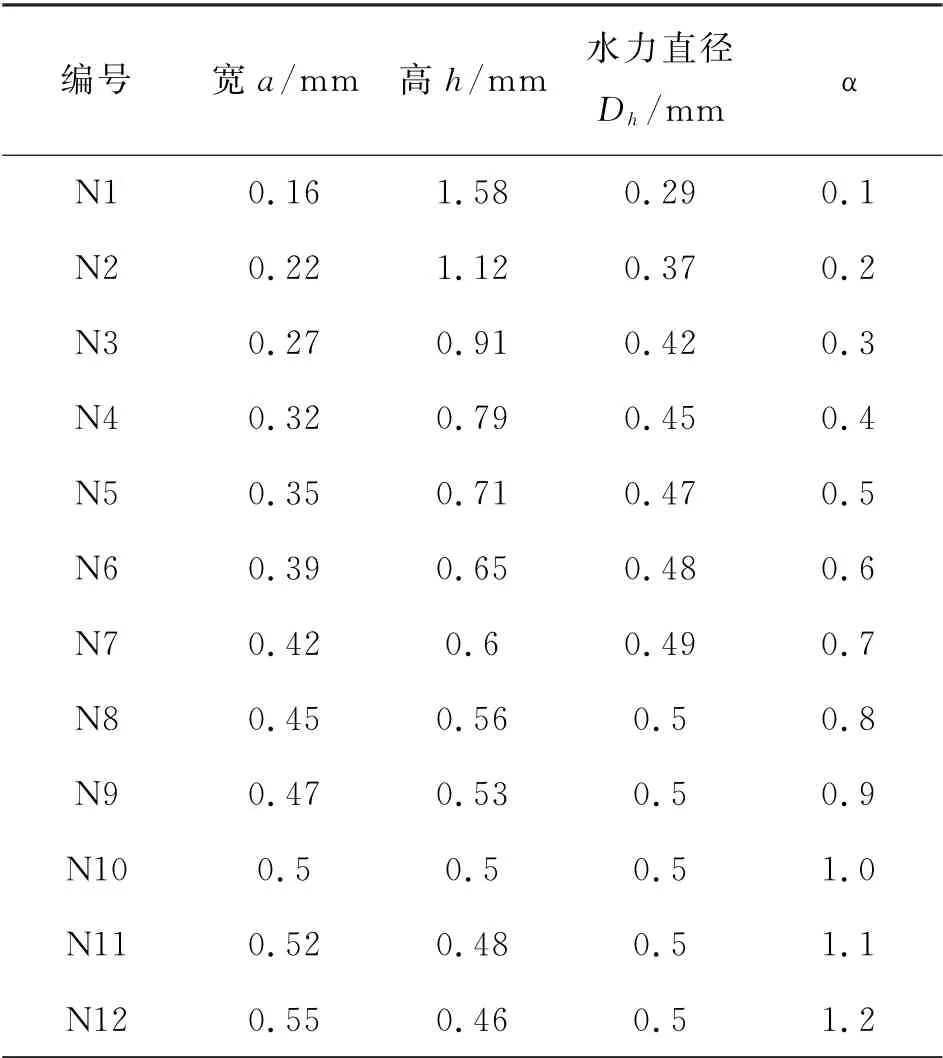
表2 矩形微通道的几何参数

根据图5可以看出微通道的热阻会随着Re数的增大而减小.当200≤Re≤600,热阻随Re数的增大而减小的幅度较大,当Re＞600时,变化趋势趋于平缓,因此要通过减小热阻来提高传热效率,Re数的大小最好处于200～600.当宽高比α≤0.8时,热阻的变化随雷诺数的变化不大,宽高比α＞0.8时,热阻明显增大.在图6中,N1～N12组微通道的压力损失随着Re数的增大而增大.当宽高比α≤0.6时,压力损失ΔP随雷诺数Re的增大变化明显;当宽高比α＞0.6时,压力损失ΔP随雷诺数Re的增大变化不明显.结合图5和图6,本文选择微通道换热器的宽高比为α=0.8.

图5 不同宽高比矩形通道热阻随雷诺数变化规律

图6 不同宽高比矩形通道压损随雷诺数变化规律

3 单个凹槽微通道的流动与传热分析

3.1 Cantor分形数学模型

本文所研究的模型是基于康托尔(Cantor)分形的凹槽模型.其构造过程如下:

(1)在水平方向,将初始表面轮廓长度L0视为闭区间[0,1],第一次分割时将闭区间[0,1]分割为(2s-1)份,其中奇数段与奇数段区间长度相等,偶数段与偶数段区间长度相等,且奇数段区间长度的总和比上总区间长度L0为1/fx(定义fx为沿x方向的分形比,fx＞1).在垂直方向上,偶数段形成凸起,高度设置为h0.

(2)将剩下的奇数段区间继续按照上述方式分割为(2s-1)段,偶数段继续形成凸起,但此时凸起高度为h1,且fx与h0的比值为1/fy(定义fy为沿y方向的分形比,fy＞1).

如图7所示为由s=3的Cantor集合构造的分形曲面,也就是本文的研究模型.

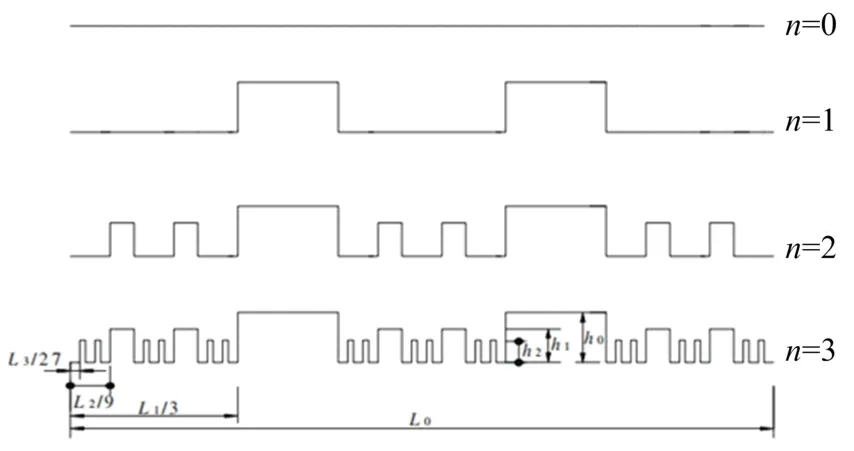
图7 s=3时的康托尔集合

本文选用的模型为s=3时的康托尔分形模型.根据上文,微通道的截面尺寸为:宽a=0.45 mm,高b=0.56 mm.第0级时,初始表面轮廓长度L0=15 mm.取fx=1.25,fy=1.5,h0=0.09 mm.则本文所研究分形微通道模型的尺寸如表3:

表3 分形微通道尺寸

3.2 Cantor分形物理模型

本文微通道的基座尺寸与上述保持一致.固体域材料为铜,流体工质选用去离子水.根据计算值,利用SOLIDWORKS对通道模型N0与分形模型N1、N2、N3进行建模,如图8所示.

图8 微通道的分形凹槽模型

在笛卡尔坐标下,边界条件满足下列方程:

微通道的入口:

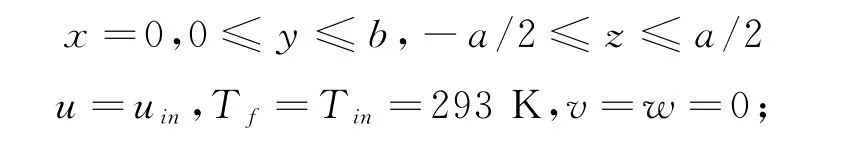
微通道的出口:

3.3 几何结构对微通道流动与传热性能的影响

3.3.1 阵列与分形的影响

为了研究cantor分形微通道的优点,设计了一个与N2具有相同对流换热面积的阵列模型N2*,模型进出口尺寸和通道总长度L0与N0保持一致,即宽a=0.45 mm,高b=0.56 mm,长L0=15 mm.其他尺寸:x方向上,L奇=1mm,L偶=0.75 mm;y方向上,h=0.0675 mm.N2*的模型(部分)如图9所示:

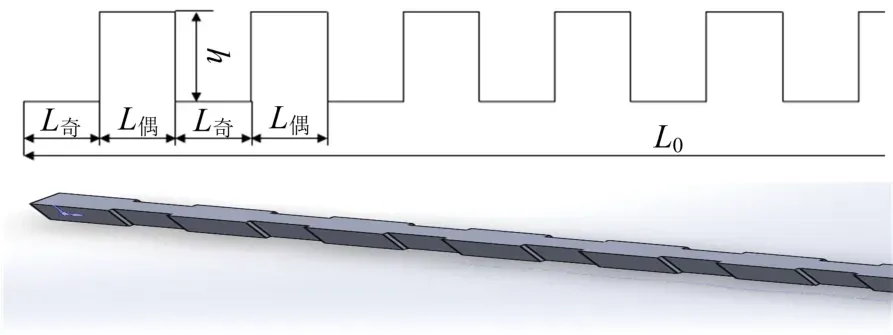
图9 阵列凹槽微通道模型

对模型N0、N1、N2、N3以及N2*进行网格划分后,导入FLUENT软件进行数值计算,初始条件:进口Tin=293 K,进口uin=0.71 m/s,底部热源q=52 W/cm2.

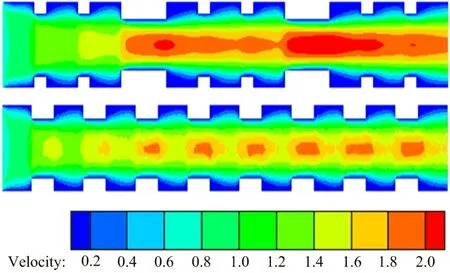
图10 分形模型与阵列模型的管中心面速度云图比较

对比N2和N2*模型,发现阵列模型的中心主流速度在凹槽处虽有明显增加,但是越过凹槽后流体主流流速并不会向后推移;阵列模型的压力分布相较于分形模型进口高压区增多,压力不均匀性增加,其余与分形模型相似.

通过图11不同模型的压降和热阻分析,比较分形模型和阵列模型发现,在增加相同对流换热面积下,热阻相差0.65%,但压降相差了5%.比较N2与N3可以看出热阻仅相差0.57%,但是压降相差了9%.以上可以看出N2能保证热阻降低,具有明显的换热优势.因此采用第二级cantor分形模型.

图11 不同模型压降和热阻的对比

3.3.2 凹槽形状的影响

本文设置了五组不同形状的凹槽结构,包括矩形、三角形、梯形、半椭圆、半正弦结构.其中矩形凹槽微通道的结构尺寸与N2保持一致,其他四种微通道进出口的形状结构尺寸、cantor分形参数、凹槽宽度和深度均与矩形凹槽微通道保持一致,仅形状发生改变.

当进口流速uin=0.71 m/s,底部热流密度q=52 W/cm2时,根据上述五种凹槽模型的数值解可以得到:梯形凹槽结构的加热面平均温度最低,其次是矩形、半正弦、半椭圆、三角形.由模拟结果可以看出,矩形凹槽对中心流体的流速影响最大,其次为梯形、半椭圆、半正弦、三角形.矩形凹槽结构压降最大,其次为梯形、半椭圆、半正弦、三角形,压降的变化趋势与管中心速度的趋势保持一致.

从图12可以看出:从换热角度来说,梯形凹槽微通道的热阻值最小,换热性能表现最优.热阻表现为:梯形＜矩形＜半正弦＜半椭圆＜三角形.从压降角度表现为:三角形＜半正弦＜半椭圆＜梯形＜矩形.根据模拟结果对比这五种结构,矩形的对流换热面积最大,中心流速也是最大的,但是由于凹槽的影响,流体绕过凹槽后,在后方管道近壁面处形成了涡,但此时近壁面处流速不高,形成的涡并不能与主流汇合,反而由于粘性耗散造成了局部能量损失,使压降增大,故矩形凹槽微通道会在凹槽后方形成死穴,换热效果反而不好.梯形、三角形凹槽在一定程度上解决了这一问题,但由于梯形对流换热面积大,中心流体流速高,换热效果好,热阻最低,压降也相对最大.而三角形凹槽对流换热面积少,换热效果不理想,但进出口压降值低,系统消耗能量最少.对于流线型的凹槽,也就是半椭圆和半正弦凹槽来说,对流换热面积的减少、死穴现象的出现、中心主流流速不高等都会造成换热效果的不理想.综合来看采用梯形凹槽微通道的流动换热性能最佳.

图12 不同形状凹槽结构压降和热阻的对比

3.4 几何尺寸对微通道流动与传热性能的影响

本文通过单一变量法对微通道的梯形凹槽尺寸进行优化,寻找最优尺寸,其中包括三个变量:梯形凹槽下表面长度与上表面长度的比值b/a、分形比fx的值(其值与梯形凹槽上表面长度a相关)、分形比fy的值(其值与梯形凹槽的深度h相关).

3.4.1b/a的影响

首先在保持分形比fx和fy不变的情况下(取fx=1.25,fy=1.5,分形级数为2级)改变梯形凹槽下表面长度与上表面长度的比值b/a,设置了11组不同b/a值,取初值b/a=0,此后每组增加0.1,分别为b/a=0、0.1、0.2、0.3、0.4、0.5、0.6、0.7、0.8、0.9、1,建立相应的三维模型,探究b/a的值对微通道流动与传热性能的影响.

由图13可知:随着b/a值的增大,压降逐渐增大.由模拟结果可知,这是由于流体流入凹槽区段后,凹槽下表面宽度的增加,对中心主流区流速的影响明显,由于喷射现象产生的节流效应增强,中心主流区速度剧增,且高速区被拉长.沿流动切面z方向的速度梯度逐渐增大,这使得微通道内部流动阻力增大,压降也增大.而另一方面随着b/a值的增大,流体流过凹槽后形成了涡流,随着涡的发展壮大,粘性耗散增强,也使得压强增大.而热阻的大小则随着b/a值的增大先减小后增大,当凹槽为矩形时又有小幅下降.这说明,由于b/a值的增大,中心主流速度逐渐增大,使得传热效果显著提升,但当b/a≥0.7后,凹槽后方壁面的涡流发展,流体流动死区增大,传热变差.而矩形凹槽的存在,大涡使冷热流体的混合加剧,使得传热有所好转,热阻有所降低.综合对比发现b/a=0.6时微通道的综合性能最优.

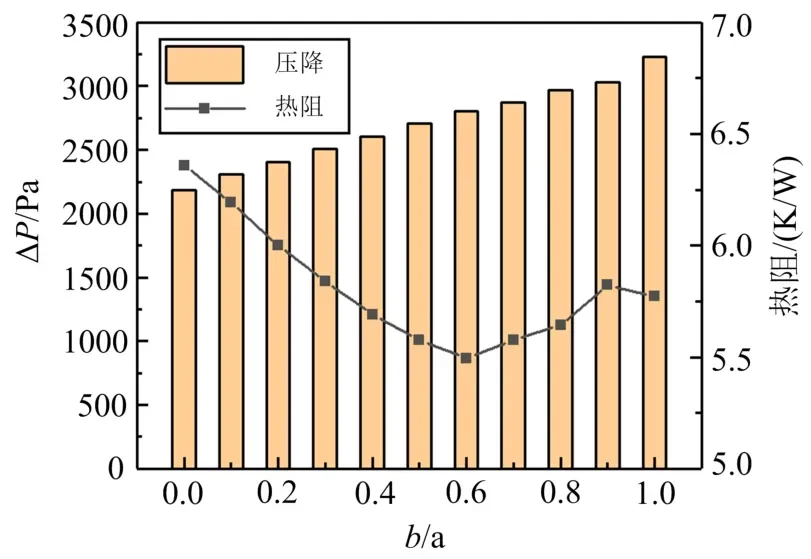
图13 不同b/a值的凹槽的压降和热阻对比

3.4.2fy的影响

为研究分形比fy的影响,在保证b/a=0.6、fx=1.25、其他几何参数不变的条件下,设置了4组不同fy值,取初值fy=1.25,此后每组增加0.25,分别为fy=1.25、fy=1.5、fy=1.75、fy=2.边界条件与前文保持一致.其中fy=1.5组的几何参数与本文中的b/a=0.6组完全一致.

由图14可以看出,随着fy值的增大,压降逐渐减小,热阻逐渐增大.相比于fy=1.25组的压降值3282.42 Pa,其他三组依次降低了7.61%、11.75%、13.92%;相比于fy=1.25组的热阻值5.51 K/W,其他三组依次增加了5.68%、9.75%、14.55%.因此可见fy的大小对进出口压降和对流换热性能都产生一定的影响,且对压降的影响稍大于对热阻影响.这主要是由于fy主要影响小槽的高度,fy值越大,小槽的高度越小,小槽处yoz截面面积越大,喷射节流效应的影响降低,造成流速的降低更加明显,压降随之减小.另一方面小槽的高度降低,流体绕槽后在后方壁面形成的死区减小,粘性耗散减小,对进出口压降的降低有一定的缓解作用,同时也一定程度上有利于对流换热效应.综合对比这四组的换热和流动状况,fy选取1.5时换热性能最优.

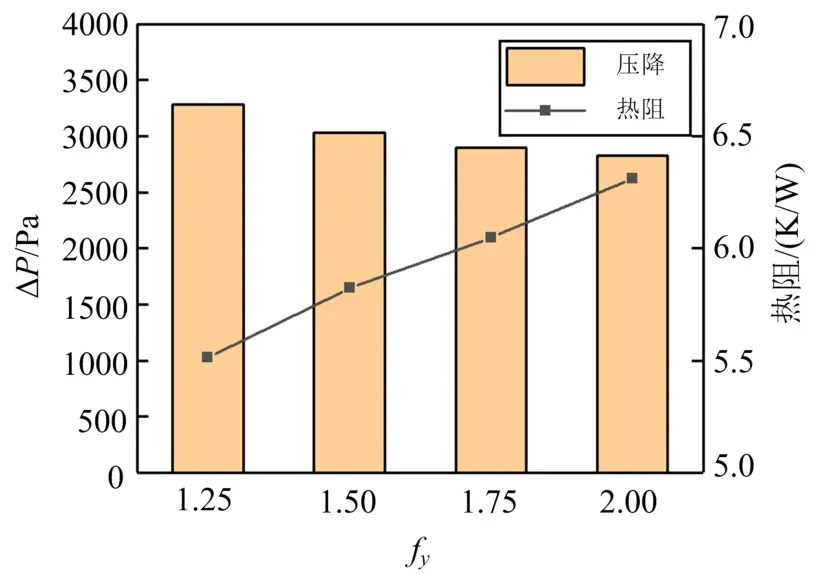
图14 不同fy值的梯形凹槽的压降和热阻对比

3.4.3fx的影响

基于上述研究,本文模型的梯形凹槽取b/a=0.6,fy=1.5,在保持微通道的其他几何尺寸不变的情况下,设置了5组不同fx值,取初值fx=1.25,此后每组增加0.25,分别为fx=1.25、fx=1.5、fx=1.75、fx=2、fx=2.25,fx值的改变主要是对槽的宽度产生了影响,探究fx的改变对微通道的流动与传热特性的影响,以及对综合性能的改变.

其中fx=1.25组与前文中fy=1.5组的几何尺寸完全一致.保证边界条件与初始条件不变.

从图15可以看出:这5种结构中,fx=1.25组的热阻和压降的值均为最小值.说明在此情况下其换热性能最优和外界泵耗最小.相比于fx=1.25组的热阻,其他四组分别依次增加了0.5%、1.3%、1.4%、1.1%;相比于fx=1.25组的压降,其他四组分别依次增加了17%、26.7%、33.4%、38.9%.因此可知fx的大小对换热性能的影响较小,主要是对进出口压降产生影响.随着fx的增大,压降逐渐增大,这是由于随着fx的增大,凹槽尺寸增大,槽与槽之间的距离在减小,流体流过凹槽产生的喷射节流效应加剧,使压降升高;而另一方面流体绕凹槽后形成的涡不能与主流汇合,粘性耗散也会带来一部分的能量损失.故fx=1.25时的换热和流动性能最优.

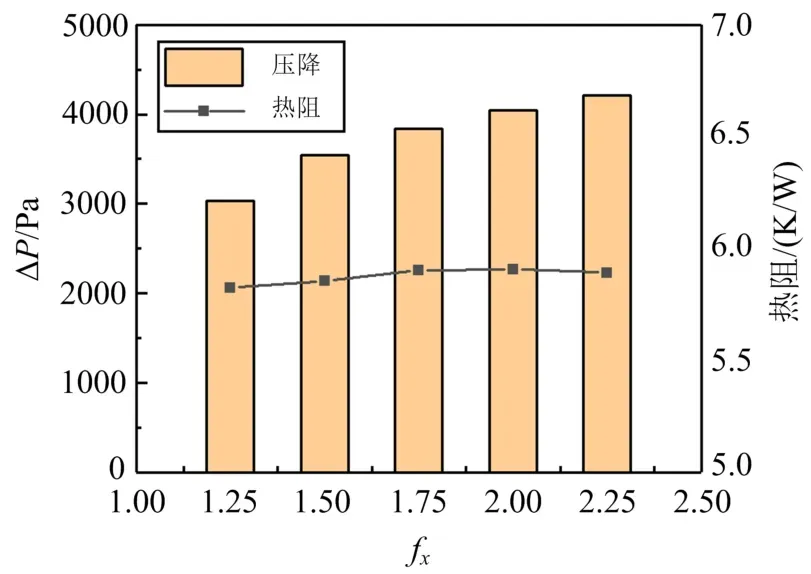
图15 不同fx值的梯形槽的压降和热阻对比

4 结论

为了保证传热效果同时降低流动阻力,本文提出了一种康托尔分型凹槽结构,并针对微通道形状和尺寸、不同康托尔分形级数以及这种康托尔分形结构的凹槽形状,尺寸及不同方向上的分形进行了模拟,得出如下结论:

(1)在相同水力直径和入口雷诺数等运行工况下,对比梯形和三角形微通道,矩形微通道的截面平均努塞尔数Nu最大,换热效果最好.对于进出口截面面积一定的矩形微通道,宽高比α越大,水力直径越大,压力损失较小,但此时微通道的热阻越大,因此较大的传热效率往往带来较大的压力损失.研究发现,宽高比α介于0.6至0.8之间时具有较好的综合性能.

(2)阵列凹槽微通道和康托尔分型凹槽微通道都能有效提升微通道的换热效率.但是阵列模型的中心主流速度在凹槽处虽有增加,越过凹槽后流体主流流速并不会向后推移;阵列模型的压力分布相较于分形模型进口高压区增多,压力不均匀性也增加.综合对比发现,第二级康托尔分形模型N2既能保证热阻显著降低,又能相比阵列结构降低压降,具有明显的换热优势.

(3)梯形凹槽下表面长度与上表面长度的比值b/a、分形比fx、分形比fy这些几何尺寸对凹槽微通道的流动与传热有较大影响.当b/a=0.6时,主流中心流速较大,绕过凹槽后壁面形成的死区还不明显,对传热的恶化暂时可忽略不计;当fx=1.25时,相比其他四组,热阻最多降低了1.4%,压降最多降低了38.9%,故fx=1.25时的换热和流动性能最优;当fy=1.5时,相比其他三组,热阻最多降低了14.55%,压降最多降低了13.92%,故fy=1.5时的换热和流动性能最优.