4～20 K温区固体界面导热填料接触热阻实验研究*

刘少帅潘小珊陈志超丁磊蒋珍华吴亦农

1.中国科学院上海技术物理研究所,上海,200083 2.中国科学院大学,北京,100049

1 引言

随着深空探索、量子科学、大科学技术等工程应用的发展[1-4],4～20 K温区作为液氦和液氢的关键温区,在机理研究和工程技术中均体现重要价值.低温技术和传热密切相关,温度越低,温差引起的代价越大,特别是4 K温区0.1 K的温差往往会引起几十瓦功耗的增加,从而导致制冷机性能降低.深低温研究应用中的关键之一是降低界面之间的传热温差[5-7].

深低温区固体与固体接触界面的传热问题,由于材料属性变化等因素,极易引起工程应用或仿真设计时量化设计偏差.从宏观的角度,由于金属表面的不完全接触,当金属接触界面通过热流时导热流线向接触点收缩导致接触界面产生明显的温度跳跃.特别是金属材料处于液氦温区时,极低温温度会使接触面发生形变并增大了金属材料的硬度,减小了实际接触面积从而导致界面接触热阻增大[8].从微观角度,金属的热传导主要由自由电子的迁移传递能量.电子在两界面间热传输过程中与材料缺陷处碰撞和散射、受边界散射、热载子之间的碰撞和散射从而导致接触热阻的产生[9].界面导热材料TIM(Thermal Interface Materials)在电子封装和航天航空热管理中扮演着重要的角色,通过在固体接触界面处填充性能良好的TIM可以改善芯片和探测器的散热[10].

瞬态法是国内外固体界面接触热阻的实验研究中最常用的实验测试方法,大多和美国测试标准设备ASTM D5470-06测试原理相似[11].由于对样品轴向做了多种绝热措施和抽真空处理,可以认为施加的全部热流都沿轴向传递,即使在靠近接触界面处由于变形存在三维的热传递,离开接触面后继续沿轴向传递.从宏观上看,热量在样品间的传递方向可认为仅沿轴向传递[12].当流经两表面的热流量为Q,温差为ΔTc时,接触热阻定义为两表面温差和热流量之比[13].徐烈等人对液氮温区固体界面接触热阻进行实验研究时,将整个实验装置放于液氮热沉中,并设置防辐射冷屏,加载方式采用波纹管,一方面波纹管可以弹性伸缩另一方面也保证了真空腔的密封性[14].饶荣水等基于GM制冷机,搭建实验装置研究了20～180 K界面接触热阻,在装置中为了提高实验准确度,在实验装置外放置了低温防辐射冷屏,加热器的上方用绝热材料将样品和环境进行热隔离并通过温度控制器控制热沉的温度[15].Kumar等人基于稳态实验法,在50～300 K温区对铝、镁和不锈钢材料界面接触热阻进行实验研究,得到了界面接触热阻与界面粗糙度、界面压力之间的关系[16].

目前国际上接触热阻的测试大多集中在20 K及以上温区,主要是由于在对接触热阻特别是深低温温区固体界面接触热阻进行测量时,对测试装置防漏热措施和温控的要求更高,所以测量低温接触热阻比测量常温接触热阻的实验装置更为复杂[17].对比于常温及液氮温区的接触热阻实验,4～20 K温区固体界面接触热阻实验存在以下难点:(1)4～20 K温度较低,与常温300 K存在量级差别,在对4～20 K温区固体界面接触热阻测试时对热沉温度的稳定性需求较大,精准测量一般要求m K量级稳定性,对低温冷源测试要求较高.(2)4～20 K温区接触热阻实验对实验装置漏热防护措施要求较高,在百m W加热量下的漏热要求小于1 m W的量级.(3)涉及深低温的制冷机降温/回温较长,且稳定时间慢,对温度、压力的测量精度要求高.

针对4～20 K温区接触热阻测试问题,本文设计了一个压力、低温温度可调的实验方案,对低温工程应用中常用的高纯无氧铜和不锈钢材料界面热阻进行试验测量,获得不同压力、温度下的接触热阻变化关系,并进一步拟合关联式,为定量应用奠定基础.

2 低温固体界面填充介质热阻特性

在真空环境中两接触界面无填充导热材料时由于没有空气传递热量,不完全接触部位主要靠辐射传热,从而导致接触热阻过大进而增大温差影响实际工程应用,填充合适的界面导热材料是降低界面接触热阻的主要方式.热流通过固体-TIM-固体结构产生的接触热阻示意图如图1所示.铟和Apiezon N导热硅脂具有高导热、良好的延展性,被广泛应用于工程技术中作为低温固体界面填充物质,其导热系数如图2所示.在两接触面间添加界面导热材料时,样品界面间的总接触热阻等于上样品与界面导热材料的接触热阻RTCR1、界面导热材料的导热热阻RBLT和下样品与界面导热材料的接触热阻RTCR2的和:

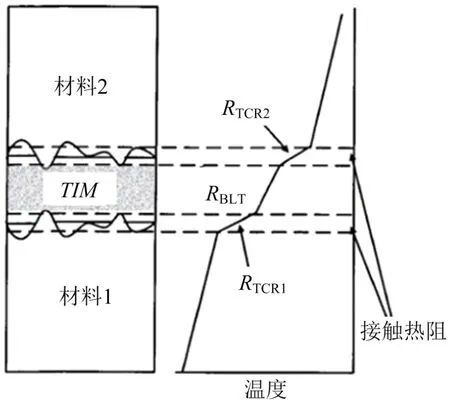
图1 热流通过固体-TIM-固体结构产生的接触热阻示意图[18]

图2 铟金属和Apiezon N导热硅脂导热系数随温度变化曲线图[19]

3 深低温接触热阻测试实验台

3.1 实验装置设计

在设计搭建测试实验台时要考虑温度、压力等变工况测试的要求,尽可能地减少测试操作时间以及在测量误差尽可能小的情况下准确测量出不同温度、压力下,两接触表面温度、热流量,以准确推算出接触热阻数值.所设计的4～20 K固体界面接触热阻实验系统示意图及实物图分别如图3和图4所示,包括测试系统、真空泵组、GM制冷机系统和数据采集系统.本低温固体界面接触热阻实验台采用中船重工鹏力超低温技术有限公司生产的两级GM制冷机作为冷源,可以满足4～20 K变温区调节需求.GM两级冷头上分别布置冷屏并包裹绝热多层材料,在样品和承压波纹管之间间隔绝热材料,并对进入波纹管的气体尽可能预冷以减少波纹管和样品之间的温差,从而减少样品导热漏热量.在波纹管管路外设置压力传感器以测量波纹管内的压强.在上下夹具,样品表面和聚酰亚胺表面都设置温度传感器以测量各个部件的温度,加热数据和温度数据由中科院上海技术物理研究所自主Lab VIEW编程的数据采集程序进行采集和存储.

图3 4～20 K固体界面接触热阻实验系统示意图

图4 实验测试部分实物图

该实验装置具有以下特点:(1)可以同时搭载两个接触热阻测试实验台,有效地减少了开机关机回常温等操作时间;(2)利用主被动控制方法,对GM二级冷头温度进行调节的同时极大地降低了GM冷头温度波动,提高了测量结果的准确度;(3)利用预冷后的气体冲压承压波纹管,改变低温工况下施加在样品上的压力;(4)设置防辐射冷屏、绝热多层材料和高真空环境,使得样品表面辐射漏热减小的同时温度传感器表面辐射减小,提高了测温的准确性.

3.2 低温波纹管压力调节施加校核

在利用承压波纹管进行压力调节时,气体压强升高导致波纹管产生形变,由于波纹管上端面被限制只能向下发生形变,从而对样品产生向下压力,需要明确气体充气压力和两样品表面所承受的界面压力之间的关系.实验中采用精密感压纸对样品之间的界面压力进行测量.LLW型号感压纸由A和C胶片组成,A纸是涂有红色微粒材料的胶片,C纸是涂有显影材料的胶片.当两片胶片受到力挤压时互相作用,C纸发生不同程度的变色,根据接触面和接触压力的不同显色范围和深浅程度不同,以此通过与扫描仪录入的比色卡比对可以得出界面压力值.

本文压力对接触热阻的影响研究主要在0～3 MPa范围内.改变波纹管的充气量测量多组数据,得到了不同充气压力下的感压显色C纸(见图5),并拟合样品界面平均压力随波纹管充气压力关系曲线关系式(式2).样品接触界面所受压力随波纹管充气压力变化趋势图如图6所示.

图5 不同充气压力下的感压显色C纸

图6 样品接触界面所受平均压力随波纹管充气压力变化趋势图

在实验过程中通过自主编程的Lab VIEW程序实时监测压力传感器的数值,并据样品所受到的平均界面压力和波纹管充气压力关系式得出样品接触界面所受压力值.

式中,x为充气压力,MPa;y为样品接触界面压力,MPa.

3.3 温度重复性验证测试

为了检验接触热阻测试实验的重复性和可靠性,当表面粗糙度Ra=0.80μm,接触界面受到的压力P=0.67 MPa,加热量Q=13.1 m W对无氧铜-无氧铜样品接触热阻值进行3次重复实验.3次重复性测量均进行重新回温、拆装样品、重新加压和降温处理.同一界面压力下4～20 K温区接触热阻3次重复测试结果如图7所示.从图中可以看出,3次实验结果基本一致,测试误差小于±5%.

图7 无氧铜样品对接触热阻值随温度变化3次测量值

3.4 测试误差

由式(3)可知界面接触热阻测量误差与两界面温差ΔTc测量误差、面积A测量误差和加热量Q测量误差有关.本实验测试过程中各误差如表1所示.

表1 实验测试过程中各参数测试误差

由误差传递公式可得接触热阻的测量误差:

3.5 实验样品

本文接触热阻测试实验样品为深低温技术常用的高纯无氧铜和不锈钢材料,样品由样品夹具固定在测试平台上.本实验所用的无氧铜和不锈钢样品规格相同,形状为圆柱形,直径约20 mm,高度约30 mm,实验样品实物图及接触表面形貌如图8所示.如图所示在接触界面周围均布四个长8 mm、宽3 mm、厚度约1 mm测温翅片,以测量接触界面的温度.

图8 实验样品及接触界面表面形貌图(粗糙度0.8μm)

4 实验结果分析及半经验公式拟合

4.1 不同温度下两种界面导热材料的接触热阻变化对比

图9至图10分别为无氧铜-无氧铜样品、不锈钢-不锈钢样品在不同界面导热材料(Apiezon N导热硅脂和铟片)下,接触热阻值随着界面平均温度变化的趋势图,基本工况:Ra=1.88μm,P=0.67 MPa.无论是填充铟片还是Apiezon N导热硅脂,两接触界面间接触热阻随着温度的升高而减小和无界面导热材料时的趋势一致.相同条件下,相比于无界面导热材料,添加界面导热材料后无氧铜-无氧铜、不锈钢-不锈钢样品之间的接触热阻明显变小.主要是因为真空环境中,两样品界面间间隙由于没有气体介质可以进行导热换热,辐射为主要换热方式.增加界面导热材料后,由于界面导热材料良好的延展性和外力载荷的加载,铟片和Apiezon N导热硅脂填充到两接触面之间的空隙,使得辐射换热变成了界面导热材料的导热换热,换热效果变好,所以接触热阻也相应的减小.无界面导热材料状态时,未接触部位主要通过辐射换热来传递能量,根据玻尔兹曼定律可知Q∝T4,温度越大辐射换热越强,所以接触热阻减小幅度较大.从图9(a)和10(a)可以看出,在4～20 K的温度区间内与温度影响相比较,增加界面导热材料对界面接触热阻的影响更为显著.当添加界面导热材料后,接触热阻还和界面导热材料的导热热阻有关.从图9(b)和10(b)可知,添加铟片后的接触热阻值随温度的变化较Apiezon N导热硅脂小,这是因为在4～20 K温区Apiezon N导热硅脂、铟片的导热系数随着温度变化为线性变化,且铟片的导热系数随着温度的升高有所下降,减弱了一部分热量传递,所以铟片接触热阻随温度变化最小.

图9 无氧铜-无氧铜样品接触热阻随界面平均温度变化的趋势图

图10 不锈钢-不锈钢样品接触热阻随界面平均温度变化的趋势图

4.2 不同压力下两种界面导热材料的接触热阻变化对比

图11 为无氧铜-无氧铜样品接触热阻值随着界面平均压力变化的趋势图,基本工况:下样品温度4.5 K.随着界面压力的增加,添加界面导热材料后无氧铜-无氧铜样品界面接触热阻逐渐减小.一方面,接触界面压力的增大导致无氧铜接触界面层产生位移,使得晶格缺陷得以填补,提升了无氧铜和界面导热材料之间的接触界面中电子热传递的性能,传热效果变好,因而上样品与界面导热材料的接触热阻RTCR1和下样品与界面导热材料的接触热阻RTCR2之和减小,总的接触热阻值减小.另一方面,由于导热材料良好的延展性,当压力增大时界面未接触部位得到更充分填充,增加接触面积,降低RTCR1和RTCR2.界面压力的增加挤出多余的界面导热材料,使得界面导热材料的导热热阻RBLT减小,因此总的界面接触热阻随着界面压力的增加而减小.加热量为10.5m W左右,无氧铜-无氧铜样品界面平均温度为20 K时,界面平均压力从0.67 MPa增加到2.8 MPa,压力增加了3.18倍,界面导热材料为Apiezon N导热硅脂接触热阻值从2.27×10-3m2·K/W减小到1.83×10-3m2·K/W,界面导热材料为铟片接触热阻2.17×10-3m2·K/W减小到1.33×10-3m2·K/W.由于低温下两固体接触界面收缩,增大了两接触界面间的间隙.铟片在低温下延展性良好,当压力增大时能很好地填充到两接触界面空隙中.而Apiezon N导热硅脂在常温下填充时为液状,当温度为深低温即4.5 K时由于其物理特性逐渐凝固成固态,延展性较差,无法很好地填充.因此在增加加载压力的情况下,铟片能够更好地填充到两样品未接触部分的空隙中,增强界面间的传热效果,接触热阻减小幅度也更大.

图11 无氧铜-无氧铜样品接触热阻随界面平均压力变化的趋势图

4.3 表面粗糙度对接触热阻的影响实验

固体材料表面形貌差异导致接触界面的粗糙度的不同,表面粗糙度通过影响实际接触面积,从而影响接触热阻的值.无氧铜-无氧铜样品、不锈钢-不锈钢样品接触热阻随界面平均粗糙度变化趋势图如图12所示.随着界面平均粗糙度的增加,无氧铜-无氧铜样品和不锈钢-不锈钢样品界面接触热阻呈增加的趋势,这是由于粗糙度的增加导致接触界面间隙变大,热流经过接触界面时收缩剧烈传热效果变差,两界面温差变大进而导致界面接触热阻变大.另一方面,粗糙度的增加使得实际接触凸点数较粗糙度小的界面的实际接触凸点少,实际接触面积减小,也会导致接触热阻的增大.温度越低,无氧铜和不锈钢界面接触热阻受粗糙度的影响越大.

图12 不同样品接触热阻随界面平均粗糙度变化趋势图

如图13所示,当界面温度为12 K,界面压力为0.67MPa时,粗糙度 从0.67μm增加1.8倍 到1.88μm,不锈钢界面接触热阻从79.43×10-3m2·K/W增大到141.33×10-3m2·K/W,无氧铜界面接触热阻从12.03×10-3m2·K/W增大到54.45×10-3m2·K/W.当实验条件一样时,无氧铜界面接触热阻受表面粗糙度的影响较大,因为当粗糙度增大时,实际凸点数减小,无氧铜导热系数较大,界面间总传递的热流量幅度较大,所以接触热阻增大幅度较不锈钢也较大.

图13 不锈钢-不锈钢和无氧铜-无氧铜样品接触热阻随粗糙度变化的趋势图

4.4 半经验计算模型

建立合适的接触热阻半经验公式,有利于帮助指导工程应用和仿真计算.本研究中利用此实验结构,开展了不同粗糙度、温度、压力工况下的热阻测试实验,基本规律与上述部分的结果一致,不再赘述,并基于实验结果进行关联式拟合.金属表面接触热阻一般与表面粗糙度、材料硬度/强度/弹性模量呈正相关,与材料导热系数、温度、接触面压力呈负相关即:

其中,σ为粗糙度均方根值,m;λ平均热导率,W/(m·K);P为接触面所受压力,N/m2;E为杨氏弹性模量,N/m2;T为接触表面温度,K;

因此,可以将两金属接触表面接触热阻表达成导热系数、表面粗糙度、接触压力、材料硬度/强度/弹性模量的函数:

式中,C1、C2、C3、C4、C5、C6为常数,为了简化计算,可以改写为对数形式:

本文采用最小二乘法求解系数:C1=1.842910-7,C2=1.7388,C3=-0.1720,C4=-4.4834,C5=0.0395,C6=5.0914.得出4～20 K无氧铜-无氧铜界面接触热阻值关于表面粗糙度、材料弹性模量、材料导热系数、温度、接触面压力的半经验公式为:

式中,RTCR为界面接触热阻,10-3m2·K/W;σ为表面粗糙度,μm;λ(T)为材料导热系数,W/(m·K);E(T)为材料杨氏模量,GPa;P为界面压力,MPa;T为界面温度,K.当工况一致时无氧铜-无氧铜样品界面接触热阻随温度、压力的增大而减小,随表面粗糙度的增大而增大.将半经验公式计算得出的无氧铜-无氧铜样品界面接触热阻与实验数据相比较,如图14所示.从图形可以看出,用最小二乘法建立的半经验公式和实验数据的变化趋势一致且数值较吻合,半经验公式较为可靠.

图14 无氧铜-无氧铜样品界面接触热阻半经验公式计算值和实验测量值相比较

根据无氧铜-无氧铜样品界面接触热阻4～20 K半经验公式,得到接触热阻随界面平均温度、粗糙度的变化曲线图和接触热阻随界面平均温度、压力的变化曲线图如图15和图16所示.根据图15可知,界面温度和表面粗糙度对接触热阻的影响都很显著;随着温度的增加和表面粗糙度的减小,界面接触热阻呈减小的趋势;界面粗糙度越大,无氧铜-无氧铜样品界面接触热阻受界面平均温度的影响越大;温度越低,无氧铜-无氧铜样品界面接触热阻受表面粗糙度的影响越大.如图16所示,随着界面压力的增加,无氧铜-无氧铜样品界面接触热阻呈减小的趋势,但是与界面平均温度相比,界面平均压力对其影响不显著.

图15 无氧铜-无氧铜样品界面接触热阻随界面平均温度和粗糙度变化的曲线图

图16 无氧铜-无氧铜样品界面接触热阻随界面平均温度和压力变化的曲线图

5 结论

通过搭建4～20 K变温区变压力工况接触热阻试验测试台,分别测试固体界面填充金属铟和低温导热硅脂时的接触热阻,得到如下结论:(1)无论是否添加界面导热材料及添加何种界面导热材料,4～20 K低温下固体接触热阻均随着温度升高而减小;(2)相同界面温度、界面压力和表面粗糙度的情况下,填充导热系数小的Apiezon N导热硅脂界面导热材料的接触热阻值,大于导热系数大的铟片界面导热材料接触热阻值;(3)随着界面压力的增加,界面接触热阻逐渐减小,增加相同的界面压力,添加铟片的无氧铜样品接触热阻减小幅度更大.基于本研究中实验台测试的数据所拟合的关联式,可以得到4～20 K接触热阻与平均温度/压力之间的变化关系.该研究为我国量子科学和空间探测的深低温技术工程应用提供参考.