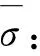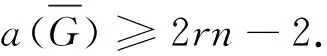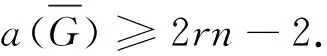两类n-部图及其补图的无圈染色
彭 悦,田双亮
(西北民族大学 数学与计算机科学学院,甘肃 兰州 730030)
0 引言
本文所考虑的图G都是有限无向的简单连通图,用V(G)与E(G)分别表示G的顶点集和边集,用Δ(G)表示G的最大度,并记(x)k=xmodk,其中x为整数,k为正整数,用rH表示r个同构于图H的图的不交并,其中r≥2.

无圈染色概念是Grünbaum于1973年在文献[1]中用代入法求解稀疏对称Hessian矩阵的高速计算背景下产生的.Fertin等人在文献[2]中给出了d-维网格的无圈色数的上界为d+1;无圈染色是NP问题,其在特殊图类上的复杂性的大多数结果都是否定的.特别地,即使仅限于二部图[3-4],这个问题仍是NP问题.文献[5]证明了三连通图的无圈色数为4,除非它是K4或者K3,3,否则K4和K3,3的无圈色数是5.根据无圈染色定义,显然有以下两个引理:
引理1若G的连通分支为G1,G2,…,Gω,则a(G)=max{a(Gi)|1≤i≤ω}.
本文主要研究完全n-部图Kr1,r2,…,rn与二部图rC2n及其补图的无圈染色.文中未说明的符号和术语见文献[6].
1 主要结果及其证明
关于完全n-部图及其补图的无圈染色有以下结果:
定理1对于任意正整数r1,r2,…,rn,有
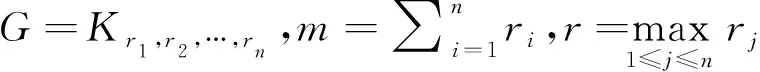

先证明a(G)≥m-r+1.假设a(G)≤m-r,且σ是G的一个(m-r)-无圈染色.为叙述方便,用C(S)表示顶点子集S中顶点在σ下的颜色构成的集合,下文含义相同,不再赘述.显然,有
1≤|C(Vi)|≤ri,i=1,2,…,n;
C(Vi)∩C(Vj)=φ,i,j=1,2,…,n,i≠j;
易证,存在惟一i0∈{1,2,…,n},使得|C(Vi0)| 这与σ的定义矛盾.假设存在i0,i1∈{1,2,…,n},使得i0≠i1,且 |C(Vi0)| 由定理1可直接得到以下推论: 关于二部图rC2n及其补图的无圈染色,有以下结果: 显然,G是具有二分类(X,Y)的二部图. |C(Y)|=rn.又因σ所用颜色数为2rn-3,所以C(X)∩C(Y)=.另外,可以证明以下结论: 1) 存在i0∈{1,2,…,r},使得C(Xi0)∩C(Yi0)≠. 2) 若存在i0∈{1,2,…,r},使得C(Xi0)∩C(Yi0)≠,则对任意j∈{1,2,…,r}-{i0},有C(Xj)∩C(Yj)=. 3)C(X)∩C(Y)≤2. 事实上,假设结论1)不成立,即对任意j∈{1,2,…,r},使得C(Xj)∩C(Yj)=.取a∈C(X)∩C(Y),则存在不同整数i0,j0∈{1,2,…,r},使得a∈C(Xi0),a∈C(Yi0),于是存在x∈Xi0,y∈Yi0,使得σ(x)=σ(y)=a.注意到,Xio中顶点与Yio中顶点在中都是相邻的,所以x与y在中相邻,这就产生相邻顶点染相同颜色的情况,与σ的定义矛盾.因此,结论1)成立. 假设结论2)不成立,即存在j0∈{1,2,…,r}-{i0},使得C(Xj0)∩C(Yj0)≠.取a∈C(Xi0)∩C(Yi0),b∈C(Xj0)∩C(Yj0)以及x∈Xi0,y∈Yi0,x'∈Xj0,y'∈Yj0使得σ(x)=σ(y)=a,σ(x')=σ(y')=b,显然a≠b.在中,因Xi0中顶点与Yj0中顶点都是相邻的,Xj0中顶点与Yi0中顶点都是相邻的,所以x与y'相邻,y与x'相邻.而x与x',y与y'在中相邻,于是形成了4阶2色圈:C4=xy'yx'x,这与σ定义矛盾.因此,结论2)成立.