复合材料机翼热气弹剪裁研究及分析系统研发

薛 程 李彦斌 杭晓晨 郑 浩 王天怡 费庆国

(1东南大学机械工程学院, 南京 211189)(2东南大学江苏省空天机械装备工程研究中心, 南京 211189)(3南京林业大学机械电子工程学院, 南京 210037)

高超声速飞行器具备超高速巡航、快速突防、机动性强等战略优势,能实现远距离快速响应和精准打击,其未来战略地位显著[1-2].而飞行器在服役过程中载荷环境恶劣,气动效应复杂[3-5];其中,气动热引起的以机翼热颤振为代表的气弹效应是影响飞行器安全飞行的关键因素.为得到复杂热载荷环境下最优的气动弹性效果,研究者们通常开展机翼的结构优化设计研究.

复合材料具有比强度高、比刚度大、抗振抗疲劳、可设计自由度高等特点[6-7],在航空航天结构设计领域受到研究者的广泛关注.先进复合材料制造工艺的成熟使得复合材料气弹剪裁设计成为可能[8-9].复材层合板机翼的气弹剪裁主要是通过改变基体材料、纤维布局、铺层角度、铺层厚度等方式调整结构的基本耦合刚度,以期达到最佳的气弹特性效果.唐文艳等[10]采用整数编码和延长父代个体寿命的方式对遗传算法进行改进,提高种群多样性的同时保证了改进算法的有效性,拓展了遗传算法在复材层合板铺层优化设计中的应用.金达锋等[11]针对应力变化复杂的CFRP层合板,通过划分结构子铺层并基于遗传算法优化子铺层的位置、尺寸、铺层数和铺层顺序,得到满足复杂强度要求且质量最优的结构设计方案.Almeida等[12]以结构质量、等载荷下结构的非线性变形量和计算效率为目标函数,结合非线性有限元分析和遗传算法对典型复合材料层合板进行多目标优化.Tanaka等[13]以Christensen失效准则和平均曲率为目标函数对CFRP层合板进行铺层优化,以此获得了高强度且质量最优的变厚度层合板设计方案.

目前,国内外针对复合材料层合板机翼结构的气弹剪裁优化的研究已有坚实的理论基础,但用于高超声速且考虑颤振约束的热气弹剪裁研究较少,国内也缺乏可供使用的集成化工业软件.本文针对典型飞行工况下高超声速飞行器气弹优化问题,基于C/C++开源环境开发Aero-Opt自主工业化集成软件.该分析系统功能全面,可移植性强,对于高超声速飞行器前期优化设计的工程问题具有重要指导意义.

1 高超声速气动热环境载荷模拟

高超声速飞行器随着飞行马赫数的提升,其真实服役环境愈加恶劣.为获取在复杂载荷环境下飞行器的最优气弹特性,对飞行器气动热的有效模拟和结构气动弹性边界的准确预测至关重要[14].本节以一典型复合材料机翼模型开展高超声速飞行工况下的气动加热效应研究,结构有限元模型如图1所示.

图1 典型复合材料机翼有限元模型

上述模型中的翼肋、腹板、梁缘均采用TA7材料,蒙皮采用648环氧树脂;其余结构的尺寸参数如表1所示.

表1 结构尺寸参数

在进行三维模型仿真时,控制方程选用三维可压缩Navier-Stokes方程.选用来流气体的参考温度、参考压强、参考密度、参考时间长、参考黏性参数、参考长度对方程进行无量纲处理,则有

(1)

为求得机翼外表面气动热分布,对外流场进行建模及边界设定,采用压力远场边界条件和无滑移边界条件,压力出口根据零梯度外推;整体模型采用结构化网格进行划分,为提高仿真结果精度,壁面与外流场接触边界网格做加密处理.网格划分结果如图2和图3所示.

图2 流场模型整体示意图

图3 接触面网格划分图

红色区域表示外流场模型,绿色区域表示机翼与流场的接触面,蓝色区域表示机翼固支端处外流场边界.针对典型的高超声速飞行工况(飞行高度20 km,马赫数5～8),设置来流温度为234.552 K,压强设为5 466 Pa,壁面温度设为273.15 K,采用Spalart-Allmaras湍流模型,对该机翼模型进行流固热有限元仿真分析.气动加热效应引起的热流密度分布结果如图4所示.由图可见,机翼冷壁热流密度在前缘处达到最大,并向后缘方向逐步递减.

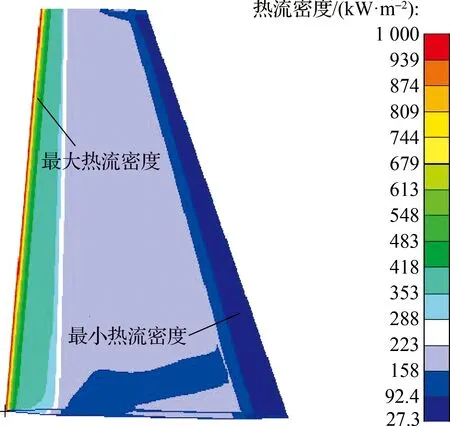
(a) 马赫数5

(b) 马赫数6

(c) 马赫数7

(d) 马赫数8

高速飞行器服役状态下,驻点处的热流密度最能直观地反映机翼的气动加热情况.在机翼工程设计阶段,常用Kemp等[15]提出的经验公式(简称K-R公式)来计算驻点热流密度值.K-R公式定义如下：

(2)

式中,qws为待求解的驻点处热流密度,W/m2;ρ∞为来流密度,kg/m3;v∞为飞行速度,m/s;RN为驻点处曲率半径,m;hs和hw分别为滞止焓值和壁温下的气体焓值,J/kg;ρ0为标准状态下的空气密度,1.225 kg/m3;vc为第一宇宙速度,7 900 m/s.

基于Rose-Stark的激波试验数据,研究者又对上述K-R公式进行了修正[16],进一步提高了该公式与试验数据的拟合度.修正后公式如下:

(3)

式中,h300K为300 K温度下气体的焓值,J/kg.

为验证有限元仿真的正确性,将上述工况仿真得到的驻点热流密度值与K-R公式和修正K-R公式计算得到的驻点热流密度值进行对比,结果如表2所示.可以看出,仿真结果与修正前后K-R公式计算得到的值基本吻合,且误差随着飞行马赫数的提升呈减小的趋势,验证了仿真结果的可靠性.

表2 不同计算方法下驻点热流密度 kW/m2

考虑到壁面温升与热流密度变化之间存在耦合关系,需将计算得到的冷壁热流转化为热壁热流.热壁热流和冷壁热流之间的转换关系式可写为

(4)

式中,qh和qc分别为热壁热流密度和冷壁热流密度,W/m2;hr为恢复温度下的气体焓值,J/kg;ε为表面辐射系数;σ为玻尔兹曼常数,1.38×10-23J/K;T为表面壁温,K.

由于整个转化过程需在瞬态过程下完成,因此需对每个时刻的热流密度进行不断迭代,以求得最终的热壁热流密度.转换结果如图5所示.

(a) 马赫数5

(b) 马赫数6

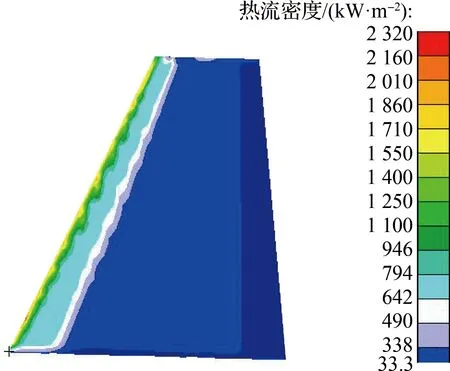
(c) 马赫数7

(d) 马赫数8

2 热颤振响应分析及优化

2.1 热模态分析

将上一阶段仿真得到的热流密度作为载荷加载到结构中,以求解机翼温度梯度场.之后,以300 K常温下机翼的结构振动特性为参照对象,求解机翼在高温下结构的一阶弯曲和一阶扭转模态,如图6所示.通过比较高温和常温下的一阶弯曲和扭转模态可知,气动热效应使得结构一阶弯扭固有频率均有不同程度的降低,而振型幅值增大,这主要是因为气动热效应使得结构总体刚度软化,但该影响并未导致模态跳阶现象发生.

2.2 热颤振求解

机翼在高温热载荷作用下,结构刚度和部分材料参数发生变化;同时,温度梯度带来了额外热应力,使得结构产生附加刚度矩阵.高超声速飞行环境导致的气动热效应对颤振边界的影响不可忽略,本研究基于机翼弯扭模态颤振机理并耦合高超气动热,对结构进行热颤振分析.在拉氏域中,对于此类经典颤振问题,其热颤振方程可写为

(5)

式中,M为广义质量矩阵;Kσ和KT分别为弹性刚度矩阵和热刚度矩阵;Q为广义气动力矩阵;q为广义模态坐标;s为复变量;L为参考长度,m;V为未扰动流的速度,m/s;q∞为动压,Pa.

系统热颤振方程采用g法来求解.针对马赫数为8的工况,比较不同的飞行高度下结构在常温和高温时的阻尼特性,如图7所示.通过阻尼曲线由负到正穿越0阻尼的交越点可以判断系统的颤振边界.从图中可以得出,当飞行高度大于20 km时,颤振边界随着高度的增加而提高;处于同一飞行高度时,高温下的颤振边界相较于常温时出现得更早.

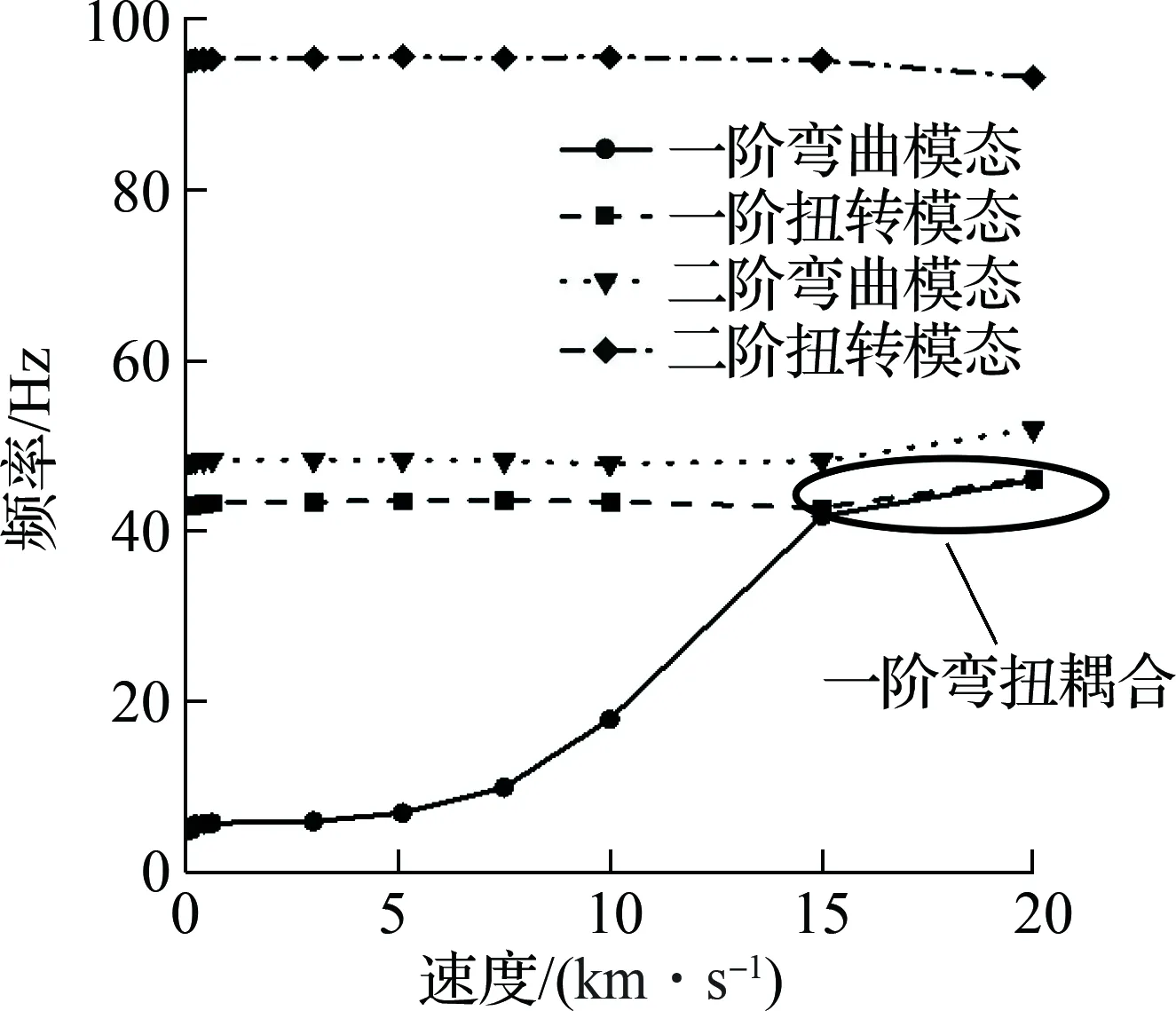
以热颤振现象出现最早的工况(飞行高度20 km,马赫数8)为例,高温下机翼结构在约4.638 5 km/s处发生颤振失稳,相较于常温下6.302 5 km/s颤振边界,降低了26.4%.根据对应的速度-频率图判断系统的颤振失稳表现形式,如图8所示.可看出,颤振失稳表现形式为一阶弯扭耦合.为提高机翼热颤振边界,有必要对机翼结构进行气弹剪裁优化,以降低气动力热耦合效应的不利影响.

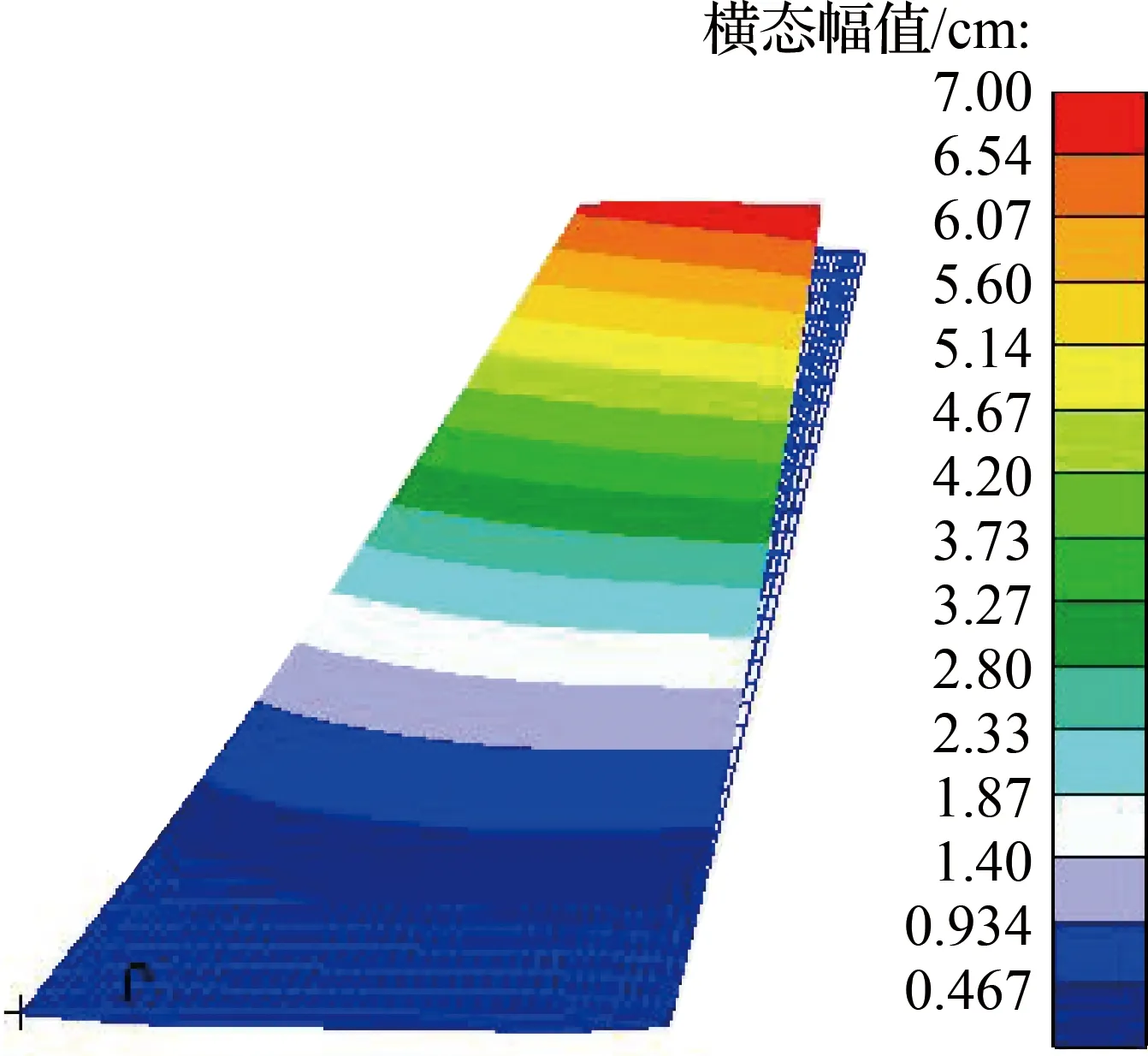
(a) 一阶弯曲(常温,10.658 Hz)

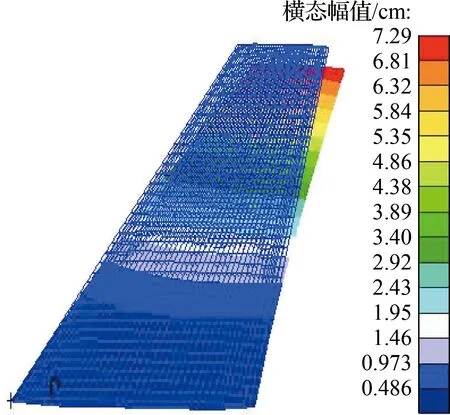
(b) 一阶弯曲(高温,10.325 Hz)

(c) 一阶扭转(常温,43.450 Hz)

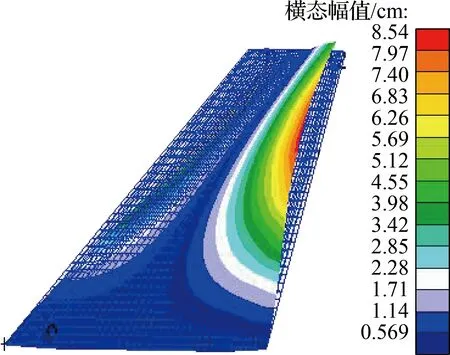
(d) 一阶扭转(高温,41.423 Hz)

图7 不同飞行工况下速度-阻尼曲线

3 复合材料机翼热气弹剪裁及软件开发

3.1 静强度约束

在机翼气弹剪裁设计初期,尽管满足热颤振约束条件至关重要,但静强度约束仍不可忽略,这关系到结构是否能满足服役所需的高强度要求.以典型层合板为例,其受力分布见图9.图中,Nx、Ny和Nxy分别为层合板横截面在x方向、y方向和xy方向单位长度上的力;Mx、My和Mxy分别为层合板横截面在x方向、y方向和xy方向单位长度上的力矩.

(a) 常温

(b) 高温

图9 层合板力以及力矩示意图

假设层合板在x、y、z三个方向上的位移分别为u、v、w,并以数字1、2和6分别代表x、y和xy方向.根据胡克定律和经典层合板理论,层合板中第k层板的应力应变可表示为

(6)

4Q66sin2θkcos2θk+Q22sin4θk

(7)

Q12(sin4θk+cos4θk)

(8)

4Q66sin2θkcos2θk+Q22cos4θk

(9)

(Q12-Q22+2Q66)sin3θkcosθk

(10)

(Q12-Q22+2Q66)sinθkcos3θk

(11)

Q66(sin4θk+cos4θk-2sin2θkcos2θk)

(12)

(13)

式中,E1和E2分别为x方向和y方向上的材料弹性模量,Pa;G12为材料的剪切模量,Pa;v12和v21为材料泊松比.

由于在高超声速服役工况下,气动热载荷对结构应变的影响不可忽略,故考虑结构的热膨胀应变,有

εi=εi,0-εi,T

(14)

式中,εi,0为常温下结构的应变;εi,T为高温热载荷引起的热膨胀应变.引入热膨胀系数αi,结构的热膨胀应变可表示为

(15)

复合材料薄板第k层板的力Ni,k和力矩Mi,k可被定义为

(16)

(17)

式中,h为层合板厚度,mm.联立式(6)、(16)和(17),可得

(18)

式中,ε为面内应变矩阵;K为弯曲应变矩阵;A、B、D分别为面内刚度矩阵、耦合刚度矩阵、弯曲刚度矩阵.对应的矩阵求解表达式如下：

结构在主方向上的应力分量可大致分为纵向拉伸/压缩、横向拉伸/压缩和面内/层间剪切.考虑到层合板内力和弯曲之间可能存在耦合作用,在进行铺层设计时,要尽可能采用对称铺层设计来消除面内耦合刚度.同时为保证材料在静强度下不被破坏,根据强度失效准则,材料主方向任一应力分量均不得超过设计的最大许用值.

3.2 气动弹性分析系统研发

基于C/C++开源语言环境搭建复合材料机翼气动弹性优化设计软件平台(Aero-Opt),软件主界面如图10所示.软件包含模型建模、网格划分等前处理功能,以及变参分析、模态振型显示和气弹剪裁优化等后处理模块.因篇幅限制,本文重点介绍气弹剪裁优化模块.

图10 Aero-Opt软件主界面

在软件的气弹剪裁优化模块中,用户可根据实际工况自定义选择静强度约束、颤振约束或静强度与颤振联合约束[17-19];将铺层层数、铺层角度以及铺层顺序作为设计变量,以质量最优作为目标函数;采用遗传算法进行铺层全局优化,为避免出现局部最优的情况,对每一代种群优化铺层角度前判断是否先优化铺层层数,以达到提前优化种群基因长度的效果,提高气弹剪裁优化效率.结构优化数学模型可表示为

s.t.g(Xn,Yn)≥Ddesign1≤n≤30,n∈N+

minM(X,Y)

Xn∈{±45°,0°,90°},Yn∈{0,1}

式中,Xn为第n铺层的铺层角度,设计的最大铺层层数不超过30,铺层厚度为2 mm;Yn为1时表示第n层板存在,为0时表示不存在;g(Xn,Yn)为当代每个种群计算出的设计值;Ddesign为约束条件.M(X,Y)为优化目标函数,以满足约束条件前提下的最小质量视为最优.

为了提升高超声速飞行器的热颤振边界,对气动力热耦合效应最恶劣的飞行工况(飞行高度20 km、马赫数8)下的复合材料机翼蒙皮进行气弹剪裁优化.在软件平台对应模块中输入适当的约束条件：纵向拉伸/压缩应力均为2.56 GPa、横向拉伸/压缩应力均为150 MPa、面内/层间剪切应力均为50 MPa,颤振速度不低于5 km/s,优化模块数设为1,最大铺层层数设为15,对应的初始质量为1 848 kg,热颤振边界为4.638 5 km/s.然后输入遗传优化算法参数：种群大小设为20,遗传代数设为50,代沟设为0.9,交叉概率和变异概率分别设为0.7和0.01.设置好变量后,即可开始优化流程.软件运行日志栏会实时显示每代各个种群的最小颤振速度、最优质量、主方向上应力与最大许用应力的差值等信息.

最终优化收敛结果如图11所示,目标函数在第16代时达到收敛.模型经过气弹剪裁后的铺层层数为8;铺层角度和顺序为0°,0°,-45°,45°,0°,-45°,-45°,90°;优化后的模型热颤振速度为5.676 9 km/s,质量为1 556.8 kg;与初始模型相比,热颤振边界提高了22.4%,质量降低了15.76%.

图11 收敛曲线和优化结果

4 结论

1) 气动热载荷分布表明,机翼前缘热流密度最大,并向后缘逐渐递减.通过与K-R经验公式求解的驻点处热流密度作对比,验证了仿真计算的正确性.

2) 对比机翼在常温和高温下的一阶弯扭模态发现,气动热效应会使得结构固有频率降低,振型幅值增大.

3) 根据经典颤振理论得到的热颤振结果表明,机翼颤振表现形式为一阶弯扭耦合.考虑到复材机翼的可设计性,对机翼进行含颤振约束的气弹剪裁优化,优化后结构质量降低了15.76%,热颤振边界提高了22.4%.

4) 基于C/C++开源语言环境开发Aero-Opt自主工业化软件,集成了气弹优化的典型分析模块,为高速飞行器前期优化设计提供有效借鉴.