桥面临时设施作用下大跨悬索桥主梁涡振性能及表面风压分布

郎天翼 王 浩 贾怀喆 刘震卿 徐梓栋 郜 辉

(1东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 211189)(2华中科技大学土木与水利工程学院, 武汉 430074)(3内蒙古科技大学建筑与土木工程学院, 包头 014010)

涡激振动(简称涡振)是一种限幅振动，兼具自激和强迫振动性质，虽然不会对结构造成瞬时的失稳破坏，但长时间的大幅振动将使结构发生疲劳损伤，缩短桥梁的使用寿命，影响桥梁的健康运营[1-2].此外，桥梁的涡振还会影响桥上行车安全性及舒适性，引发社会对桥梁安全的负面关注.为有效控制桥梁涡振，应掌握不同运营环境下桥梁的涡振机理.

目前，针对桥梁涡振机理的研究主要从主梁表面旋涡演化规律及风压分布特性入手，采用现场实测[3]、风洞试验[4-5]、数值模拟[6]等研究方式.虽然现场实测是桥梁涡振研究中最直接的手段，但由于涡振是一种偶发现象，无法利用现有桥梁进行常态化研究.风洞试验通过同步测压技术研究主梁涡振时的表面压力分布状况[4]，利用粒子呈像技术(particle image velocimetry, PIV)[5]揭示结构的动力特性及流场的演变过程.但在风洞试验中模型制作、参数调试需要的物理时间成本较高，且获取的数据有限.随着计算机性能的不断提升，数值模拟中计算流体动力学(computational fluid dynamics, CFD)方法也逐渐成为研究结构风工程的有效手段，通过对结构模型及风环境的等效模拟，可完整反映流固耦合的全部特性，且便于提取整个计算域中的风场数据，是研究主梁涡振机理的理想工具.祝志文等[7]基于CFD的方式，探究了扁平箱梁节段模型的棱角误差对气动力和涡脱特性的影响.陈星宇等[8]利用CFD技术，研究了中央开槽宽度对箱梁涡振特性的影响.

然而，在进行桥梁涡振研究时，需采用有效的数据处理方法揭示流场特征，其中本征正交分解(proper orthogonal decomposition, POD)法受到了风工程领域学者们的广泛关注.Armitt[9]首先将POD法应用于风工程领域，探究了冷却塔表面的风压波动特性.Bienkiewicz等[10]采用POD法分析了建筑屋盖的表面压力分布特征.胡传新等[11]利用POD法对涡振时拱肋断面的表面压力进行研究，得到了引发涡振的主要压力波动区域及分布.马凯等[12]基于CFD手段和POD法分析了矩形断面的涡振现象，结果表明数值模拟结果与POD分析结果相符，且与涡振机理研究互补.综上，在数值模拟结果的基础上利用POD法有利于分析主梁表面旋涡的演化规律及风压分布特性，为深入探究涡振机理提供了有效的途径.

目前，在主梁涡振的影响因素研究中，关于防撞护栏、扶手栏杆、检修车轨道的研究较多[13-15]，对临时设施的研究较少，尚未形成统一认识[1-2].而在近期的桥梁运营中，出现了临时设施引发主梁涡振的现象[16]，造成桥梁关闭并引发广泛的社会舆论.因此，有必要探究临时设施对主梁涡振的影响，进而保证桥梁的安全运营.

鉴于此，本文以某大跨悬索桥为研究对象，采用计算流体力学方法进行主梁涡振模拟，研究了临时设施致主梁涡振全过程的风场演化规律，并利用本征正交分解法分析了主梁涡振时表面风压时空分布特征.研究结果在一定程度上揭示了临时设施作用下主梁涡振机理，为大跨度桥梁健康运营提供了理论基础和保障.

1 主梁节段数值模型

1.1 模型参数

图1给出了某大跨悬索桥主梁的基本尺寸.施加临时设施前，主梁为流线型扁平钢箱梁，主梁宽36.9 m，梁高3.0 m.为研究临时设施对主梁涡振的影响，在迎风侧上游设置临时设施，临时设施高1.2 m，宽度为0.2 m.

图1 主梁断面示意图(单位: m)

主梁结构的一阶竖弯频率为0.133 7 Hz，等效质量为26 676 kg/m.数值建模时，对实桥的动力学参数采用一定的相似比进行缩放，实桥及数值模型的主要动力学参数见表1.

1.2 计算域网格及边界条件

采用嵌套网格的方式实现网格运动.图2给出了计算域、边界条件及组分网格所在区域.计算域尺寸的选取参考文献[17]，其中背景网格的长度为24B(B为数值模型中主梁宽度)，高度为12B，下游网格到组分网格区域中心的距离为18B.图3进一步给出了裸桥断面和含临时设施时的组分网格，网格尺寸为4B×3B，2种断面形式的阻塞率分别为0.67%和0.95%.

在组分网格中，主梁模型周围设置0.027B厚度的边界层，边界层的首层网格高度为6.78×10-5B，网格增长率为1.05.为保证网格平稳过渡，在边界层外围设置了非结构网格矩形过渡区域，过渡区域的尺寸为1.36B×0.41B，过渡区域边界到组分网格边界采用计算效率较高的结构网格进行划分(见图3).裸桥断面的网格数量为229 695，含临时设施的网格数量为241 229，背景网格中网格总数为86 795.

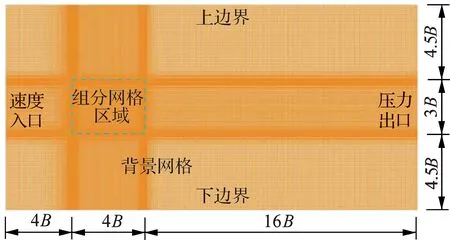
图2 计算域及边界

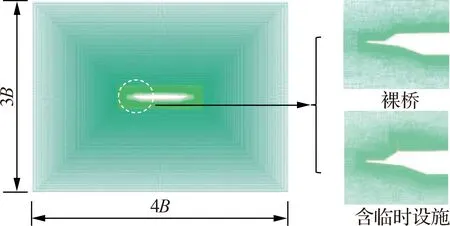
图3 组分网格及主梁断面形式

计算域左侧为速度入口，右侧为压力出口，出口压力为标准大气压；上下两侧设置为对称边界，主梁模型表面为无滑移壁面边界.采用瞬态求解方式，计算时间步长为1 ms，湍流模型选用SST剪切应力运输模型，离散格式为二阶迎风格式，并采用速度-压力耦合的Coupled算法.2种断面形式下主梁表面的无量纲壁面距离值基本都小于1，最大值不超过2，满足所选用的湍流模型对边界层的要求.

1.3 数值模拟结果验证

为了验证数值模型的准确性，图4对比了风速15.0 m/s时裸桥断面三分力系数的数值模拟与风洞试验结果.体轴坐标下三分力系数定义如下：

(1)

(2)

(3)

式中，Cx、Cy分别为x、y方向上的气动力系数；CM为扭转气动力系数；Fx、Fy分别为二维主梁断面受到的x、y方向作用力；Mxy为主梁受到的沿主梁轴向的扭力；ρ为空气密度；v为来流风速；H为数值模拟中主梁的高度.

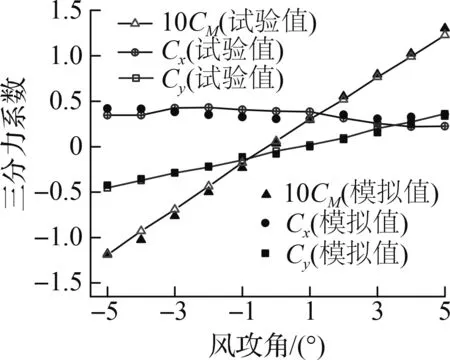
图4 三分力系数图

由图4可知，当风攻角为-5°～5°时，三分力系数的数值模拟结果与风洞试验结果变化趋势一致，升力系数、扭力系数数值上吻合良好.鉴于风洞试验和数值模拟断面无法避免的差异以及风洞试验的测定不确定性，数值模拟的阻力系数与风洞试验结果稍有偏差，但仍在合理范围内.

2 风场流态分析

2.1 临时设施作用下的主梁涡振数值模拟

图5给出了临时设施作用下主梁涡振的风速锁定区间.由于临时设施的搭建破坏了主梁断面的流线型形式，当风攻角为0°、风速为7.0～10.0 m/s时会诱发主梁断面发生涡振现象.

选取来流风速为8.0 m/s的工况，该风速在主梁涡振风速锁定区间内.如图6(a)所示，主梁的竖向位移响应幅值逐渐增大，一段时间后，位移响应达到稳定状态.涡振稳定时，主梁振动的频率分布见图6(b).由图可知，振动响应的卓越频率 10.632 Hz与结构的固有频率10.672 Hz基本保持一致.

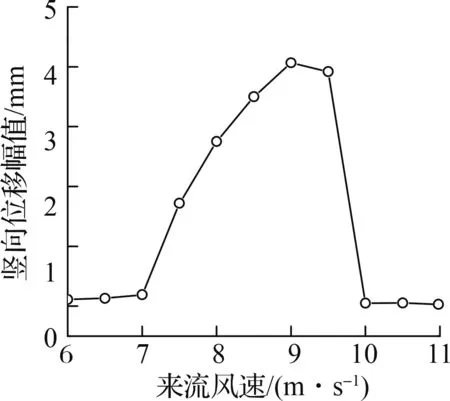
图5 临时设置致主梁涡振的风速锁定区间

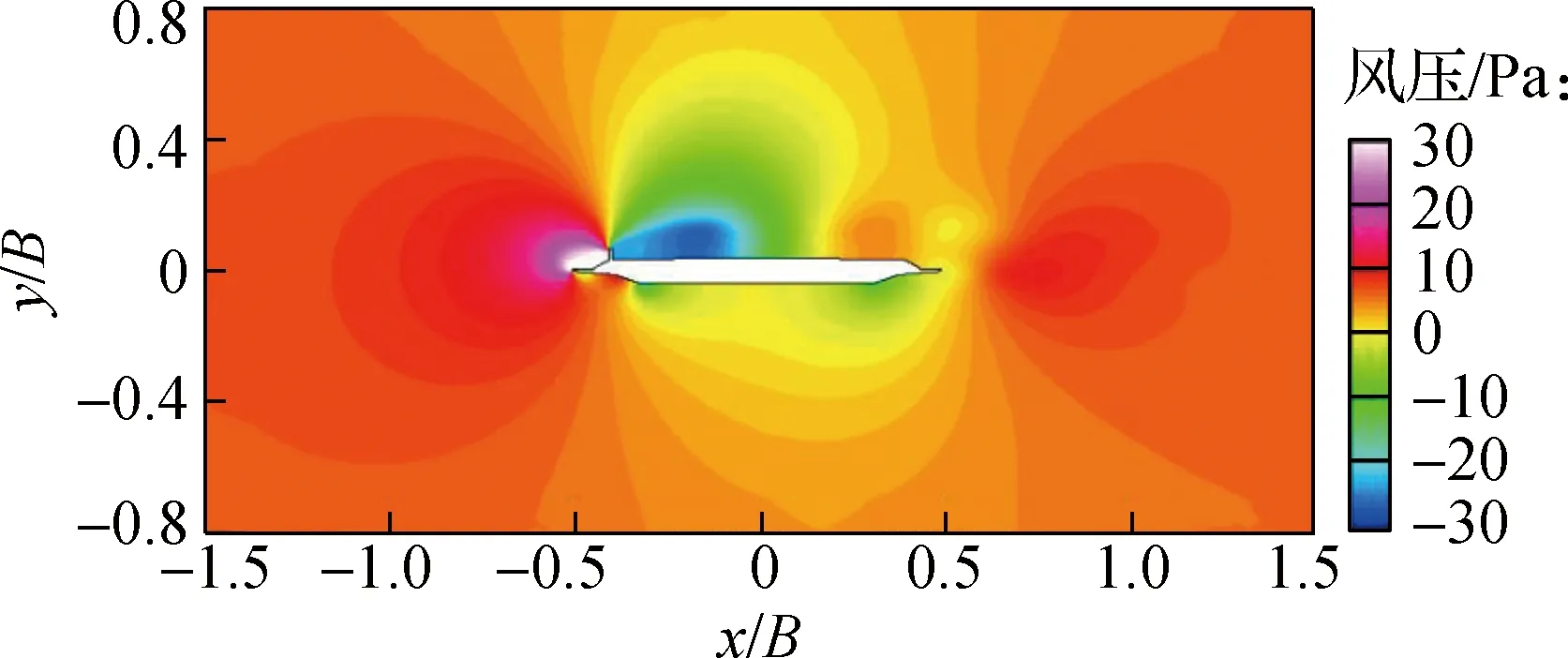
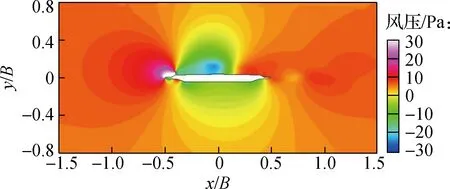
图7给出了主梁涡振达到稳定状态后一个周期内时间间隔为1/4T(T为振动周期)的主梁周围流场压力云图和流线图，以分析压力场变化与旋涡演变对主梁涡振的影响.由图可知，临时设施的加入导致了显著的流动分离现象，在主梁上方生成较大的旋涡.在一个振动周期内，旋涡相继经历了生成、分离、再附着和脱落的演变.流场的演变导致作用在主梁表面压力产生周期性变化，进而驱动主梁振动.

(a) 竖向位移响应

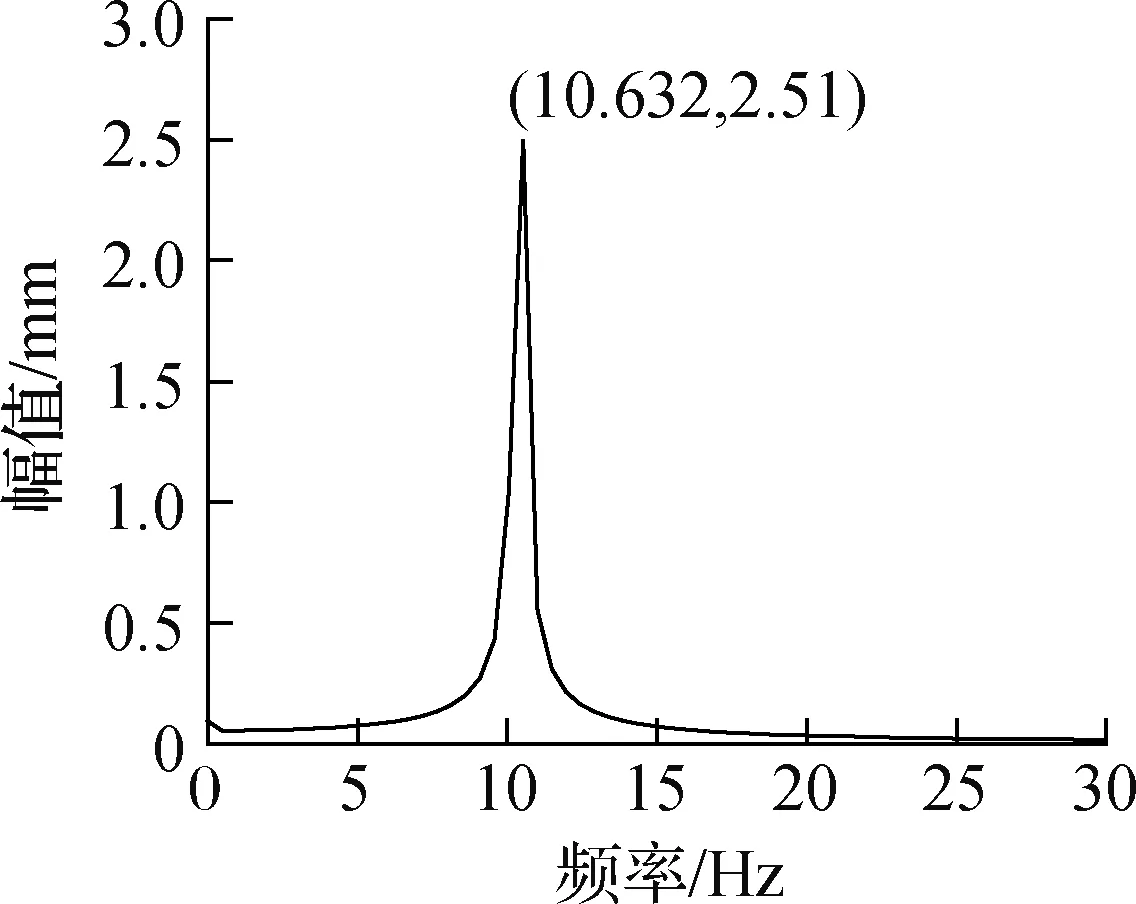
(b) 频谱图

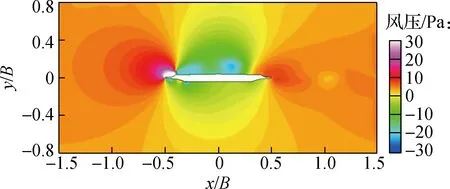
(a) t=0时流场压力云图

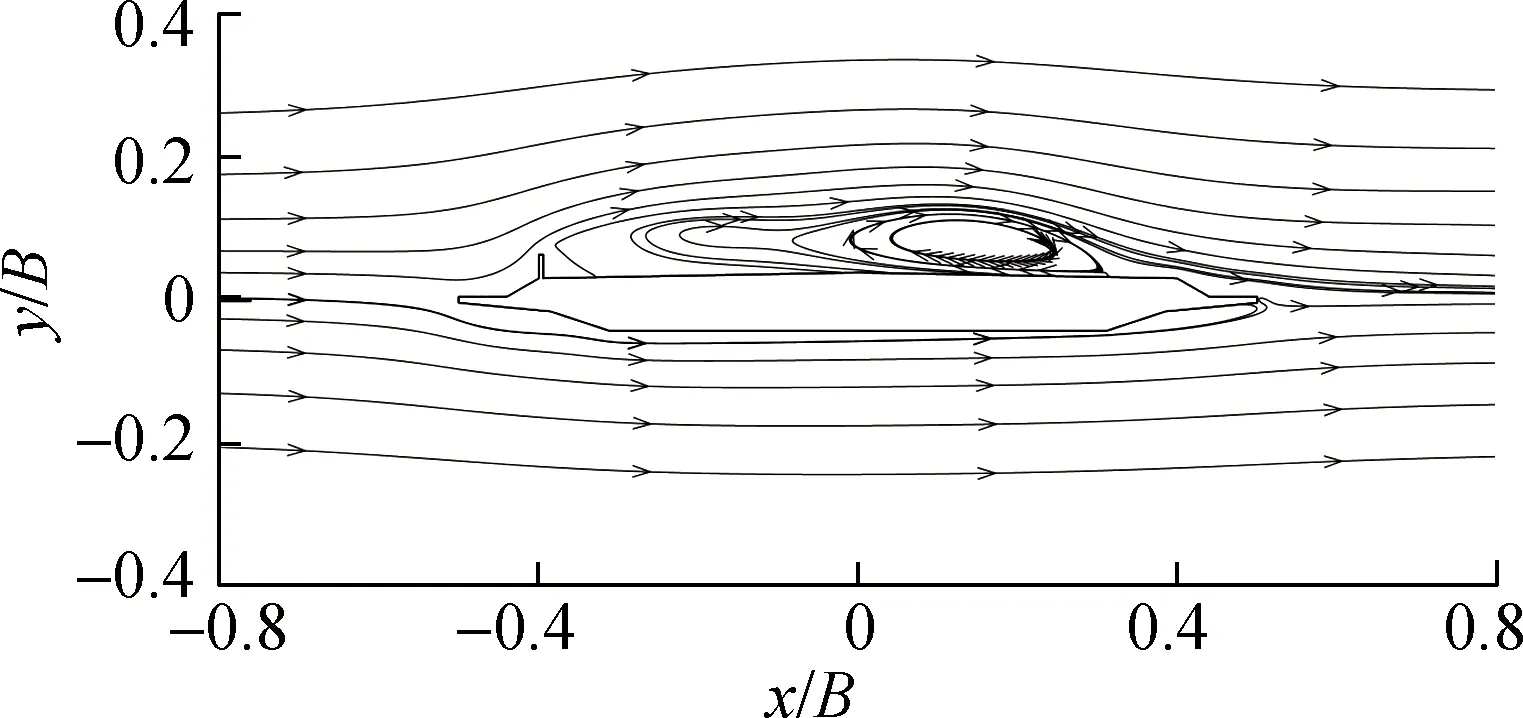
(b) t=0时流线图

(c) t=0.25T时流场压力云图 (d) t=0.25T时流线图

(e) t=0.5T时流场压力云图 (f) t=0.5T时流线图

(g) t=0.75T时流场压力云图 (h) t=0.75T时流线图

(i) t=T时流场压力云图 (j) t=T时流线图

由图7可知，当主梁运动时刻t=0时，主梁断面运动到振动的中心位置，上一周期的旋涡移动到主梁顶板下游，新的旋涡还未生成.当t=0.25T时，主梁断面运动到一个周期内的波峰位置，由临时设施导致的大型负压场旋涡逐渐生成，旋涡中心作用在顶板上游区域，上一周期产生的旋涡附着到顶板尾部，并扩展到腹板、人行道板上方区域.当t=0.5T时，主梁断面运动到振动中心位置，旋涡向顶板下游扩展，旋涡具有分离趋势，上一周期产生的旋涡于主梁尾部人行道板处发生脱落；同时，负压场逐渐缩小，负压极值下降.当t=0.75T时，主梁断面运动到周期内的波谷位置，此周期内产生的旋涡分离，并向顶板下游移动，旋涡中心移动到顶板中游区域，且负压场继续缩小.当t=T时，主梁断面回到振动中心位置，旋涡移动到主梁顶板下游，新的旋涡还未生成.主梁结构周围旋涡的形成和发展过程与已有的涡振数值模拟结果一致[18]，说明桥面上游结构对旋涡的形成和脱落具有重要影响.

2.2 裸桥断面风荷载数值模拟

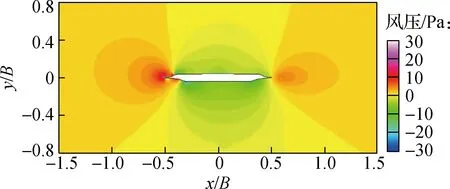
无论是风洞试验还是数值模拟，裸桥断面在风环境中均未发生涡振现象，说明本研究选用的桥梁主梁气动外形较好，规避了涡振的潜在风险.采用与2.1节相同的试验条件，观察主梁周围流场的形态.计算稳定时主梁周围流场状态见图8.构造折点引起流动分离，在主梁周围会产生局部的小尺度旋涡.然而，旋涡尺寸均较小，且分布规则，尺寸、位置随时间几乎无变化，故对主梁的动力性能影响较小.

2.3 临时设施作用下的主梁未涡振数值模拟

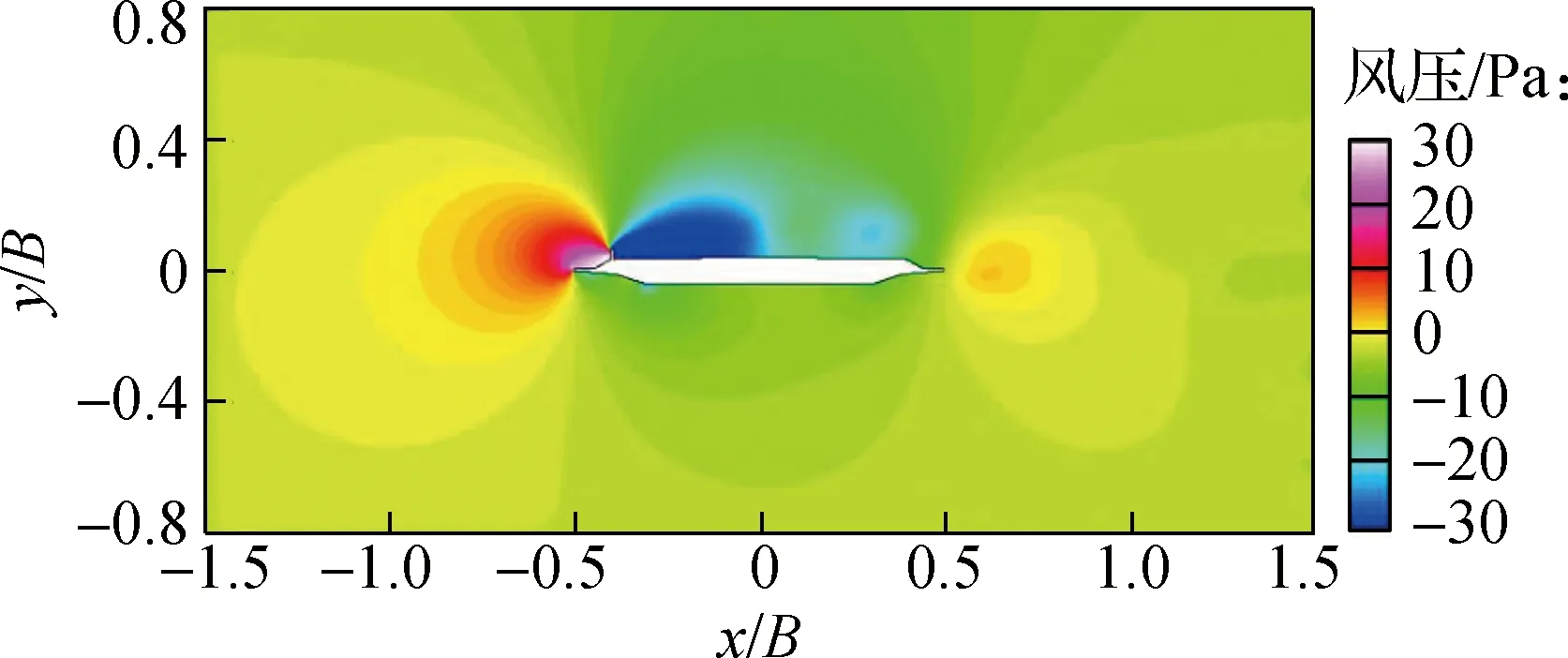
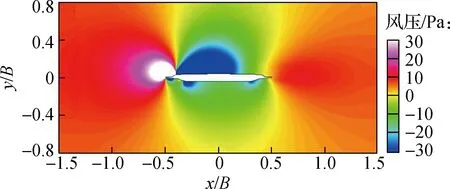
为观察临时设施未致涡振时主梁周围流场的形态，设置风攻角为0°，风速为16.0 m/s.由图5可知该风速不在涡振风速锁定区间内，此时主梁未发生涡振现象.受临时设施的作用，流动分离点比较明确，计算稳定时主梁周围流场状态见图9.由图可知，在临时设施的迎风区域和背风区域分别生成了较大的正压场和负压场，主梁断面顶部生成一个大型旋涡，同时在构造折点作用下，上、下游人行道板两侧均生成许多小型旋涡.但这些旋涡的尺寸、位置随时间几乎无变化，主梁的动力性能保持相对稳定.

(a) 流场压力云图

(b) 流线图

(a) 流场压力云图

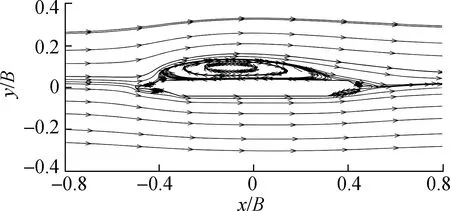
(b) 流线图

3 基于POD法的主梁表面风压分布

3.1 表面压力提取

风洞试验中利用动态测压技术，可收集指定位置的风压数据[12]，在数值模拟中能够更加便捷地提取及处理数据.数值计算时主梁表面共设置95个测点(编号为S1～S95)，以反映主梁表面的压力分布情况，测点布置见图10.裸桥断面及含临时设施时的测点布置情况一致，主梁表面测点压力的采样周期(即数值模拟时的计算时间步长)为1 ms.

图10 主梁表面压力测点布置图

利用自定义函数(user-defined function, UDF)提取测点风压数据时，首先提取桥梁整个节段模型二维断面上的风压时程数据，主梁表面网格单元划分的数量即为风压时程数据的维度；然后，确定测点所在单元及排序；最后，在完备的风压时程数据中找出对应测点单元对应维度的数据，从而完成对测点风压时程数据的提取.

3.2 本征正交分解法

POD法是一种将多元数据降维处理的方法.利用POD法描述结构表面风压分布时，风压时程数据被分解为多阶本征模态及所对应的特征值(即本征值).本征模态包括依赖空间的本征向量和依赖时间的演化序列，各阶本征向量相互正交，表示各阶模态下的风压分布，本征值则表示各阶模态所捕获的能量.各阶模态中的风压分布反映了主梁表面的风压脉动情况，绝对值较大的部分表示该区域风压波动较大，反之则说明该区域风压波动较小[13,19].

3.3 主梁涡振时的表面压力分布

对2.1节中主梁涡振时的表面风压数据进行本征正交分解，得到前4阶模态的风压分布及频率成分，结果见图11.由图可知，在第1阶模态中，主梁上游区域、下游区域和下游人行道板区域风压波动较大，而主梁底板及下游腹板范围内风压波动很小.结合涡振发生过程中的流场压力云图可知，临时设施导致的涡脱及再附着现象与第1阶模态的风压分布规律一致，主梁顶板上游区域、下游区域承受最大的旋涡作用，且风压场对上下底板的作用力方向一致.而在上游人行道风嘴、人行道板和腹板交接处及腹板和底板交接处，构造折点引起的流动分流导致存在一定的风压波动，但不构成对涡振的主要贡献.在第2阶模态中，风压波动集中在底板、下腹板和下人行道板区域，顶板中下游区略有波动，但顶板与底板的风压作用力方向相反.在第3阶模态中，顶板下游和底板下游的风压波动较为明显，上、下游风嘴处的波动也同样显著.

(a) 第1阶模态风压分布

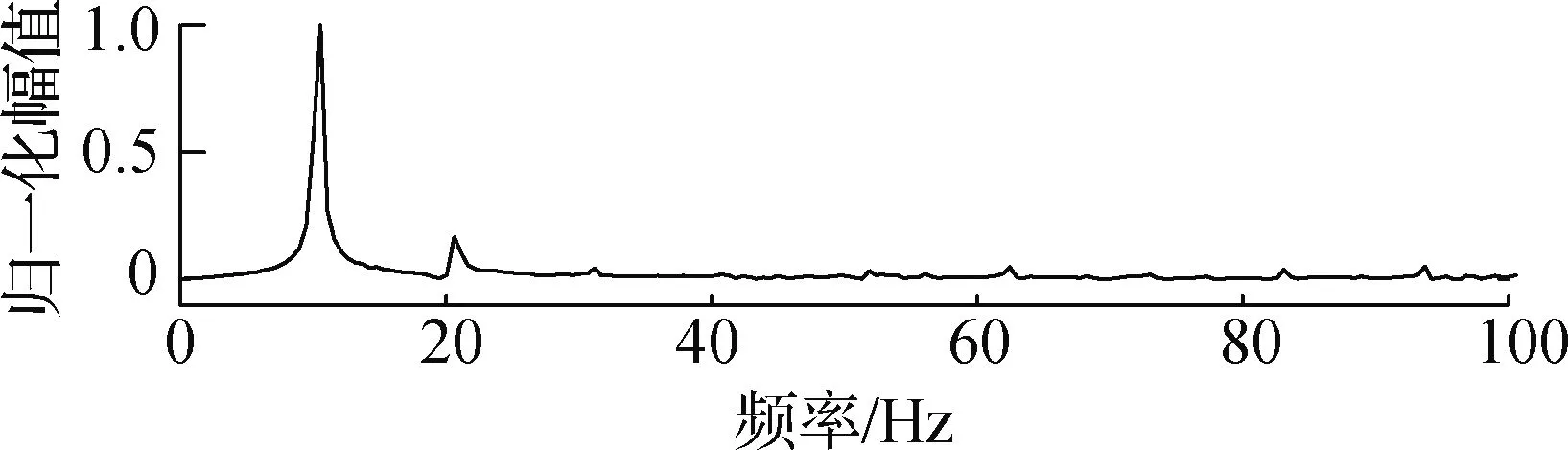
(b) 第1阶模态频率成分

(c) 第2阶模态风压分布

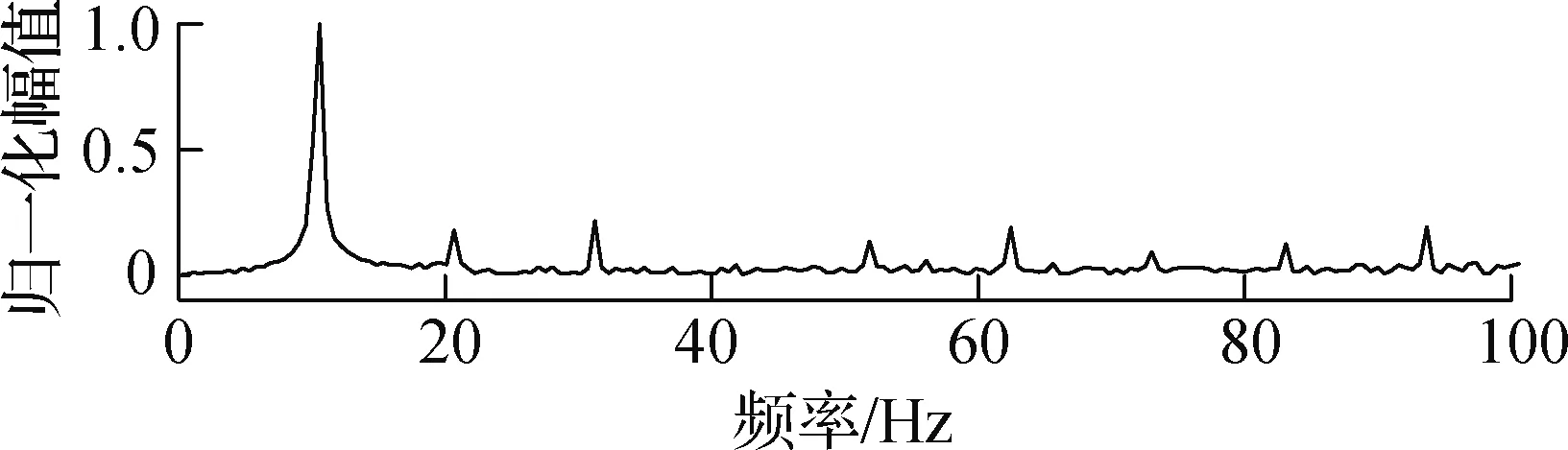
(d) 第2阶模态频率成分

(e) 第3阶模态风压分布

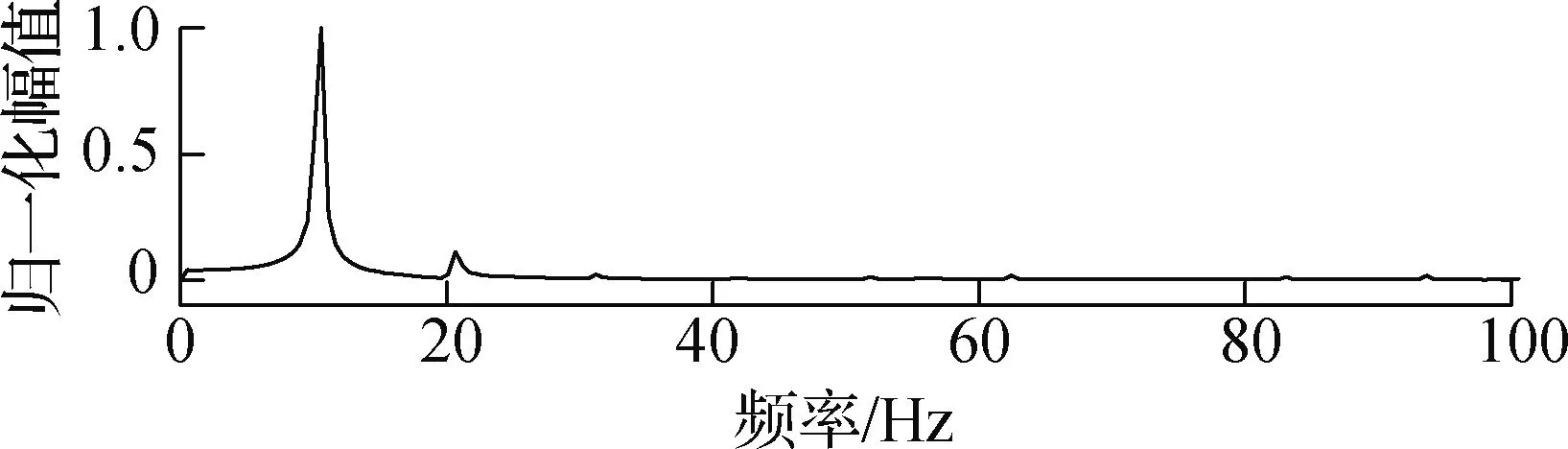
(f) 第3阶模态频率成分

(g) 第4阶模态风压分布

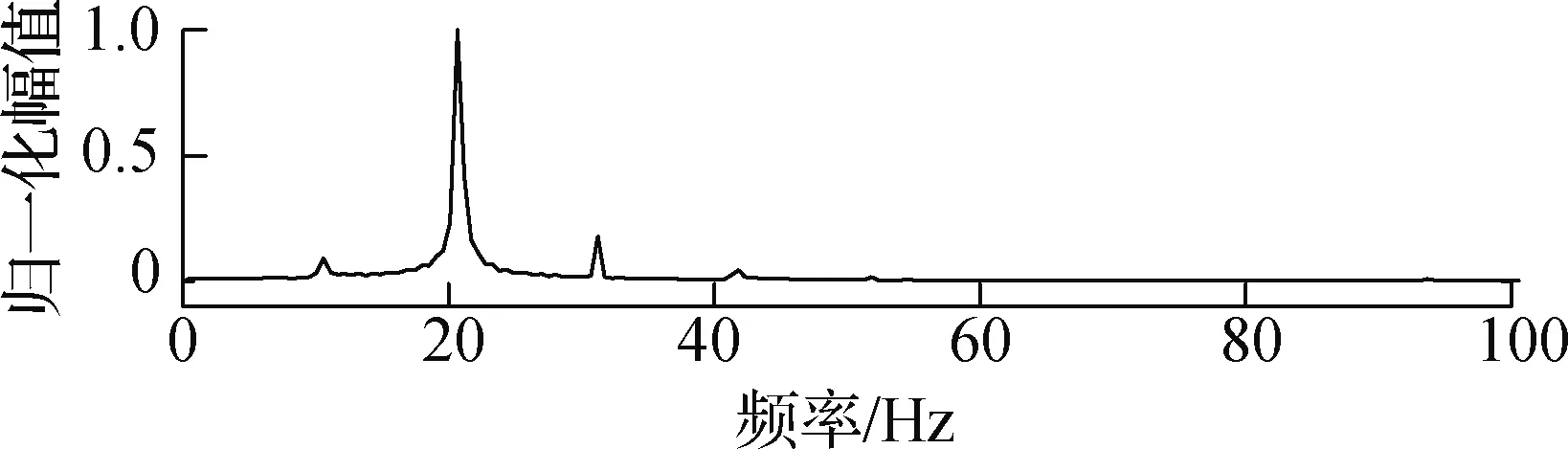
(h) 第4阶模态频率成分

由图11可知，前3阶模态能量分别占总能量的38.7%、29.6%和28.1%，且其主频、涡振频率及主梁固有频率一致，说明前3阶模态对主梁涡振的贡献占据主导地位.而第4阶模态能量仅占总能量的2.3%，且卓越频率为20.635 Hz，与结构固有频率相差较大，说明其对主梁涡振的贡献很小.由此可知，前3阶模态是引发主梁涡振的主导模态，从第4阶起的本征模态对主梁涡振的贡献可忽略不计.

4 结论

1)当来流风速为7～10 m/s时，临时设施会引发流动分离，主梁顶部形成了较大尺寸的旋涡.一个周期内，旋涡相继经历了生成、分离、再附着和脱落的演变，流场的变化驱动着主梁发生涡振现象.

2)主梁涡振发生时，其表面风压脉动的本征模态中存在涡振主导模态，且主导模态的卓越频率与结构的固有频率一致，而非主导模态的卓越频率与固有频率相差较大，对涡振的贡献较小.受临时设施的影响，本征模态中主梁表面风压波动主要集中在顶板区域.

3)由于裸桥断面具有较好的流线型气动外形，构造折点影响下仅产生小尺寸旋涡，并不能引发主梁涡振.含临时设施但未涡振时，临时设施导致主梁顶部产生较大旋涡，未发生旋涡分离等现象，主梁的动力性能保持相对稳定.