嵌套网格技术在悬索桥扁平钢箱梁气动参数识别中的应用

温学华 王 浩 张 寒 徐梓栋 陶天友

(东南大学混凝土及预应力混凝土结构教育部重点实验室， 南京 211189)

随着计算机科学技术的蓬勃发展，计算流体力学(computational fluid dynamics, CFD)数值模拟技术也在不断进步.CFD自应用到桥梁风工程以来，凭借网格的多样性，在结构风工程领域中得到了广泛应用[1].

目前，在桥梁风工程的数值模拟领域经常使用的是传统的静网格与动网格技术[2].对于仅创建单一网格的工程应用情况下，传统网格技术在工作量上与动网格技术相差不大.然而，在同一个工程应用情况下，需要同时用到同一个截面的静网格和动网格，嵌套网格所需求的工作量相比传统网格大幅减少，从而达到提高工作效率的目的.此外，对于常见的工程动态模拟工程(如颤振导数识别问题)，往往需要使用动网格技术.动网格常用方法包括网格变形、滑移边界、网格再生等.随着待处理运动部件的运动幅度增大，传统网格技术调整难度急剧增加[3].嵌套网格中每一个子流域互相独立又互相嵌套，流域中的物体可以带着其相关子网格一起运动，从而达到物体运动的数值模拟[4].这一特点使得嵌套网格并不涉及网格的再生与变形问题，从而有效避免动网格模拟中出现负体积，提高了模拟精度.

本文以某大跨度悬索桥为工程背景，基于CFD与嵌套网格技术，对悬索桥扁平钢箱梁断面静力三分力系数和颤振导数进行数值模拟，并将结果与传统网格模拟结果进行对比，以验证基于嵌套网格方法的数值分析的可靠性.

1 主梁断面气动特性

1.1 静力三分力系数

由平均风作用引起的静荷载被称为静力风荷载.在流速为U、风攻角为θ的均匀流体中，桥梁断面将受到阻力FD、升力FL以及来流导致的静力矩MT作用.在风轴坐标系下，主梁断面的静力三分力如图1所示.

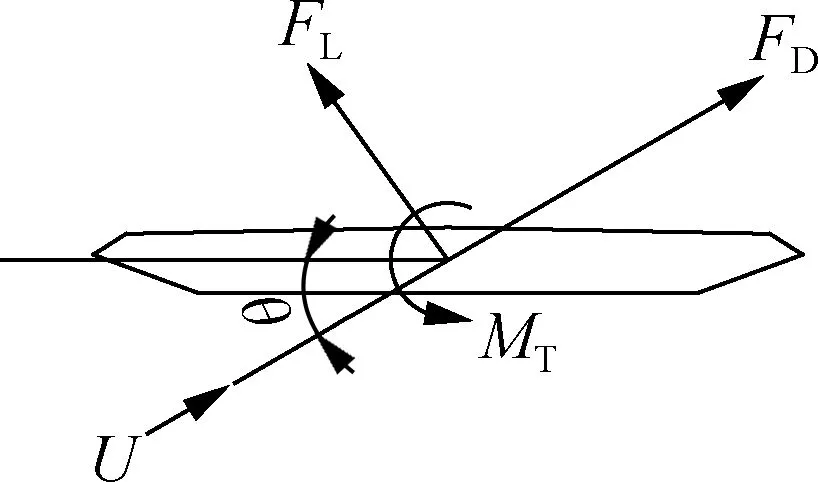
图1 风轴坐标系下静力三分力示意图

主梁断面阻力系数为[5]

(1)

升力系数为

(2)

升力矩系数为

(3)

式中，ρ为空气密度；B、D分别为主梁断面宽度和高度.

1.2 颤振导数

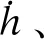
(4)

(5)

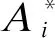
2 基于嵌套网格技术的流域建模

嵌套网格也被称为重叠网格[7].利用嵌套网格可以解决复杂流场域和流动变化大的区域中的网格生成问题.网格生成方法主要包含分解计算网格和合并网格2个部分[8].首先，将待解计算域人为划分为2个及以上的子流域，这些子流域间不仅可以使用同一个边界，也可以发生重叠，但要求每个子区域都应具有独立性；然后，对生成的子区域进行预处理，删除整个网格中相互交叠的多余网格单元；最后，在嵌套网格边界建立每一个子流域之间的变量传递关系，得到由各子流域组成的完整网格，即为嵌套网格[9].

对于完整的嵌套网格，每一个子流域都可采用不同求解器进行独立求解.通过各子流域边界插值，耦合形成流场整体信息，进而得到整个嵌套网格流域的流场分布.

2.1 工程背景

本文研究对象为某长江大桥.主梁采用近似理想二维平板的扁平闭合流线型钢箱梁截面.其施工状态主梁断面布置见图2.

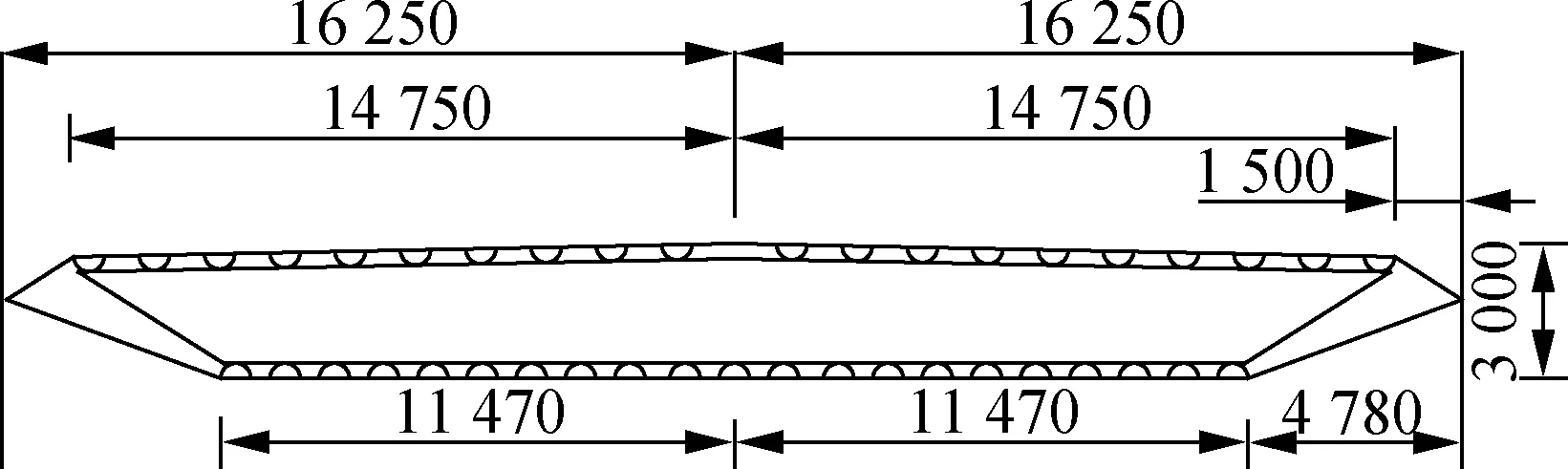
图2 某大跨度悬索桥施工状态主梁断面图(单位：mm)

选取该大跨度悬索桥施工状态作为本文研究对象，建立几何缩尺为1∶50的计算模型[10].模型宽度B=650 mm.

2.2 背景网格建模

选取长24B、宽16B的计算领域.其左侧为风速入口边界，湍流强度设定为0.5%，湍流黏性系数比值设定为2.0[10]；右侧为零压力出口边界，湍流的设置与入口处保持一致；上下两侧均设定为对称边界.待试验断面几何中心离流域上下边界距离均为8B，离入口、出口距离分别为8B和16B[10]，主梁断面表面设定为无滑移.背景网格中间加密区网格高度取16 mm，最大网格尺寸为0.2 m.湍流模型为RNGk-ε模型[11]，其中k和ε分别为紊流脉动动能及其耗散率.计算域布置见图3.

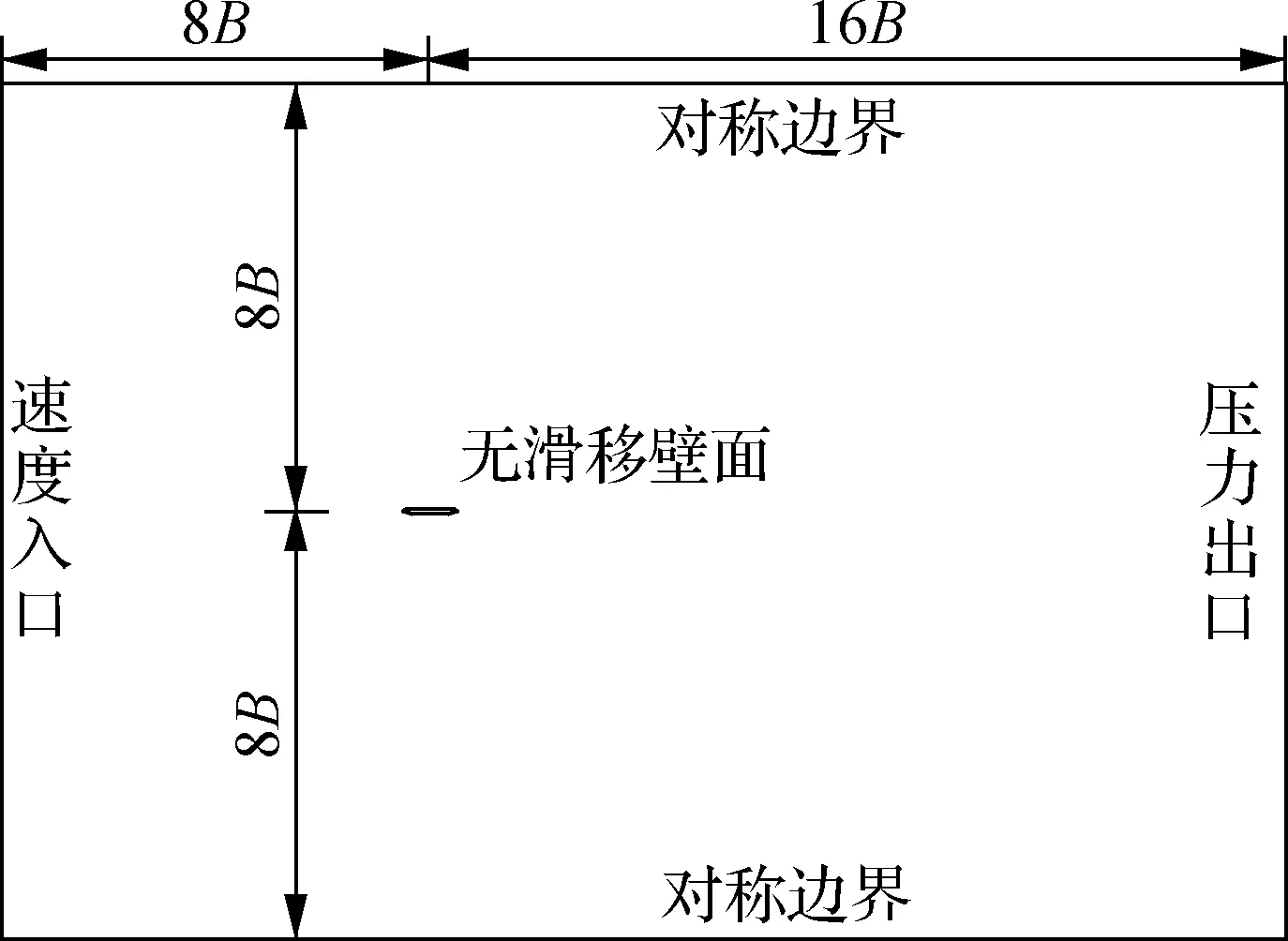
图3 计算域布置图

2.3 中心网格建模

本文使用RNGk-ε模型和标准壁面函数.参考文献[12-13]，对于待试验主梁断面附近的中心网格，第1层网格高度取为0.8 mm，最大网格尺寸为16 mm, 两者之间网格尺寸均匀过渡.采用结构网格，网格形式为规则四边形网格加不规则四边形网格.嵌套网格的组分网格划分见图4.将背景网格和组分网格进行嵌套，得到的悬索桥主梁断面网格划分如图5所示.研究三分力系数与风攻角之间的关系时，相较于传统网格需要重新划分一整套网格，嵌套网格则只需对中心网格进行整体旋转后与背景网格嵌套.

2.4 传统网格建模

本文选取结构网格，基于ICEM CFD软件中

图4 组分网格

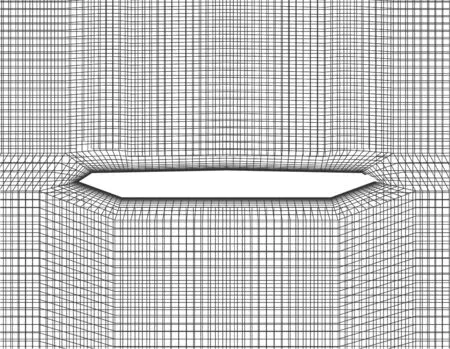
图5 嵌套区域网格嵌套图

的Block功能进行传统网格划分.近壁面采用标准壁面函数[14]进行处理，第1层网格高度取1.2 mm，最大网格尺寸为0.4 m；网格形式为规则四边形网格加不规则四边形网格；传统网格所用计算域、湍流参数以及湍流模型均与嵌套网格相同.悬索桥主梁断面传统网格划分见图6.

(a) 整体网格

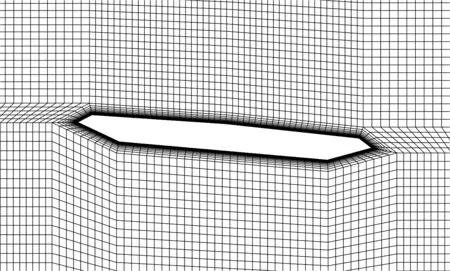
(b) 边界层网格

2.5 理想平板气动特性参数对比验证

理想平板气动外形特殊，在理想流体中的三分力系数和颤振导数均存在理论值.三分力系数的计算公式为[15]

CL=2πα

(6)

CD=0

(7)

(8)

参考文献[16]中的理论公式，可以得到强迫振动理想平板所受的气动自激力，进而得到气动颤振导数的8个理论值.

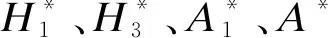
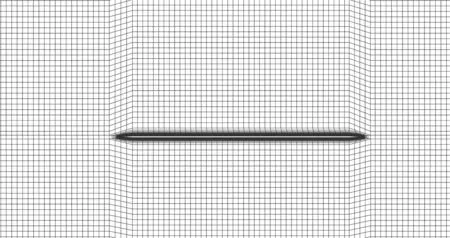
图7 平板边界层网格

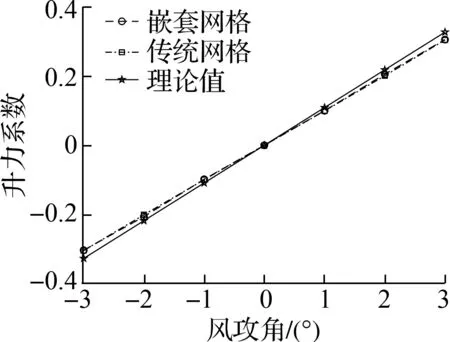
(a) 升力系数

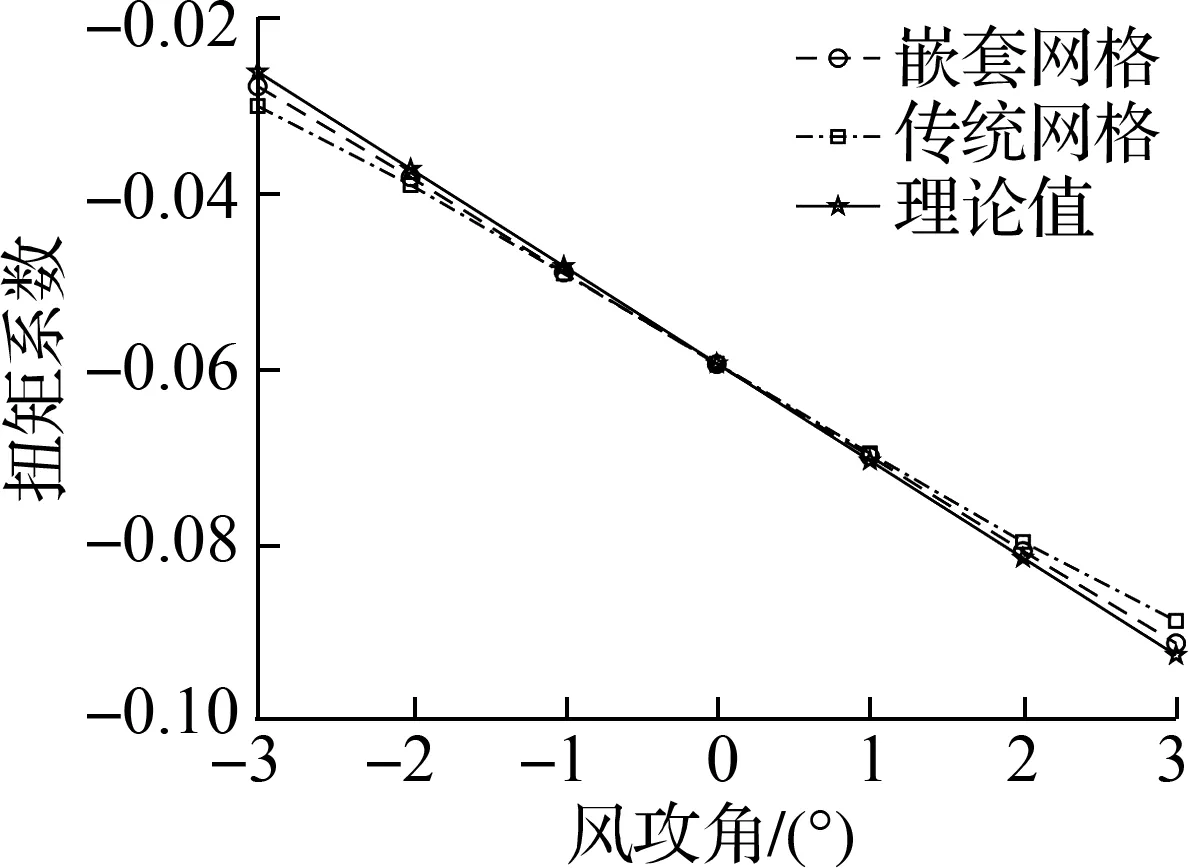
(b) 扭矩系数

3 主梁断面气动特性分析

3.1 静力三分力系数

在数值模拟试验中，为观察不同风攻角工况下流域中流体漩涡的产生、分离、脱落以及风速和风压等流场的基本分布特征，获得大跨度悬索桥主梁二维断面静力三分力系数随风攻角的变化规律，综合考虑了风攻角范围为-6°～6°、风攻角增量Δθ=1°时的13个风攻角，并将其作为基本工况.选取入流风速为10 m/s，时间步为5 ms，计算步为1 000步，共5 s.

将三分力时程监视结果进行无量纲化处理，可得到该大跨度悬索桥主梁断面的三分力系数.

3.2 颤振导数

颤振导数可通过结构强迫振动进行识别.计算时将模型按下式分别作竖向强迫简谐运动和扭转强迫简谐运动：

h(t)=Ahsin(2πft)h(t)=Ahsin(2πft)

(9)

α(t)=Aαsin(2πft)α(t)=Aαsin(2πft)

(10)

竖向简谐运动振幅Ah=10 mm，扭转简谐运动振幅Aα=3°.入口处来流风速设为15 m/s，折算风速VR=2，4，6，8，10，计算时保持来流风速及雷诺数不变.为保证风场发展稳定收敛，时间步长设为1 ms.计算中采用嵌套网格的方法，将桥梁断面模型及模型周围一定区域内的网格作为整体，进行竖向或扭转刚体运动，外围设定为静止网格.

待气动力时程曲线稳定后，选取若干完整周期的气动力曲线样本，采用最小二乘法进行拟合，即可得到大跨度悬索桥主梁断面的8个气动导数.

3.3 2种方法结果对比

分别采用嵌套网格方法和传统网格方法时，悬索桥主梁断面颤振导数结果对比见图10.由图可知，跨度悬索桥主梁采用的扁平钢箱梁断面的数值

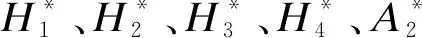
悬索桥主梁断面三分力系数计算结果对比见图11.由图可知，对于大跨度悬索桥扁平钢箱梁断面的静力三分力系数，随着风攻角的增加，主梁的阻力系数呈现先减后增的趋势.流线型扁平钢箱梁并非上下对称，故主梁断面的升力系数不是在风攻角0°时到达零点，而是在2°左右趋于零.扭矩系数随着风攻角的增大而近似线性增大.

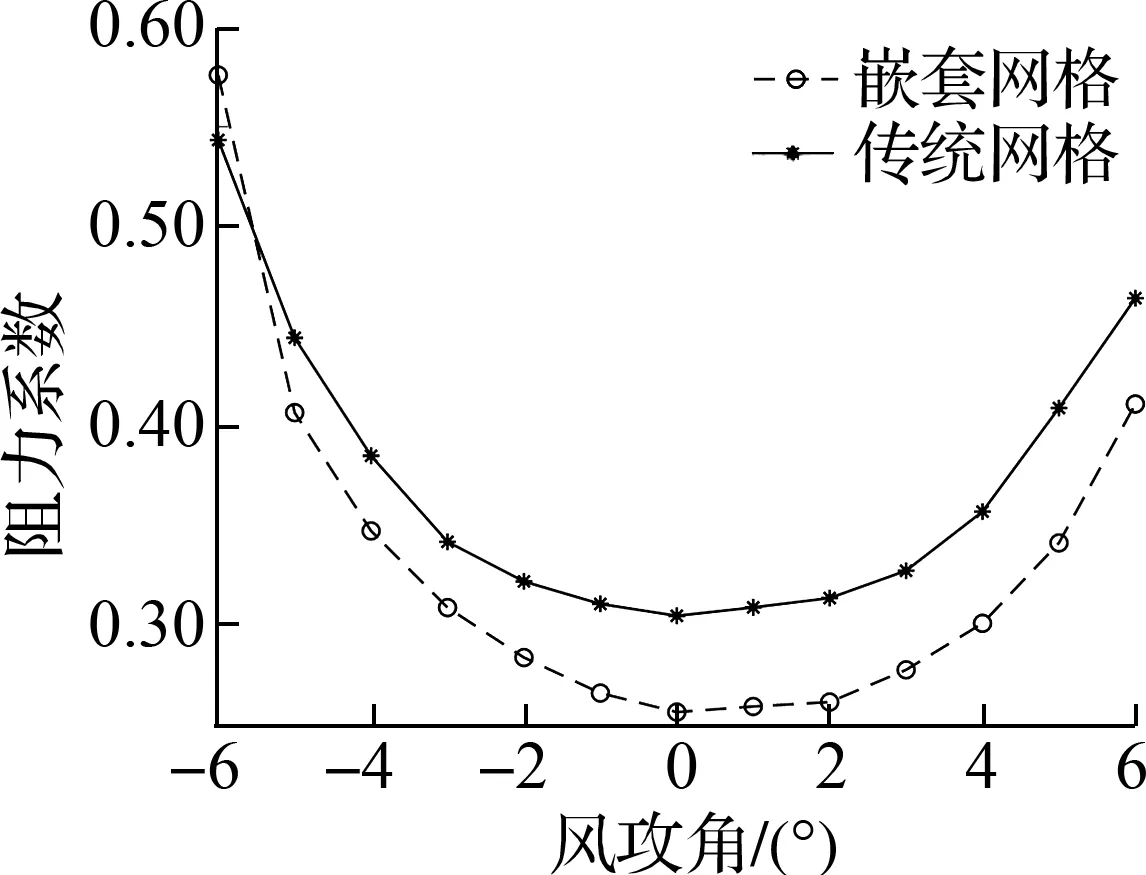
(a) 阻力系数

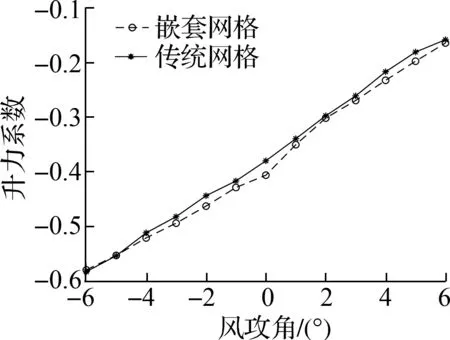
(b) 升力系数

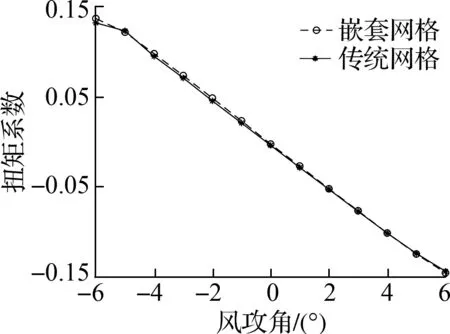
(c) 扭矩系数

图12给出了风攻角为3°时的速度云图.由图可知，传统网格方法和嵌套网格方法识别得到的结果相差较小，流场分布也趋于一致.然而，嵌套网格技术在面对不同风攻角工况时，可以仅旋转组分网格以达到工程需求，从而显著减少网格划分的工作量，提高了工作效率.

(a) 嵌套网格

(b) 传统网格

4 结论

1) 基于CFD技术可有效识别某大跨悬索桥扁平钢箱梁断面的静力三分力系数和颤振导数.模拟过程采用传统网格与嵌套网格.结果表明，两者计算结果接近.三分力系数差异小，扭矩系数几乎重合；颤振导数差异在低折算风速时较小，随折算风速增加而增大，但总体接近.此外，嵌套网格划分简便，工作量较小.