轴向冲击荷载下中空夹层钢管混凝土的动态力学性能分析
宗周红 李佳奇 任逸文 李明鸿 甘 露
(东南大学爆炸安全防护教育部工程研究中心, 南京 211189)(东南大学土木工程学院, 南京 211189)
中空夹层钢管混凝土(concrete-filled double- skin steel tube, CFDST)是一种将部分核心混凝土用空芯钢管取代的新型组合结构.相较于普通钢管混凝土(CFST),CFDST具有自重轻、抗弯刚度大、抗火、抗震和抗爆性能好等优点,是一种具有抵御多灾害作用的优良结构形式,常用于高耸塔桅结构、桥梁结构、高层及超高层建筑等领域[1-4].与其他轴向受力构件类似,中空夹层钢管混凝土柱在其服役期内可能遭受冲击、爆炸和结构倒塌等偶然荷载作用.这些荷载具有低持时、高强度等特点,一旦发生则极易引起严重的经济损失和人员伤亡.因此,深入研究中空夹层钢管混凝土的动力特性和失效机理具有重要的工程应用价值[3-5].
目前,中空夹层钢管混凝土动态力学性能研究主要集中在侧向撞击[6-8]和爆炸防护[3-4,9-10]领域,尚无轴向冲击作用下构件的动力性能研究.在侧向冲击研究方面,Wang等[6]利用落锤对25根圆中空夹层钢管混凝土进行了侧向撞击试验,发现相同冲击能量下,CFDST试件的耐撞性能要优于实心钢管混凝土.基于试验结果,Wang等[7]通过有限元软件ABAQUS对该类构件撞击全过程及影响参数进行了系统性分析,结果表明当空心率大于0.7时,中空夹层钢管混凝土抗撞性能将大幅降低.Aghdamy等[8]通过试验和有限元方法对不同结构参数影响下的构件耐撞性能进行了分析,发现外钢管径厚比、试件长细比和空心率对侧向冲击下CFDST柱动力响应影响最大.在抗爆性能方面,Li等[3-4]对近爆和接触爆炸作用下中空夹层钢管混凝土动力性能进行了研究,结果表明夹层混凝土塑性损伤是该类构件承受爆炸荷载的主要耗能机制.Zhang等[9-10]分析了圆形和方形中空夹层钢管混凝土柱近距离爆炸试验结果,发现当空心率小于0.5时,CFDST与CFST抗爆性能相近.
本文采用试验、数值模拟和理论分析等手段对中空夹层钢管混凝土动态压缩性能进行了研究,分析了空心率、核心混凝土强度、外钢管强度和厚度等参数对试件抗轴向冲击力学性能的影响,探索了中空夹层钢管混凝土的动态应力-应变关系模型,为工程实践提供依据.
1 SHPB试验
本文进行了不同冲击速度下中空夹层钢管混凝土试件的霍普金森压杆(SHPB)冲击试验.4个试件均采用屈服强度fy= 350.0 MPa的无缝钢管和抗压强度fcu=46.5 MPa的混凝土进行制作.试件长度为75 mm, 内、外钢管直径分别为35和70 mm;内、外钢管厚度均为2 mm.
(1)
(2)
(3)
式中,E和A分别为杆件的弹性模量和横截面积;εR、εT分别为反射和透射应变信号;c0为杆件中应力波的传播速度;A0和l0分别为试件的初始截面积和初始长度;t为应变信号对应的时间.

图1 SHPB试验装置
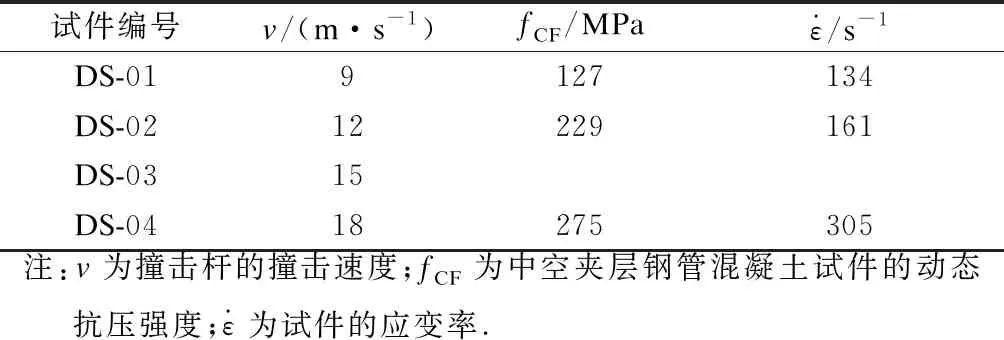
表1 中空夹层钢管混凝土试件参数及试验结果
1.1 冲击破坏现象
图2为典型中空夹层钢管混凝土(试件DS-02)在轴向冲击下的破坏模式.顶面和底面分别指试件靠近入射杆和透射杆的端面.由图可知,轴向冲击荷载下中空夹层钢管混凝土试件保持了良好的完整性.顶面核心混凝土在轴向冲击下产生部分裂缝,但未发生混凝土剥落,底面混凝土裂缝较少,内外钢管产生部分变形.

(a) 顶面

(b) 底面
1.2 应力-应变曲线
图3给出了试件在不同冲击速度(9~18 m/s)下的应力-应变曲线.由图可知,当轴向冲击速度由9 m/s增加到12 m/s时,中空夹层钢管混凝土的动态抗压强度提高了80%;当冲击速度由12 m/s继续增大到18 m/s时,试件动态抗压强度提高了20%.可见,中空夹层钢管混凝土的动态抗压强度随冲击速度的增加而增大,但增长幅度逐渐减小,这与文献[11]中的结论一致.究其原因在于,应变率越高,钢材[12-13]和混凝土[12,14]的应变率强化效应越弱,同时钢管的约束效应也进一步限制了混凝土的应变率强化效应和惯性效应[15-16].
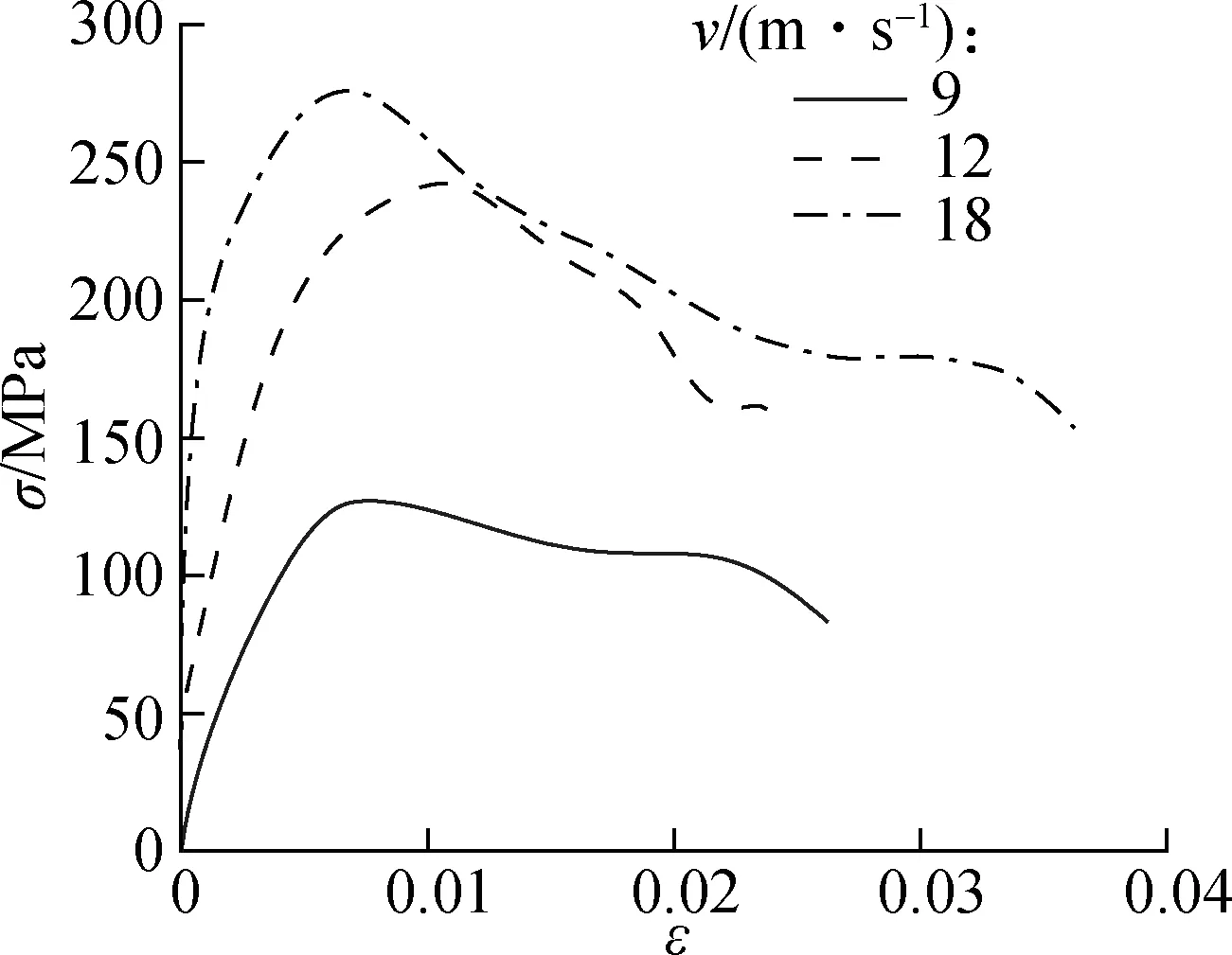
图3 不同冲击速度下试件的应力-应变曲线
1.3 钢管应变时程
中空夹层钢管混凝土在不同冲击速度下的外钢管应变时程曲线见图4.由图可知,加载阶段的钢管轴向和环向应变都近似线性增长,说明本文试验符合恒应变率加载条件[17].当冲击速度为9、12、18 m/s时,钢管最大应变分别为2.015×10-3、5.770×10-3和20.143×10-3.卸载后的钢管仍具有较大的残余应变,说明轴向冲击后外钢管已进入屈服状态,钢管屈服程度随冲击速度增加而不断增加.
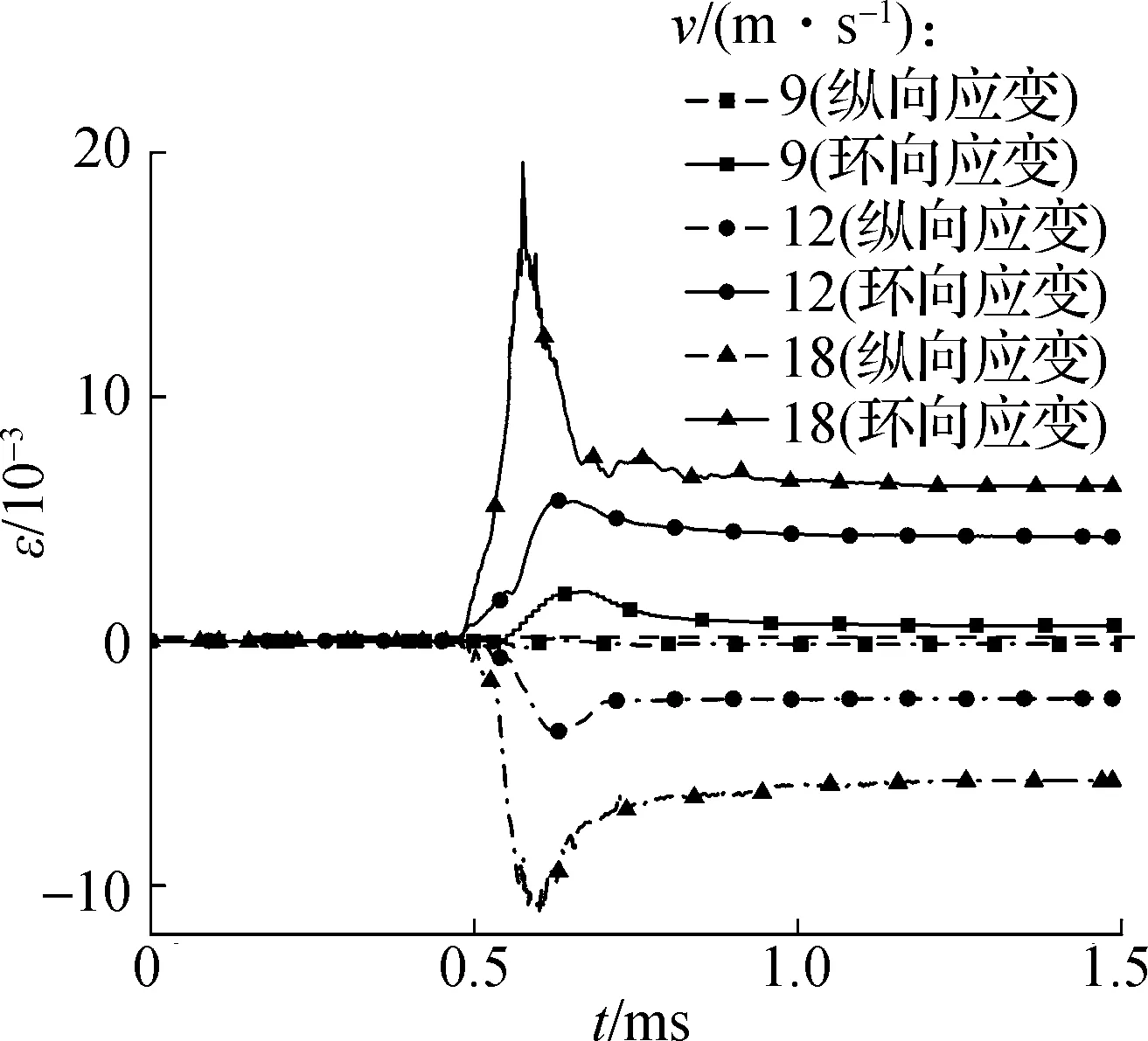
图4 不同冲击速度下的外钢管应变时程曲线
2 冲击响应数值模拟
2.1 数值模型的建立
基于LS-DYNA软件平台,进行轴向冲击试验数值模拟.SHPB试验全模型见图5,分为试件、撞击杆、波形整形器、入射杆与透射杆5个部分,各部分均采用SOLID164三维实体单元进行建模.中空夹层钢管混凝土试件的混凝土本构采用K& C模型,内外钢管本构采用塑性随动强化模型(*MAT_PLASTIC _KINEMATIC),材料强度取2.1节中的实测值;钢压杆采用弹性模型*MAT_ELASTIC,压杆的弹性模量和密度分别为195 GPa和7 850 kg/m3.撞击杆与入射杆间采用自动面面接触;试件端面与入射杆、透射杆之间均采用侵蚀面面接触,内、外钢管与核心混凝土间的接触设置为考虑摩擦效应的面面接触,其中静、动态摩擦系数分别取为0.6和0.5[18].
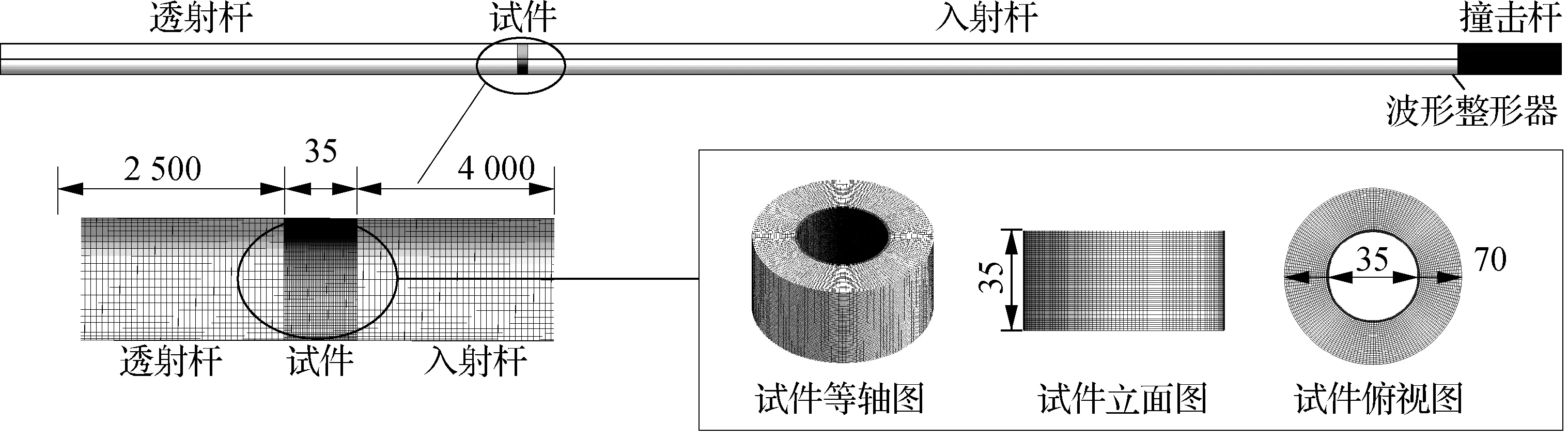
图5 SHPB试验数值模型(单位:mm)
2.2 数值模型的验证
2.2.1 破坏现象对比
中空夹层钢管混凝土典型试件DS-02的数值模拟结果与试验破坏现象对比见图6.由图可知,数值模拟的破坏现象与试验结果相符.在轴向冲击荷载下,试件中混凝土的损伤程度并不均匀.靠近钢管的混凝土由于约束较大,损伤系数也相对较大,远离钢管的混凝土区域材料损伤系数较小.

(a) 试验结果
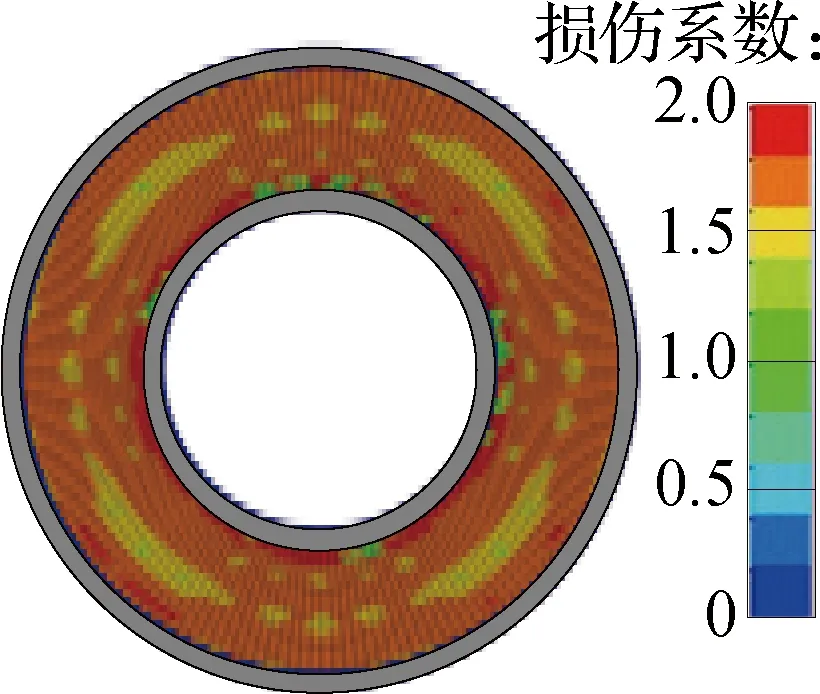
(b) 模拟结果
2.2.2 应力-应变曲线对比
试件实测应力-应变曲线与数值模拟结果对比见图7.由图可知,数值模拟基本能够反映试验中应力-应变曲线的发展规律.然而,受SHPB试验结果的离散性影响,以及有限元模型未能考虑混凝土初始微裂缝与孔洞等原因,数值模拟结果与试验结果仍存在一定差距.

(a) DS-01试件
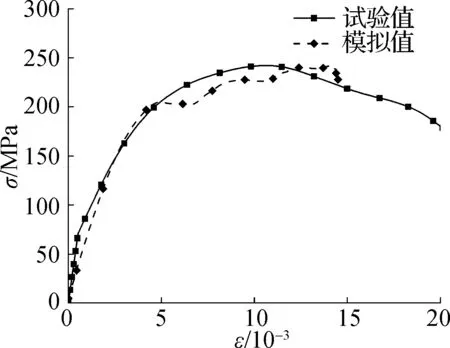
(b) 试件DS-02
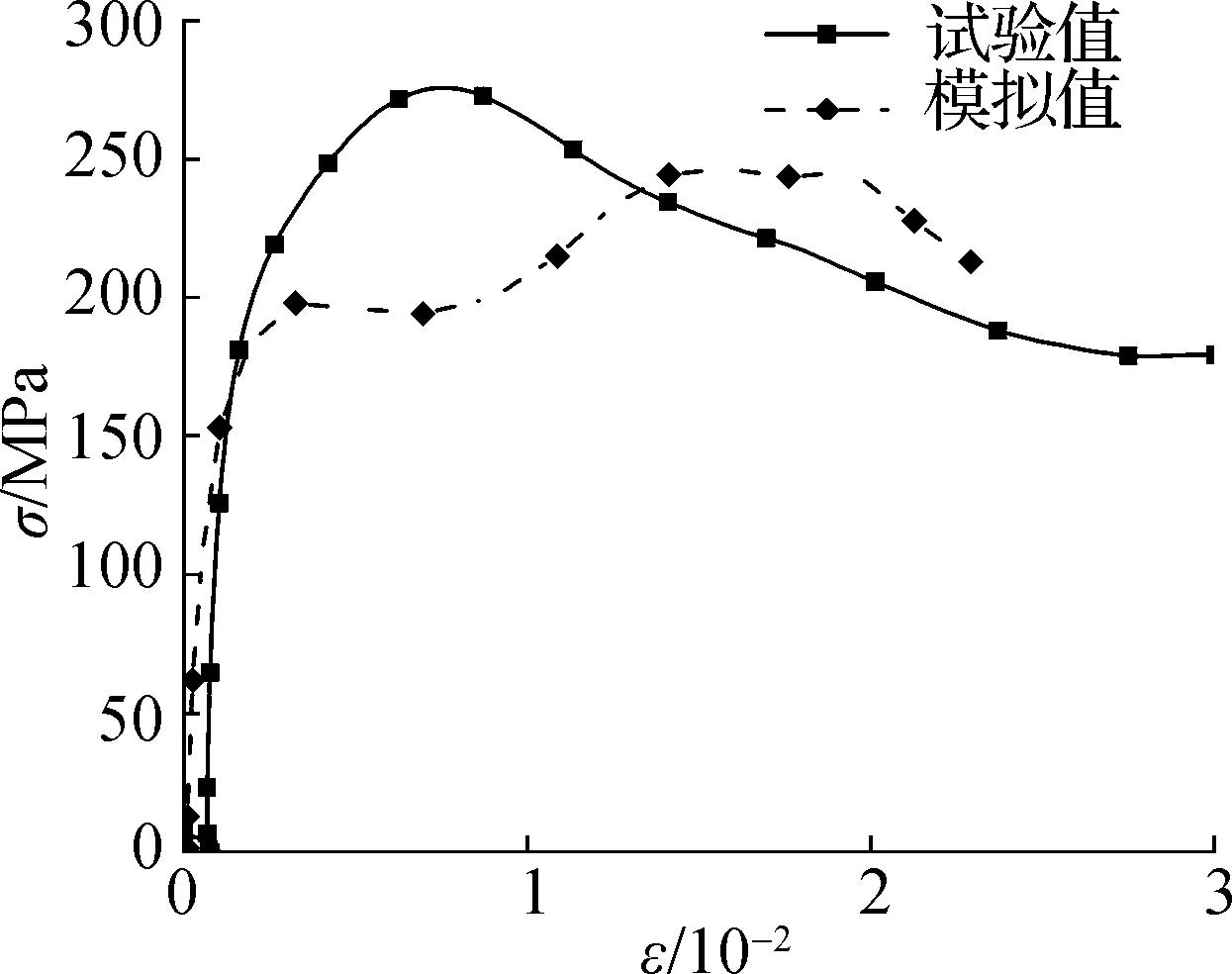
(c) 试件DS-04
2.3 受力机理
图8给出了中空夹层钢管混凝土试件DS-02在轴向冲击荷载下各部分的内力分配变化.图中,k为各部分承载力与全截面承载力之比.轴向冲击前期(t=0~0.25 ms),核心混凝土和外钢管为中空夹层钢管混凝土的主要承载部分,对全截面承载力的贡献比均为39%,内钢管的贡献比为22%.进入轴向加载后期(t>0.25 ms),核心混凝土承载力对全截面承载力贡献比不断增大,内外钢管对承载力的贡献比不断减小.
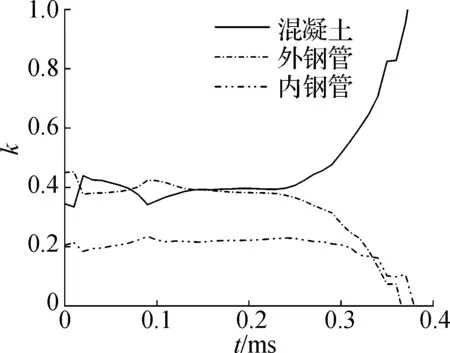
图8 各部件内力分配
轴向冲击过程中,内外钢管对核心混凝土约束应力p的时程曲线见图9.由图可知,轴向冲击初期(t=0~0.25 ms),由于混凝土侧向膨胀大于钢管,内外钢管对混凝土约束作用近似线性增加.冲击过程结束后(t>0.4 ms),试件各部分产生塑性变形,内外钢管对混凝土的约束应力稳定在一定范围内.对比内外钢管对混凝土约束应力时程曲线可以发现,外钢管对混凝土的约束作用大于内钢管约束作用,且外钢管对混凝土的约束应力发展进程滞后于内钢管.
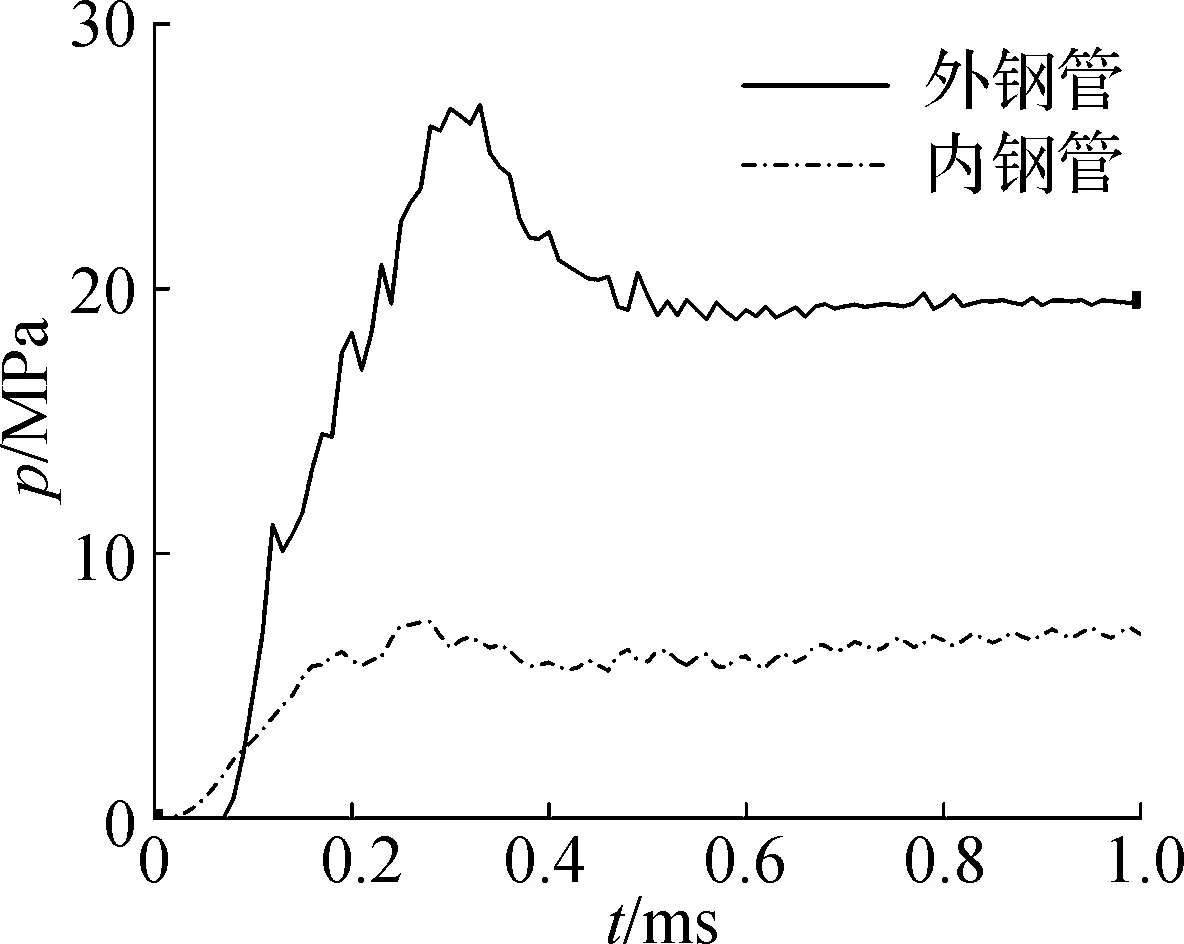
图9 钢管对混凝土约束应力时程曲线
2.4 参数影响分析
在数值模拟分析中,基准试件尺寸同表1,增加参数取值如下:钢管强度fy=235,420 MPa,混凝土强度fcu=30,60 MPa,外钢管厚度do=0.5,1.0,2.5,3.0 mm,空心率χ=0.30,0.75.以控制变量的方式研究这些参数对中空夹层钢管混凝土动力特性的影响.
2.4.1 材料强度
图10给出了中空夹层钢管混凝土动态抗压强度随材料强度的变化规律.由图可知,在相同的冲击速度下,随材料强度的提高,试件的动态抗压强度逐渐增大.以撞击杆的冲击速度14 m/s为例,钢材强度从235 MPa分别增加到350和420 MPa时,试件的动态抗压强度分别增加了10.7%和12.3%;当混凝土强度从30 MPa分别增加到45和60 MPa时,试件动态抗压强度分别增加了3.5%和8.5%.此外,当材料强度相同时,随着冲击速度的增大,试件的动态抗压强度也随之增大,但增加幅度有所减小.
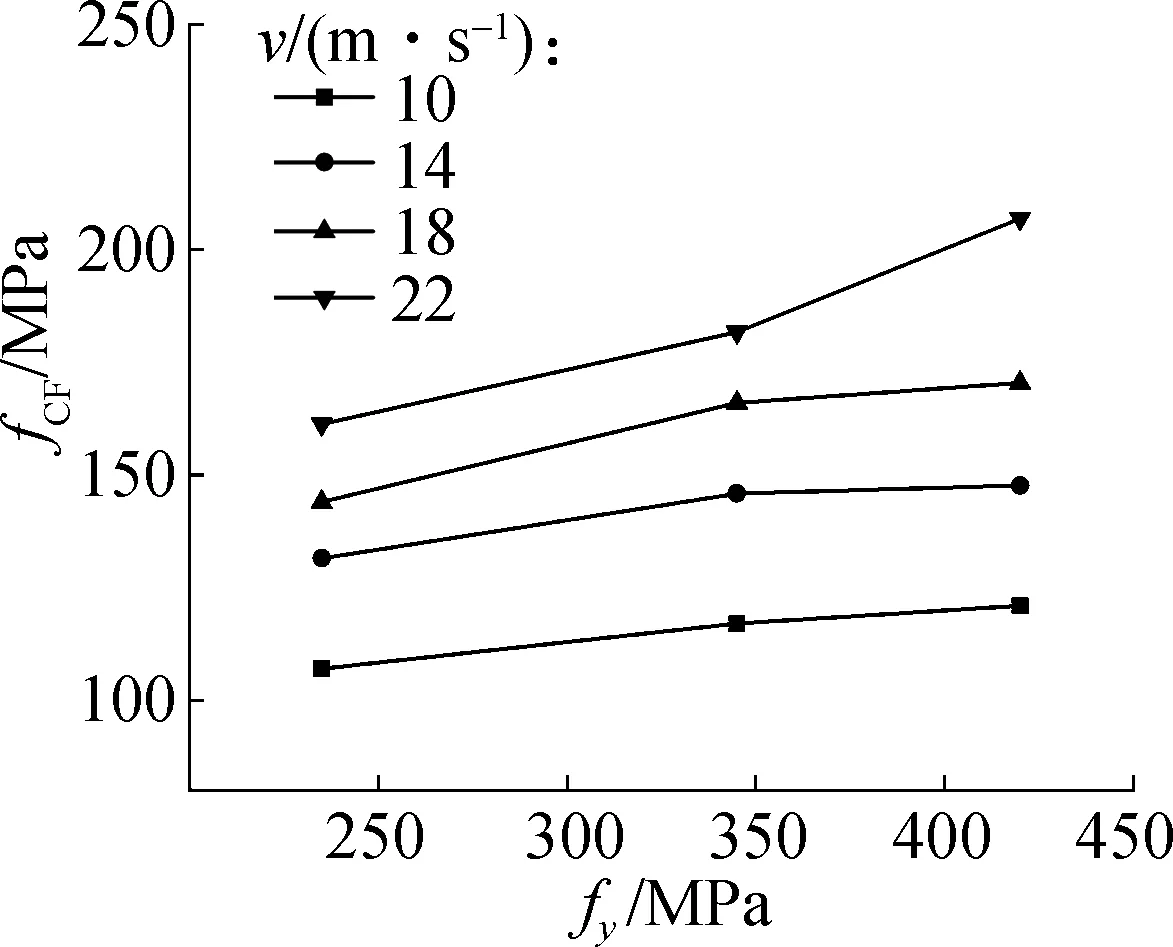
(a) 外钢管强度
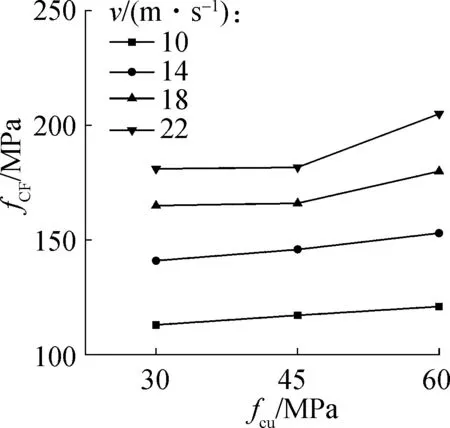
(b) 混凝土强度
2.4.2 外钢管厚度
中空夹层钢管混凝土动态抗压强度随外钢管厚度do的变化规律见图11.在本文研究的参数范围内,随着外钢管厚度的增加,试件的动态抗压强度逐渐增大.以冲击速度22 m/s为例,当外钢管厚度从1 mm增大到2和3 mm时,试件的动态抗压强度分别增长了40.8%和71.0%.这主要是因为外钢管厚度的增加使得外钢管截面面积及对混凝土的约束作用同时增大,进而增强了试件的动态抗压强度.
2.4.3 空心率
图12给出了动态抗压强度随试件空心率χ的变化规律.从图中可以看出,随着空心率的增加,中空夹层钢管混凝土动态抗压强度逐渐降低.以冲击速度22 m/s为例,当试件空心率从0.30增加到0.53和0.75时,动态抗压强度分别下降了32.7%和38.9%.这主要是因为空心率增加时,试件中内钢管截面面积增加,但混凝土面积减小,内钢管提供的强度增加量小于混凝土引起的强度减少量[19].
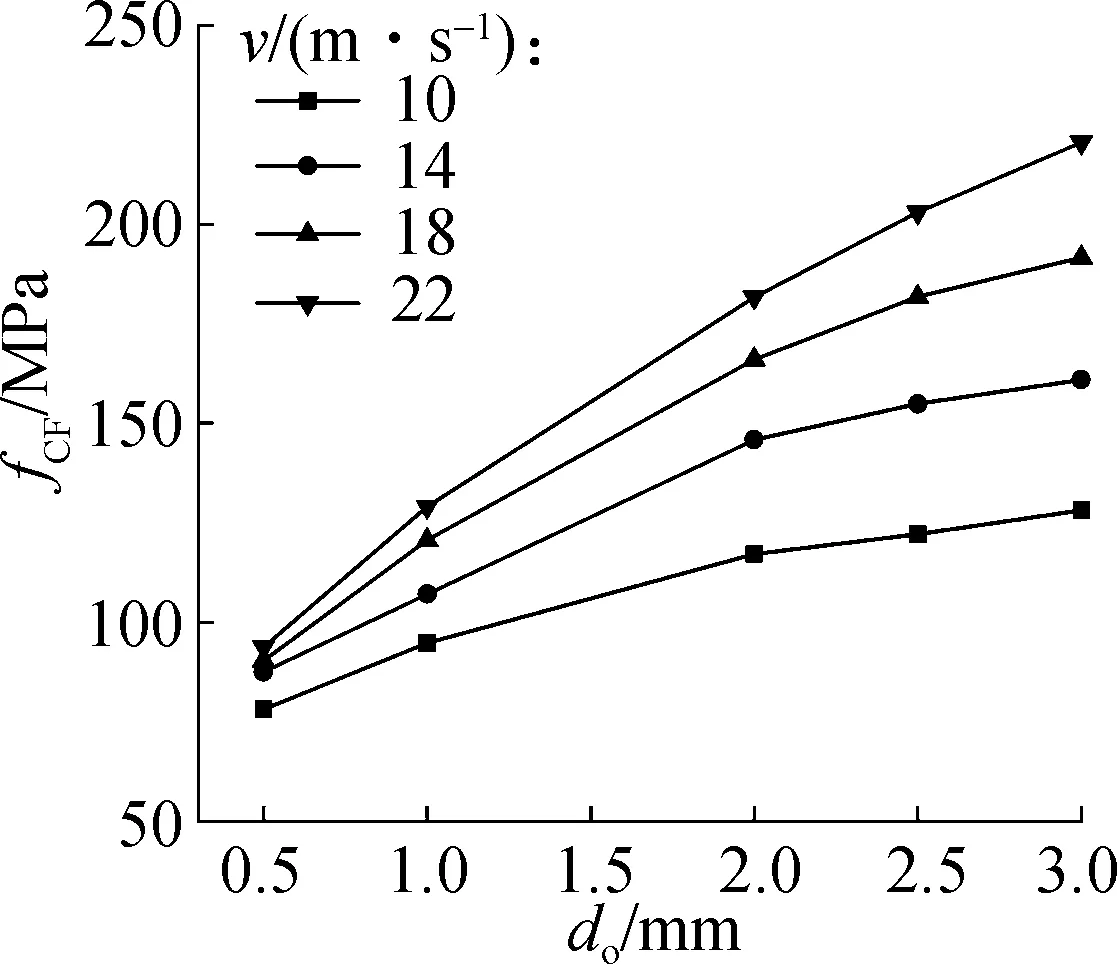
图11 外钢管厚度对动态抗压强度的影响
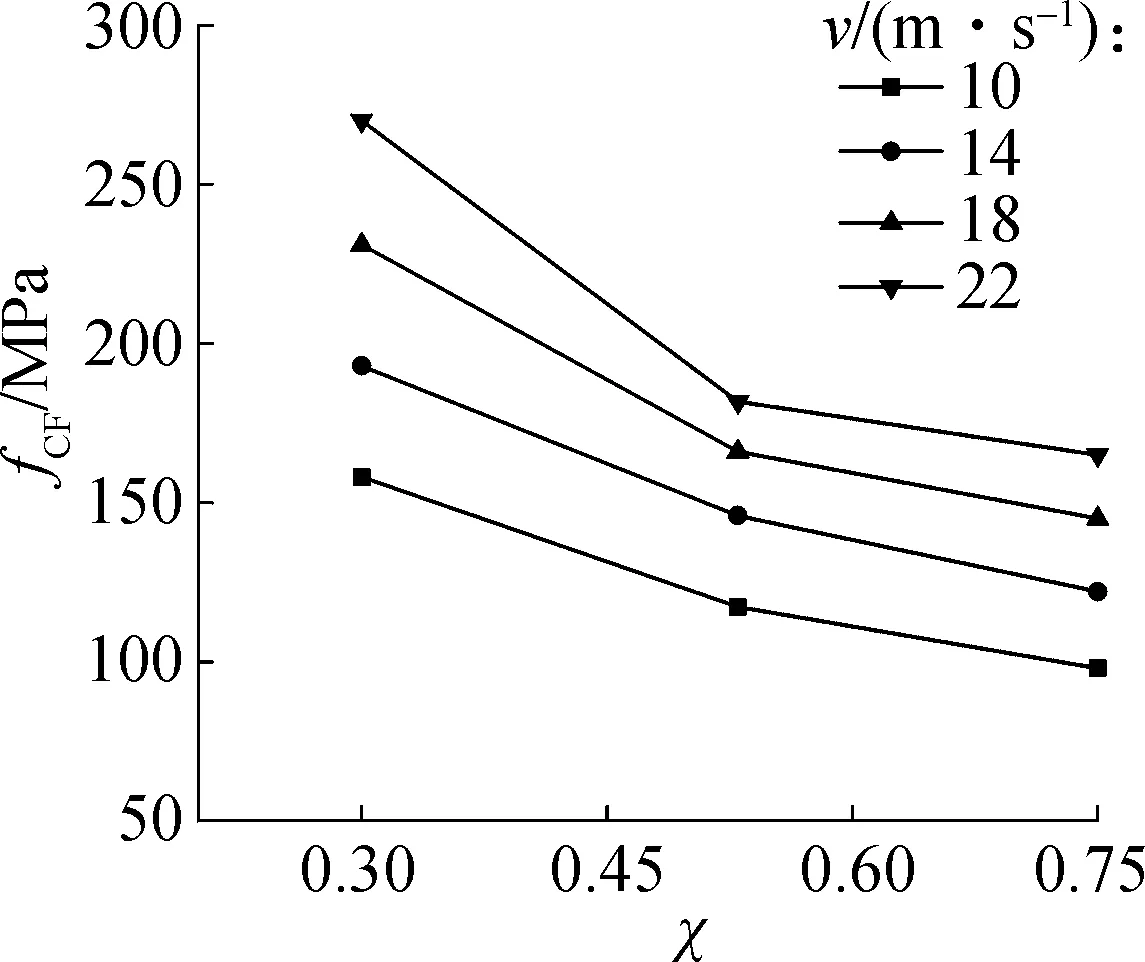
图12 空心率对动态抗压强度的影响
3 动态应力-应变关系
相同外钢管尺寸条件下,中空夹层钢管混凝土较实心钢管混凝土试件中的部分混凝土被内钢管取代,导致钢管与核心混凝土间的约束作用发生变化.本文基于文献[20]建议的钢管混凝土动态应力-应变模型,采用削弱核心混凝土的方式,对动态峰值应力σ0d和对应的峰值应变ε0d进行空心率修正,即
σ0d=σ0k1
(4)
ε0d=ε0k2
(5)
k1=aχb
(6)
k2=cχd
(7)
式中,k1为峰值应力修正系数;k2为峰值应变修正系数;a、b、c、d为待定参数.
确定参数a、b、c、d属于多目标优化问题,实际上是寻找pareto最优解集.本文采用粒子群优化算法(particle swarm optimization, PSO)进行优化求解[21],解得a、b、c、d分别为1.950 9、0.018、2.84、0.411.一次优化后的结果见图13.可以看出,一次优化后的试件应力-应变曲线与试验曲线上升段和极限强度吻合良好,但是下降段差别较大.
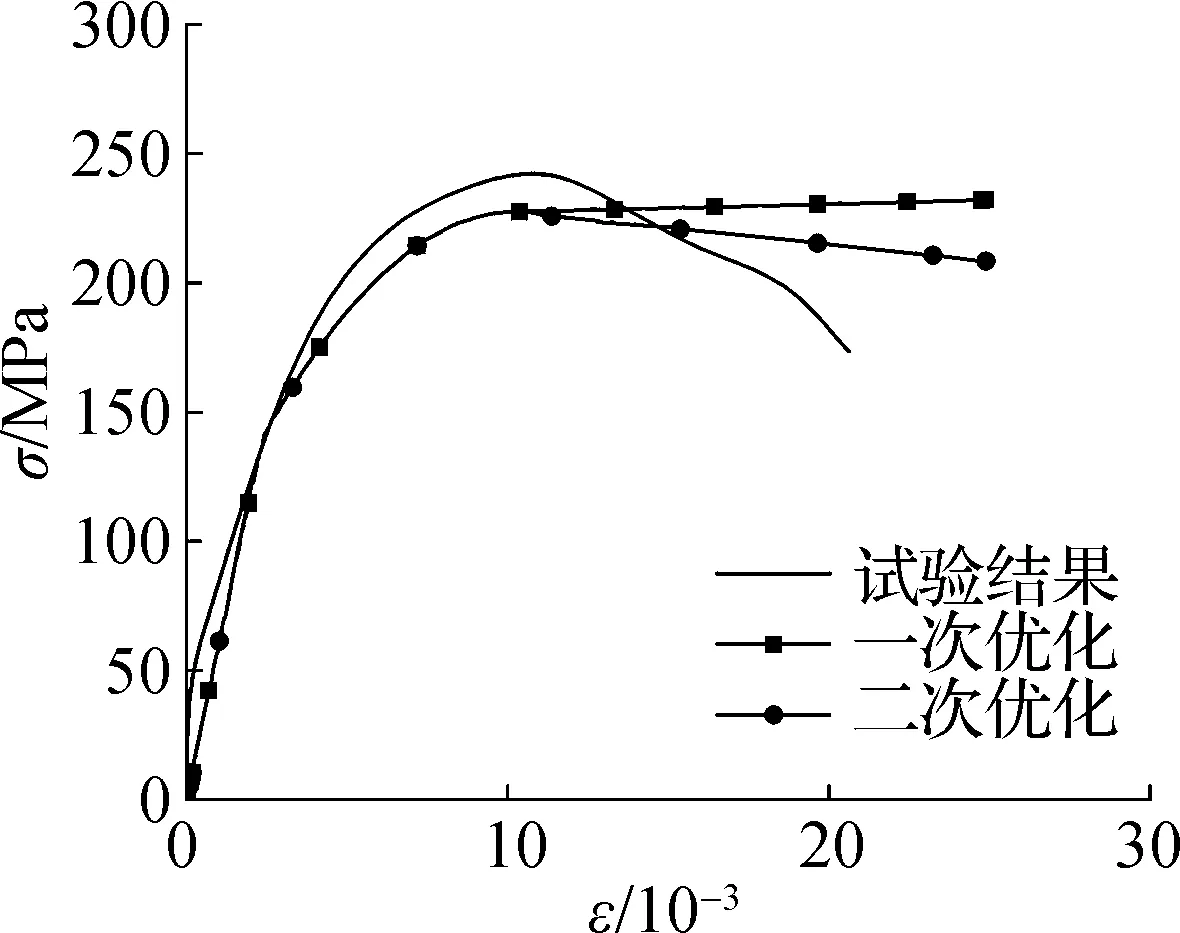
((a) 试件DS-02
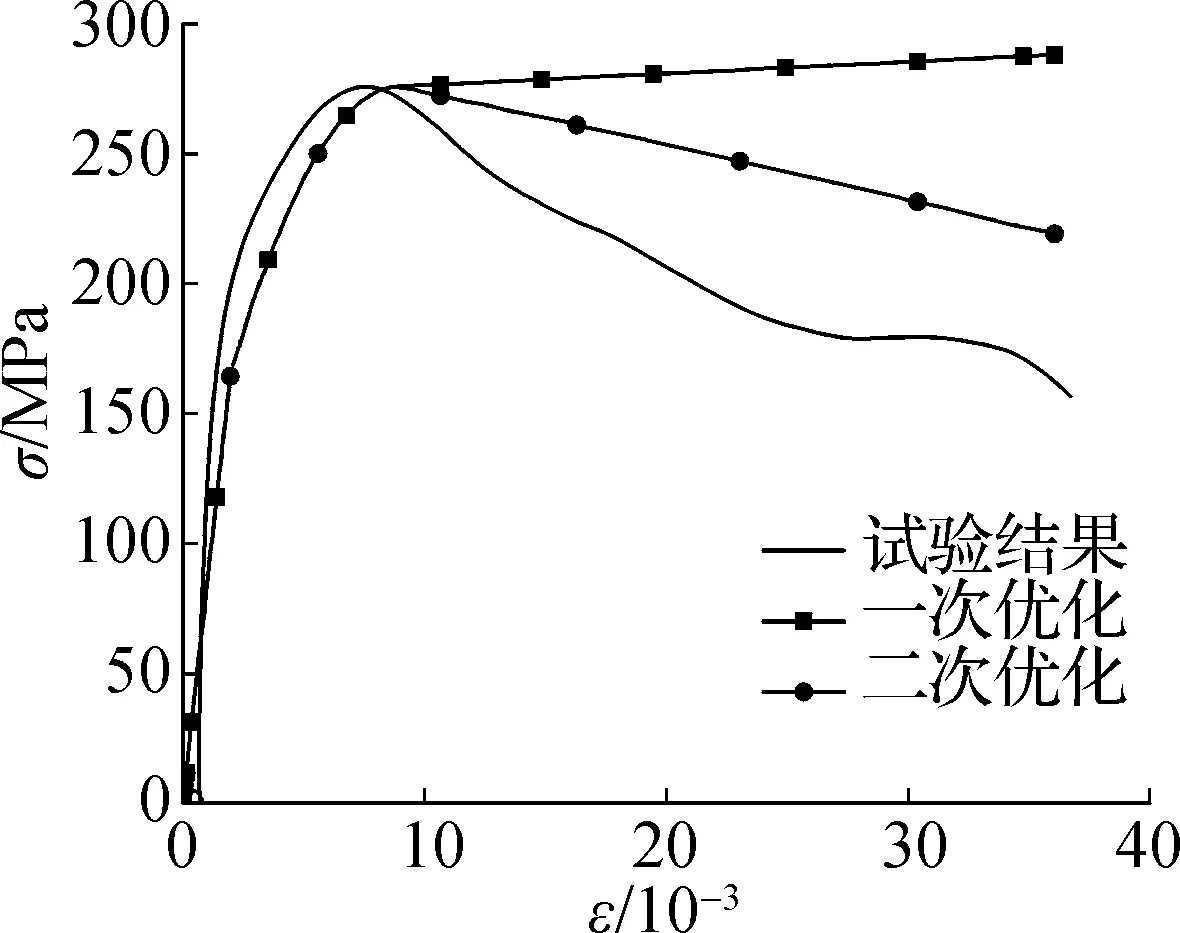
(b) 试件DS-04
考虑到轴向冲击荷载下试件的核心混凝土内部容易产生大量的微裂纹、微空洞以及骨料破裂等问题,需要在原本的应力-应变曲线中引入损伤效应,以表征试件在加载后期的承载力降低现象.本文采用文献[22]中的应变等效假定,对求得的应力进行修正,即
σ=(1-D)σi
(8)
式中,σi为不考虑损伤时的应力;D为损伤程度参数,其计算公式为[23]
(9)
式中,KD为损伤因子;εth为损伤演化中开始计入损伤影响的应变阈值;δ为材料参数,以表征冲击脆化与冲击韧性现象.
修正后的中空夹层钢管混凝土应力-应变曲线见图13.可以看出,二次优化后的理论应力-应变曲线下降段与试验曲线吻合较好,整体能够反应轴向冲击荷载下试件的应力-应变发展情况.
4 结论
1) 轴向冲击荷载作用下,中空夹层钢管混凝土中核心混凝土产生裂纹,外钢管进入屈服阶段,但试件完整性较好.
2) 中空夹层钢管混凝土动态抗压强度随撞击速度的增加而增大,但增长幅度逐渐减小.
3) 建立的中空夹层钢管混凝土SHPB数值模型能够较好地模拟实际冲击加载过程.数值分析表明:轴向冲击下,靠近钢管的混凝土区域损伤较为严重;混凝土和外钢管是试件的主要承载部分;外钢管对混凝土约束作用大于内钢管,但外钢管对混凝土约束作用进程滞后于内钢管.
4) 对验证后的数值模型进行参数分析.结果表明:相同冲击速度下,材料强度的提高、外钢管厚度的增大或空心率的减小,都能使中空夹层钢管混凝土试件的动态抗压强度增大.
5) 基于实心钢管混凝土应力-应变关系模型和多目标粒子群优化算法,建立了中空夹层钢管混凝土的动态应力-应变关系模型,可供工程抗冲击设计及分析参考.

