空爆载荷作用下固支弹塑性圆板的动力学模型
吴 迪,米 国,郭香华,张庆明
(北京理工大学机电学院, 北京 100081)
在结构的动力响应中,通常既有弹性变形,又有塑性变形,并且两种变形场的分界面随时间不断发生变化,因此,在求解弹塑性动力响应时,不仅需要对不同区域采用不同的本构关系,还要处理复杂的动边界问题。现有的关于结构在强动载荷下响应的理论研究[1-3]大多把材料假定为理想刚塑性,同时忽略材料的应变强化效应和应变率效应,从而简化理论分析过程。Duffey[4]通过构建板的初始动能等于塑性变形耗散能的能量守恒方程来计算固支圆板在爆炸载荷下的最终挠度,这种方法假定板的位移分布始终满足形函数,并且径向位移的影响可以忽略。然而这一假设仅在小挠度情况下是合理的,当板的中心点挠度与板的厚度为同量级甚至存在几十倍差异时,膜力效应将逐渐显著,甚至超过弯矩效应而在抵抗板的变形中起主导作用。
Nurick 等[5]指出,忽略径向位移对估算平板挠度的影响不大,但会导致计算的膜应变分布与试验获得的应变分布相反,即中心小、外围大,为此提出了一个考虑径向位移的理论模型,得到了与试验结果吻合的膜应变分布。Jones[6]提出了一种同时考虑弯矩和膜力的理论方法,用以描述在弯矩和膜力都很重要的挠度范围内刚塑性圆板的力学行为,比较准确地预测了Florence[7]记录的简支圆板在均匀载荷作用下的最终变形。然而这种近似理论分析虽然同时考虑了板的膜效应和弯曲效应,但没有考虑它们的联合效应,即弯曲效应和膜效应是解耦的。Cloete 等[8]考虑径向位移并将弯曲应变和膜应变耦合处理,提出了刚塑性薄圆板在冲击载荷下的解析解,但没有考虑结构的弹性响应。
近年来,研究人员开始将研究重点转移到薄板大挠度变形的弹性效应上。Campbell 等[9]研究了集中力作用下固支梁响应的理论模型,将梁的响应分为3 个阶段,即弹性阶段、弹塑性阶段和塑性阶段,并基于力矩平衡构建了梁在不同阶段的载荷-位移关系式,但模型中没有考虑卸载阶段。Karagiozova 等[10]研究了固支圆板在准静态均布载荷下的弹塑性响应,基于能量法得到了圆板在加载和卸载阶段的载荷-位移关系式。
等效单自由度(single degree-of-freedom,SDOF)模型简单实用,输入参数相对较少,在工程中常用于预测结构在爆炸载荷作用下的动力响应。SDOF 模型由Biggs[11]提出,其基本物理量是等效质量、等效刚度和等效抗力等。
战场上装甲车辆防护的根本目标是避免乘员受到致命伤害,因此车辆结构在爆炸载荷作用下的变形不能过大,否则舱内超压及结构碰撞形成的破片都将危及乘员生命。研究钢板在爆炸载荷下的弹塑性响应对于装甲车辆防雷结构设计具有重要意义。本研究针对固支弹塑性圆板在空中近爆载荷作用下的变形,建立其加载和卸载全过程的动力学模型,研究弯矩和膜力联合承载范围内的挠度。钢板承受的载荷并非均匀分布,爆轰产物首先作用于固支圆板的中心,随后扩散并作用于整个圆板表面,因此,圆板中心挠度最大且最先进入塑性阶段,并迅速向板边界扩散。本研究的工况中圆板最终仅发生弹塑性大变形,而未发生破坏。基于文献[12]中的试验工况建立有限元模型,通过有限元数值模拟得到空爆作用下固支圆板的动态响应,对比动力学模型计算结果、试验结果及数值模拟结果,验证动力学模型的有效性,研究结果可以应用于固支圆板在空中近爆载荷作用下的大变形预测。
1 动力学模型推导
1.1 载荷等效
空中近爆作用下,作用在板上的爆炸冲击载荷具有明显的时空分布。可采用能量等效的方法将不均匀载荷转化为等效均匀载荷[13]。近爆作用下结构上的爆炸冲击载荷达到峰值的时间差别很小,因此,可以假设载荷只有空间分布,即圆板上各点载荷随时间变化的函数一致,如图1 所示。

图1 载荷等效示意图Fig. 1 Equivalent load diagram

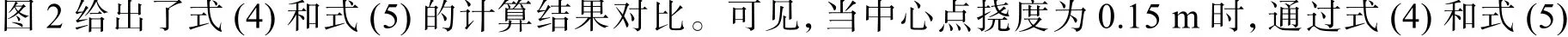

图2 式 (4)和 式 (5)的计算结果对比Fig. 2 Comparison of calculation results between Eq. (4) and Eq. (5)
式中:H为圆板的初始厚度。
1.2 屈服条件
当板挠度的量级超过板厚度时,膜力和弯矩的作用同样重要,板元的受力分析如图3 所示,其中:Nr为径向膜力,Nθ为周向膜力,Mr为径向弯矩,Mθ为周向弯矩。
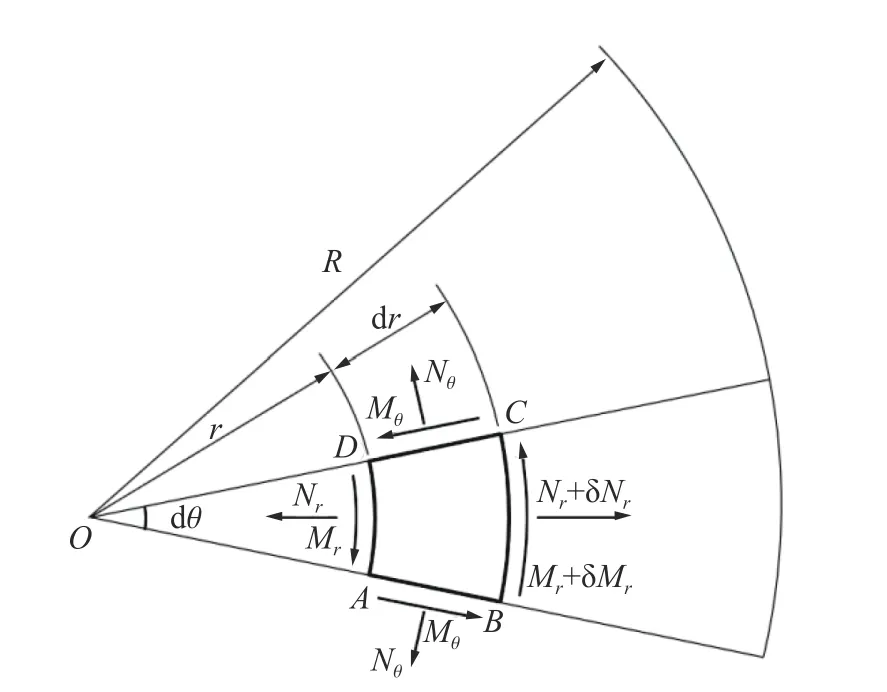
图3 板元受力分析Fig. 3 Force analysis of plate microelement
因此,如图4 所示,采用弯矩和膜力联合承载的屈服条件[15]

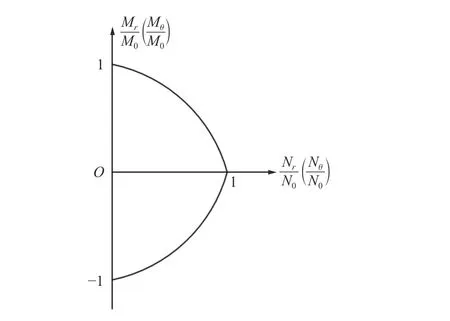
图4 弯矩和膜力联合承载的屈服条件Fig. 4 Yield condition of combined bending moment and membrane force
1.3 加载阶段的应力场和变形能场
固支圆板发生大变形过程中,除了形成较大的横向挠度外,还会发生径向和周向位移,其应变分布为


当固支圆板发生足够大的横向位移时,根据弯矩与膜力之间的不同关系,沿板的半径可以定义3 个区域:弹性区、塑性膜区、弯矩与膜力联合承载的塑性区,如图5 所示。最靠近边界的区域,即RP<r≤R区域,为弹性区。弹性区以外的区域都是塑性区,满足屈服条件,即式 (7) 和式 (8),其中:0≤r≤RPN区域满足N=n0,M= 0,结构进入塑性流动,此时仅膜力参与承载,也就是塑性膜区域;而RPN<r≤RP区域则是弯矩与膜力联合参与承载的塑性区。
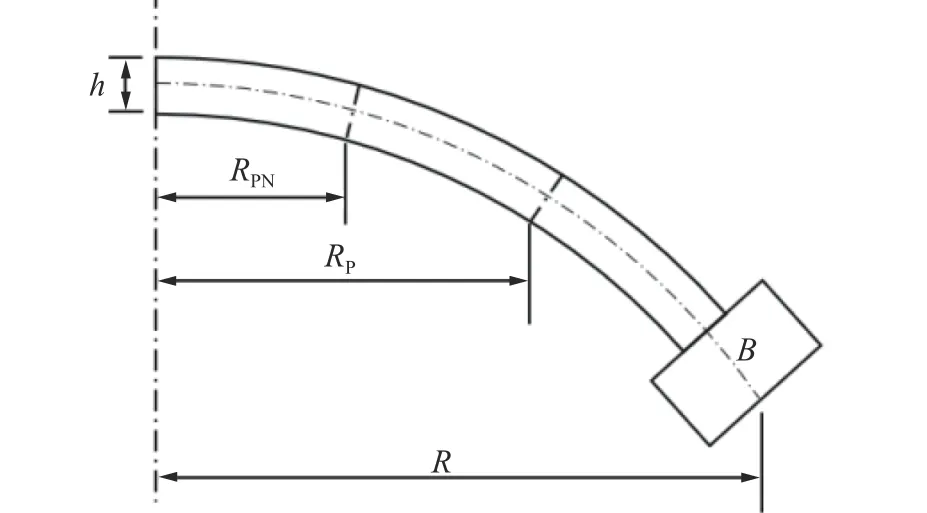
图5 固支圆板发生弹塑性大变形后的应力场分布Fig. 5 Stress field of clamped circular plate after large elastic-plastic deformation
半径RP沿圆板半径r分隔弹性和塑性区域,将式 ( 14) 和式( 15) 代入式( 7)可以求得


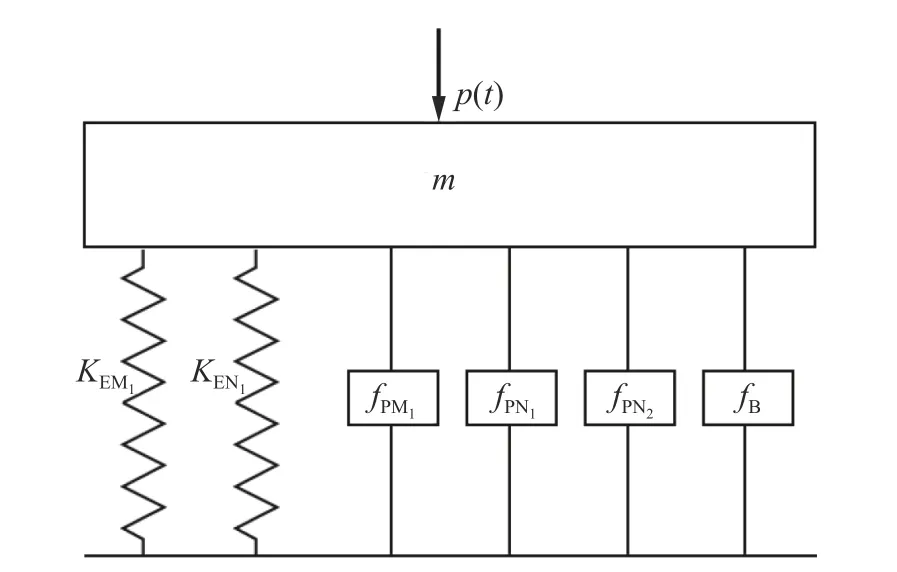
图6 加载阶段的等效质量-弹簧-阻尼模型Fig. 6 Equivalent mass-spring-damper model in loading
1.3.1 弹性区加载


1.4 卸载阶段的应力场和变形能场
在爆炸加载过程中,弹性变形和塑性变形均随外力增大而增大,外力卸载后,弹性变形可以恢复,塑性变形不能恢复,且塑性变形不积累变形能。与弹塑性有限元原理类似,本研究假设弹性变形与塑性变形不耦合,弹性变形积累的弹性势能与塑性变形耗散能互不影响,具有各自独立的分布规律,变形也有各自独立的分布规律,即
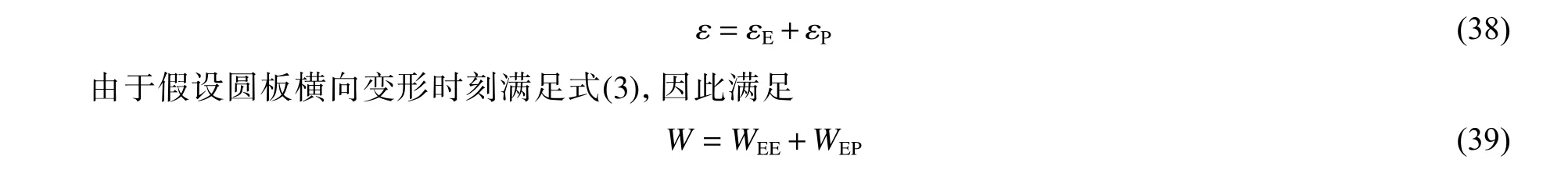
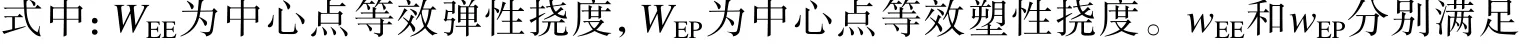

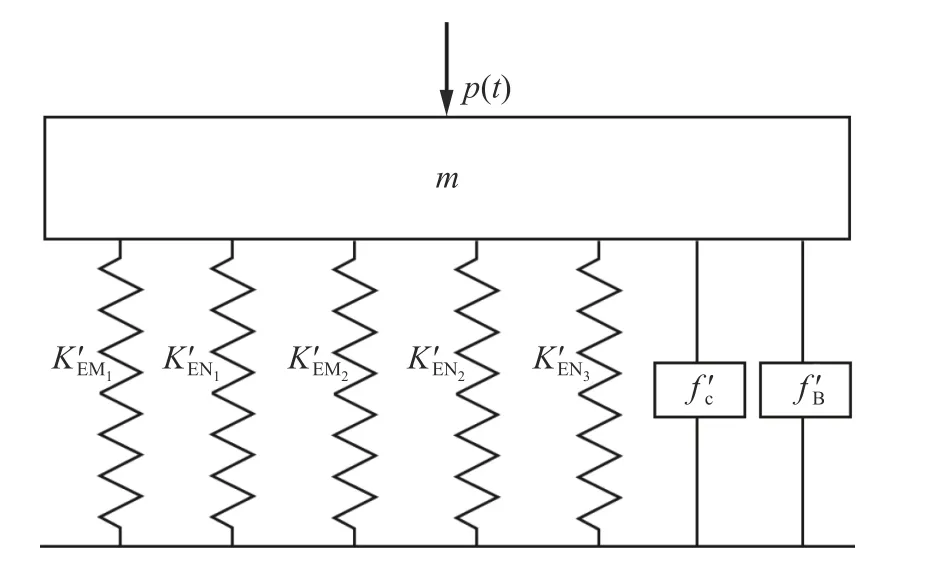
图7 卸载阶段的等效质量-弹簧-阻尼模型Fig. 7 Equivalent mass-spring-damper model in unloading phase

边界处旋转角度

1.5 外力功等效

1.6 质量等效
根据SDOF 模型,动能与圆板动能相等,求解等效质量
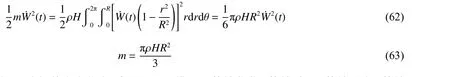
针对变形的不同阶段,分析其应力状态,求出SDOF 模型的等效载荷、等效质量、等效刚度、等效抗力,代入SDOF 模型的运动方程进行求解,通过多个阶段的叠加,可以得到固支弹塑性圆板在空爆作用下的完整动态响应。
2 有限元数值模拟
基于高强度圆形钢板空中近爆试验工况[12],建立有限元模型,进行数值模拟计算,并与试验结果[12]对比,验证有限元模拟结果的有效性。
试验中使用球形TNT 裸装药,从炸药中心点起爆。靶板由上下压板夹紧固支,上压板的厚度为50 mm,下压板的厚度为80 mm,靶板与上下压板的尺寸均为 1 .5 mm×1.5 m,靶板受空爆载荷作用的范围为半径0.5 m 的圆。试验布置见图8。
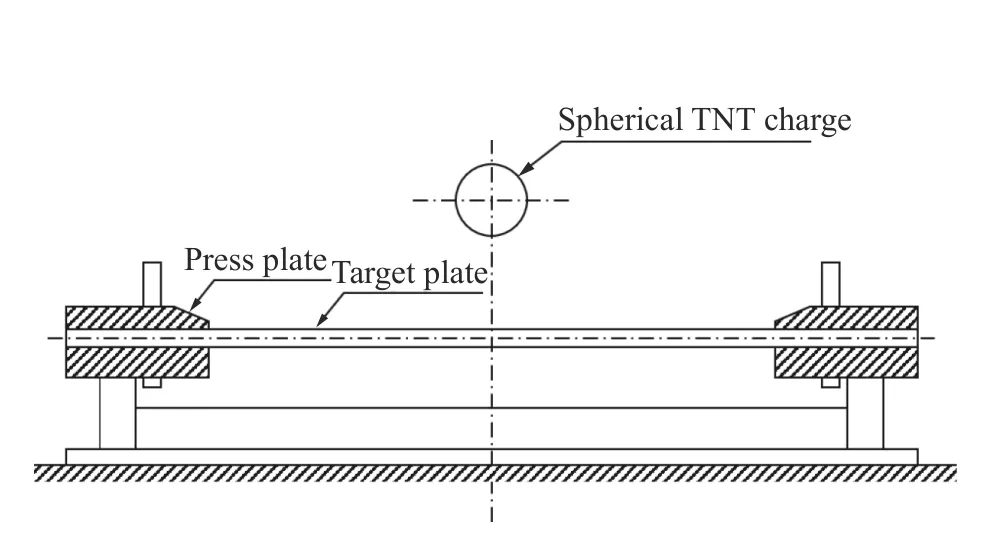
图8 试验布置Fig. 8 Test setup
试验工况如表1 所示。
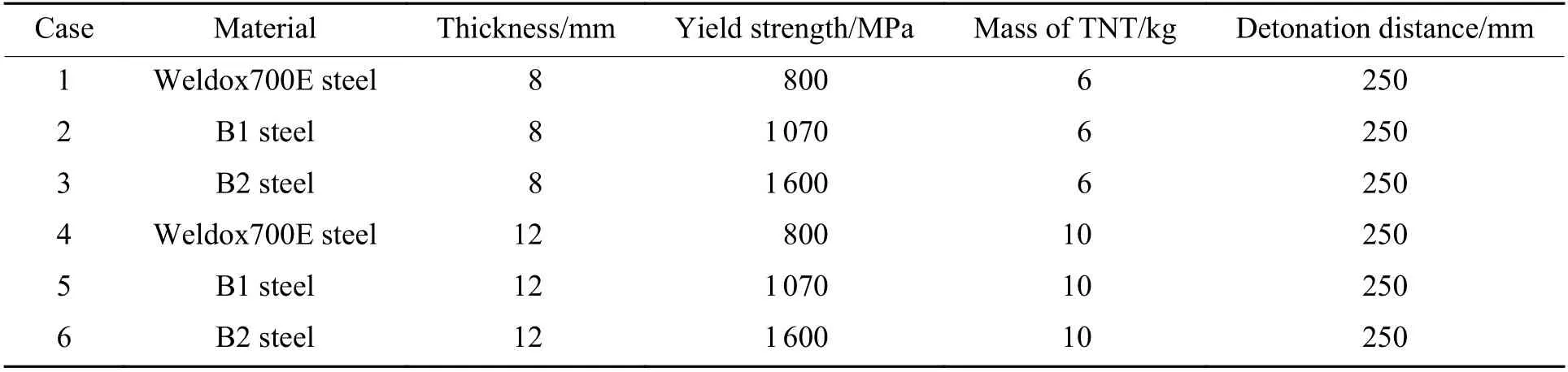
表1 3 种高强度钢的试验参数[12]Table 1 Test parameters of three kinds of high strength steel[12]
按照试验工况,通过显式有限元动力分析软件LS-DYNA 建立有限元模型,对TNT 爆炸冲击波在空气中的传播及其与固支圆板的相互作用进行模拟。空气和上下压板采用六面体网格划分,压板采用刚体材料模型描述,靶板采用二维网格划分,基于任意拉格朗日-欧拉(arbitrary Lagrangian-Eulerian,ALE)算法进行数值模拟分析。图9 为有限元模型示意图。各工况下模拟得到的中心点位移-时间曲线如图10 所示。
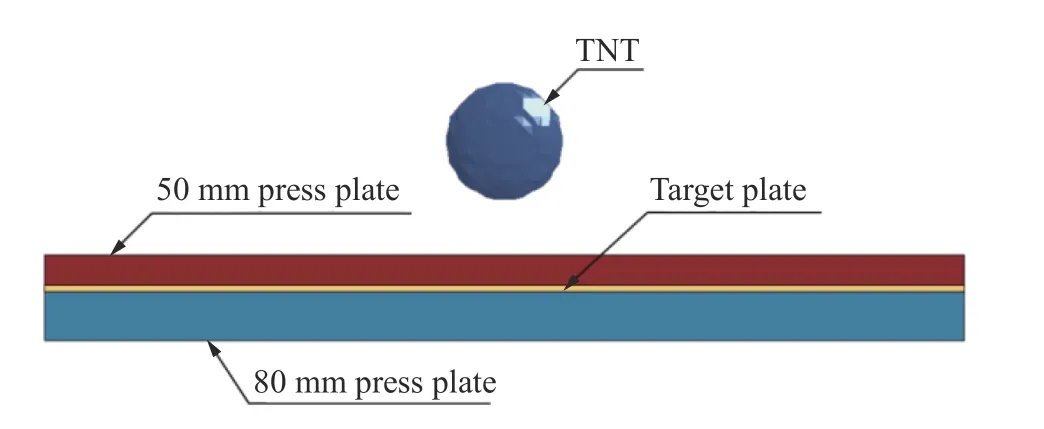
图9 有限元模型Fig. 9 Finite element model
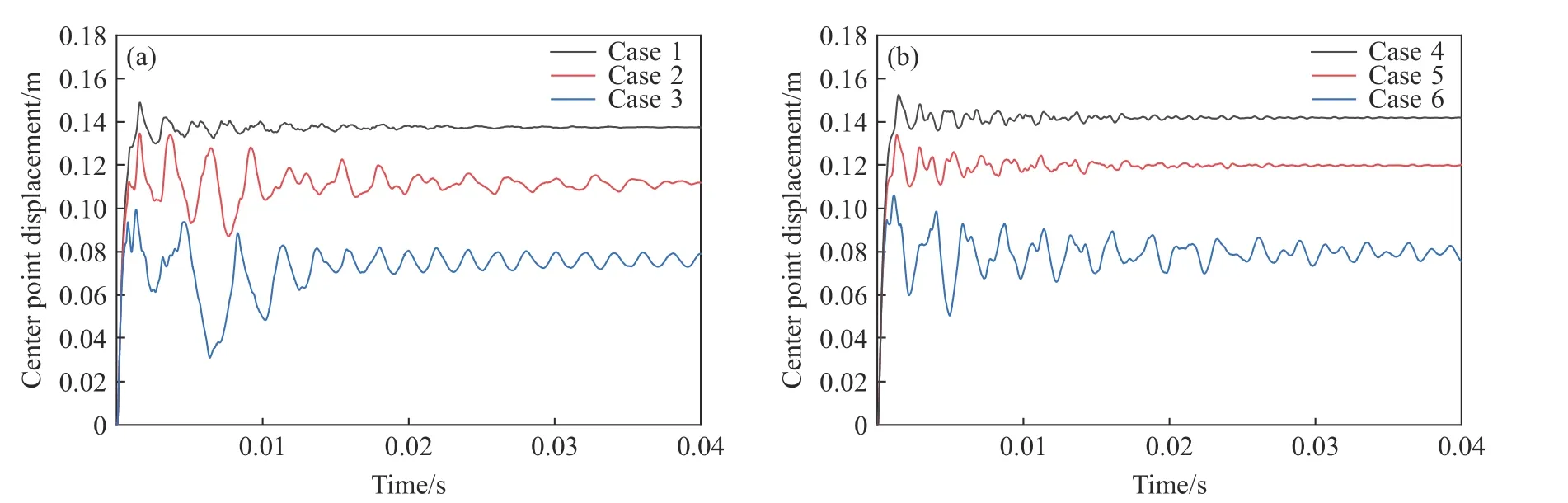
图10 各工况下有限元数值模拟得到的中心点位移-时间曲线Fig. 10 Displacement-time curves of center point by finite element simulation under various calculation cases
数值模拟计算得到的靶板中心点最大位移和最终位移与试验结果的对比如表2 所示。所有工况下有限元数值模拟结果与试验结果的相对误差均在10%以内,说明有限元模拟的空中近爆作用下固支圆板的变形结果与试验结果较吻合。
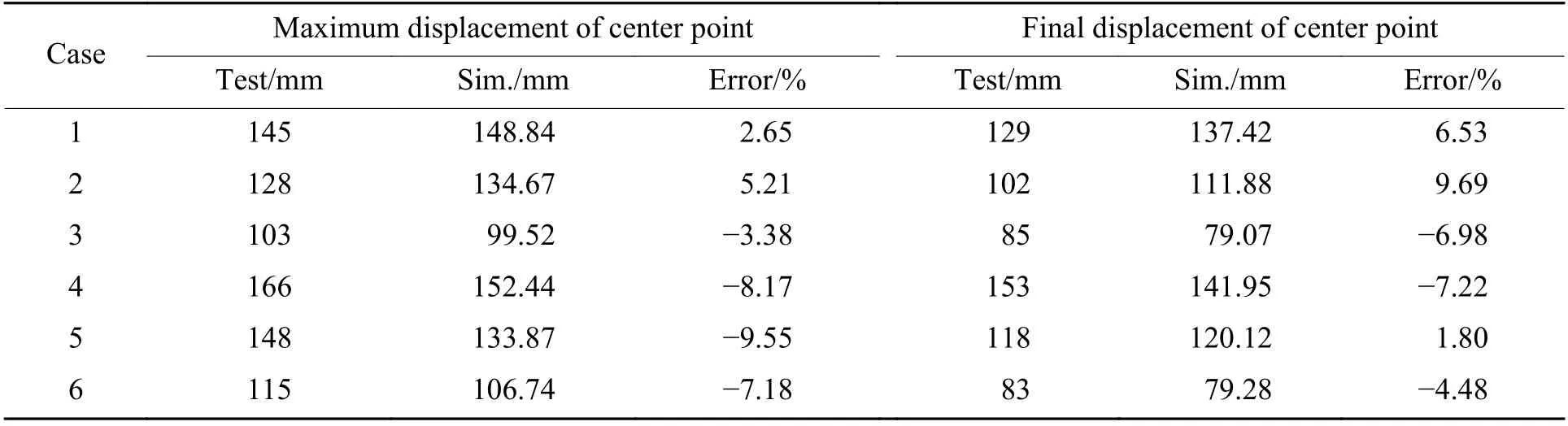
表2 各工况下试验与有限元模拟得到的中心点位移对比Table 2 Comparison of center point displacements between test and finite element simulation under various calculation cases
3 动力学模型验证
根据有限元计算结果,选取6 和10 kg TNT 空爆作用于圆板时距圆心0~0.5 mm 范围的峰值压力载荷,拟合得到的峰值压力分布函数如图11 所示。
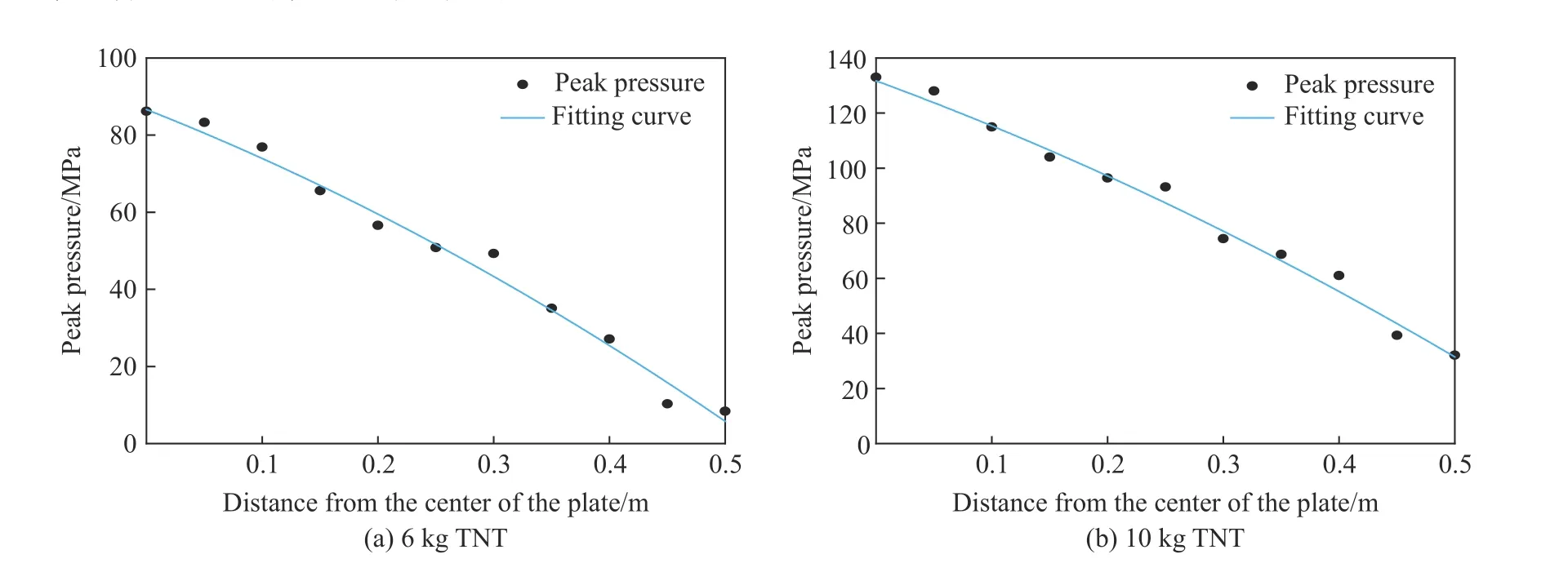
图11 峰值压力点及其拟合函数Fig. 11 Peak pressure points and fitting functions
将拟合出的函数代入式 (2) 得 到等效均匀载荷峰值,并代入式 (61) 可 得等效均匀载荷p(t)。经过拟合,得到ta=0,b=1,td=5×10-4s,6 和10 kg TNT 空爆下的等效均匀峰值压力分别为48.3 和83.7 MPa。
以工况1 为例,通过计算WPM、WPB、WPNM,可将变形过程分为5 个阶段。
(1) 阶段1(0~WPM)
在此阶段,整个圆板均未屈服,完全处于弹性状态,将等效载荷、等效质量、等效刚度、等效抗力代入运动方程


由此,通过多个阶段的叠加可以得到工况1 时固支弹塑性圆板在空爆作用下的完整动态响应。分别计算6 种工况下弹塑性圆板中心点位移随时间的变化曲线,并与数值模拟得到的圆板中心点挠度进行对比,如图12 所示。从图12 可以看出,在相同当量的爆炸载荷作用下,弹塑性圆板材料的屈服强度越高,其中心点的最大位移和最终位移越小。这是由于材料的屈服强度越高,圆板加载后期的等效刚度和等效抗力越大,中心点速度衰减得越快,从而导致中心点的最大位移和最终位移越小。近爆条件下固支弹塑性圆板的变形过程受多种因素的影响,因此,有限元数值模拟得到的弹塑性圆板中心点位移随时间变化曲线不是振幅逐渐衰减的理想的简谐振动曲线。
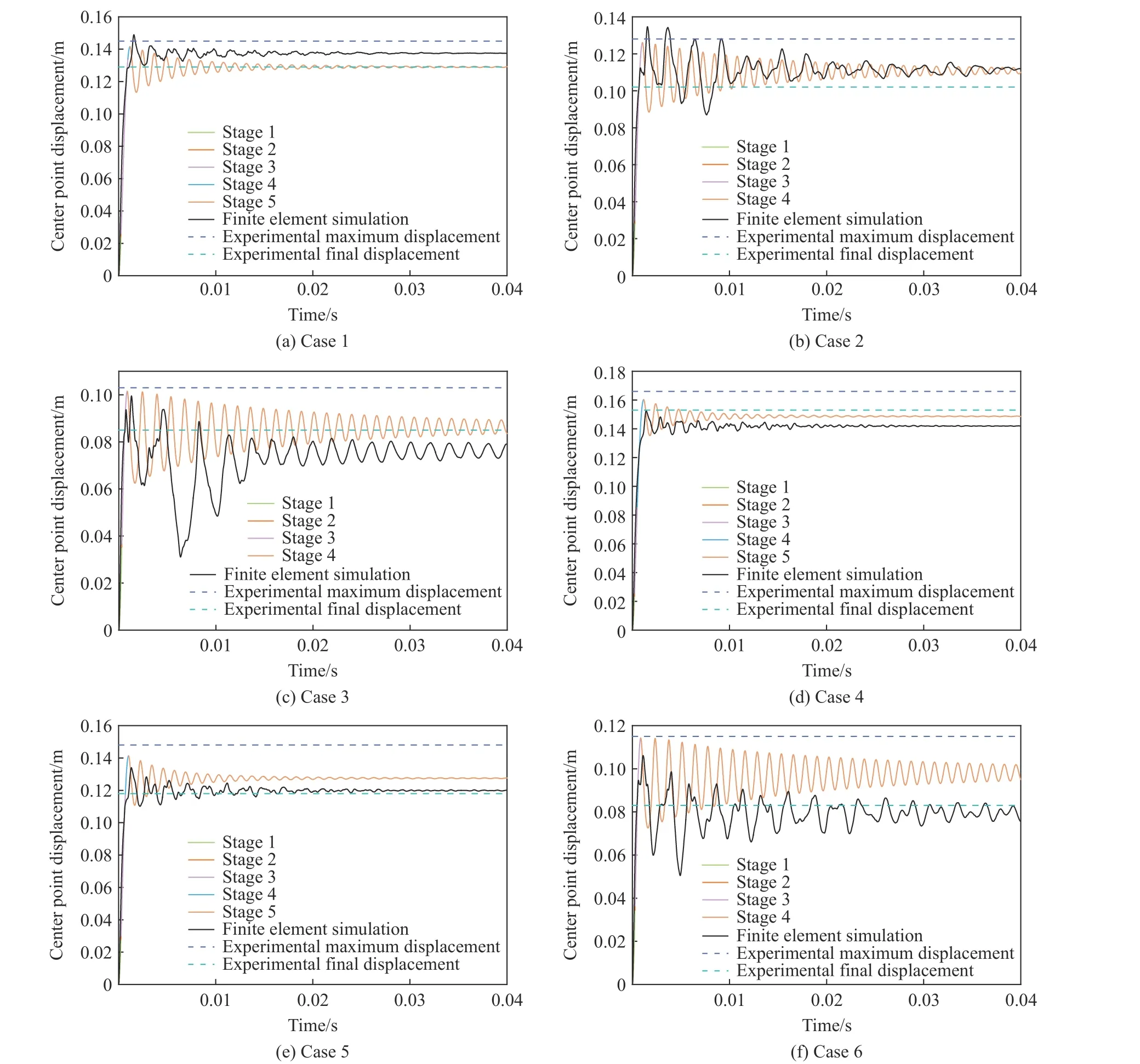
图12 各工况下动力学模型计算结果与试验及有限元数值模拟结果的对比Fig. 12 Comparison of dynamic model results with test and finite element simulation results under various cases
通过动力学模型计算各个工况的中心点位移,并与试验结果进行对比,结果如表3 所示。从表3可以看出,6 种工况下SDOF 模型计算结果与试验结果之间的误差表现出相似的趋势,即计算得到的圆板中心点最大位移相对于试验值偏小,而最终位移相对于试验值偏大,导致这些误差的原因可能有以下3 方面:(1) SDOF 模型采用固支边界条件,然而在试验中很难实现对靶板的理想刚性约束,往往会在边界处产生一定的滑移,另外,多次爆炸冲击作用后,试验台架的约束作用不可避免地减弱,导致试验测量的中心点最大位移偏大;(2) 试验中空爆载荷并非均匀载荷,爆轰产物首先作用于圆板中心,随后逐渐向周围扩散,且圆板的实际变形过程并非严格遵循形函数,导致动力学模型计算得到的中心点最大位移小于实际最大位移;(3) 由于实际的金属材料存在不同程度的应变强化效应和应变率效应,而动力学模型将材料简化为理想弹塑性本构模型,计算出的等效抗力偏小,导致求解的中心点最终位移相对于试验位移偏大。
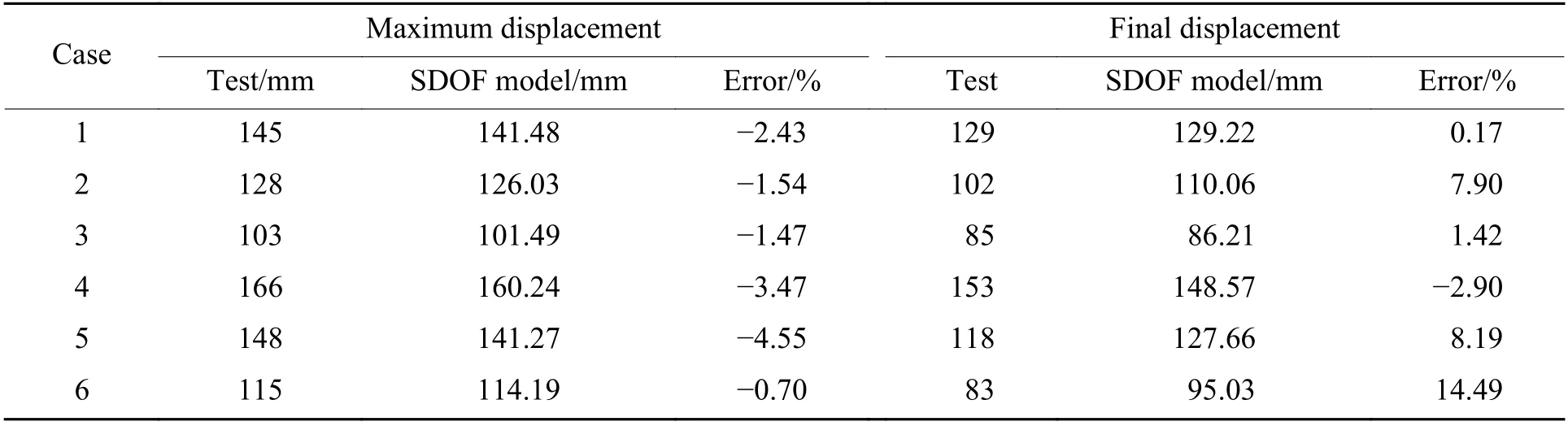
表3 各工况下动力学模型计算结果与试验结果的对比Table 3 Comparison between dynamic model results and test results under various cases
将动力学模型计算的中心点最终位移代入式 (3),得到靶板变形后的轮廓线,并与试验轮廓线进行对比,结果如图13 所示。从图13 可以看出,各工况下动力学模型计算得到的靶板轮廓线与试验结果拟合较好,因此,式 (3)可以较好地描述空中近爆作用下固支圆板的变形轮廓。
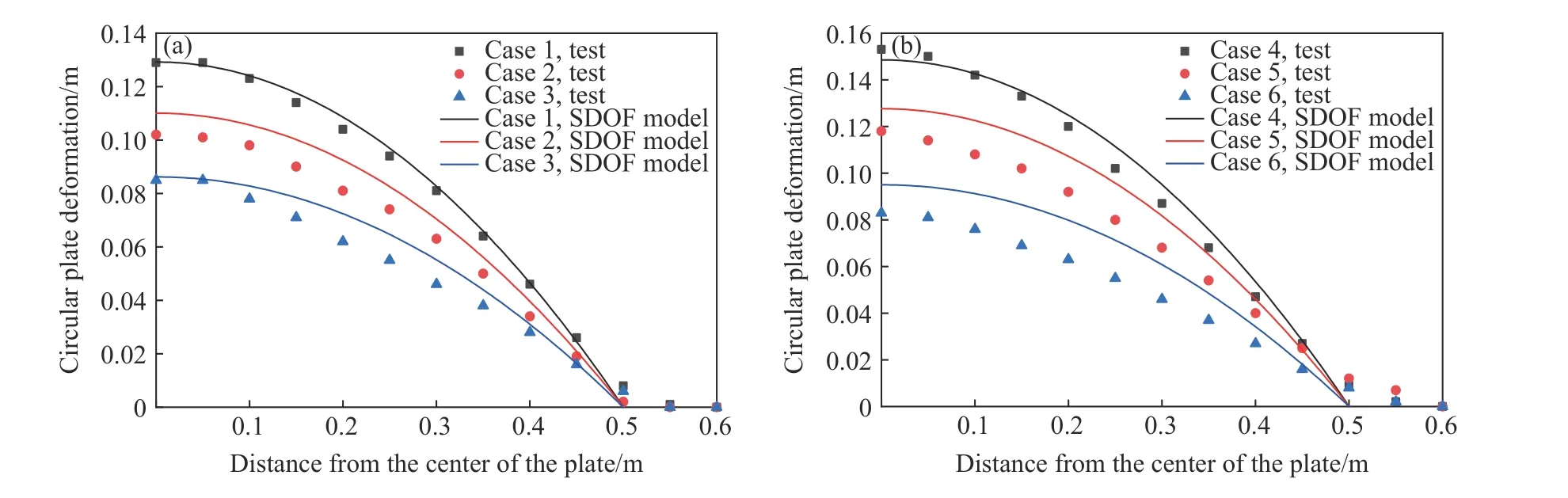
图13 各工况下动力学模型与试验得到的靶板轮廓线的对比Fig. 13 Comparison of circular plate deformations between dynamic model and test under various cases
总的来说,动力学模型计算的中心点位移与试验结果的最大相对误差未超过15%,符合工程模型的误差要求,可为结构抗爆设计提供快速算法。
4 结 论
(1) 通过6 种工况的对比分析可知,等效SDOF 模型计算结果与试验及数值模拟结果的偏差在合理范围内,采用等效SDOF 方法可以较准确地预测空爆载荷作用下固支圆板的变形情况。考虑到SDOF模型的计算效率比有限元数值模拟的计算效率高,因此,本研究发展的单自由度方法可为装甲车辆防爆结构设计提供技术支撑。
(2) 质量-弹簧-阻尼模型的计算结果是振幅逐渐衰减的简谐振动曲线。然而,由于固支圆板的实际运动过程受多种因素影响,如试验中很难做到刚性约束,台架多次爆炸冲击后难免有变形,边界约束能力减弱等,实际钢板变形并非严格按照形函数发生,并且实际材料并非理想的弹塑性,存在不同程度的应变强化效应和应变率效应,因此,SDOF 模型对系统固有频率和振幅的估计存在一定误差。
(3) 如果将固支圆板看作一个系统,空爆载荷视为系统的输入,固支圆板上各点发生的振动视为系统的输出,那么,系统动力响应分析的准确与否不仅取决于系统描述的准确性,同时还取决于输入载荷描述的准确性。由于精确描述近场爆炸载荷十分困难,因此,通过LS-DYNA 分析结果拟合得到作用在圆板上的爆炸载荷是一种可行的方法。当然,改善爆炸载荷模型精度的方法都有益于提升本研究所建立的SDOF 模型的预测结果。

