木贼属植物仿生薄壁结构的耐撞性优化
刘飞明,雷建银,乔 力,刘志芳
(太原理工大学机械与运载工程学院应用力学研究所, 山西 太原 030024)
经过亿万年的进化,自然界中的生物可以适应各种各样的复杂环境,这为人们设计高质量的吸能结构提供了大量的原型,例如竹子[1]、香蒲[2]、棕榈[3]以及人与动物的骨骼、肌腱[4-5]等。研究表明,仿生结构在耐撞性方面比传统结构更加出色。黄晗等[6]基于雀尾螳螂虾螯结构设计出一种具有仿生晶胞单元的薄壁结构,采用响应面法对该结构进行优化,得到轴向和径向上比吸能最优的结构。于鹏山等[7]受毛竹微观结构的启发,在传统双圆管结构的基础上引入双菱形肋骨,设计了一种新型仿竹薄壁管,结果表明,与传统双圆管相比,新型仿竹薄壁管在轴向载荷下的比吸能提高了83.61%,压缩力效率提高了198.65%。Huang 等[8]基于水稻茎秆结构,设计了一种弯扭耦合的仿生薄壁梁,该仿生薄壁梁可以在降低扭转约束的同时保持纵向刚度,使梁避免由于附加的小角度纤维层的扭转约束而导致弯扭耦合比降低。霍鹏等[9]基于鹿角骨单位结构特征,设计了内径相同、外径等梯度逐层递减的仿生薄壁管,并通过多项式回归元模型和多目标粒子群优化算法对该管进行了优化。白芳华等[10]基于甲虫鞘翅的微观结构,设计出多种应用于客车吸能的八边形多胞薄壁管,并通过简化的超折叠单元理论对数值模型进行验证,结果表明,所设计的八边形多胞薄壁管的耐撞性能表现优异。
木贼属植物广泛分布在各种复杂环境之中。图1[11]显示了3 种木贼属植物及其横截面,可以发现,此类植物具有很高的相似性:长径比很大,其横截面积由双管及其之间的连接肋组成。该类植物因对复杂自然环境具有良好的适应能力而引起了研究人员的关注。Yin 等[11]根据木贼属植物的结构特点,提出了一种新型的木贼属植物仿生薄壁结构(horsetail-bionic thin-walled structure,HBTS),并对该结构在侧向冲击下的耐撞性能进行了研究,结果显示,肋骨数、内径和结构整体壁厚对该结构的耐撞性有显著影响,与圆管和方管相比,该结构在横向载荷方向的耐撞性能更好。Xiao 等[12]对该新型HBTS在轴向载荷下的耐撞性能进行了研究,结果表明,轴向动态载荷下HBTS 中存在的肋骨数越多,其比吸能和最大峰值载荷越高,肋骨数为16 的HBTS 具有最佳的整体耐撞性。Yin 等[13]对HBTS的泡沫填充结构在侧向冲击下的耐撞性能进行了研究,分析了整体壁厚、泡沫材料密度以及加载位置对该结构耐撞性能的影响,并对设计参数进行了鲁棒性优化。但在文献[11-13]中,研究人员只考虑了HBTS的整体壁厚以及内径和肋骨数对耐撞性能的影响,并未研究HBTS 各部分壁厚不相等时的情况。

图1 3 种木贼属植物:(a)沼泽问荆,(b)野生问荆,(c)斑纹木贼[11]Fig. 1 Three horsetails: (a) Marsh horsetail, (b) field horsetail and (c) variegated horsetail[11]
本研究集成ABAQUS 有限元软件与modeFRONTIER 优化软件,对HBTS 在侧向冲击下的耐撞性能进行优化,综合考虑外管壁厚、肋骨壁厚、内管壁厚、内径和肋骨数5 个设计参数对HBTS 耐撞性能的影响,以寻求工程所需的最优结构。首先构建典型的薄壁圆管模型,然后验证有限元建模方法的有效性,再分析HBTS 的整体壁厚、肋骨数和内径对耐撞性能的影响。在此基础上采用全因子实验设计方法,在设计空间上均匀选取3 750 组样本点,通过参数化建模建立有限元模型,使用基于Kriging 代理模型(KRG)的多目标优化方法对该结构进行优化,分析所获取的Pareto 前沿面上各HBTS 的设计参数分布情况,通过有限元模拟验证最优设计。
1 仿真建模与实验验证
1.1 HBTS 模型
HBTS 模型及其载荷条件如图2 所示。HBTS 的长度以及外径分别为300 和46 mm,直径为10 mm的圆柱形冲头以v=3.8 m/s 的速度撞击结构中跨。图2(b)展示了HBTS 的截面形状以及选择优化的5 个设计参数,分别为HBTS 的外管壁厚tR、肋骨壁厚tI、 内管壁厚tr以及肋骨数n和内径d。
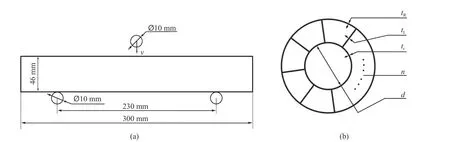
图2 模型的载荷条件(a)和横截面(b)Fig. 2 Load condition (a) and cross section (b) of the model
1.2 有限元模型及其有效性
1.2.1 有限元模型
采用有限元软件ABAQUS 进行数值分析。有限元模型采用四节点减缩积分壳单元(S4R),厚度方向设有5 个积分点。冲头和支架设置为刚体,摩擦系数为0.2。HBTS 的基体材料采用铝合金AA6061[14],其力学性能参数见表1。为了得到最佳的单元尺寸,对tR、tI、tr均为0.5 mm,肋骨数n为16,内管直径d为10 mm 时的有限元模型进行了5 种不同网格尺寸的收敛性验证,网格收敛结果如图3 所示。经过计算,对于单元尺寸为1.0 和1.5 mm 的数值模型,其吸能量之间的相对偏差小于2.2%。综合考虑计算成本与数值模型精度后,采用1.5 mm 的网格尺寸模拟该仿生薄壁结构。

表1 铝合金AA6061 的材料参数Table 1 Parameters of aluminum alloy AA6061
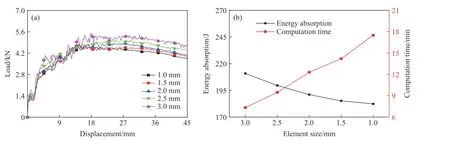
图3 网格收敛结果:(a)载荷-位移曲线, (b)吸能量和计算时间Fig. 3 Mesh convergence results: (a) load-displacement curves, (b) energy absorption and computation time
1.2.2 模型有效性验证
Sun 等[14]对普通圆管在侧向冲击载荷下的变形模式进行了研究,在其实验中,直径为10 mm、质量为14.44 kg、初始速度为3.44 m/s 的圆柱形冲头撞击普通圆管的中跨。为了验证有限元模型的有效性,使用ABAQUS 建立了与其具有相同载荷条件的有限元模型。图4 显示了实验与有限元模拟结果的对比。可以看出,模拟的变形模式与实验的变形模式相同,载荷-位移曲线中的最大峰值载荷接近,变化趋势一致,证明了所用建模方法的有效性。
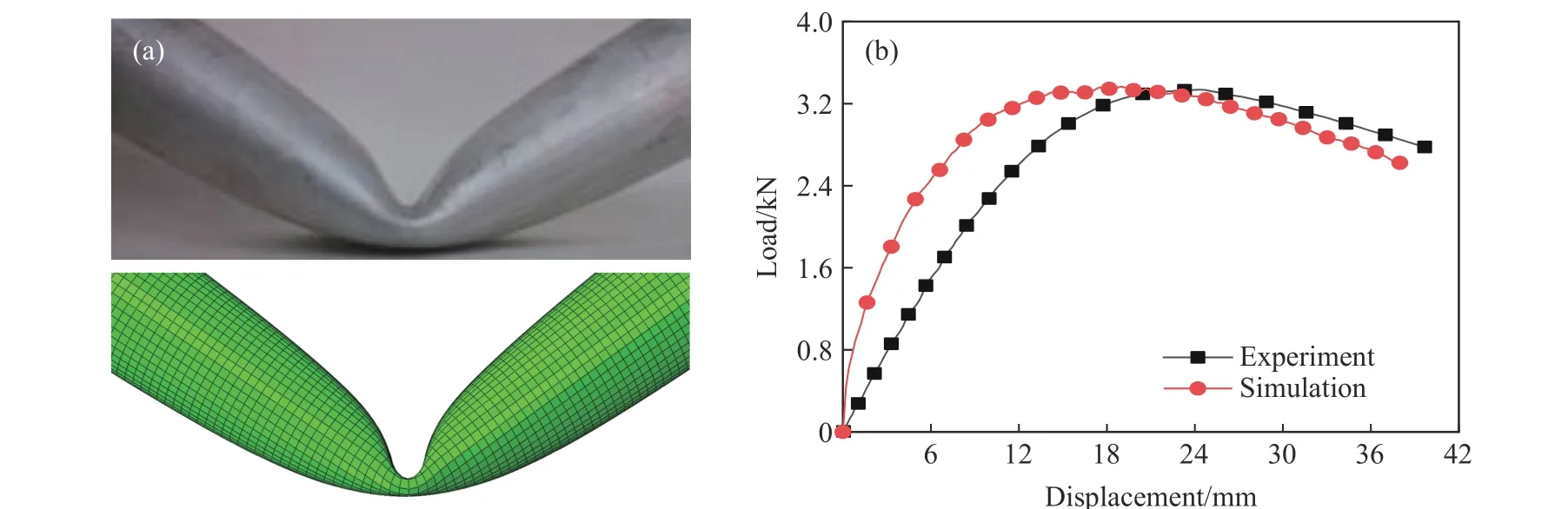
图4 实验[14]与有限元模拟的比较:(a) 变形模态,(b) 载荷-位移曲线Fig. 4 Comparison between experiment[14] and finite element simulation: (a) deformation mode, (b) load-displacement curves
2 HBTS 的耐撞性分析
2.1 结构耐撞性能评价指标
为了评估结构的耐撞性,必须确定耐撞性评价标准。吸能量(energy absorption,EA)、比吸能(specific energy absorption,SEA) 、最大峰值载荷(peak load,Fmax) 以及碰撞力效率(crash force efficiency,CFE)是冲击动力学中薄壁结构吸能特性的重要评价指标。比吸能表示单位质量结构吸收的能量,比吸能越高,结构的能量吸收能力越好,其公式[15]为

2.2 肋骨数、内径与整体壁厚对耐撞性的影响
当HBTS 3 个部分的壁厚tR、tI、tr一致时,肋骨数n、内径d、整体壁厚t对耐撞性的影响(整体壁厚t=tR=tI=tr),如图5、图6、图7 所示,其中为了更好地对HBTS 的耐撞性能进行标准性评判,碰撞位移皆取46 mm。可见,HBTS 的整体壁厚、肋骨数以及内径对HBTS 的耐撞性能有很大影响。对比图5 和图6可知,增加肋骨数和整体壁厚会明显提高HBTS 的SEA和Fmax。例如:当n=6、d=10 mm 时,随着整体壁厚t的增加,SEA和Fmax增 加,整体壁厚t为0.1、0.8 和1.5 mm 时,HBTS 的SEA分别为0.21、0.95 和1.28 J/g,Fmax分 别为0.15、4.45 和11.04 kN;但是当d=10 mm 时,n=14 的HBTS 的SEA均优于n=16 的HBTS,说明当内径较小(d=10 mm)时,肋骨数从14 变化到16 增加了结构的质量,但不会大幅提高其吸能量。
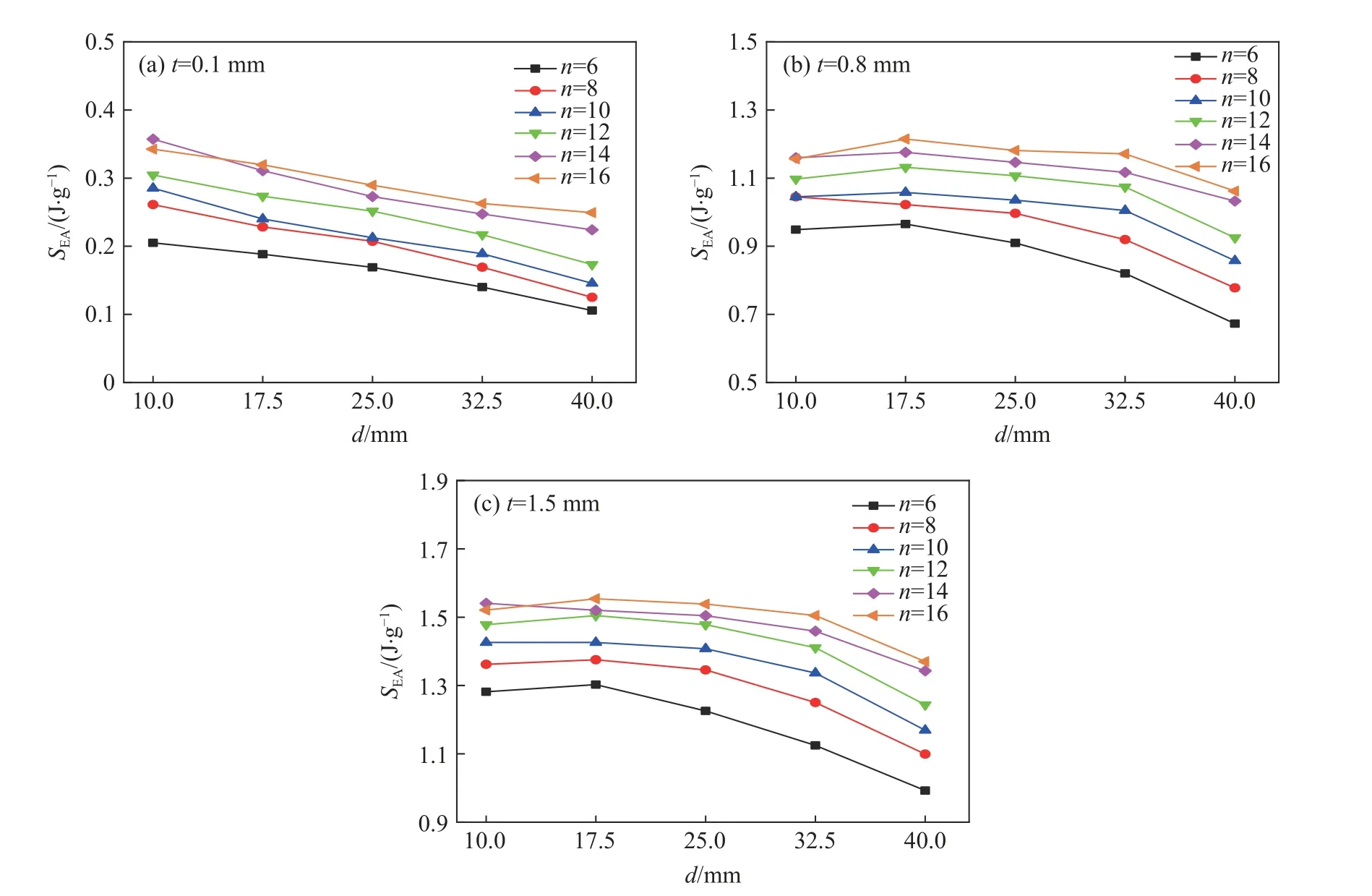
图5 n、d 和t 对S EA的影响Fig. 5 Effects of n, d and t on SEA
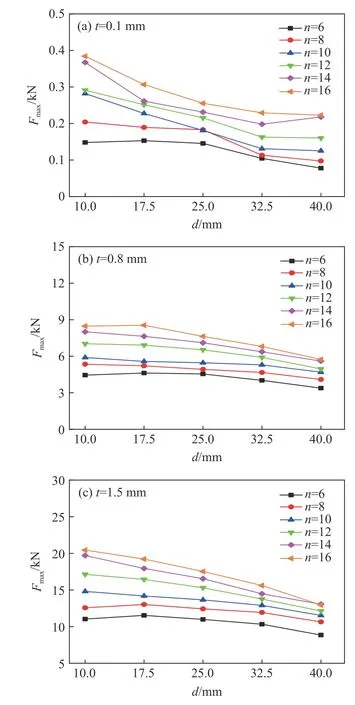
图6 n、d 和t 对 F max的影响Fig. 6 Effects of n, d and t on Fmax
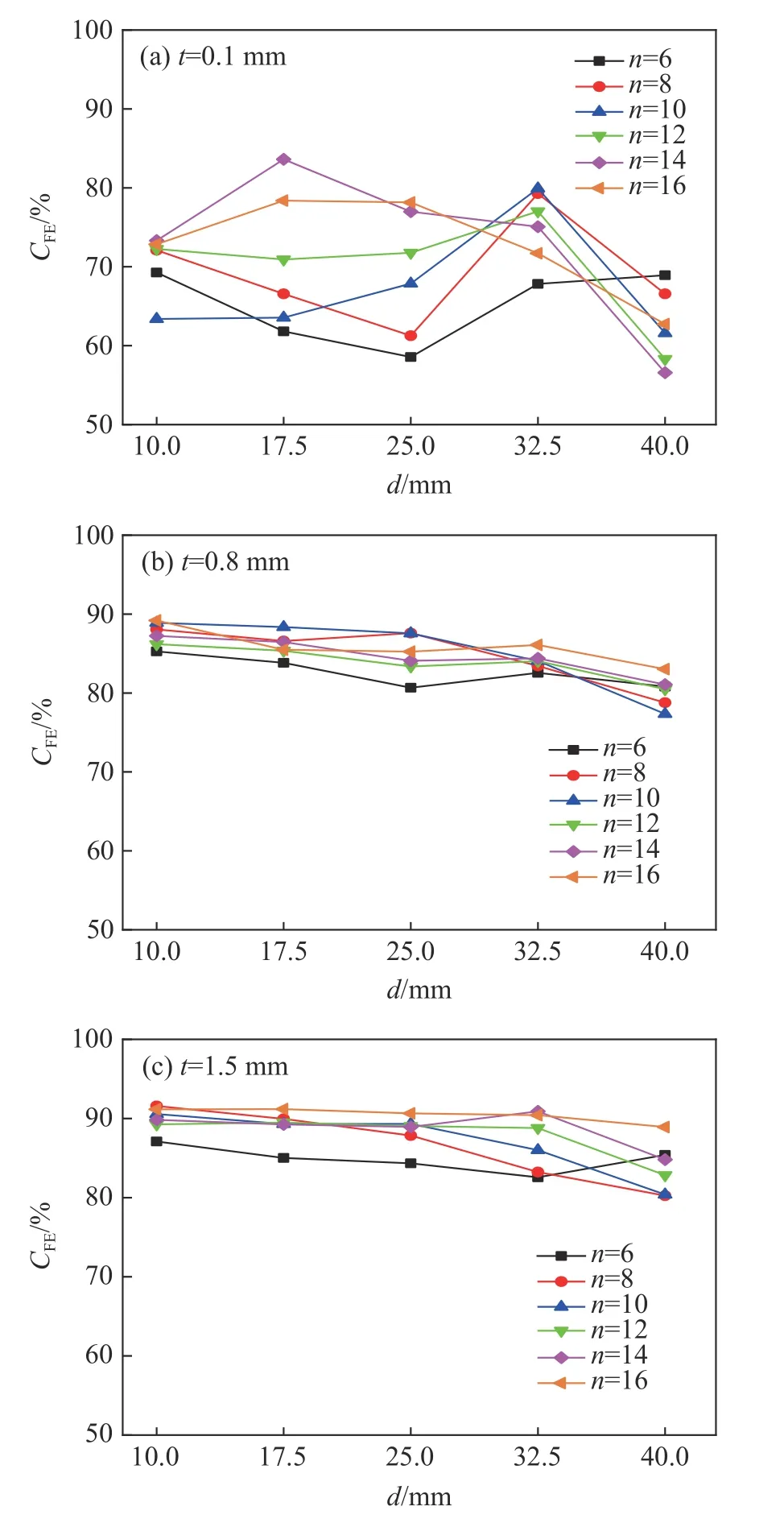
图7 n、d 和t 对C FE的影响Fig. 7 Effects of n, d and t on CFE
另外,尽管SEA随 着肋骨数以及整体壁厚的增大而增大,但是Fmax也会相应地增大,在工程实际中应该避免过高的Fmax, 以提高结构的安全性能。由图6 可知,增大内径会降低Fmax,这是由于内径的增大减小了HBTS 的总质量。而由图5(b)和图5(c)可知,当t为0.8 和1.5 mm 时,SEA在内径区间为10~25 mm时的变化幅度较平缓,即增加内径可以在不损失比吸能的情况下降低最大峰值载荷。
从图7 可以看出,CFE对 于壁厚、肋骨数以及内径的变化不敏感。当t=0.1 mm 时,CFE随着肋骨数和内径的变化呈不规则分布。当t=0.8 mm 和t=1.5 mm 时,CFE随着内径的增大缓慢减小,随着肋骨数以及整体壁厚的增大而略微增大。
2.3 壁厚对HBTS 变形模态和耐撞性能的影响
图8 显示了两种质量的HBTS 在各部分壁厚不同时的整体变形模态以及当载荷施加时间为4.04、8.07 和12.11 ms 时横截面的变形模态。其中结构a、b 和c 的质量M为110.2 g,结构d、e 和f 的质量M为308.1 g,这些HBTS 的肋骨数n均为12,内径d均为25 mm。表2 列出了结构a~结构f 3 个部分的壁厚、质量、比吸能、吸能量等情况。
由图8 和表2 可以看出,对于质量相同的HBTS,各部分壁厚的变化会产生截然不同的变形模式。结构a 的外管壁厚(0.800 mm)是肋骨壁厚(0.100 mm)以及内管壁厚(0.100 mm)的8 倍,所以主要通过外管的弯曲变形吸收能量,内管与肋骨只起到少许支撑作用。结构b 的肋骨壁厚(0.800 mm)是内外管壁厚(0.158 mm)的5.1 倍,其变形主要集中在内外管壁的褶皱变形,壁厚较大的肋骨变形很小,只产生了较大的相对位移,所以该结构的吸能量EA( 28.02 J)和SEA(0.254 J/g)较结构a 和结构c 低,在耐撞性设计中应该避免出现这种情况。结构e 的肋骨壁厚同样大于内外管壁厚,但其EA(390.85 J)和SEA(1.268 J/g)优于同质量的结构d 与结构f,变形模态也不同于结构b,这可能是由于结构e 各部分壁厚的占比差距(肋骨壁厚为内外管壁厚的1.75 倍)较结构b 小的缘故,使得结构的变形模态发生改变,从而提高了结构的吸能特性。结构c 的外管壁厚和肋骨壁厚均为0.271 mm,小于内管壁厚(0.800 mm),其变形最初发生在壁厚较小的外管和肋骨上,当载荷施加时间为4.04 ms 时,壁厚较大的内管几乎没有参与变形,当载荷施加时间为8.07 和12.11 ms 时,内管的变形程度也远小于结构a 和结构b,所以该结构的EA(49.11 J)同样较低,为结构a(70.16 J)的70.0%。结构f 的外管壁厚(0.971 mm)和肋骨壁厚(0.971 mm)同样小于内管壁厚(1.500 mm),内管的横截面变形程度在相同时刻下也小于同质量的结构d 及结构e,EA( 315.82 J)、SEA( 1.025 J/g)以及Fmax(8.110 kN)均小于结构d 和结构e。
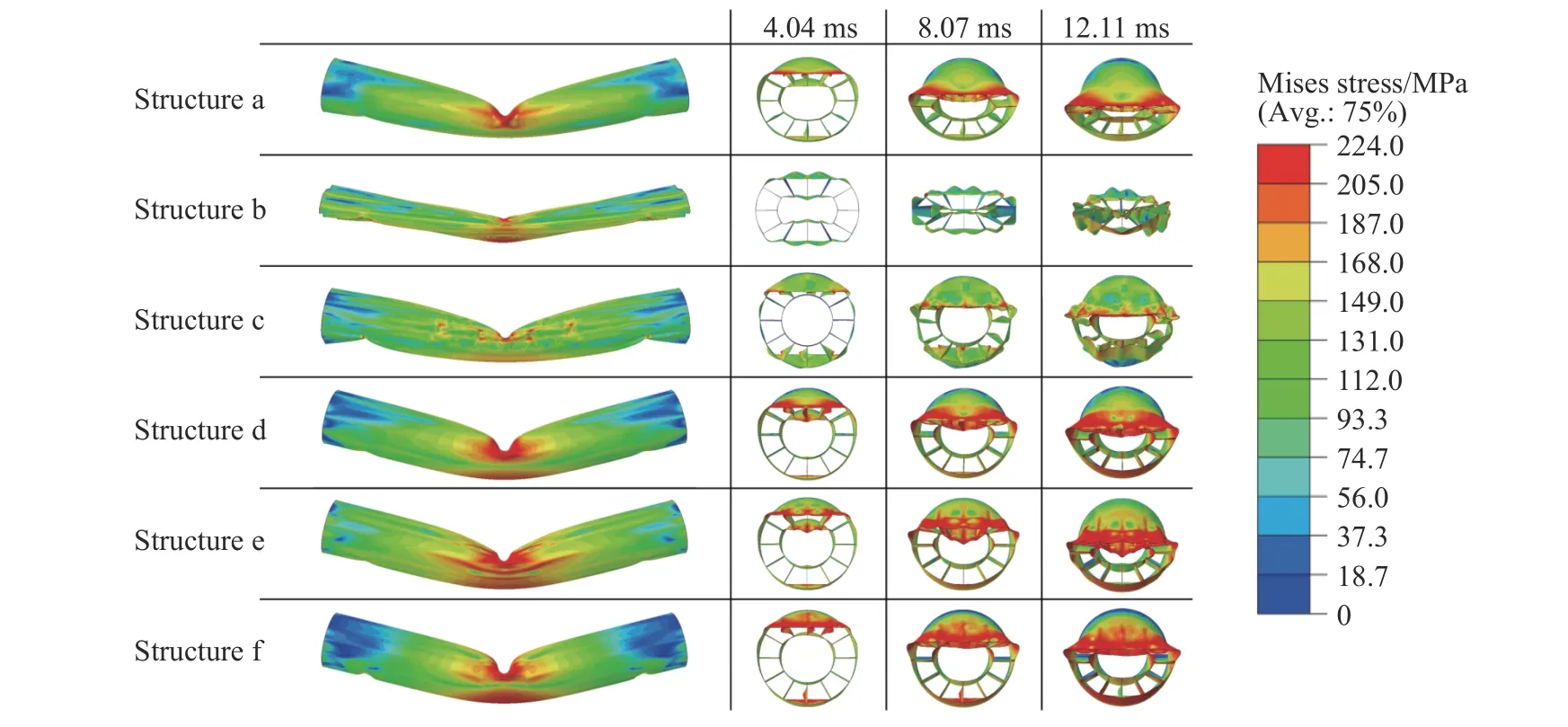
图8 不同壁厚下HBTS 的变形模态Fig. 8 Deformation modes of HBTS with different wall thicknesses
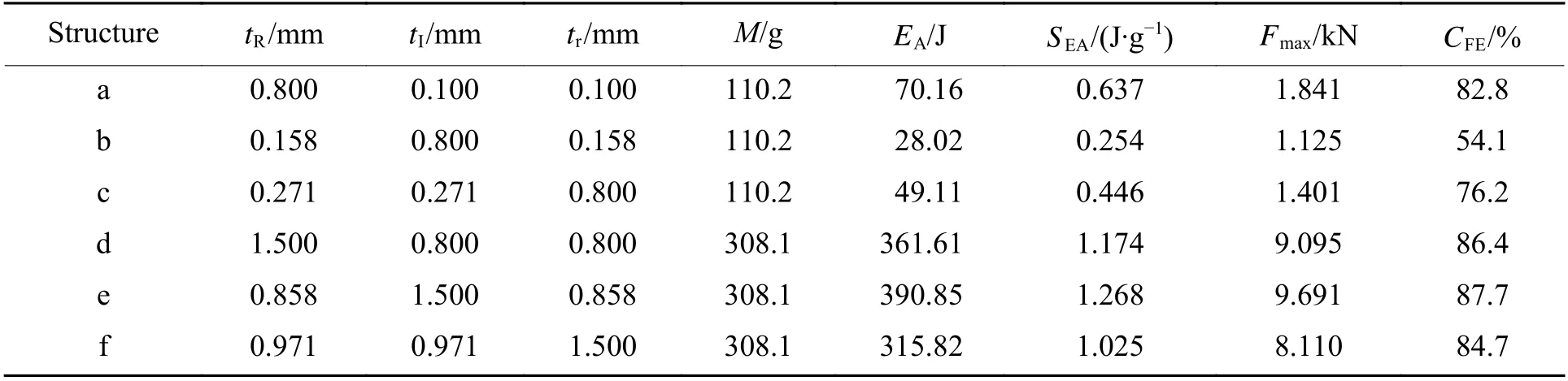
表2 HBTS 的耐撞性比较Table 2 Comparison of crashworthiness of HBTS
对比结构a~结构f 可以发现,HBTS 3 个部分的壁厚差异会对变形模态产生显著影响,进而影响其耐撞性能。因此,若要设计工程所需的最优结构,不仅需要考虑内径和肋骨个数,HBTS 中3 个部分的壁厚同样需要进行优化设计。
3 多目标优化设计
3.1 优化问题的定义
在碰撞优化问题中,EA、SEA、Fmax都 是具有重要意义的评价指标,EA、SEA作为目标函数,应该尽可能使其最大化,而Fmax是衡量结构所具有的缓冲性能的另一个指标,应该使其最小化[17]。为了综合考虑图2(b)所示的HBTS 横截面的5 个设计参数对其耐撞性能的影响,实现SEA最 大化和Fmax最小化的目标,所定义的优化问题可以表示为
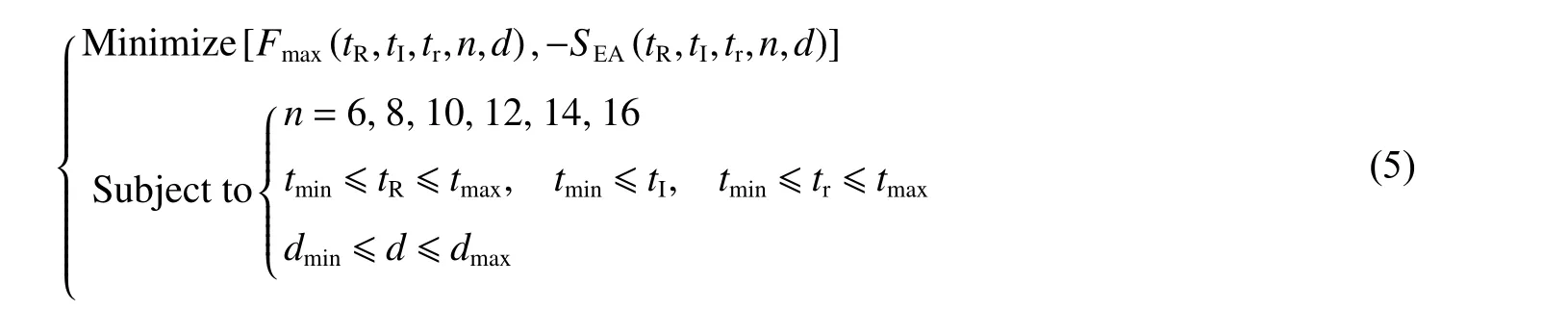
HBTS 的tR、tI、tr的设计域为(0.1 mm,1.5 mm),结构内径尺寸d的设计域为(10 mm,40 mm)。
3.2 优化流程
多项式响应曲面法和Kriging 方法[18]是工程中使用较多的构建代理模型的方法,其中Kriging法在非线性问题上经常有更加准确的结果。集成modeFRONTIER 优化软件与ABAQUS 有限元分析软件,采用基于Kriging 代理模型的多目标优化方法解决式(5)所示的优化问题,其流程图如图9所示。首先采用全因子试验设计方法(design of experiment,DOE)在设计空间生成样本点,通过参数化建模构建并计算样本点的有限元模型,提取数据后,基于样本点的数据建立目标函数的Kriging 代理模型。相比于其他多目标优化算法,多目标粒子群优化算法(multi-objective particle swarm optimization,MOPSO)具有收敛速度快、Pareto 前沿分布均匀的优点。本研究的多目标优化方法将采用Kriging 代理模型结合MOPSO 算法获取Pareto 最优解。
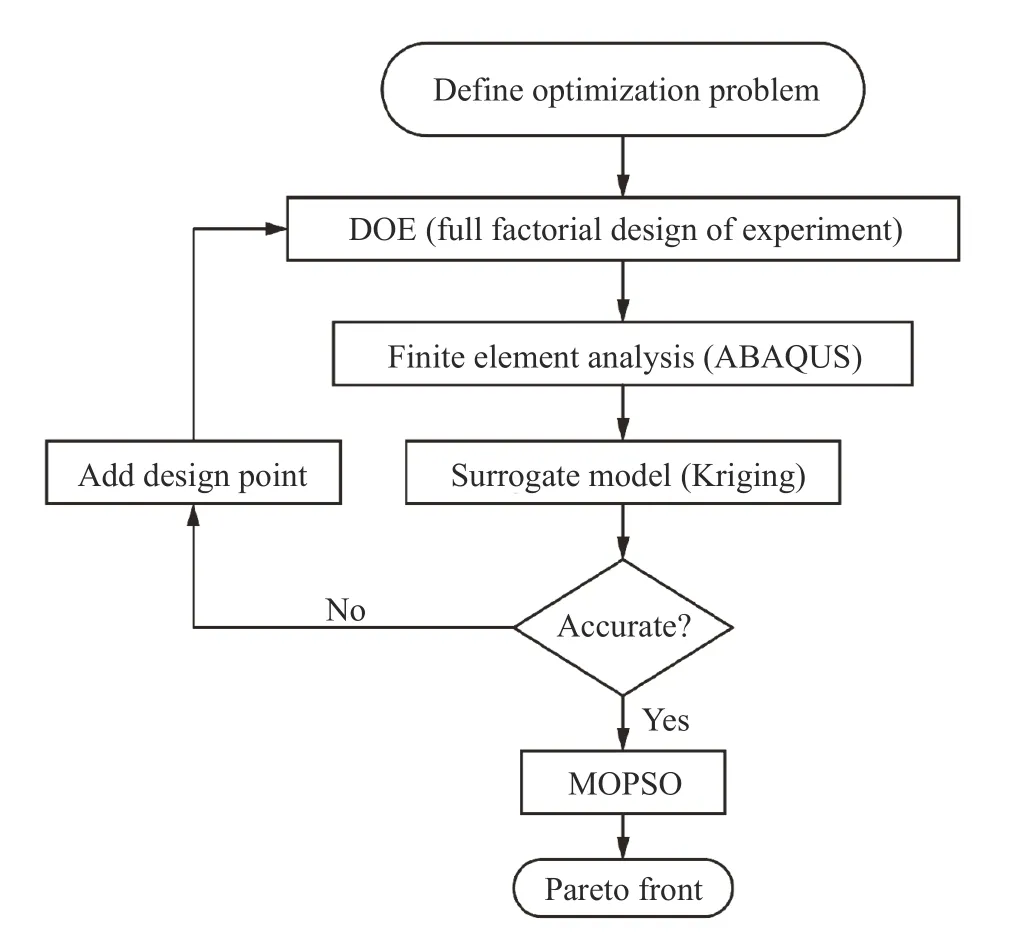
图9 多目标优化流程图Fig. 9 Multi-objective optimization flow chart
3.3 试验设计
采用全因子试验设计方法选取样本点,将内径、外管壁厚、肋骨壁厚和内管壁厚分为5 个等间距水平,如表3 所示,最终在设计空间均匀选取了3 750 组样本点。采用随机法在设计空间随机选取200 组样本点,用于后续代理模型的验证。
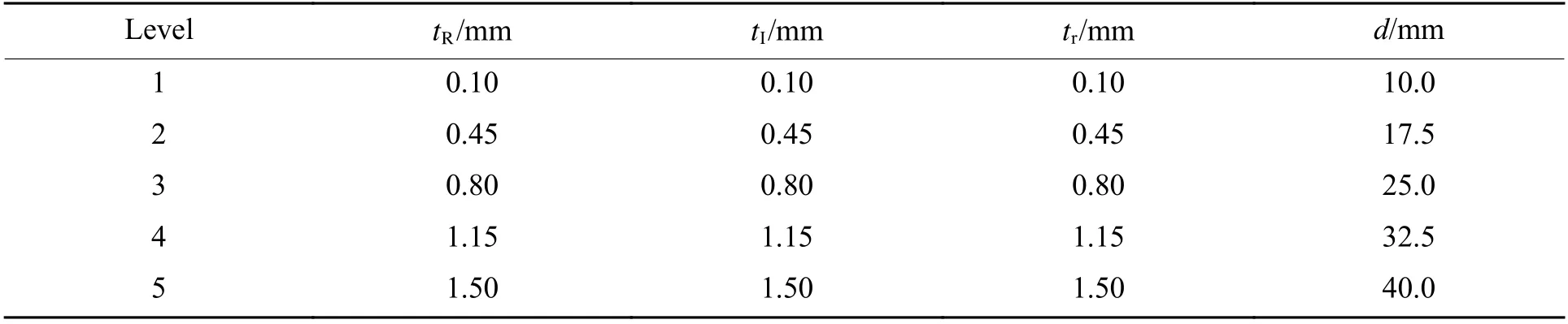
表3 壁厚与内径水平Table 3 Wall thickness and inner diameter level
3.4 代理模型及其误差度量

4 优化结果与讨论
4.1 代理模型精度
表4 列出了所构建的Kriging 代理模型的精度。可以看出,SEA和Fmax的 拟合优度R2分别为0.989 和0.997,都接近1,平均相对误差均小于1.7%,说明所构建的Kriging 代理模型是可靠的。

表4 Kriging 代理模型精度Table 4 Accuracy assessment of the Kriging surrogate models
4.2 多目标优化结果
图10 中黑色点是采用Kriging 代理模型结合MOPSO 算法优化后所获取的Pareto 前沿面,红色点为3 750 组实体点所形成的Pareto 前沿面。可以看出,由Kriging 代理模型得到的Pareto 前沿面足够连续且与实体点贴合紧密,说明MOPSO 算法能很好地收敛于最优解,工程设计人员可以根据该前沿面寻找工程所需的极值点。
图11 给出了图10 中黑色虚拟点的5 个设计参数分布情况。可以发现,该前沿面上HBTS 的5 个设计参数呈现一定的规律,整体上各个部分的壁厚呈现由小变大的趋势,当SEA小于1.0 J/g时,tI保 持最小值0.1 mm,tR和tr逐渐增大至0.9 mm,内径d保持最小值10 mm,肋骨数经过振荡之后保持为14 或16;当SEA大于1.0 J/g 时,肋骨壁厚快速增长至最大值1.5 mm,tR和tr减小至0.7 mm 后快速增加,肋骨数n保持为16,内径由最小值10 mm 快速增加至35 mm 后缓慢减小。

图10 SEA 和Fmax 的Pareto 前沿Fig. 10 Pareto front of SEA and Fmax
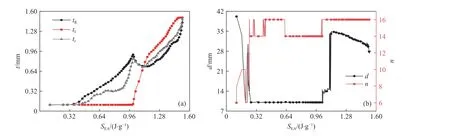
图11 Pareto 前沿面上各HBTS 的参数分布:(a) 壁厚分布,(b) 内径和肋骨数分布Fig. 11 Parameter distribution of each structure on the Pareto front:(a) distribution of wall thickness,(b) distributions of inner diameter and number of ribs
可以发现,内管壁厚tr的大小一直介于外管壁厚tR与 肋骨壁厚tI之间,肋骨数为14 或16 的HBTS具有更加优异的整体耐撞性。该Pareto 前沿面上各个HBTS 的参数分布情况为工程人员设计性能更加优良的吸能结构提供了一定的参考价值。
4.3 不同 Fmax限制下的最优解
设计人员可以根据需求从Pareto 最优解中选取最适合的结构。图12 给出了将Fmax限制在5 和10 kN 时两个最佳HBTS 的载荷-位移曲线,其设计参数见表5。结果表明,两个模型的有限元(finite element,FE)分析结果与代理模型近似结果的相对偏差 δSEA和 δFmax均小于2.73%。
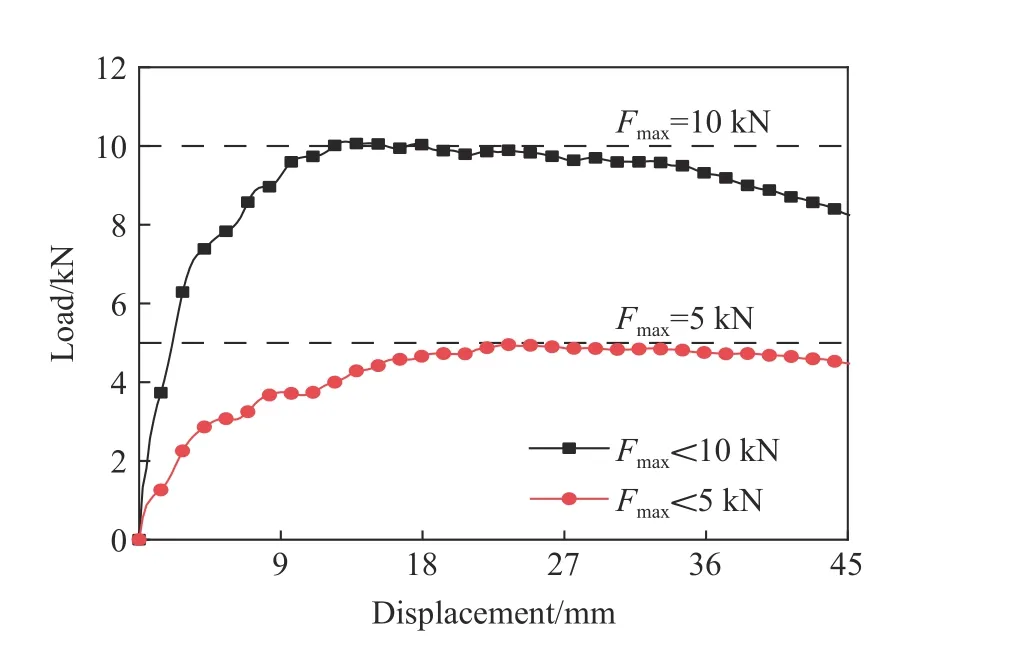
图12 不同 F max限制下最优HBTS 的载荷-位移曲线Fig. 12 Load-displacement curves of optimal HBTSs with different F max limits

表5 不同 Fmax限制下的最优HBTSTable 5 Optimal HBTSs with different F max limits
5 结 论
通过ABAQUS 有限元分析软件建立了HBTS在侧向冲击载荷下的有限元模型,并验证了其准确性,分析了整体壁厚、内径和肋骨数对HBTS 耐撞性能的影响以及HBTS 3 个部分的壁厚变化对变形模态的影响。通过集成modeFRONTIER 优化软件与ABAQUS 有限元分析软件,建立了大量有限元模型,基于此构建了比吸能和最大峰值载荷的Kriging 代理模型,采用基于Kriging 代理模型的多目标优化方法,对该结构的5 个设计参数进行优化,获得了Pareto 前沿面,分析了Pareto 前沿面上各结构的5 个设计参数的分布情况,并用有限元模拟验证了该前沿面的准确性,得到如下主要结论。
(1)内径、整体壁厚以及肋骨数对结构的耐撞性有显著影响。SEA和Fmax随着肋骨数以及结构整体壁厚的增加而增加。当t较大时,适当增加内径可以提高安全性能而不会降低结构的SEA。CFE对于整体壁厚、肋骨数以及内径的变化不敏感。
(2) HBTS 各个部分的壁厚变化会显著影响其变形模态,进而影响结构的EA、SEA和Fmax。
(3)所构建的SEA和Fmax的Kriging 代理模型的拟合优度分别为0.989 和0.997,平均相对误差均小于1.7%,验证了代理模型的有效性。
(4)由MOPSO 优化算法得到的Pareto 前沿面中各个HBTS 内管壁厚均介于外管壁厚与肋骨壁厚之间,肋骨数为14 或16 的HBTS 具有更加优异的整体耐撞性。

