7 大晶系的力学稳定性判据及其应用：以SiO2 为例

高 娟，刘其军，蒋城露，樊代和，张 淼，刘福生，唐 斌

（1. 西南交通大学物理科学与技术学院, 四川 成都 610031；2. 四川农业大学水利水电学院, 四川 雅安 625014；3. 西北工业大学材料学院, 陕西 西安 710072）

人类对晶体几何形状的探索与认识可以追溯到石器时代，但直到17 世纪的晶体研究才从矿物学走向晶体学，并在X 射线晶体学创立后得以迅速发展[1-6]。根据对称性，晶体可分为7 大晶系、14 种布拉伐格子、32 种点群、230 种空间群，其中7 大晶系包括三斜、单斜、正交、四方、三角、六角和立方晶系。1940 年，Born[7]开启了晶格力学稳定性的研究工作，并与黄昆一起确立了Born 稳定性准则[8]。直到今天，该准则仍被广泛应用于晶格力学稳定性判断[9-13]。2014 年，Mouhat 等[14]进一步讨论了7 大晶系稳定性的充分必要条件，得到了正交、四方、三角、六角和立方晶系的稳定性判据表达式，并指出了此前文献中推导出的单斜晶系的力学稳定性判据的错误。该工作是目前最准确的结果，已被广泛应用于晶体力学稳定性判断。然而，由于低对称的三斜和单斜晶系的判据表达式太复杂，他们并未给出。

二氧化硅（SiO2）作为自然界中广泛存在的物质，在半导体物理、材料科学、地球物理、信息光电子等领域应用广阔[15-16]。此外，SiO2具有多种晶型（包括常压石英、鳞石英、方石英系列）以及众多高压相（如柯石英、斯石英（金红石型）、氯化钙型（CaCl2）、氧化铅型（α-PbO2）、黄铁矿型（FeS2）、氯化铅型（α-PbCl2）等[17-18]）。这些晶型覆盖了7 大晶系，是运用推广力学稳定性判据的候选体系之一。

本研究首先推导单斜和三斜晶系的力学稳定性判据，作为Mouhat 和Coudert 推导结果的补充；然后，以SiO2为例，采用各种力学稳定性判据，通过第一性原理计算出9 种SiO2的弹性常数；最后，根据推导出来的力学稳定性判据研究这9 种SiO2的力学稳定性。

1 7 大晶系力学稳定性判据的推导

众所周知，晶体原子的周期性排列产生晶体的宏观对称性，可由32 个点群概括，加上平移对称性，晶体结构的对称性则有230 个类型，即230 种空间群。7 大晶系的点群个数及符号、空间群个数及编号以及独立矩阵元数目如表1 所示，其中nCi j为独立弹性常数的个数。根据弹性常数矩阵正定的充分必要条件（矩阵的所有顺序主子式为正），可以推导出7 大晶系的力学稳定性判据。

表1 7 大晶系的点群个数及符号、空间群个数及编号以及独立弹性常数的个数Table 1 Quantites and symbols of point groups and space groups, and the quantities of independent elastic constants for the seven crystal systems

1.1 立方晶系

1.2 六角晶系

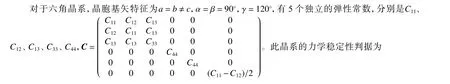
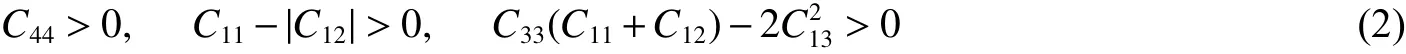
1.3 三角晶系

1.4 四方晶系

1.5 正交晶系

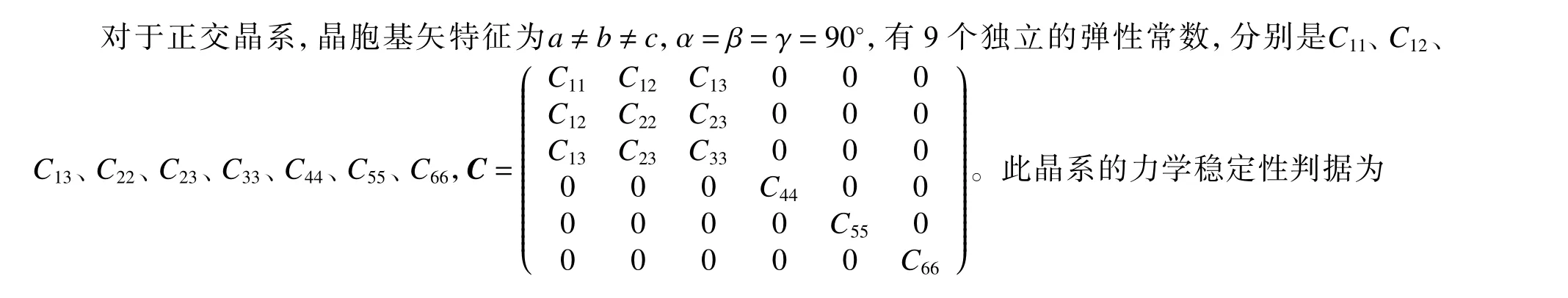
1.6 单斜晶系

1.7 三斜晶系

根据正定矩阵的充分必要条件证明矩阵的正定性有多种方法，鉴于单斜和三斜晶系弹性矩阵较复杂，本研究只采用其中最简单且方便的一种方法进行推导，即各阶顺序主子式为正的矩阵为正定矩阵。与之等价的另一个充分必要条件是“矩阵的所有主子式为正”，这一条件要求Cii＞0。 由于Cii＞0这一要求与式(11)和式(12)中的部分条件重复，因此未单独列出，但是该要求对于任意弹性矩阵来说都是必要的，且非常容易判断，所以在衡量晶体的力学稳定性时可以根据这一必要条件对计算出来的弹性矩阵的正定性进行初步的预判。

2 基于稳定性判据的SiO2 稳定性分析

2.1 计算方法和理论模型

采用Materials Studio 软件中的CASTEP[25]模块对SiO2在0 GPa 下进行结构优化和弹性常数计算，此模块是基于密度泛函理论（density functional theory，DFT）[26-27]第一性原理的量子力学计算程序。交换关联势由GGA 下的Perdew-Wang 1991（PW91）[28]泛函进行计算。所有结构的计算均采用超软赝势（ultrasoft pseudopotential），能量收敛精度为平均每个原子的能量5.0×10-6eV，最大应力为0.01 eV/Å，最大偏移为5.0×10-4Å，SiO2中Si 3s23p2和O 2s22p4视为价电子。

2.2 计算结果与讨论

图1 列出了属于不同空间群的9 种SiO2经过几何优化后的晶体结构及其晶格参数。在该基础上计算的相应弹性常数结果列于表2，表2 中第1 列为不同结构的SiO2的空间群。

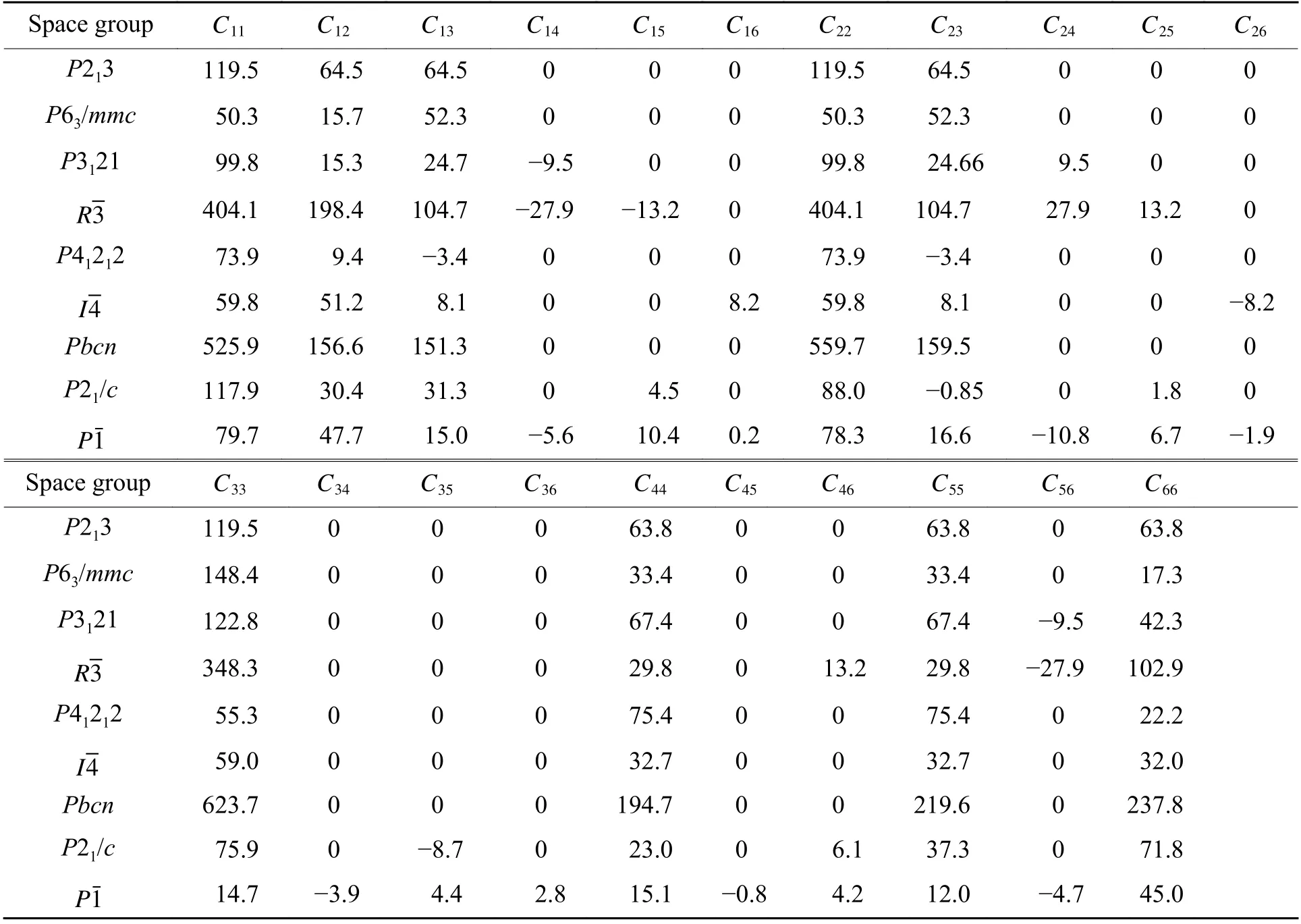
表2 计算得到的9 种SiO2 的弹性常数Table 2 Calculated elastic constants of nine kinds of SiO2 GPa

图1 9 种SiO2 的晶体结构（红色为氧原子，蓝色为硅原子）Fig. 1 Nine kinds of SiO2 crystal structures (The oxygen atom is red and the silicon atom is blue.)

根据第1 节中推导的7 大晶系的稳定性判据，讨论不同结构的SiO2晶体的力学稳定性。

(1) 空间群为P213（空间群序号：198）的立方相SiO2（β-方石英）的弹性常数满足式(1)，所以，其在0 GPa 下是力学稳定的。

(2) 空间群为P63/mmc（空间群序号：194）的六角相SiO2（β-磷石英）的弹性常数满足式(2)，所以，其在0 GPa 下是力学稳定的。Borisov 等[29]也认为此构型具有较高的稳定性。

(3) 空间群为P3121（空间群序号：152）的三角相SiO2（α-石英）的弹性常数满足式(3)，所以，其在0 GPa 下是力学稳定的。 研究表明，常温常压下，α-石英是最稳定的相[30-31]。

(4) 空间群为R3（空间群序号：148）的三角相SiO2的弹性常数满足式(4)，所以，其在0 GPa 下是力学稳定的。此相在高压下较稳定，在100 GPa 下声子无虚频[32]。

(5) 空间群为P41212（空间群序号：92）的四方相SiO2（α-方石英）的弹性常数满足式(5)，所以，其在0 GPa 下是力学稳定的。Coh 等[33]和Downs 等[34]认为此相具有局部稳定性（亚稳态）。

(6) 空间群为I4（空间群序号：82）的四方相SiO2（ZSM-11 型沸石）的弹性常数满足式(6)，所以，其在0 GPa 下是力学稳定的。Boisen 等[35]和Hochgräfe 等[36]认为此相在低温下是稳定的。

(7) 空间群为Pbcn（空间群序号：60）的正交相SiO2（赛石英，α-PbO2型）的弹性常数满足式(7)，所以，其在0 GPa 下是力学稳定的。此相虽然仅在高压环境中才会产生[37]，但已被证实其在常压下是较稳定的相[18]。

(8) 空间群为P21/c（空间群序号：14）的单斜相SiO2（斜锆石，α-ZrO2型）的弹性常数满足式(11)，所以，其在0 GPa 下是力学稳定的。Haines 等[15]发现斜锆石存在于自然界中，在其所处环境中是亚稳态。

(9) 空间群为P1¯（空间群序号：2）的三斜相SiO2（沸石）的弹性常数矩阵（单位：GPa）如式(13)所示，从式(12)可以看出，三斜相的力学稳定性判据极为复杂，相比之下，将具有确切数值的矩阵先经过初等变换转化为上三角矩阵，再判断其正定性会更容易。

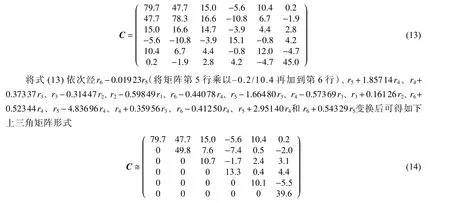
由初等变换的性质可知，式(13)经上述变换后，其值几乎保持不变，所以式(13)的值近乎等于式(14)的主对角线元素的乘积，故式(13)为正。同样地，式(13)的2、3、4、5 阶顺序主子式通过初等行变换也可以依次近似转化为上三角矩阵式(14)的2、3、4、5 阶顺序主子式形式，很明显，这4 个顺序主子式都为正，而且C11也为正，所以，三斜相SiO2在0 GPa 下是力学稳定的。

3 结 论

根据晶体的力学稳定性充要条件——弹性常数矩阵正定，推导了7 大晶系的Born 稳定性判据。特别地，补充了对称性较低的单斜和三斜晶系的力学稳定性判据，为稳定性判据在低对称性晶体结构中的应用提供了依据。采用基于DFT 框架下的广义梯度近似和超软赝势法，计算出了9 种SiO2的弹性常数，并根据稳定性判据对其稳定性进行了判定，结果显示9 种SiO2均为力学稳定。