Laplace-Stieltjes变换的广义型
张少吟,宁菊红*,黄文平
(1.江西师范大学数学与统计学院,江西 南昌 330022;2.陆军步兵学院基础部,江西 南昌 330103)
0 引言与预备知识
Laplace-Stieltjes(L-S)变换[1]
(1)
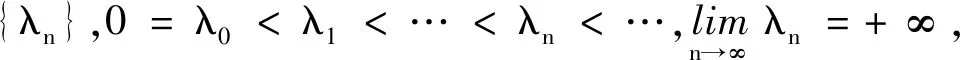
(2)
文献[2]研究得到:若L-S变换(1)满足条件
(3)
其中

类似于文献[2],引入F(s)的最大模Mu(σ,F)和最大项μ(σ,F)如下:
文献[2]还研究了最大模和最大项的关系,并得到如下结果.
引理1[2]若L-S变换(1)满足条件(2)和条件(3),则∀ε>0,当-σ充分大时,有
μ(σ,F)/2≤Mu(σ,F)≤μ(σ-D-ε,F).
为了研究L-S变换(1)所表示的整函数F(s)的增长性,类似于Dirichlet级数,定义其级如下.
定义1[3]L-S变换(1)所表示的整函数F(s)的级定义为
其中ln+x=max{lnx,0}.若0≤ρ<+∞,则称F(s)具有有限级;若ρ=+∞,则称F(s)具有无限级.
为了区分具有相同级ρ(0<ρ<+∞)的L-S变换的增长性,引入型的定义.
定义2[3]若ρ∈(0,+∞),则L-S变换(1)所表示的整函数F(s)的型定义为
关于L-S变换的增长性的研究,目前已得到一系列深刻的结果[3-15],这些文献分别研究了在全平面上解析的L-S变换所表示整函数的零级、有限级、无限级、型及其值分布.本文主要研究在全平面上解析的L-S变换所表示整函数的有限级及无限级的广义型.
1 有限级的广义型
本节主要研究具有有限级的L-S变换的广义型.
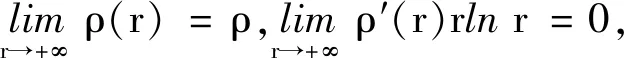
其中称U(r)=rρ(r)(r>0)为型函数,称ρ(r)为准确级,τ1是关于U(r)的型.
注1若定义3中的ρ(r)≡ρ,则型τ1≡τ,即此时广义型τ1为定义2的普通型τ.
引理2[7]令t=U(r),r=W(t)(r>0,t>0)互为反函数,则有
(i)U(kr)=(kρ+o(1))U(r)(r→+∞);
(ii)W(kt)=(k1/ρ+o(1))W(t)(t→+∞);
(iii)tW′(t)/W(t)=1/(ρ+o(1))(t→+∞).
引理3[3]若τ′和-σ是正数,则当-σ充分大时,函数X(λ)=λ((lnτ′eρ)/ρ-lnW(λ)-σ)有最大值
(1/ρ+o(1))U((τ′ρ)1/ρe-σ(1-o(1))).
引理4[3]若α和λ是正数,则当λ充分大时,函数φ(σ)=αU(e-σ)+λσ有最小值
λ/(ρ+o(1))-λln(W(λ)/(ρ1/ρα1/ρ+o(1))).
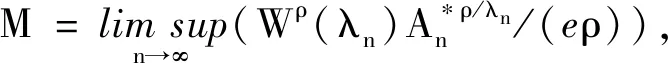
证先证τ1≤eρDM.若M=+∞,则显然成立.若0≤M<+∞,则由

由引理3知,当-σ充分大时,
lnMu(σ,F)≤lnμ(σ-D-ε,F)≤(1/ρ+o(1))ρ(M+ε)(1-o(1))ρeρ(D+ε)U(e-σ).
因此



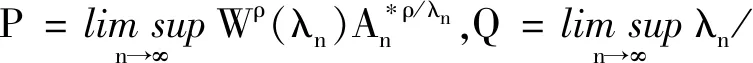
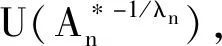
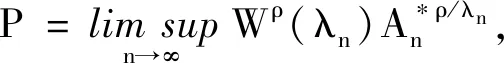
在一些特殊情况下,定理1和定理2有如下推论.
推论1若D=0,则在定理1的条件下有
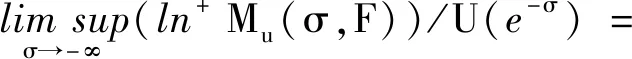
注2推论1是在文献[3]中的定理1.
推论2若ρ(r)≡ρ∈(0,∞),则在定理1的条件下有
进一步,若D=0,则显然有
注3推论2是在文献[5]中的定理2.
2 无限级的广义型
前面讨论了当F(s)为有限级时它的准确级的广义型,下面讨论当F(s)为无限级时它的准确级的广义型.为此,仿照定义3给出如下定义.
定义4L-S变换(1)所表示的整函数F(s)的p级定义为
其中ln0x=x,lnpx=ln(lnp-1x),称ρp为F(s)的p级.
本节主要研究p级对应的广义型,然后再返回一般的型.接下来类似给出p级对应的广义型的定义.

其中称U(r)=rρ(r)(r>0)为型函数,称ρ(r)为准确级,τp是关于U(r)的型.
注4显然当p=1时,级ρp就是在定义1中的级ρ,广义型τp就是在定义3中的广义型τ1.即定义1和定义3分别是定义4和定义5的特殊情况.当p=1时所对应的广义型τ1已经在第1节讨论,本节主要讨论当p=2,3,…时的广义型τp.

证先证Mp≤τp.若τp=+∞,则显然成立.若0≤τp<+∞,则由
知,∀ε>0,∃σ1<0,∀σ<σ1,有lnpMu(σ,F)≤(τp+ε)U(e-σ),则
Mu(σ,F)≤expp((τp+ε)U(e-σ)),
其中exp0(x)=x,exp1(x)=ex,exp2(x)=eex,…,expp(x)=expp-1ex.
由引理1知,若任意给定σ<σ1,对所有正整数n=1,2,…,有
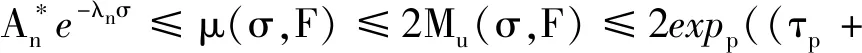
则
(4)

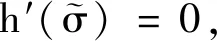
rU′(r)/U(r)=ρp(1+o(1))(r→∞),

对上式两端连续取p-1次对数,得
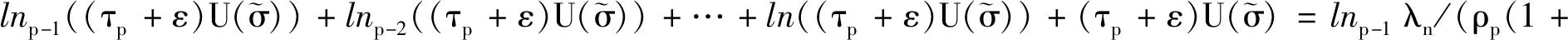
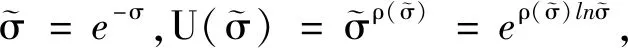

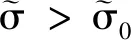
由式(4)和上式知
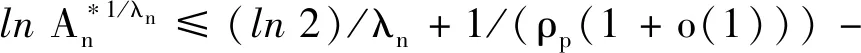

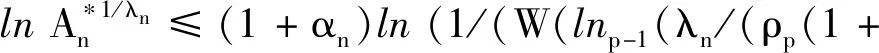
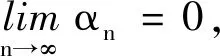
由ε的任意性知Mp≤τp.
接下来证τp≤MpeρpD.若Mp=+∞,则显然成立.若0≤Mp<+∞,则由Mp的定义知,∀ε>0,当n充分大时,有
任意取定σ<0,对每一个充分大的正整数n,有

g(x)=-xln(W(lnp-1x))+aσx,
aσ=(ln(Mp+ε))/ρp-σ,


g′(x)=-ln(W(lnp-1x))-lnp-1(xW′(lnp-1x)/
由引理2知,有
tW′(t)/W(t)=1/(ρp+o(1))(t→+∞),
又对充分大的x有
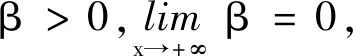
x0(σ)=expp-1U(eaσ-β).
又当x≥x0(σ)时,g′(x)≤0;当x≤x0(σ)时,g′(x)≥0.因此g(x)在x=x0(σ)处取最大值且有
βexpp-1U(eaσ-β).
(5)
由引理1和式(5)有
(lnpMu(σ,F))/U(e-σ)≤(lnpμ(σ-D-ε,F))/U(e-σ)≤U(e(ln(Mp+ε))/ρp-σ+D+ε-β)/U(e-σ).
再由引理2和ε的任意性得
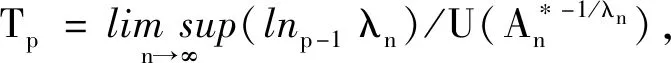
证此定理证明类似于定理2.
在一些特殊情况下,由定理3和定理4可类似得到如下推论.
推论3若D=0,则在定理3和定理4的条件下有
推论4若ρ(r)≡ρp,则在定理3的条件下有
进一步,若D=0,则有
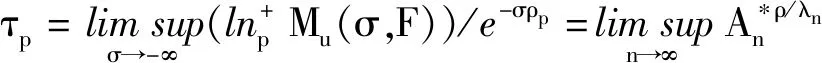
注5从几个定理及推论可以看到,τp在p=1时的表示式和在p=2,3,…时的表示式相差常数eρ.

