概率对偶犹豫模糊PROMETHEE多属性群决策算法

朱钰婷，张文宇，2，侯俊杰，张仁杰

1.中国航天系统科学与工程研究院，北京 100048

2.西安邮电大学 经济与管理学院，西安 710061

随着参与决策人数的增加，决策过程变得更复杂，因而多属性群决策（multi-attribute group decision making，MAGDM）在现代决策理论和决策科学中发展为一个极为重要的研究领域，在工程、物流、医学及军事等诸多方面都有着广泛的应用。1965 年，Zadeh[1]提出模糊集（fuzzy sets，FSs）理论以来，这一理论常用于处理实际生活中具有模糊性和不确定性的问题。Atanassov[2]定义了直觉模糊集（intuitionistic fuzzy sets，IFSs），该模糊集认为隶属度与非隶属度之和应小于等于1[3]。Yager[4]提出的毕达哥拉斯模糊集（pythagorean fuzzy sets，PFSs），将隶属度和非隶属度范围扩大至平方和小于等于1[5]。考虑到决策者在决策过程中可能会对隶属度值存在犹豫的现象，Torra[6]提出了犹豫模糊集（Hesitant fuzzy sets，HFSs）。近年来，国内外学者对犹豫模糊集[7-8]进行了较为广泛的研究，Zhu 等[9]通过定义可能隶属度与可能非隶属度提出对偶犹豫模糊集（dual hesitant fuzzy sets，DHFSs）。Xu 等[10]在犹豫模糊集的基础上提出了概率犹豫模糊集（probabilistic hesitant fuzzy sets，PHFSs），不仅提供了每个评价方案的所有隶属度，并且提供了各个隶属度对应的概率。Hao 等[11]在概率犹豫模糊集和对偶犹豫模糊集的基础上定义了概率对偶犹豫模糊集（probabilistic dual hesitant fuzzy sets，PDHFSs），该模糊集既能够从隶属度与非隶属度角度收集决策信息，又包含了对应的概率信息[12]。与PHFSs、DHFSs等犹豫模糊集相比，概率对偶犹豫模糊集对决策者的犹豫不决与心理偏好表达得更加准确，减少了决策过程中评价信息缺失的情况，PDHFSs作为2017年提出的理论，相关的理论研究及实际应用亟需丰富。

Brans 等[13]提出的偏好顺序结构评估法（preference ranking organization method for enrichment evaluations，PROMETHEE），是一种建立在“级别高于关系”的多准则决策方法。相比常用的信息集结算子，如加权平均算子[14]、加权几何平均算子[15]等，PROMETHEE 方法思路清晰、简单有效，对环境具有灵活性和适应性，能够保证方案决策结果的稳定性与可靠性，已经成功地运用于各种领域，例如医疗服务[16]、舆情管控方案评选[17]、FMEA风险评估[18]、水资源方案评估[19]等研究。

多属性群决策问题考虑的是个人视角很难完成的决策，需要从多视角去做出判断的问题。因此，多属性群决策算法的研究对现代决策的发展十分必要，尤其是模糊信息和犹豫决策这两个方面已经成为学术界的重要研究领域。目前尚未发现有研究基于概率对偶犹豫模糊集与PROMETHEE 扩展的模糊信息评价算法，并用来解决多属性群决策问题。综上，本文提出一种基于概率对偶犹豫模糊集与PROMETHEE结合的多属性决策算法（以下简称PDHFSs-PROMETHEE）。该算法首先通过概率对偶犹豫模糊语言描述决策信息，根据改进的得分函数和偏差函数集成概率对偶犹豫模糊元素，解决了决策信息难以定量化表达的问题；其次通过PDHFWA算子将各决策者的决策信息聚合为概率对偶犹豫模糊综合评价矩阵；最后通过PROMETHEE 方法判断航空灾难事故应急响应备选方案的优先级，得到最优决策方案。

1 基本概念

1.1 概率对偶犹豫模糊集

如果S(pd1)＜S(pd2)，则pd1＜pd2；

如果S(pd1)=S(pd2)，则：

（1）如果σ(pd1)＜σ(pd2)，则认为pd1优于pd2，记为pd1＞pd2。

（2）如果σ(pd1)=σ(pd2) ，则认为pd1与pd2无差别，记为pd1～pd2。

定义5 概率对偶犹豫模糊元素的偏离度能够反映所有信息的稳定性，为了在得分函数中能够充分考虑概率对偶犹豫模糊元素的偏离度，对概率对偶犹豫模糊元素的得分函数提出改进。改进的得分函数不仅克服了原始得分函数的两步计算法与忽略偏离度的问题，只需要一步计算即可得到信息比较的结果，并且考虑了犹豫信息对隶属度与非隶属度不同的影响，使信息比较结果更加具有可靠性。

设pd=h͂,g͂=h|p,g|q为一个概率对偶犹豫模糊元素，改进的概率对偶犹豫模糊元素的得分函数表示为：

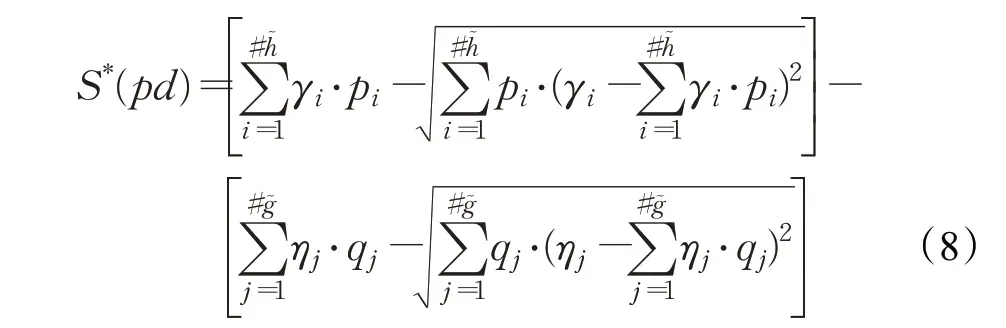
其中，γi∈h、pi∈p分别表示隶属度部分的隶属度值与相应的概率，ηj∈g、qj∈q分别表示非隶属度部分的非隶属度值与相应的概率。#h͂(x)和#g͂(x)分别表示隶属度和非隶属度中相应元素的个数。

定义6 基于定义5中改进的得分函数，两个概率对偶犹豫模糊元素pd1和pd2之间的比较可以表示为：

（1）如果S*(pd1)＞S*(pd2)，则认为pd1优于pd2，记为pd1＞pd2。

（2）如果S*(pd1)＜S*(pd2)，则pd1＜pd2。

（3）如果S*(pd1)=S*(pd2)，则说明pd1与pd2无法区分，记为pd1～pd2。

概率对偶犹豫模糊加权平均算子（PDHFWA）的集成结果是概率对偶犹豫模糊元，且满足下列优良性质：

（1）置换不变性：令αi=ωi pdi，设(β1,β2,…,βn)是(α1,α2,…,αn)的任一置换，则PDHFWA(α1,α2,…,αn)=PDHFWA(β1,β2,…,βn)。

（2）有界性：设αi=ωih͂i(x),ωig͂i(x) (i=1,2,…,n)为一组加权概率对偶犹豫模糊数，αmin≤PDHFWA(α1,α2,…,αn)≤αmax。

（3）单调性：设α′i=ωih͂′i(x),ωig͂′i(x) (i=1,2,…,n)为另一组PDHFWA，若αi≤α′i，则PDHFWA(α1,α2,…,αn)≤PDHFWA(α′1,α′2,…,α′n)。

（4）幂等性：令pdi=＜h͂i(x),g͂i(x)＞(i=1,2,…,n)为一组PDHF，如果对于所有的i=1,2,…,n，都有hi=h={γ}，gi=g={η}，pd1=pd2=…=pdn=pd，可得：

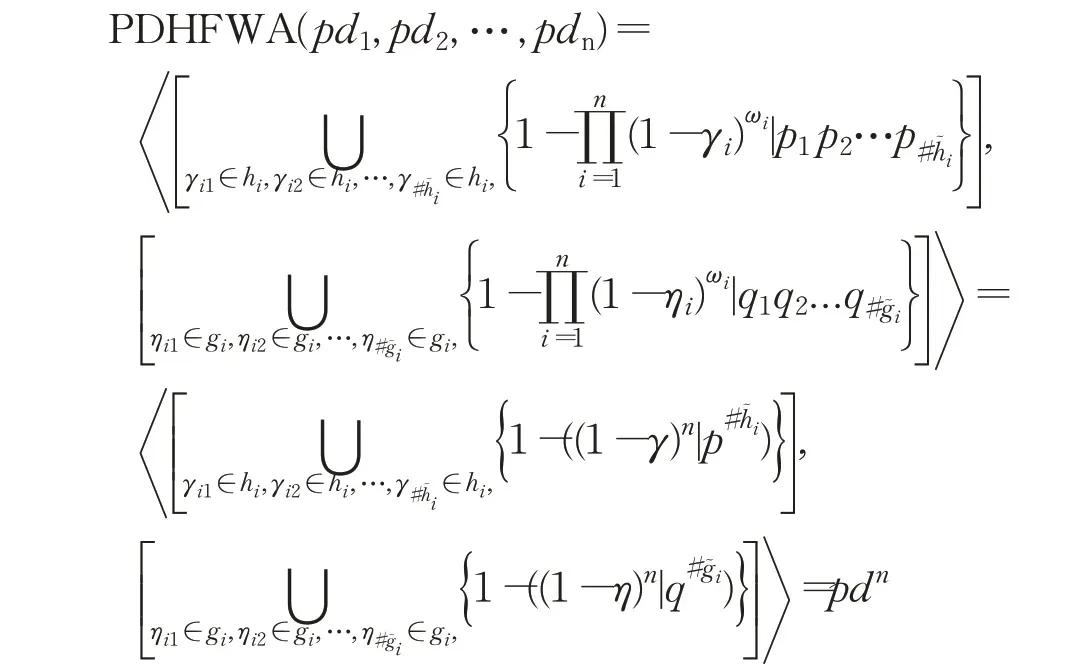
1.2 PROMETHEE方法

PROMETHEE 方法通过引入优先函数来描述在同一属性Cj上关于决策的优先程度，即根据各决策属性值之间差距的大小来判断决策对之间的优劣程度[22]。

PROMETHEE 方法中有6 种形式的偏好函数[23]，具体如下所示。

（1）一般准则为：

（5）线性无差别区间准则为：

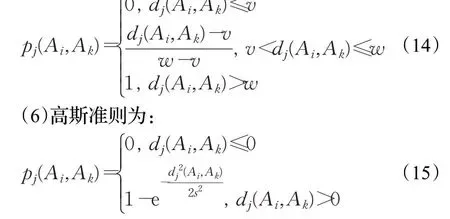
无论选择哪种偏好函数，都应计算dj(Ai,Ak)=f(Ai)-f(Ak)，其表征任何两种备选方案之间的偏好差异。因此，PROMETHEE方法对每一个指标定义一个优先函数，函数值值域为0～1，函数值越小，方案Ai和Ak之间的差异越小；当函数值为0 时，方案Ai和Ak无差异；其值越接近1，方案Ai优于方案Ak的程度就越高；而当函数值为1时，方案Ai严格优于方案Ak。

2 基于概率对偶犹豫模糊PROMETHEE的多属性群决策算法

本章主要介绍了PDHFSs-PROMETHEE 多属性群决策算法的步骤。首先得到各位决策专家为相关决策问题提供的评价信息；其次，利用概率对偶犹豫模糊集理论的相关知识将其集结成综合决策信息矩阵；最后通过PROMETHEE 方法计算各个决策方案的流出值、流入值和净流值，并根据各对决策的净流值大小，确定决策间的级别关系从而得到决策结果。

PDHFSs-PROMETHEE 多属性群决策算法对应的流程图如图1所示。

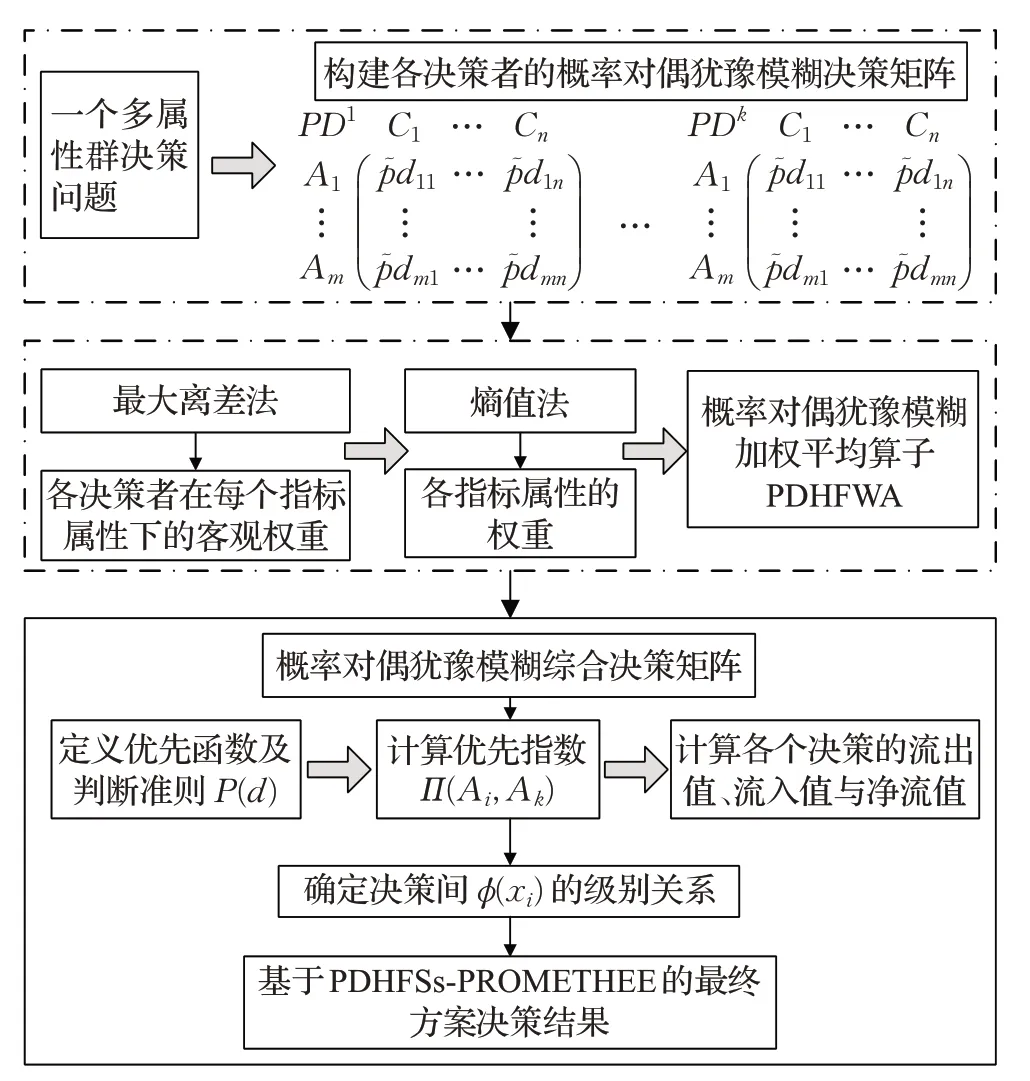
图1 PDHFSs-PROMETHEE多属性群决策算法流程图Fig.1 PDHFSs-PROMETHEE multi-attribute group decision-making method solution flow chart

基于PDHFSs-PROMETHEE 多属性群决策算法的具体步骤如下：

步骤1 构建概率对偶犹豫模糊决策信息矩阵。

其中，1 ≤i≤m,1 ≤j≤n,1 ≤j*≤n。

步骤3 用熵值法计算指标属性C={Cj}的权重。

信息熵是对系统无序程度的度量，采用熵值法确定指标的变异程度及指标水平的综合测度，可以有效避免人工确定指标权重的主观性[25]。在指标矩阵X中，指标的熵值越大，表明该项指标的变异程度越大。熵值法计算的步骤如下：

（1）用功效系数法对决策方案的指标数据矩阵X进行标准化处理。

步骤4 计算综合决策评价矩阵。

（1）根据定义7 中的PDHFWA 算子，计算出各专家在每个方案下根据各指标的综合评价值。

在具体的多属性决策问题中，选定线性的优先函数，可以得到pj(AI,AK) 的值，进而求得Π(AI,AK)的值。

3 算例

3.1 算例分析

近年来航空灾难事故频发，为降低航空灾难事故造成的人员伤亡和财产损失，某应急管理机构拟在几个备选方案中选择一个有效的应急响应方案[26]。经调查研究，现有4个应急响应方案（A1,A2,A3,A4）进入最终的评估范围，备选方案的评估准则（指标属性）为：指挥能力（C1）、救援能力（C2）、响应能力（C3）、预测能力（C4）。依托4 位行业经验丰富的专家、高级官员（E1,E2,E3,E4）为应急响应方案评估提供智力支持。本节采用PDHFSs-PROMETHEE 多属性群决策算法对备选应急响应方案进行评估，具体求解步骤及结果如下：

步骤1 各位决策专家Ek根据指标属性Cj对4 个应急响应方案Ai给出评价信息，得到模糊决策信息矩阵PD(k)(k=1,2,3,4)，表1～4 分别表示各决策专家的概率对偶犹豫模糊评价决策矩阵。

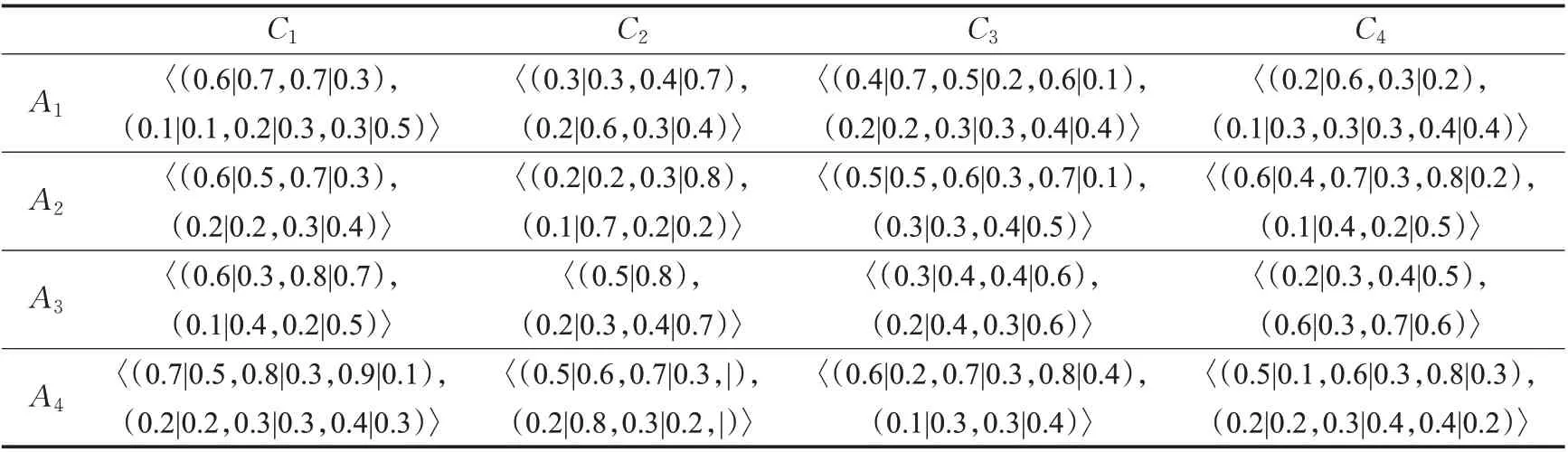
表1 决策专家E1 给出的评价值决策矩阵Table 1 Evaluation value decision matrix given by decision expert E1

步骤2 基于最大离差法，确定4位决策专家分别在每个指标属性下的客观权重，如表5所示。

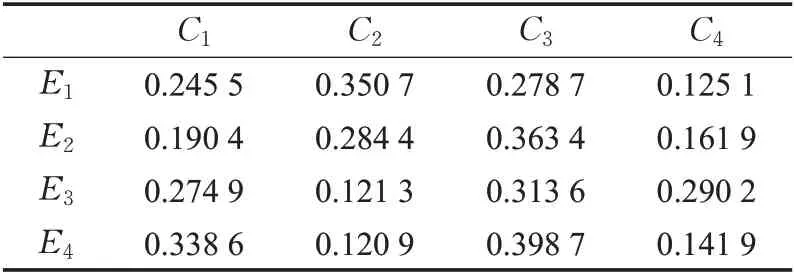
表5 各决策专家在不同指标属性下的客观权重Table 5 Objective weights of decision-making experts on different index attributes

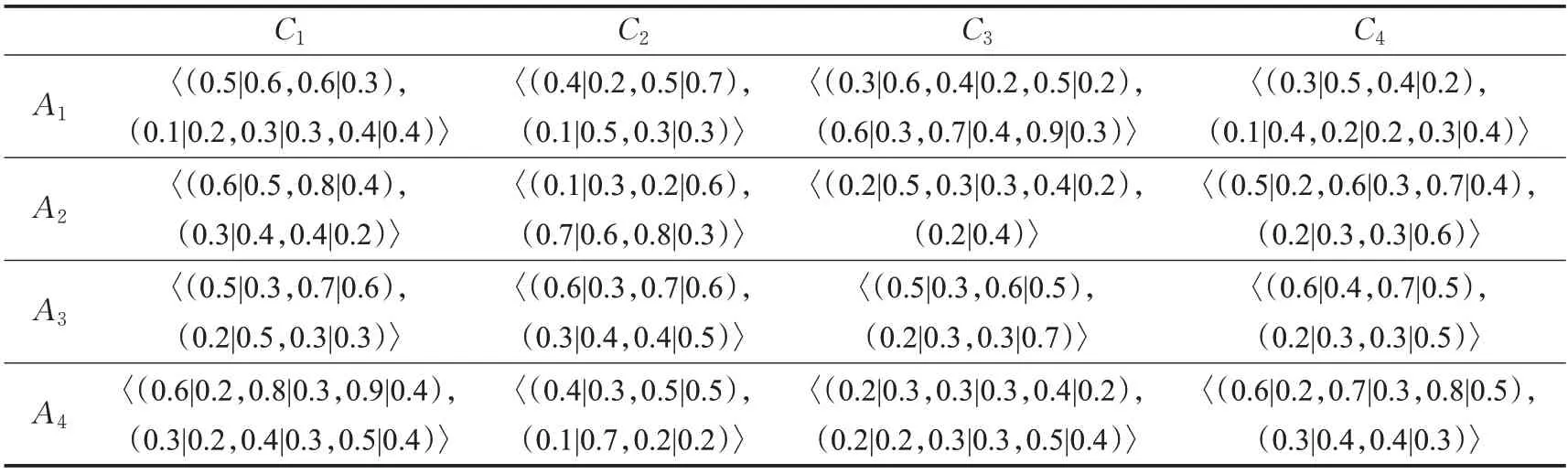
表2 决策专家E2 给出的评价值决策矩阵Table 2 Evaluation value decision matrix given by decision expert E2

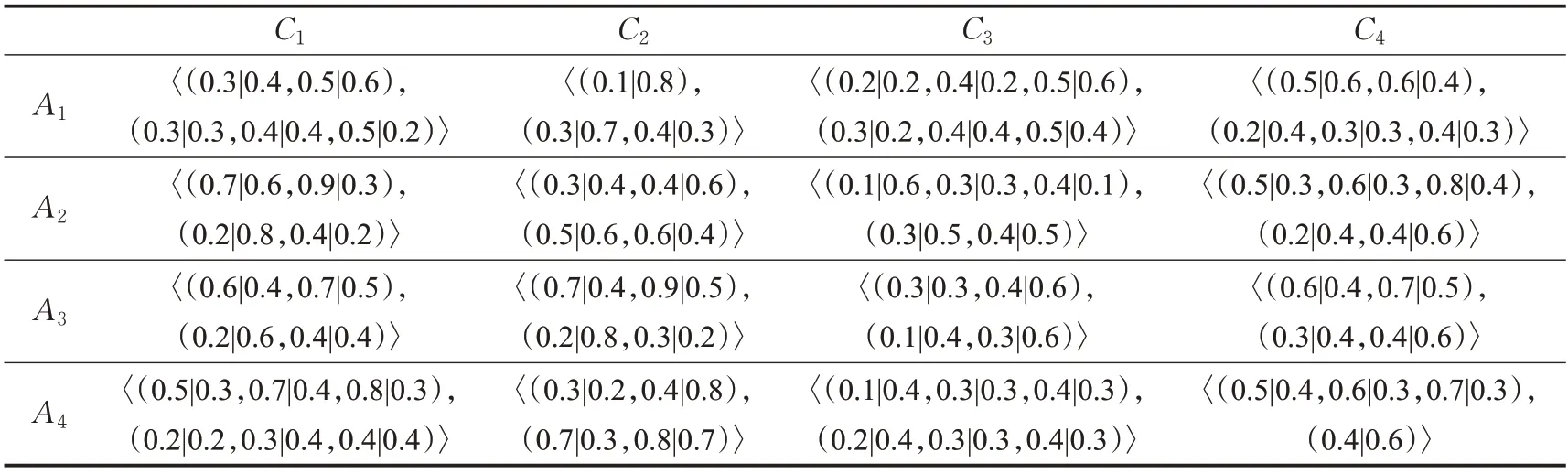
表3 决策专家E3 给出的评价值决策矩阵Table 3 Evaluation value decision matrix given by decision expert E3

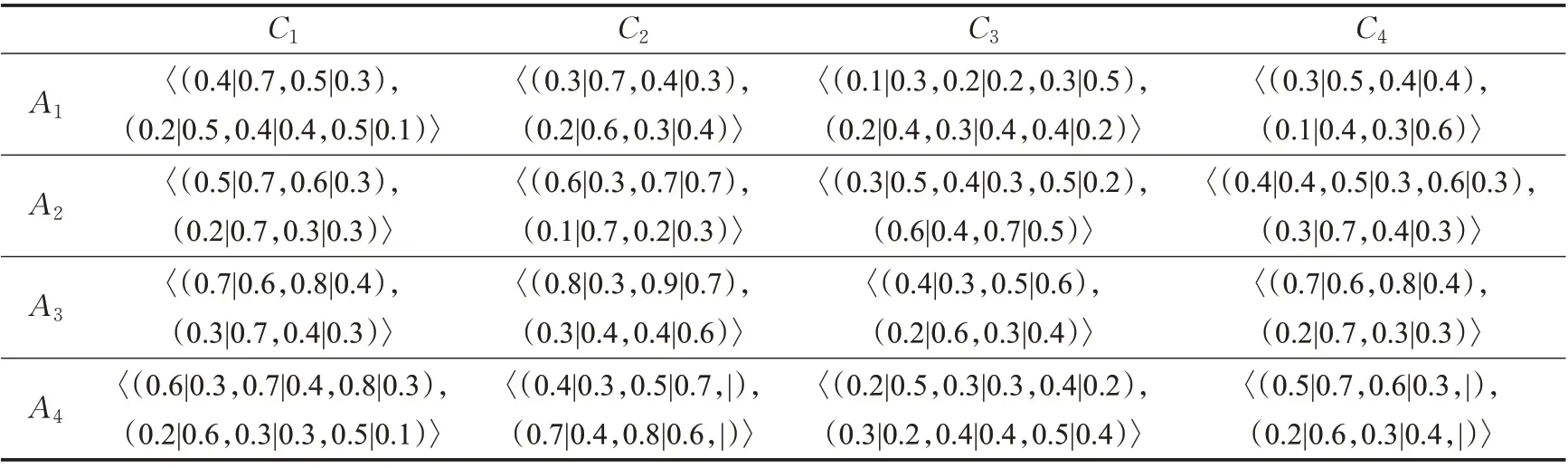
表4 决策专家E4 给出的评价值决策矩阵Table 4 Evaluation value decision matrix is given by decision expert E4

步骤3 基于熵值法，确定指标属性C={Cj}的权重wj，计算结果如表6所示。

表6 各指标属性的权重Table 6 Weights of each indicator attribute

步骤4 根据权重与PDHFWA 算子，得到各决策专家的综合决策评价矩阵，如表7所示。

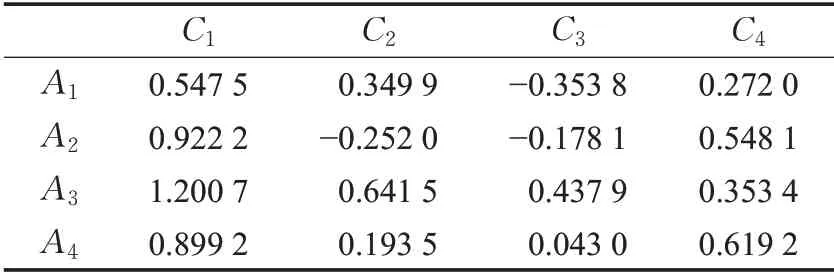
表7 各决策专家的综合决策评价矩阵Table 7 Comprehensive decision-making evaluation matrix of each decision-making expert

步骤5 计算优先指数。选择具有线性优先关系准则确定优先函数，按照式（23）计算每一对方案Ai,Ak∈A的优先指数Π(Ai,Ak)，结果如表8所示。

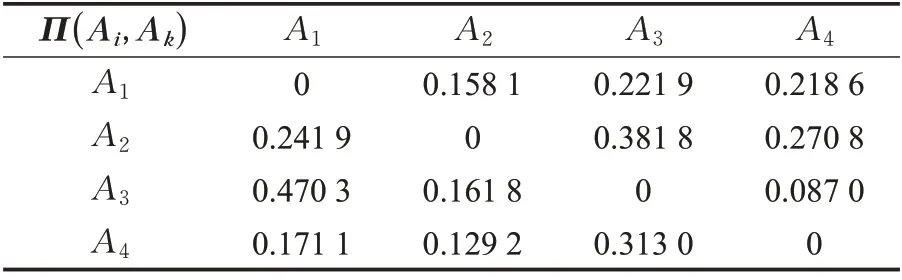
表8 优先指数Π( Ai,Ak)Table 8 Priority index Π( Ai,Ak)

步骤6 按照式（24）、（25）与式（26）计算每个应急响应方案的流出、流入和净流值，计算结果如表9所示。

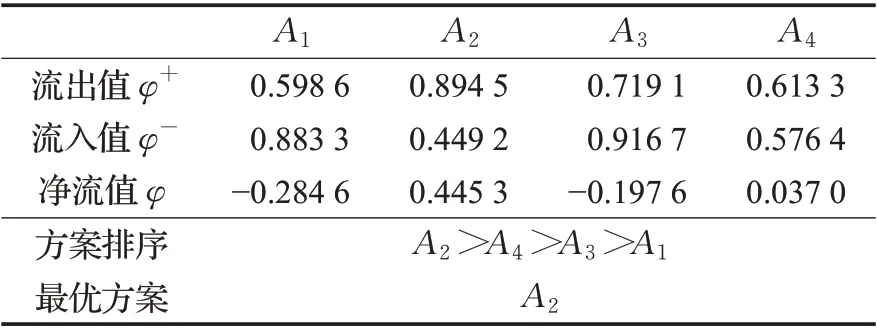
表9 各方案的流出值φ+、流入值φ-和净流值φTable 9 Outflow value φ+，inflow value φand net flow value φ of each scheme

步骤7 通过计算决策集A上各对决策的流出值、流入值与净流值，净流值计算结果越大，方案越优。

故基于本文提出的PDHFSs-PROMETHEE 多属性群决策算法，4 个备选应急响应方案的排序为A2＞A4＞A3＞A1，可以确定最优应急响应方案为A2。

3.2 算法对比

在接下来的部分，对本文提出的算法与现有的多属性决策算法进行比较。在已有的研究中，王应明等[27]提出了基于前景理论的TOPSIS 决策算法，应用于评估创新型企业的问题；陈秀明等[28]提出改进的VIKOR 决策算法，对电影推荐项目进行排序；Hao 等[11]提出应用PDHFS 决策算法，对北极地缘政治风险进行评估。本节将以上3种多属性决策算法应用于本文3.1节提出的航空灾难事故应急响应方案评估算例，本文算法与3种多属性决策算法的比较如表10所示。

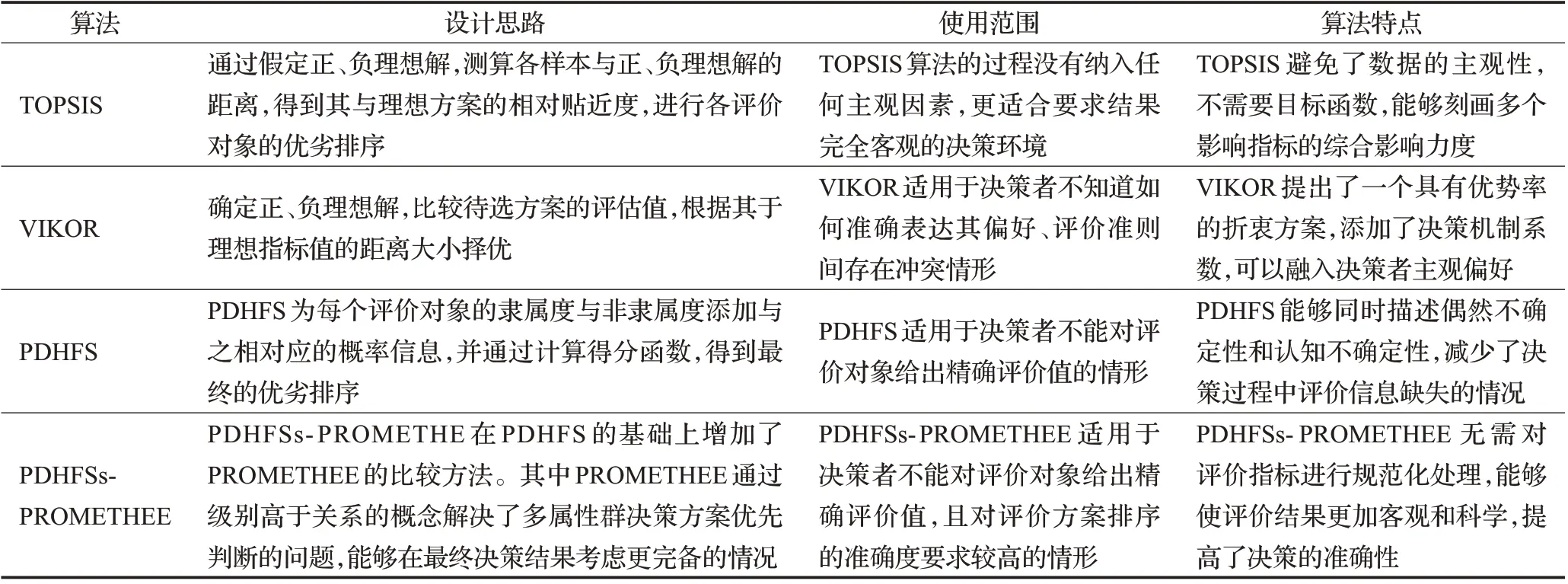
表10 4种多属性群决策算法比较Table 10 Comparison of four multi-attribute group decision algorithms

为了增强算法的可对比性，专家的重要程度与指标属性的权重向量值与本文3.1节中的计算结果一致，3种决策算法的计算过程如下：

（1）TOPSIS决策算法

通过文献[27]所提TOPSIS 决策算法，计算可得各应急响应方案Ai分别到正理想解和负理想解的犹豫模糊欧几里得距离集，如表11和表12所示。

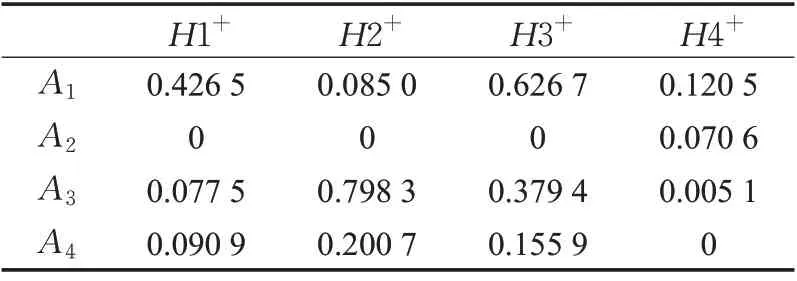
表11各方案到正理想解的距离集Table 11 Set of distances from each scheme to positive ideal solution

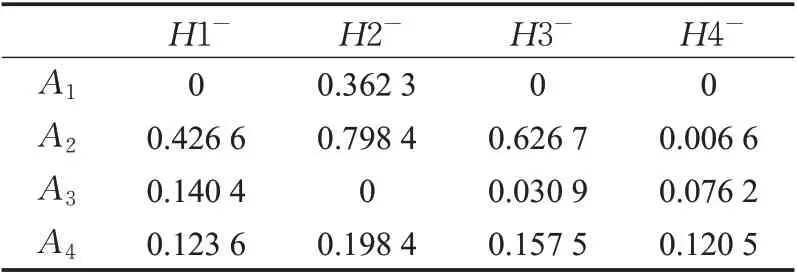
表12 各方案到负理想解的距离集Table 12 Set of distances from each scheme to negative ideal solution

通过计算可得各应急响应方案Ai的收益损失比值Ci，如表13所示。

表13 收益损失比值Table 13 Profit loss ratio

最后按照Ci值的大小对各方案进行排序，计算出的Ci值越大，方案越优。故基于前景理论TOPSIS决策法得应急响应方案的排序为A3＞A2＞A4＞A1，方案A3为最优应急响应方案。

（2）VIKOR决策算法

通过文献[28]所提VIKOR决策算法，计算可得各应急响应方案Ai的正理想点m+和负理想点m-，正负理想点的具体值见表14。

表14 各方案群体偏好的理想点Table 14 Ideal point of preference for each program group

设决策机制系数为0.5 时，通过计算可得群体效用变量MU，个体遗憾变量MR与妥协解变量MC，计算结果如表15所示。

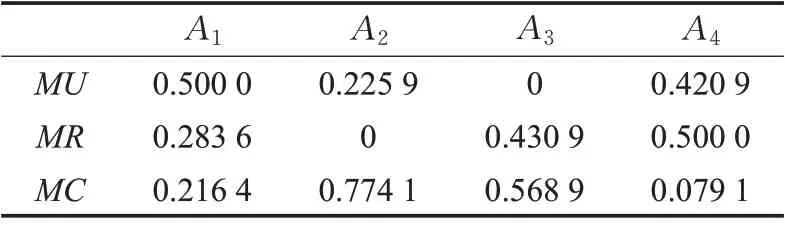
表15 模糊语言信息的MU、MR与MC值Table 15 MU，MR and MC values of fuzzy linguistic information

最后按照群体效用变量MC值的大小对方案进行排序，方案的MC值越大，则判断方案越优。故基于改进的VIKOR 决策算法得到应急响应方案的排序为A2＞A3＞A1＞A4，方案A2为最优应急响应方案。

（3）PDHFS决策法

通过文献[11]所提PDHFS决策算法，计算概率对偶犹豫模糊信息原始得分函数可得各应急响应方案Ai的得分值，结果如表16所示。

表16 4个应急响应方案的得分值Table 16 Scores for four emergency response options

最后按照得分值的大小对方案进行排序，计算出的得分值越大，方案越优。故基于PDHFS 决策算法得到方案的排序为A2＞A4＞A3=A1，方案A2为最优应急响应方案。

3.3 结果分析

本文基于TOPSIS、VIKOR、PDHFS 与PDHFSs-PROMETHEE 这4 种决策算法对航空灾难事故应急响应方案的决策评估结果如表17所示，4种决策算法中各备选方案的效用值分布趋势如图2所示。

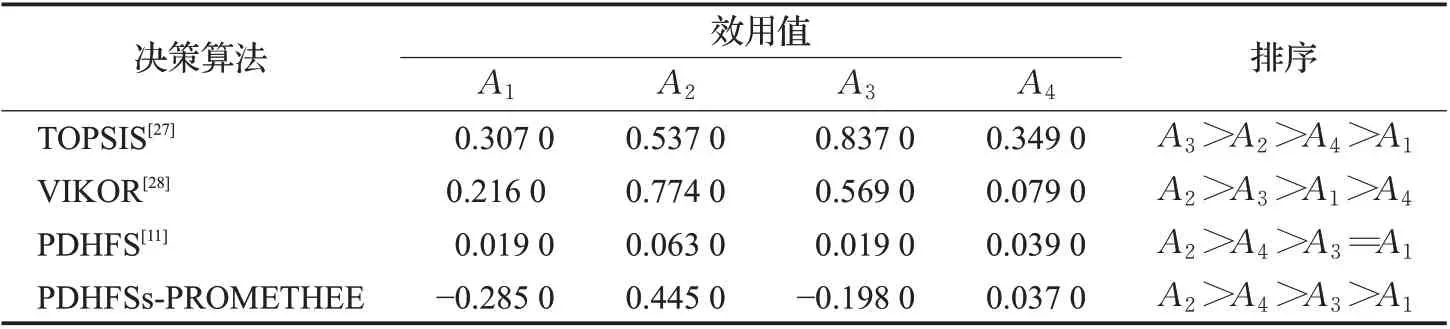
表17 4种算法的决策评估结果Table 17 Decision evaluation results of four methods

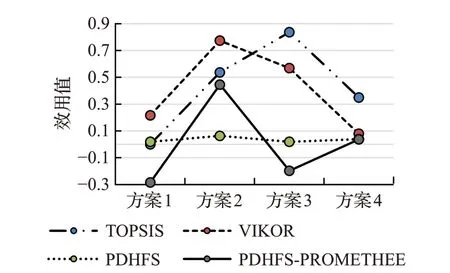
图2 4种算法下各备选方案的效用值分布趋势图Fig.2 Utility value distribution trend diagram of each alternative under four methods

由计算结果可见，TOPSIS 决策算法判断A3优于A2，可能因为忽略了方案A3在C2指标属性下评价不佳。VIKOR 决策算法判断方案A3优于A4，可能由于折衷理论在计算最终效用值上具有局限性。PDHFS决策算法在模糊信息元素比较中忽略了偏离函数的影响，最终无法判断方案A1与A3的优先等级。此外，应急响应方案A1在TOPSIS、PDHFS与PDHFSs-PROMETHEE这3种决策算法的排序中排名均处于最后一位，应急响应方案A2在VIKOR、PDHFS与PDHFSs-PROMETHEE这3种决策算法的排序中排名均处于第一位，说明最终决策结果的有效性。不同决策算法中的具体排名略有不同，是由于决策算法各自的特性及侧重点差异所导致的。本文提出的PDHFSs-PROMETHEE 算法在进行决策的过程中，对于不同的指标属性赋权，得到的决策结果不完全一样，这与实际情况相符。该算法充分考虑决策者对属性的偏好情况，且计算结果区分度大、直观性强，决策结果更具有说服力[29-31]。每个备选的航空灾难事故应急响应方案都有自己的优势，各指标属性权重可以根据不同城市与航空灾难事故的等级，对应急响应效果确定具体需求，从而评估得到最优的应急响应方案。

由以上结果可以看出，本文应用的PDHFSs-PROMETHEE 多属性群决策算法具有可行性，能够决策出最佳的应急响应方案。与现有研究中的决策算法相比，本文采用的决策算法提出将概率对偶犹豫模糊集与PROMETHEE方法相结合，在概率对偶犹豫模糊元素信息比较中同步考虑了得分函数与偏离函数的计算，并通过PROMETHEE方法判断决策方案的优先级。该算法能够解决多个不同类型的多属性信息问题，得到准确的决策评价结果，具有可靠性与有效性。

4 结束语

研究基于概率对偶犹豫模糊集与PROMETHEE 结合的多属性决策算法及其应用。主要工作体现在三个方面：（1）提出了将PROMETHEE方法拓展至概率对偶犹豫模糊集的概念；（2）研究了基于概率对偶犹豫模糊PROMETHEE的多属性群决策算法，包括提出改进的得分函数，PDHFWA聚合算子与权重确定等方法，为犹豫模糊信息领域提供了一类新的研究途径；（3）通过评估航空灾难事故应急响应方案，验证了本文所提PDHFSs-PROMETHEE多属性群决策算法的有效性，并与现有的几种决策算法进行了对比，证明了决策结果的可靠性。本文提出的概率对偶犹豫模糊PROMETHEE多属性群决策算法可以应用到应急决策、物流管理、风险评估等诸多领域，是对犹豫模糊多属性群决策研究领域的丰富与拓展。今后，将结合更多的实际问题拓展概率对偶犹豫模糊PROMETHEE多属性群决策算法的应用研究。