面向机械臂轨迹规划的强化学习奖励函数设计

靳栋银，李 跃，邵振洲，施智平，关 永，4

1.首都师范大学 信息工程学院，北京 100048

2.首都师范大学 轻型工业机械臂与安全验证北京市重点实验室，北京 100048

3.河北工业职业技术学院 计算机技术系，石家庄 050000

4.首都师范大学 成像技术北京市高精尖创新中心，北京 100048

现如今，随着信息化和工业化的不断融合，机器人技术飞速发展，机器人已经被广泛应用在多个领域，比如军事、航天、医疗服务、资源勘探开发和家庭娱乐等[1-3]。作为机器人控制的关键技术之一[4-5]，轨迹规划旨在计划机器人从起点到目标点并避开障碍物的路线。由于机器人经常工作在复杂并具有非结构化特点的环境下，因此，特别需要机器人具有良好的轨迹规划能力以应对多变的工作环境[6-7]。随着机器人工作环境的非结构化程度不断加深，机器人智能化要求不断提高，更加迫切需要机器人可以很好地自主规划轨迹。

多年来，许多研究者已经提出了不同的轨迹规划方法，而且这些方法已经不同程度地应用到了机器人领域。Piazzi等人[8]提出了全局最小加加速度的轨迹规划方法，该方法所规划的轨迹与人类关节运动具有理想的相似性。Liu等人[9]基于动力学方程建立目标函数，从而使机器人以最小的成本沿着指定的几何路径移动。Saramago 等人[10]提出了一种基于有障碍环境的最佳运动轨迹方法，该方法考虑了机器人非线性动力学、执行器约束、关节限制和避障等因素。但这些轨迹规划方法都是在已知的工作环境下实现的，无法应用于未知的环境，如何提高机器人对工作环境的适应性成为了轨迹规划研究的一个难点[11-13]。

随着深度强化学习方法的不断成熟，研究人员利用其强大的学习能力，开始将深度强化学习与机器人轨迹规划任务相结合，并相继提出了各种深度学习强化方法，例如DQN[14]、DoubleDQN[15]、DuelingDQN[16]、Rainbow[17]等。但是早期的深度强化学习方法大多基于离散的动作空间，无法应用到类似机械臂轨迹规划这类连续动作空间的任务上。为此，Lillicrap 等人[18]提出了深度确定性策略梯度（deep deterministic policy gradient，DDPG）算法，该算法可以学习高维、连续动作空间的策略，使深度强化学习方法成功应用到机械臂轨迹规划任务中。但是由于训练成本比较大并且只能利用历史策略采集而来的数据进行策略更新，Mnih 等人[19]创新性地通过异步梯度下降法更新参数，提出了异步的优势行动者评论家算法（asynchronous advantage actor-critic，A3C）。A3C 使用多线程并行计算，在强化学习的训练过程中，并行地训练多个智能体，这样智能体可以在同一时间收集到不同的状态。与强化学习中的经验回放技术相比，这种方法不仅占用更小的内存，交互时间较短，而且对硬件的依赖性较低。

虽然以上的深度强化学习方法应用到了轨迹规划任务中，但是学习速度慢，时间就会变长，学习速率快又容易引起躁动。为了限制更新步长，2017 年，Heess 等人[20]提出了基于分布式近端策略优化（distributed proximal policy optimization，DPPO）的深度强化学习方法。该方法采取惩罚机制，为智能体提供更合理的学习步长。但是DPPO 的奖励函数只考虑了最终的规划结果是否成功，没有对轨迹规划的中间过程设计相应的奖励值，导致这种方式在探索阶段具有一定的盲目性，存在大量的无效探索。

为了解决上述问题，本文设计了一种基于语音的奖励函数，降低轨迹规划过程中的盲目性，为基于深度强化学习的机器人轨迹规划提供参考。在具体实施时，针对轨迹规划任务设计了相应的语音指令。在任务执行前预先由操作员发布这些特定指令，并基于马尔科夫链对操作员的语音指令进行建模，然后设计相应的语音奖励函数，最后将语音奖励函数与DPPO深度强化学习方法相结合，为机械臂轨迹规划提供全局指导信息，增强机械臂学习的方向性，从而有效地提升机械臂轨迹规划的收敛速度。本文所设计的语音奖励函数可以利用语音指导机械臂的轨迹规划，准确判断机械臂所规划的轨迹和语音指令的契合程度，从而提升机械臂轨迹规划的性能。

1 语音奖励函数设计

机械臂通常工作在复杂的环境中，其中，环境包含障碍物是比较典型的一种。而这种情况下理想避障轨迹的四条指令是：“靠近障碍物”“避开障碍物”“靠近目标点”和“到达目标点”。

马尔科夫链描述的是一种状态序列，序列中的每一个状态都是根据前面的有限个状态得到的。利用马尔科夫链进行建模时，某一状态可以有两种变化，转变到另一个不同状态，或者保持当前状态不变[21]。

由于马尔科夫链的原理与机械臂避障轨迹的四条指令吻合度较高，因此，本文将两者结合起来，基于马尔科夫链对这四条语音指令进行奖励函数建模，如图1所示。当机械臂的工作环境存在障碍物时，障碍物所处的位置对于机械臂的工作是至关重要的。当障碍物位于机械臂和目标中间时，则是障碍物位置影响轨迹规划任务较大的典型情况。

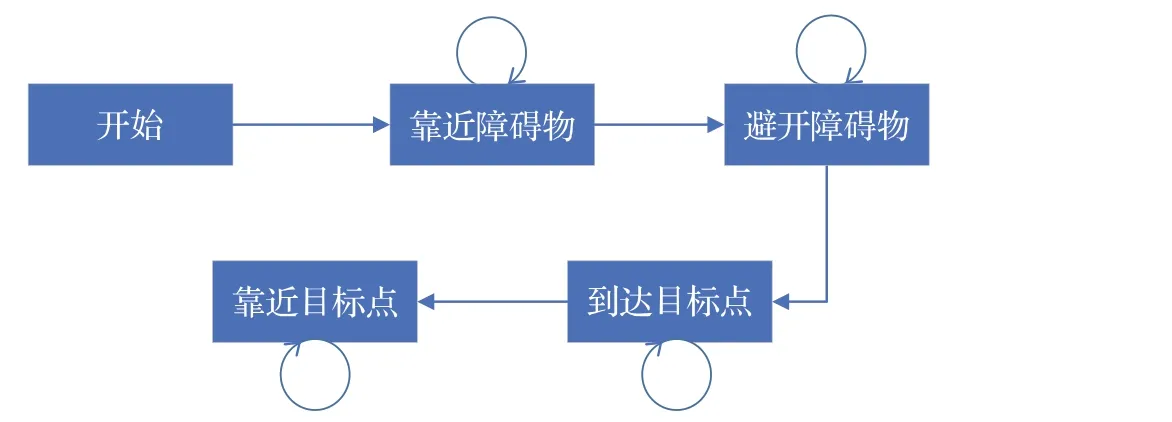
图1 基于马尔科夫链的语音指令模型图Fig.1 Voice command model diagram based on Markov chain

本文基于这种典型的情况设计奖励函数。在这种情况下，首先机械臂处于靠近障碍物的状态，机械臂的运行轨迹要保证不触碰到障碍物的情况下靠近障碍物；然后，机械臂接近障碍物到一定程度时状态发生转移，机械臂状态从靠近障碍物转变为避开障碍物，此时机械臂需要通过在障碍物两侧做弧线轨迹实现原先轨迹的偏离；接着，当机械臂绕开障碍物以后，状态会再次发生转移，由避开障碍物状态转变为靠近目标点状态；最后，机械臂完全到达目标点时，状态会从靠近目标点跳转成至到达目标点，到此完成了轨迹规划任务。本文基于马尔科夫链模型，将机械臂同障碍物和目标点的相对距离作为重要参数，设计了基于语音的奖励函数。

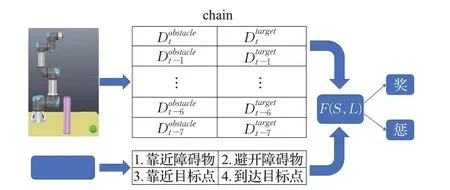
图2 奖励函数示意图Fig.2 Diagram of reward function

（1）靠近障碍物

当机械臂处于“靠近障碍物”状态时，需要综合考虑两个关键因素。其中一个关键因素是机械臂的轨迹要不断靠近障碍物，如公式（1）所示：

其中Dsafety表示机械臂的安全距离，当机械臂的运行轨迹满足公式（2）时，则可以认为完成了“靠近障碍物”指令，开始实现状态转移。

（2）避开障碍物

当机械臂执行“避开障碍物”指令时，其中最为重要的一个环节是如何安全地绕开障碍物。如图3 显示了最为典型的机械臂绕行障碍物的轨迹。

图3 机械臂避障轨迹图Fig.3 Trajectory diagram of robotic manipulator obstacle avoidance

根据图3，本文所设计的“避开障碍物”指令的奖励函数如公式（3）所示：

2 基于语音奖励函数的DPPO轨迹规划

虽然DPPO方法采用惩罚项机制，为机械臂在未知环境中的规划策略提供了合理的更新比例，从而有效提升了方法的性能。但是DPPO 奖励函数只关注轨迹规划的结果而忽略了中间过程，仍然具有盲目性、学习效率低的问题。为了提高轨迹规划的学习效率，本文基于DPPO的方法增加了所设计的语音奖励函数。在DPPO学习过程中，可以为DPPO提供更加具有教学性质的奖励值，在学习过程中通过获得的语音奖励函数的有效引导，从而增强DPPO对环境的认知，进一步提高DPPO的学习效率。

基于语音奖励函数的轨迹规划学习过程如图4 所示。首先对操作员的四条语音指令L进行语音识别，并通过随机初始化构成智能体的策略网络μ(S,L|θμ)、估值网络Q(S,L,a|θQ)以及惩罚项KL。其中估值网络负责评判动作的价值，θQ表示估值网络Q的权重，策略网络负责预测应执行的动作轨迹，θμ表示策略网络μ的权重；然后使用S存储机械臂的8个最邻近时刻的相对距离，其中，Dobstacle表示机械臂在当前时刻t与障碍物的相对距离，Dtarget代表机械臂在当前时刻t与目标点的相对距离。利用语音指令的全局信息和相对距离的局部信息设计奖励函数，当相对距离满足某一语音指令状态时，根据相对距离与语音指导的契合程度对机械臂进行奖励或惩罚，进而获得一定的奖励值R，通过累计4个不同语音指令的奖励值R，得到总体的语音奖励函数Rvoice=F(S,L)。利用DPPO 的方法对语音奖励函数进行优化，经过对策略网络和估值网络的训练，智能体可以与环境更好地互动，不断修正动作偏差，寻找最优化的运动轨迹。算法1 展示了基于语音奖励函数的DPPO轨迹规划方法伪代码。

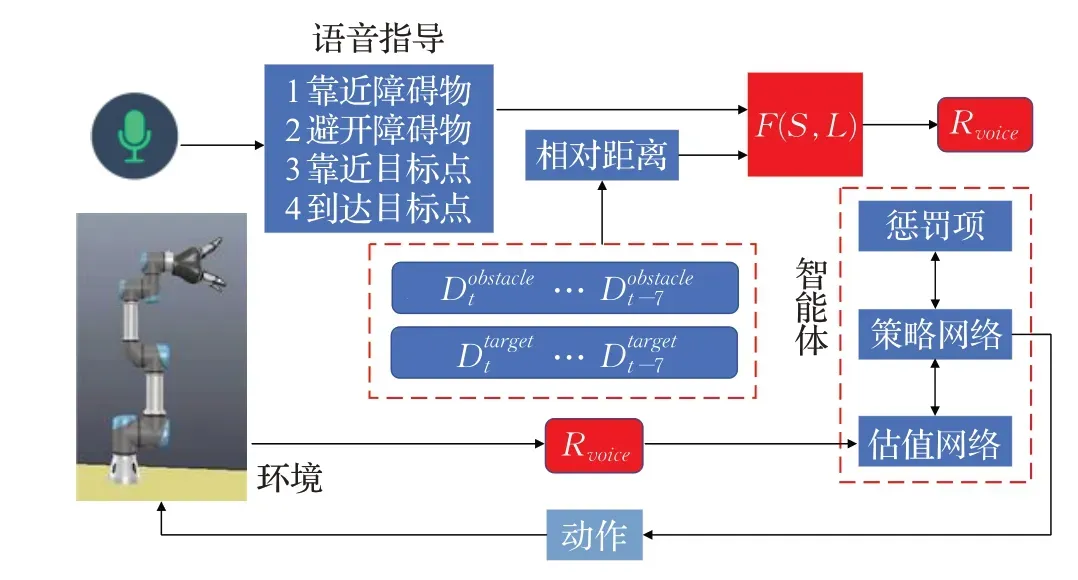
图4 基于语音奖励函数的轨迹规划框架图Fig.4 Framework diagram of trajectory planning based on voice reward function

算法1 基于语音奖励函数的DPPO 机械臂轨迹规划方法

3 实验结果与分析

本文基于科大讯飞AIUI评估板作为语音识别的载体。搭载了AIUI的评估板提供了一套开发任务型对话的解决方案，开发者可以通过在平台编写自定义技能，实现自身所需要的语音识别功能。本文基于AIUI评估板提供的SDK，开发了可供机械臂进行轨迹规划的语音识别功能。

为了验证基于语音奖励函数的DPPO 轨迹规划方法的性能，本文设计了两组实验。在第一组实验中，对比了基本的DPPO 方法和基于语音奖励函数的DPPO方法，通过比较收敛速度和奖励值的均值与标准差验证所设计语音奖励函数的有效性。第二组实验将基于语音奖励函数的DPPO 方法和当前主流的深度强化学习方法DDPG 和A3C 进行了比较，对基于语音奖励函数DPPO方法的鲁棒性和学习效率进行进一步验证。

本文所有实验均设置在难度不同的两种未知环境中，且都存在障碍物，并利用V-REP 环境进行仿真。如图5展示了两个不同的未知工作环境，工作环境包含桌子、UR3 机械臂、圆柱形障碍物以及球形目标点。其中在工作环境A 中，一个障碍物离目标稍远，表示对规划任务干扰较小。对于工作环境B，在距离目标更近的位置放有两个障碍物，在这种情况下，轨迹规划需要考虑两个障碍物之间的距离，而障碍物之间距离的不同会影响安全距离。与环境A相比较，两个障碍物对规划任务的干扰较大。在以下所有实验中，均设置奖励最大值为2 000，当奖励值稳定达到该上限的90%时，可以认为完成了轨迹规划任务。

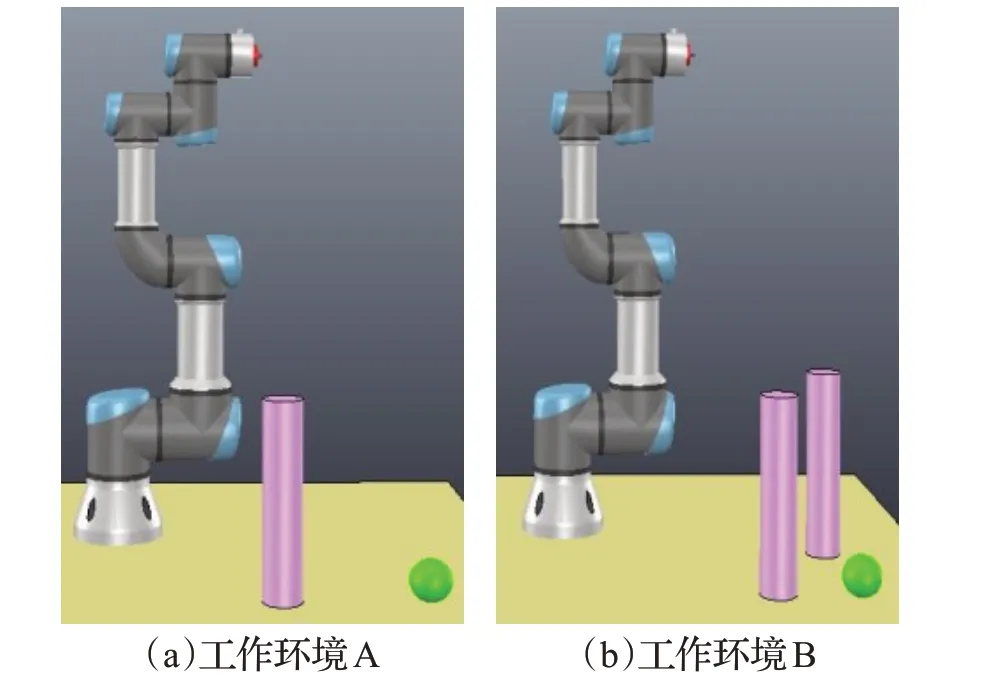
图5 机械臂工作环境图Fig.5 Working environment diagram of robot arm

表1显示了本文的实验环境配置。

表1 实验环境配置Table 1 Configuration of experimental environment

3.1 基于语音奖励函数的DPPO性能分析

本文在两种不同工作环境中都进行了30次重复实验，每次实验前都随机初始化障碍物的位置。为了进行鲁棒性对比，表2 展示了是否使用语音奖励函数的DPPO 方法收敛之后获得奖励值的均值和需要幕数的均值，并在图6中绘制了相应的奖励函数曲线图用于学习效率的评估。

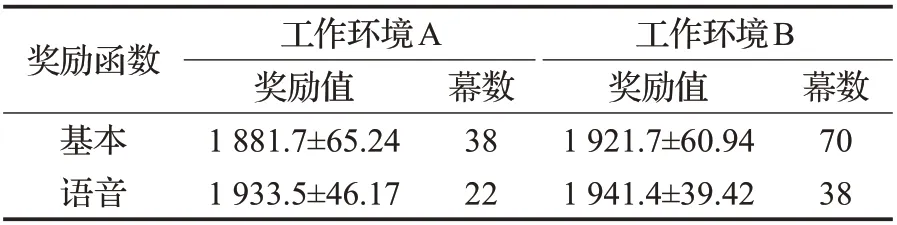
表2 DPPO是否使用语音奖励函数对比Table 2 Comparison of whether DPPO uses voice reward function

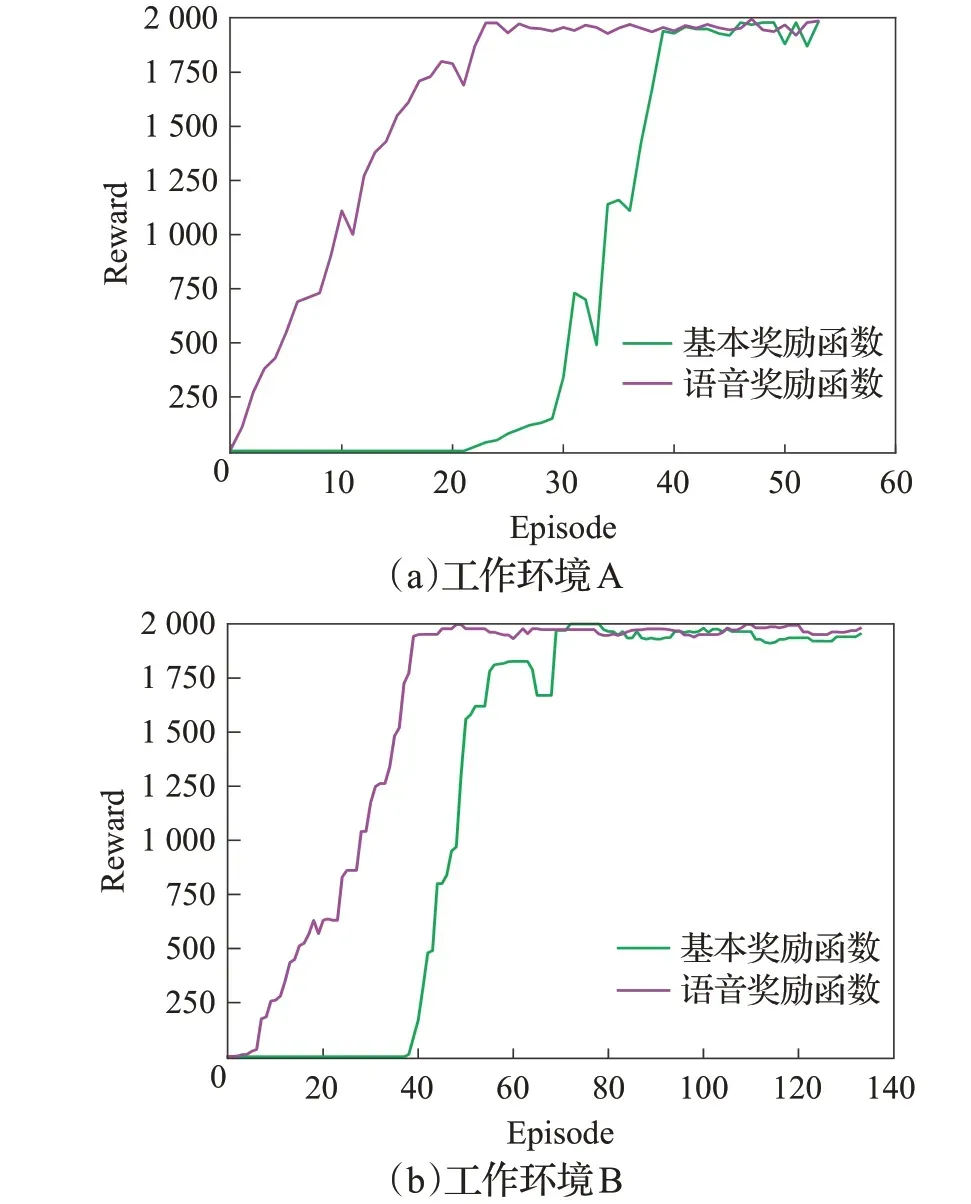
图6 DPPO奖励函数曲线图Fig.6 Curve of DPPO reward function

根据图6 可以看出，在两种工作环境中，基于语音奖励函数的DPPO 轨迹规划方法的收敛速度明显优于基本的DPPO方法，并且值得注意的是，在学习前期，基于语音奖励函数的规划方法有更加明显的提升效果。这是由于在学习的初级阶段，DPPO并不了解需要执行的任务，当在这个时期得到关于语音的指导时，DPPO则会很快地了解任务，从而提升DPPO的收敛速度。而在学习后期，智能体可以自主学习规划轨迹任务，相比学习初期，语音指导的重要性降低，所以后期基于语音奖励函数的DPPO方法与基本方法相比，学习效率提升相似。图6 的工作环境B 中表明高难度的工作环境对轨迹规划任务造成了一定的困扰，但是和基本的DPPO方法相比，基于语音奖励函数的DPPO轨迹规划方法收敛速度更快，这是因为基于语音奖励函数的DPPO轨迹规划方法通过语音的指导，减少了高难度工作环境对轨迹规划造成的影响，因此仍然能够保持比较快的收敛速度。

表2更加直接地表明了基于语音奖励函数的DPPO方法与基本方法相比具有更高的学习效率，在较少的幕数下获得了更大的奖励值，相比基本的DPPO 方法，收敛速度提高了43.8%，并且，基于语音奖励函数的DPPO方法的鲁棒性更好，其中，均值有1.95%的提升，标准差下降了32.2%。

根据实验1可以证明，在两种不同难度的未知工作环境中，基于语音奖励函数的DPPO方法可以保持更好的性能，与基本的DPPO 方法相比，收敛速度提高了43.8%，而且鲁棒性更好。

3.2 不同深度强化学习方法的性能对比

为了进一步验证本文所提出的基于语音奖励函数的DPPO方法的有效性，本节将所设计方法与当前主流的深度强化学习方法DDPG 和A3C 方法在学习效率与鲁棒性两个方面进行了对比。

（1）与DDPG方法的对比

如图7绘制了在环境A中，基于DDPG 的方法是否使用语音奖励函数的奖励曲线图，并在表3中统计了相应奖励值的均值和标准差。可以看出，由于DDPG方法学习能力有限，在工作环境B 中经过长时间的训练，DDPG仍然没有收敛。因此，下文所设计的实验仅基于实验环境A和DDPG方法进行对比。

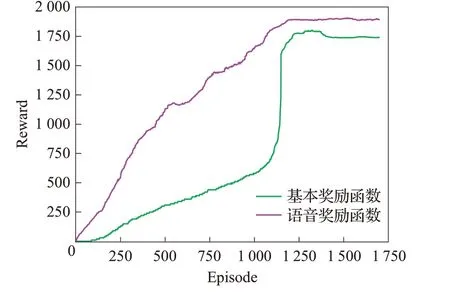
图7 DDPG奖励函数曲线图Fig.7 Curve of DPPG reward function

表3 DDPG是否使用语音奖励函数对比Table 3 Comparison of whether DPPG uses voice reward function

图7 表明，在学习效率方面，基于语音奖励函数的DDPG轨迹规划方法明显优于基本的DDPG方法，与基本DDPG 方法相比收敛速度也有25.7%的提升，并且基于语音奖励函数的DDPG方法鲁棒性更好，其中奖励均值有7.5%的提高，而标准差也下降了14.8%。

由图6和图7可以看出，在收敛速度方面，基于语音奖励函数的DPPO 方法均优于基本的DDPG 方法和基于语音奖励函数的DDPG方法，在较少的幕数下获得了更大的奖励值。在收敛速度方面，与基本的DDPG方法相比，基于语音奖励函数的DPPO方法快了21倍左右。

表2和表3总体上表明，基于语音奖励函数的DPPO方法具有更好的鲁棒性。与基于语音奖励函数的DDPG方法相比，奖励均值提升了6.5%，标准差下降了66.9%。

根据上述可得，本文所设计的语音奖励函数具有一定的适应性，同样适用于DDPG 方法。通过DDPG 和DPPO 方法的对比，进一步说明，基于语音奖励函数的DPPO 方法相比DDPG 方法具有更高效的性能，并且鲁棒性更好。

（2）与A3C方法的对比

如图8 所示绘制了两种环境下基于A3C 方法的奖励曲线图，并在表4中对所获奖励值的均值和标准差进行了统计。

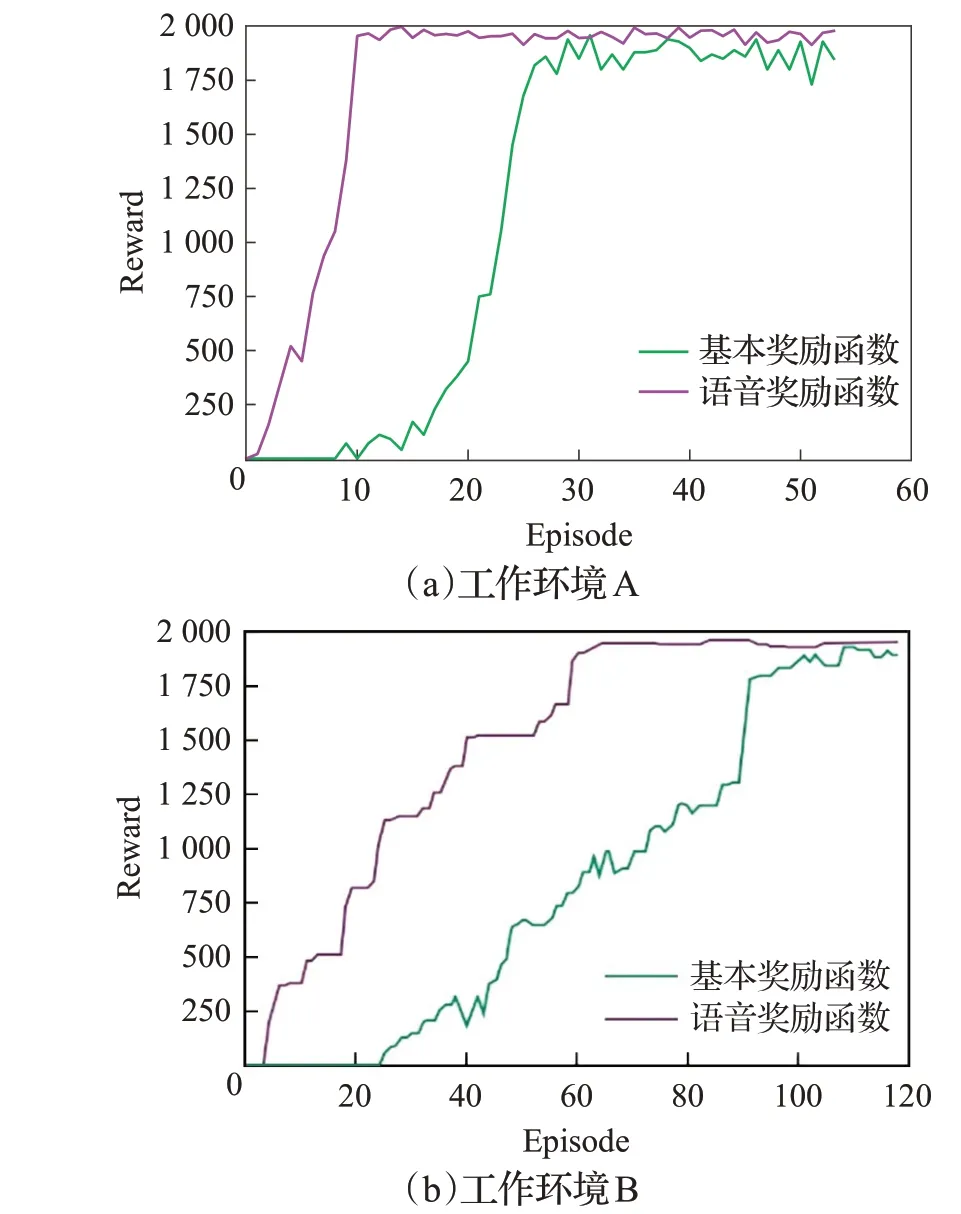
图8 A3C奖励函数曲线图Fig.8 Carve of A3C reward function

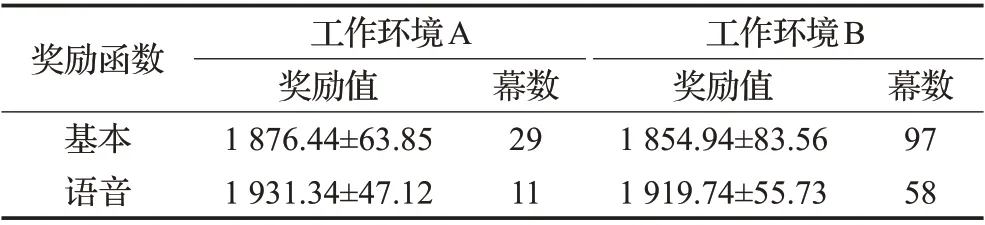
表4 A3C是否使用语音奖励函数对比表Table 4 Comparison of whether A3C uses voice rewardfunction

图8 显示，在两种工作环境中，将A3C 方法与本章所设计的语音奖励函数结合后，与基本的A3C 方法相比，具有更高的学习效率。在难度相对较低的工作环境A中，基于语音奖励函数的A3C方法相比基本的A3C方法收敛速度提升了62.1%，即使在较高难度的工作环境下，基于语音奖励函数的A3C方法收敛速度也有40.2%的提升。

结合图7和图8可以看出，在两种不同工作环境下，基于语音奖励函数的DPPO 方法在收敛速度方面均优于基本的A3C 方法。其中在工作环境A 中收敛速度提升了24%，在工作环境B中收敛速度提升了60.8%。

通过表2 和表4 对比可知，基于语音奖励函数的DPPO方法与A3C方法相比不仅收敛速度更快，而且鲁棒性更好。其中在工作环境A中，基于语音奖励函数的DPPO方法均值与A3C方法相比提高了3.1%，标准差下降了27.7%，在工作环境B中，均值提高了4.6%，标准差下降了52.8%。

3.3 讨论

在不同环境下，对基于语音奖励函数的DDPO、DDPG、A3C 方法进行30 次重复实验后，本节对不同方法所获奖励值的均值、标准差以及收敛需要的幕数，进行了可视化分析。如图9 和图10 所示，其中，纵坐标分别为奖励值和幕数。可以看出，在本文所设计的对比实验下，本文所提出的基于语音奖励函数的轨迹规划方法，在不同的工作环境中相比其他方法均取得了较高的学习效率和较好的鲁棒性。

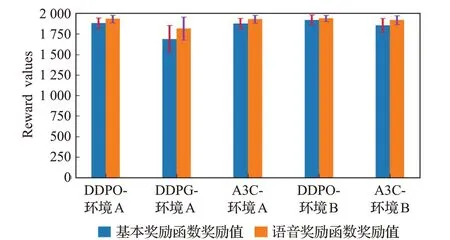
图9 奖励值可视化对比Fig.9 Visual comparison of reward values

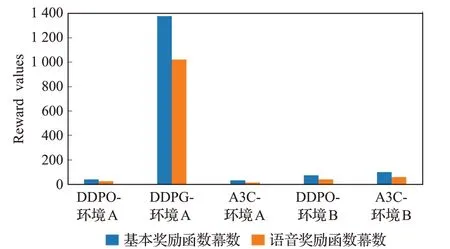
图10 幕数可视化对比Fig.10 Visual comparison of number of acts

4 结束语

本文提出了一种基于语音奖励函数的机械臂轨迹规划方法。通过设计一种语音奖励函数，有效地解决了无效探索导致学习效率偏低的问题。将DPPO 方法用于未知工作环境中的机械臂轨迹规划任务，提高了规划策略的鲁棒性。实验证明本文提出的基于语音奖励函数的DPPO 方法在不同难度的未知工作环境中均取得了良好的效果，学习效率更高，具有很高的适用性。但是仅能实现单一目标点的机械臂轨迹规划，而在真实工作环境中，有些任务的目标点为多个。未来考虑将本文方法推广到多目标轨迹规划。