预测水泥砒砂岩强度的Markov灰色残差模型
刘鑫,申向东, 景宇,任杰,吕昕,耿凯强,董国际,郝政凯
(1. 内蒙古农业大学水利与土木建筑工程学院,内蒙古 呼和浩特 010018;2. 鄂尔多斯应用技术学院土木工程系,内蒙古 鄂尔多斯 017010;3. 鄂尔多斯市住房和城乡建设局建设工程质量监督站,内蒙古 鄂尔多斯 017010)
砒砂岩是由侏罗纪和白垩纪的泥质砂岩组成的砂岩交互层,砂岩颗粒间的胶结程度弱、结构强度低、成岩度差[1].砒砂岩主要分布在晋陕蒙接壤地区的鄂尔多斯高原,面积约为1.67万km2,侵蚀模数高达2~4万t/(km2·a),水土流失非常严重,给当地的生态环境造成了极其恶劣的影响[2].
目前主要是通过实验室测试砒砂岩或改性砒砂岩的抗压强度[3-4],如果想要获得长龄期、多种工况的抗压强度数据,势必会费时且费力.为此,有必要借助数学模型依据有限的样本来探究一种可靠的强度预测方法.灰色系统理论在数据处理方面,与基于回归分析的传统方法相比有明显的优势[5-6],甚至比需要大量训练样本的神经网络以及具有平移不变性和池化层的卷积神经网络更方便[7-10].
灰色系统理论中的GM(1,1)模型具有计算简便、易于检验和对历史数据要求少等优点,可以用来预测事物的发展规律[11].尽管灰色GM(1,1)模型有诸多优点,但是如果数据的离散性比较大,则该模型的预测精度比较低,残差比较大.为此,提出灰色残差GM(1,1)模型[12],但该模型的适用范畴也有局限,如果残差序列有正、有负的情况下,将无法判定残差预测值的正、负号.针对该问题,尝试把马尔克夫过程引入灰色残差GM(1,1)模型中,建立样本需求少、预测精度高的马尔克夫过程灰色残差GM(1,1)预测模型(以下简称:Markov-灰色残差GM(1,1)模型),并预测水泥砒砂岩的抗压强度,从而检验该模型在水泥固化砒砂岩以及其他样本少而离散的水泥基工程材料领域中的适用性.
1 灰色模型
1.1 灰色GM(1,1)模型
根据上述定义建立的灰色GM(1,1)模型为
x(0)(k)+az(1)(k)=b,k=1,2,...,n,
(1)
式中:a为发展系数;b为灰色作用量;变量a,b的具体求解见文献[12].
构建灰色微分方程:
(2)
(3)
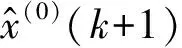
(4)
1.2 灰色残差GM(1,1)模型
k=2,3,...,n,
(5)

(6)
1.3 灰色模型精度检验
灰色模型的建模精度需检验合格后方可用于预测第(k+1)个的值.灰色模型精度检验一般有3种方式:后验差检验、小误差概率检验以及关联度检验,具体计算公式详见文献[13].常用的精度检验等级如表1所示[14],表中C为后验差比值,P为小误差概率,γ为关联度.
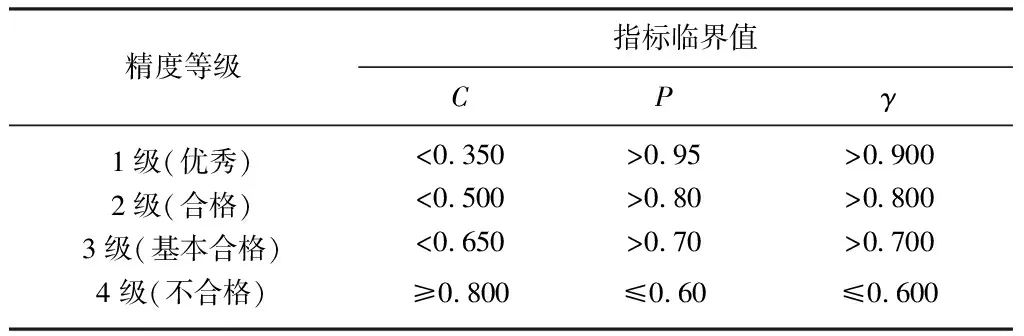
表1 精度检验等级参照表
1.4 马尔克夫过程
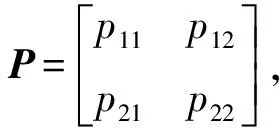
2 应用实例
2.1 材料与方法
砒砂岩选自内蒙古鄂尔多斯市康巴什北区,将所取的重塑砒砂岩样自然风干、碾压并过2.36 mm的方孔筛,砒砂岩的物理指标:天然含水率4.83%~6.92%;天然密度为1.63~1.69 g/cm3;风干含水率为1.9%~2.1%;最优含水率为14.5%;最大干密度为1.77 g/cm3;液限为27.6%;塑限为18.3%;塑性指标为9.3.砒砂岩的级配曲线见图1,图中α1为累积分布,D1为密度分布,D为粒径.XRD物相分析见图2.由图1可知,该土样的黏粒质量分数(颗粒直径<5 μm)为0,粉粒质量分数(颗粒直径5~75 μm)为9.39%,砂粒质量分数(颗粒直径>75 μm)为90.61%,说明该土样为砂土且为细砂土.由图2发现,砒砂岩的主要矿物成分为石英、蒙脱石、云母、斜长石、方解石、微斜长石和高岭石.水泥为蒙西P·O42.5普通硅酸盐水泥,水为普通自来水.
参照《土工试验方法标准》(GB/T 50123—2019)和《公路工程无机结合料稳定材料试验规程》(JTG E51—2009)的相关规定.采用静力压实的方法将最优含水率下的水泥砒砂岩混合物(水泥掺量分别为4%,7%和10%)装入直径为50 mm,高为130 mm的钢试模中,压成直径为50 mm,高为50 mm的圆柱体(每组3个平行试样).试样脱模后放入标准养护箱养护至规定龄期,利用WDW-50 型万能试验机以1 mm/min的加载速率,分别对养护至7,14,21,28,60和90 d龄期的试样进行无侧限抗压强度试验.
2.2 结果与分析
不同龄期下水泥砒砂岩的无侧限抗压强度如表2所示,表中σ为抗压强度.以7,14,21,28和60 d龄期的抗压强度为建模数据建立灰色GM(1,1)模型和灰色残差GM(1,1)模型并检验模型的模拟精度,在此基础上以60 d龄期的抗压强度为原始数据构建Markov-灰色残差GM(1,1)模型.根据模型预测养护龄期90 d的抗压强度,并与实际值进行比较,从而研究Markov-灰色残差GM(1,1)模型在水泥固化砒砂岩中的适用性.
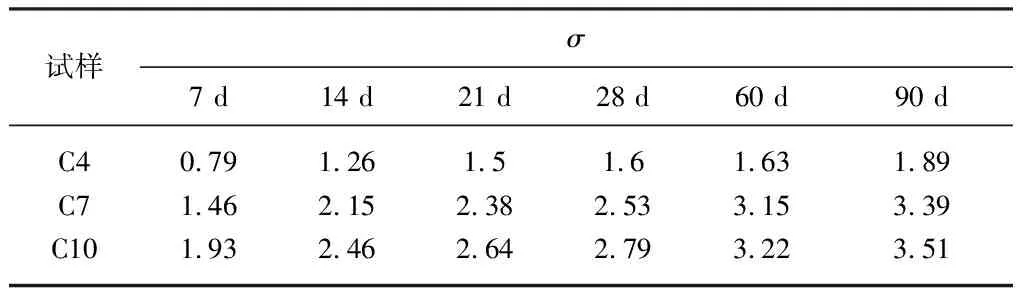
表2 不同养护龄期的水泥固化砒砂岩抗压强度
设x(0)为水泥固化砒砂岩的抗压强度,依据式(1)建立的灰色GM(1,1)模型为
x(0)(k)+az(1)(k)=b,k=1,2,...,5.
(7)
该模型是以7,14,21,28和60 d龄期的抗压强度经过1次累加生成的序列为建模集,将水泥掺量4%,7%和 10%的建模数据分别代入式(1)—(4)中得到对应水泥掺量的灰色GM(1,1)预测模型,如式(8)—(10)所示;同理把水泥掺量4%,7%和 10%的建模数据代入式(5)—(6)中得到灰色残差GM(1,1)模型.如式(11)—(13)所示.
灰色GM(1,1)模型:
(8)
(9)
(10)
灰色残差GM(1,1)模型:
(11)
(12)
(13)
以水泥掺量4%为例来验证所建模型的模拟精度,2种灰色模型的模拟值和试验值的对比如图3所示,图中T养护龄期.
由图3a可知,2种模型的模拟值与试验值都比较接近,但是灰色残差GM(1,1)模型的拟合效果(R2=0.977)明显优于灰色GM(1,1)模型(R2=0.806),并且对于估算值与试验值之间的偏差,灰色残差GM(1,1)模型(RMSE=0.01)同样小于灰色GM(1,1)模型(RMSE=0.06);从图3b发现,灰色GM(1,1)模型的相对误差ε为2.91%~4.40%,平均值为3.46%,灰色残差GM(1,1)模型的相对误差为0.28%~0.84%,平均值仅为0.58%.由此可见,灰色残差GM(1,1)模型的模拟精准度远高于灰色GM(1,1)模型.
为了全面比较灰色GM(1,1)模型和灰色残差GM(1,1)模型的精度,选取后验差比值C,关联度γ以及小误差概率P对建模精度进行检验,3种试样(C4,C7和 C10)的检验值比较如表3所示,由表可知,灰色GM(1,1)模型模拟结果的后验差比值为0.322~0.398,其平均值为0.362;关联度为0.606~0.647,其平均值为0.627.根据表1可知,后验差比值精度为2级,关联度精度为4级.灰色残差GM(1,1)模型模拟结果的后验差比值为0.069~0.192,其平均值为0.143;关联度为0.818~0.928,其平均值为0.862,小误差概率为1.00;根据表1可知,后验差比值精度为1级,关联度精度介于1—2级,小误差精度为1级.由此可以发现,灰色残差GM(1,1)模型的检验精度等级明显得到了提升,且各项检验指标基本上都达到了1级.

表3 检验值比较
经计算,试样C4,C7和C10的残差修正的正负号分别为正、负和正.灰色GM(1,1)模型和Markov-灰色残差GM(1,1)模型对90 d龄期3种水泥固化砒砂岩抗压强度的预测结果如图4所示.
由图4a可知,Markov-灰色残差GM(1,1)模型的拟合度R2和拟合偏差RMSE指标同样优于灰色GM(1,1)模型;由图4b可知,Markov-灰色残差GM(1,1)模型预测抗压强度的最大相对误差为2.36%,平均相对误差仅为1.25%,预测精度明显高于灰色GM(1,1)模型(最大相对误差为4.01%,平均相对误差为2.63%),Markov-灰色残差GM(1,1)模型相比传统灰色GM(1,1)模型平均相对误差降低52.50%.由此可见,灰色GM(1,1)模型经残差修正后,在利用马尔克夫过程判定残差修正值正负号的基础上得到的预测结果更逼近于真实值.综上可知,Markov-灰色残差GM(1,1)模型能有效判定残差修正值符号,并且有很高的精准度来预测水泥砒砂岩的抗压强度,该模型可以为水泥基材料抗压强度的预测提供技术支撑和理论借鉴.
3 结 论
1) 灰色GM(1,1)模型模拟结果的后验差比值精度为2级,关联度精度为4级;灰色残差GM(1,1)模型模拟结果的后验差比值精度为1级,关联度精度介于1—2级,小误差概率精度为1级,各项检验指标基本上都达到了1级.
2) 在借助马尔克夫过程确定预测数据残差修正值所处的正、负符号的基础上,以残差修正值对灰色GM(1,1)模型进行了修正,构建了Markov-灰色残差GM(1,1)模型.该模型对养护龄期90 d的水泥固化砒砂岩(水泥掺量为4%,7%和 10%)的抗压强度进行了预测,结果表明,相对误差由原来的1.77%~4.01%降低至0.60%~2.36%,平均相对误差由2.63%减小至1.25%,降低了52.50%,提高了预测精度.
3) Markov-灰色残差GM(1,1)模型在保留了传统灰色GM(1,1)模型试验样本少、计算方便和容易检验等优点的基础上,在一定程度上拓宽了灰色理论的应用范畴,为水泥基材料抗压强度的预测提供了一种简单而可靠的新方法.

