一道2022年北京高考数学试题的分析与推广
邱和保
(福建省连江第一中学,福建连江,350500)
圆锥曲线问题是高考必考的大题之一,通过对2022年全国高考试卷进行分析可以发现圆锥曲线问题的分布情况如表1所示.根据表1的数据可以发现圆锥曲线问题在整张试卷中占到19到22分,正如《中国高考评价体系》中所强调的:高考必须坚持引导教学.[1]因此要对圆锥曲线问题进行重点研究,抓住其本质,研究其内涵,这不仅有利促进教师对高考的把握,对提升学生的数学学习也有着重要的作用.
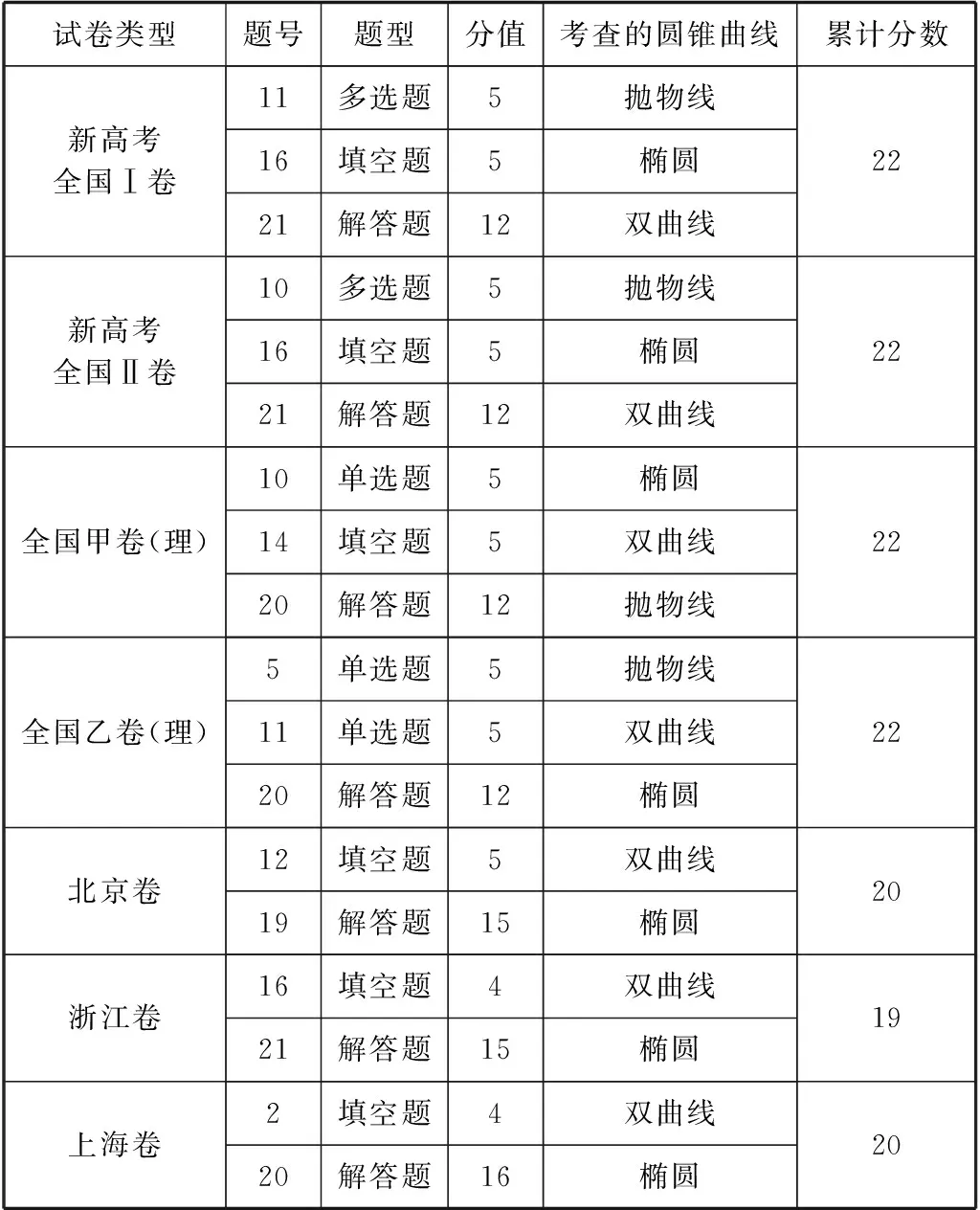
表1 2022年高考试卷中圆锥曲线问题分布
下面以2022年北京高考数学第19题为例进行具体研究:
1 试题呈现
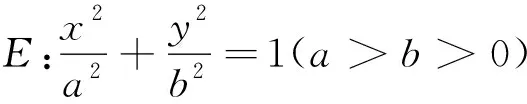
(1) 求椭圆E的方程;
(2) 过点P(-2,1)作斜率为k的直线与椭圆E交于不同的两点B、C,直线AB、AC分别与x轴交于点M、N,当|MN|=2时,求k的值.
2 意图分析
本题有两个小问,问题一主要考查椭圆的标准方程,要求学生能够读取题目信息,建立起对应元素和数量间的关系,根据a,b,c求椭圆方程;问题二主要考查直线与椭圆的位置关系、韦达定理和弦长公式等,并利用这些公式求出参数k.两小问对学生的数学能力都有所要求,充分在试题中渗透了数学学科核心素养.
3 解题思路
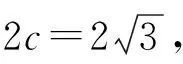
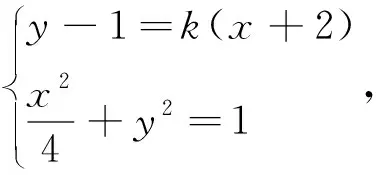
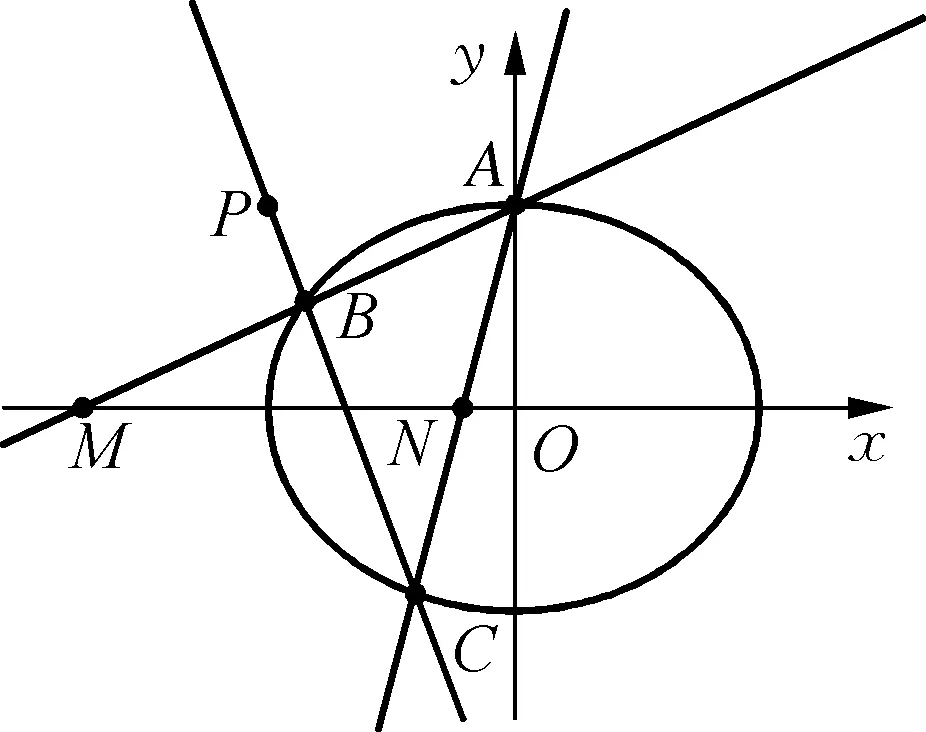
图1
评析:多数学生可以比较容易地解出第(1)题,但是对于第(2)问大多数学生可能都会想到根据直线与椭圆的位置关系联立直线与椭圆方程,然后利用韦达定理,写出两根之和和两根之积的表达式,但是接下去就没了思路.教师在讲解的时候要注意数形结合,引导学生分析题目,从要求的问题出发.要求参数k,所给的条件有|MN|=2,必然要想到利用弦长公式求解,转问题为求M、N的坐标,又因为M、N分别为直线AB、AC与x轴交点,所以需要求直线AB、AC的方程.由于A是确定的点,所以要从B、C两点入手才能解出题目.教师应该在教学过程中培养学生的解题思路,让学生掌握解一类题的方式方法,而不仅仅是解出一道题.
4 试题推广
下面给出题目的一般化形式:
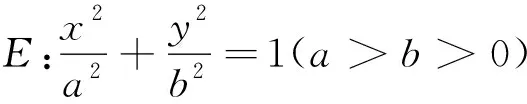
证明:如图2所示,由题意可得lBC:y-b=k(x+a)

图2

得(b2+a2k2)x2+(2a3k2+2a2bk)x+a4k2+2a3bk=0,
∵Δ=(2a3k2+2a2bk)2-
4(b2+a2k2)(a4k2+2a3bk)>0,
∴k<0,
设B(x1,y1)、C(x2,y2),且-a 通过观察发现把试题中得椭圆改为圆,有下面得结论成立: 图3 证明过程与推广1的证明方法类似,下面就不再赘述. 其实在数学教学的过程中,培养学生解题的思路是教学的重点也是难点,学生是具有独特性质的个体,有自己学习的思维,不是应试的机器.正如《普通高中数学课程标准(2017年版2020年修订)》中提到的:遵循教育教学规律和学生身心发展规律,贴近学生的思想、学习、生活实际,充分反映学生的成长需要,促进每个学生主动地、生动活泼地发展.[2]因此不管是考试还是日常都应该强化学生对知识的理解,在解题过程中渗透数学思想方法,特别是在解决直线与圆锥曲线的问题中,要强化联立直线与圆锥曲线的方程的意识,并结合韦达定理,列出根与系数的关系,然后逐层递进,找到问题与条件的内在关系,从而解决问题.
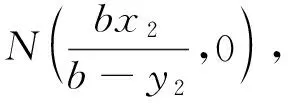

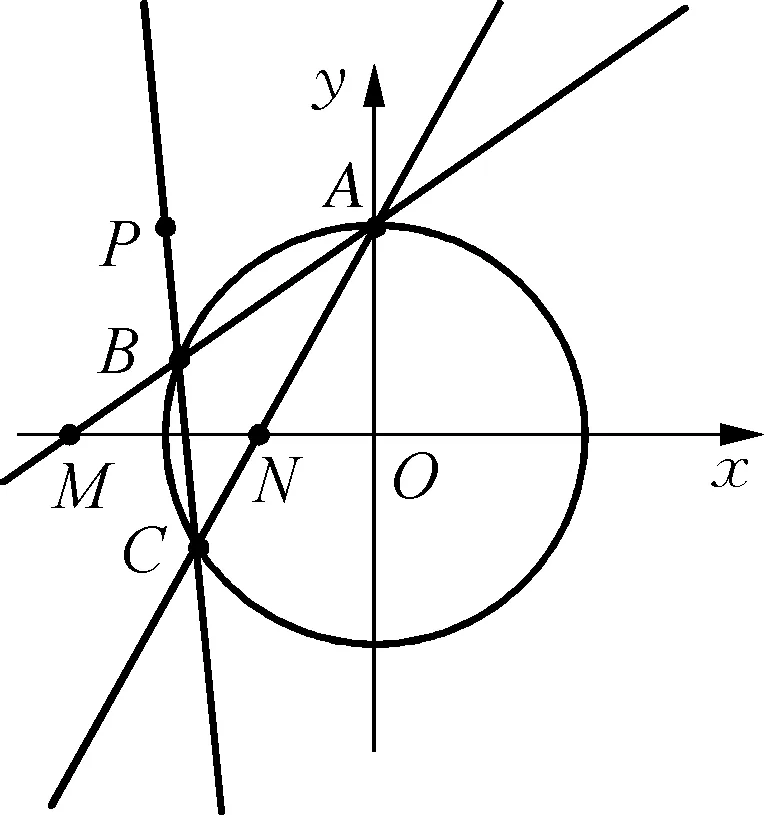
6 解题思考

