一道初中数学试题的来路、思路、去路

程永超

(江苏省常州市花园中学，江苏常州，213000)

一道好的试题不仅在内容上能够检测学生对核心知识的掌握情况，还能考查学生运用数学的思维及分析、解决问题的能力.在此基础上，形式优美，体现一定的原创性，则效果更佳.本文记录了一道试题的来路、思路、去路，希望通过这个实例，说明命题编制的一些方法与技巧，敬请同行们批评指正.

1 命题来源，定性分析到定量确定

在平面内，给定一个点、一条直线，我们能画出该点关于这条直线的对称点，如图1所示.

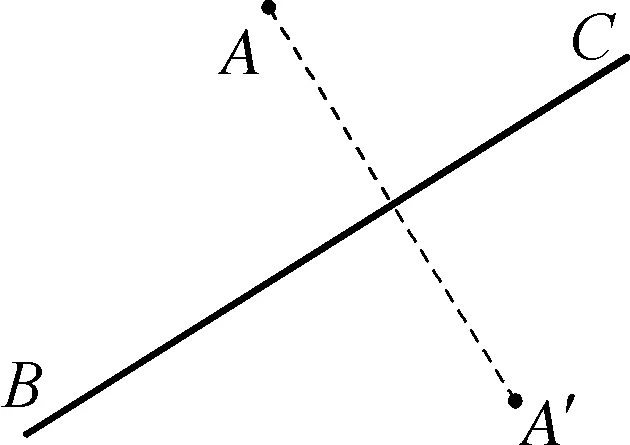
图1

思考一：如图2，如果把点A跟直线BC放在平面直角坐标系中，能否求出对称点A′的坐标呢？

图2

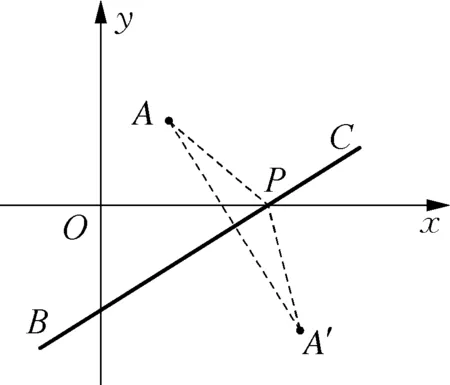
图3

给定点A的坐标、直线BC的解析式，对称点A′是唯一确定的，所以坐标是可求的.

求法一：如图2，设点A′(x，y)，考虑到线段AA′被直线BC垂直平分，所以KAA′·KBC=-1，AA′的中点坐标符合直线BC的解析式，从而得出x，y的方程组，求出x，y的值.但是两条直线互相垂直，能满足KAA′·KBC=-1，这不在初中数学学习的范围里.

求法二：如图3，直线BC与x轴的交点P是已知点，则线段AP的长度、∠APB的度数都是已知，所以可以根据三角函数求出点A′的坐标.但即使∠APB的度数是已知的，但一般来说，不会是一个特殊的度数，所以，在初中数学范围内，知道点A′是已知的，但不好求.

思考二：在初中数学范围内，怎样调控一下，使得对称点A′的坐标容易求些？

1.1 一般的直线+特殊的点

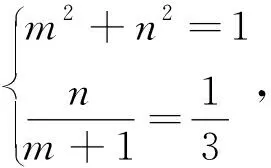
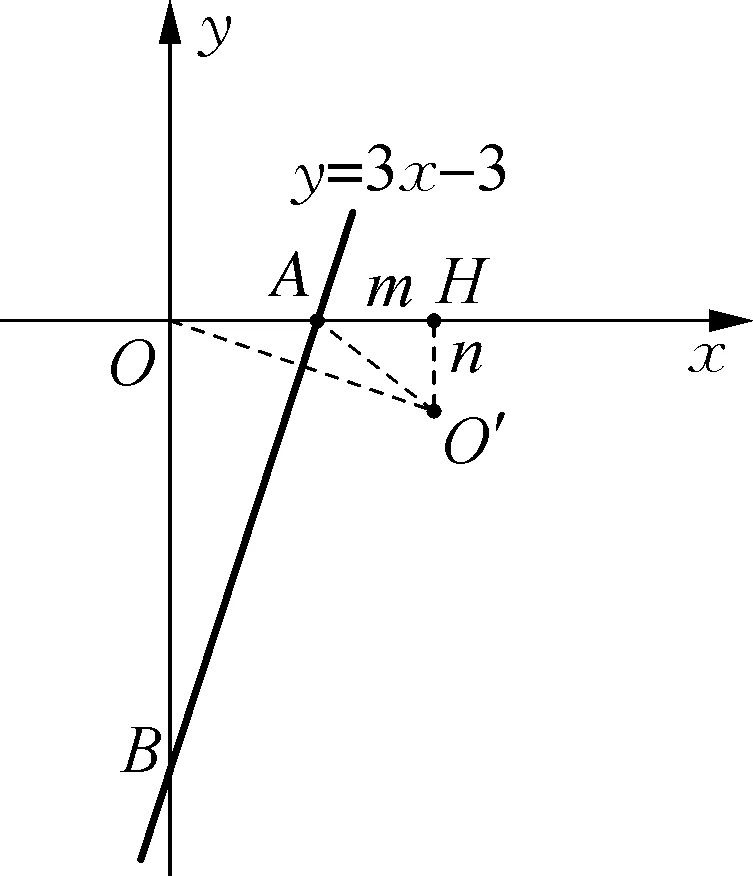
图4

图5

1.2 特殊的直线+一般的点

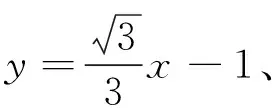
1.3 特殊的直线+特殊的点

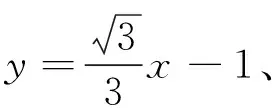
图6

图7

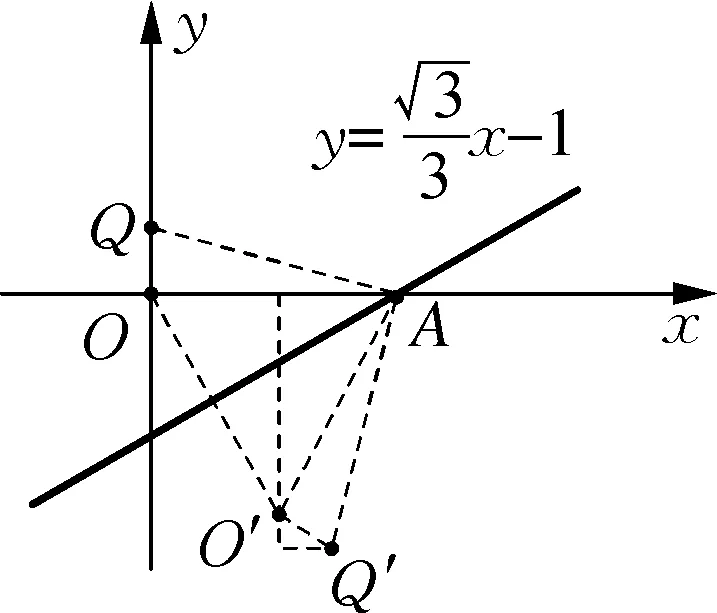
图8

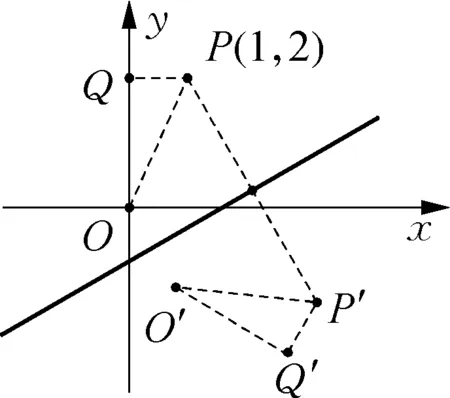
图9

据此，图5中的计算，将点P的轴对称理解成是Rt△PQO的轴对称，构造K型相似，可求点P′的坐标，如图9.但此类计算总归会涉及到相似、无理数的计算，鉴于数学试题“多想少算”的原则，能否将特殊角改成45°呢？

如图10，点O的对称点O′(2，-2)，点P(-1，0)的对称点P′(2，-3)，点Q(1，2)的对称点Q′(4，-1).可以发现，当特殊角改成了45°，不仅运算量小，而且“水平”线段，轴对称成“铅垂”线段；“铅垂”线段，轴对称成“水平”线段.那么，一般的直线，关于直线y=x-2轴对称之后，有什么特殊之处吗？

图10

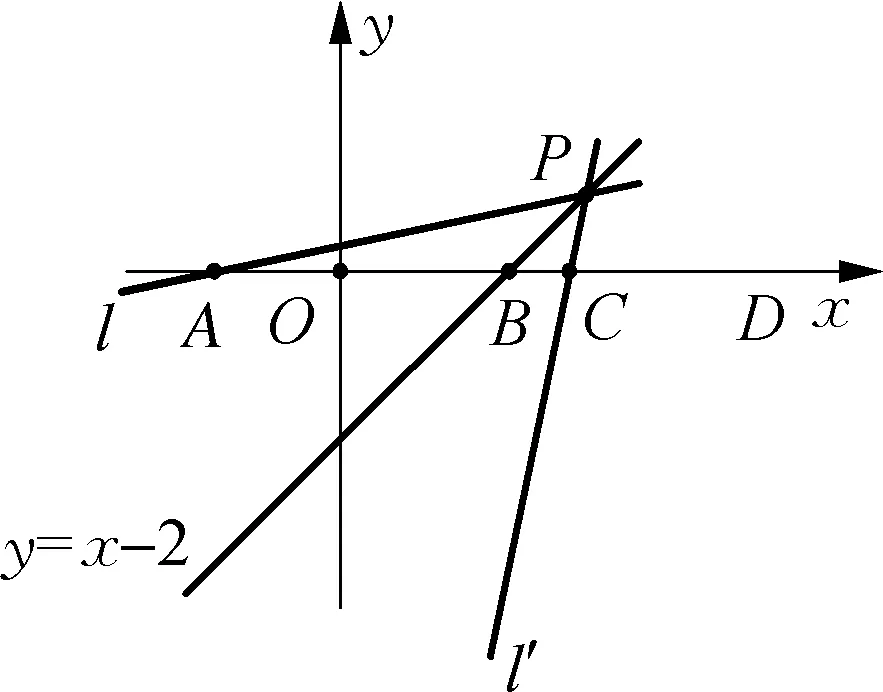
图11

如图11，由三角形的外角定理知：∠APB=45°-∠PAB，所以∠PCD=2∠APB+∠PAB=90°-∠PAB，则∠PAB+∠PCD=90°.

2 试题编制，关注核心本质、整体关联

思考三：试题该如何编制，既要考查学生的核心素养，还要注重试题的整体关联？

2.1 动态化处理[1]

将对称轴沿x轴平移，与x轴的夹角依旧是45°.这样，上述发现的一系列性质(“水平”线段，轴对称成“铅垂”线段；“铅垂”线段，轴对称成“水平”线段；一般的直线，轴对称之后，与x轴所夹锐角之和为90°)依旧成立.

2.2 搭好“脚手架”，直击核心本质

作任意一条直线的对称直线，如果不考虑其它限制的话，只要找到两个点的对称点即可(图1的方法).但为了让学生感受到上述性质，将直线放入方格纸中，仅限无刻度的直尺来作图.学生必将找格点的对称点，就能在解题的过程，领悟性质，并将领悟到的性质加以运用.

2.3 注重试题的整体关联

在新的问题情境中，为了考查学生的思维视野，能否将领悟到的经验、思维方法迁移到新问题的解决中，通过大任务渗透大观念.按点、线、面的变换线索呈现[2]，加强试题的关联度，调整后形成如下试题.

2.4 试题呈现

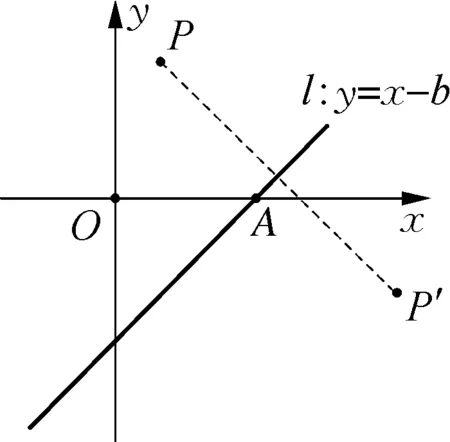
图12

如图12，动直线l：y=x-b与x轴交于点A，对于平面内一点P，我们可以作点P关于直线l的轴对称点P′，我们称点P′为点P的“斜对称点”.类似地，我们可以得到“斜对称直线”“斜对称三角形”等等.

(1) 如图12，请直接写出点O关于直线l的斜对称点O′的坐标(用b的代数式表示)；

(2) 如图13，动直线l：y=x-b与x轴、y轴分别交于格点A、格点B，直线l1与x轴交于格点C，交y轴于点D.仅用无刻度的直尺，作出直线l1的斜对称直线l2；并记直线l2与x轴所夹的锐角为α，证明α+∠DCA=90°；

图13

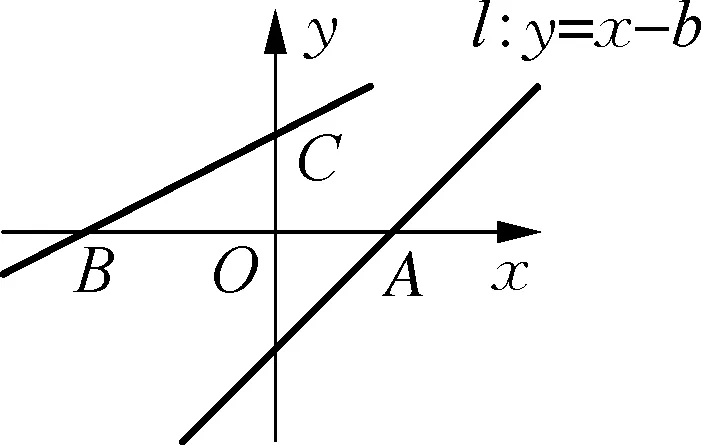
图14

3 编后反思，素养立意、强化数学思考

思考四：试题后续的研究.

在试题的第三问中，考虑到难度的控制，只考查了“水平”线段的斜对称线段.如果继续试题的后续研究，我们可以增加试题的综合性.比如，斜对称△C′O′B′与△OBC的外接圆相切，求b的值.尤其是，斜对称线段C′B′与外接圆相切的说理，可以跟第二问的证明遥相呼应.

思考五：注重数学思考，渗透大观念.

试题的命制既要注重对数学基础知识、基本技能的考查，更要关注学生对数学观念(数学思维方式、数学思想方法)的领悟与迁移.所以，在日常的数学教学中，渗透从简单到复杂(点、线、面上的图形结构依次复杂、从静到动)，从特殊到一般等研究问题一般方法.通过基于问题学习、任务性学习，让学生不仅知道“怎样做”，还要明白“为什么怎样做”.