调节阀内瞬态空化压力脉动特性分析
刘秀梅, 谢永伟, 李贝贝, 贺 杰, 陈劲松
(1.中国矿业大学 机电工程学院,江苏 徐州 221116; 2.徐州工程学院 电气与控制工程学院,江苏 徐州 221018)
空化在泵、水翼、孔板、螺旋桨、喷射泵、文丘里管等液压部件中广泛存在,通常指流体中的局部压力低于饱和蒸汽压时,空泡的形成、生长以及溃灭现象。一般来说,空化会带来诸多不良影响,如对设备表面造成侵蚀、影响机械作业精度、带来振动和噪声等。研究空化现象及其变化过程中的压力脉动具有重要意义。
现有空化研究主要有:对各液压机械中的空化流动进行数值模拟[1-3],并不断优化模型以更精准的表征空化流场变化情况[4-5],对空化结构变化原因进行研究[6-7],对空化结构演变过程中引发的压力脉动进行特性研究[8-9]等。
为探寻空化云脱落机理及其变化过程中压力脉动的原因,Long等[10]对水翼空化过程进行三维仿真计算与理论推导,研究了空穴体积变化与空穴周围压力值的数量关系。Wang等[11-12]采用试验与数值模拟相结合,研究了收敛-扩散通道内空泡脱落、溃灭过程,对反射流以及激波机制下的空泡变化过程并进行分析。陈广豪[13]对收缩-扩展流道内附着型空穴的瞬态变化过程进行试验和仿真分析,并对其压力脉动特性进行了研究。张孝石通过多场同步测量试验,研究了水下航行体肩部空泡形态变化与速度、涡的关系,进一步揭示了其近壁面压力脉动特性。Zhu等[14]通过对变压比风洞试验中的液氮文氏管内空泡的动态变化过程进行分析;研究发现随着压比的增加,空泡脱落频率与空泡长度在线性增加,且幅值指数增加。韩亚东等通过将试验测量与数值模拟相结合,表明旋涡与空泡相互作用,空泡脱落由反向射流导致,并通过动力学模态分解分析了空化流动,提取其主要动力学特征。龙新平等[15]对不同空化数下文丘里管内空化引发的压力脉动进行研究,发现空化云脱落频率与文丘里管下游的压力脉动频率近似。Dastane等[16]采用数值模拟的方法对文丘里管内的空化流动进行研究,对空化过程中的空泡半径、溃灭温度及溃灭压力进行估算,建立数值模型,Pelz等[17]研究了空化变化过程与空化数及雷诺数的关系,对云状空穴的增长和反向射流流动过程进行分析。另外有一些学者研究了空泡的动力学相关特性[18]、对文丘里管内部空化流动过程进行动力学模态分解[19],推进了对空化过程中压力脉动情况的研究。本课题组通过试验和数值讨论了调节阀内稳态空化场[20],但仅局限于喉部。
上述研究主要是对水翼和文丘里管的空化研究,未深入讨论液压阀内的空化瞬态压力场的变化情况。空化也是液压系统中经常出现的一种现象,它会影响液压元件的寿命及控制精度,因此本文针对液压调节阀内瞬态流场,数值模拟了阀内周期性的空化变化过程及其压力脉动特性等,分析其空化区内部形态和变化规律,对于液压阀结构的优化设计具有重要意义。
1 数学模型
因为阀口中心对称,且在实际工程应用中空化主要发生在阀口附近,故本文的仿真模型采用液控调节阀内部流道空化旋转轴对称模型,如图1所示。在本研究中调节阀流道总长度为L=75.0 mm,其中上游段L1=21.5 mm,喉部L2=26.75 mm,扩张段L3=13 mm,L4=23.5 mm,流道总长度L=75 mm,入口和出口直径分别为15.0 mm与25.6 mm,r0=3.0 mm,r1=3.5 mm,r2=7.5 mm。

图1 几何模型Fig.1 Geometric model
从图1可知,液控调节阀内部流道几何模型,采用混合网格对全流道进行网格划分,并对液控调节阀口及下游空化区域进行局部加密。在仿真计算过程中,压力、速度等参数发在节流口处发生突变,因此在该处采用三角形网格加密划分,阀口处放大图如图2所示。加密后网格的最小网格尺寸为0.008 mm×0.008 mm。

图2 阀口放大图Fig.2 Enlarged view of the orifice
为消除网格数对计算结果的影响,需进行网格无关性验证。本文选取阀门入口的质量流率作为判断网格数是否影响流场分布的依据,发现调节阀入口的质量流率随着格数的增加而增加。当网格数达到100 000时,调节阀的质量流率不再随着网格数的增加而变化。因此,将100 000确定为网格数,且流道网格的近壁面y+大部分在30~150之间,可以满足计算速度和计算结果精度以及壁面函数的要求。
入口设置为压力入口(Pressure-inlet)边界条件,入口压力值为5.0 MPa;出口设置为压力出口(Pressure-outlet)边界条件,出口压力值为1.0 MPa;中心轴设置为axisymmetric边界条件。此外,图1中除入口、出口和中心轴以外的边界均为壁面(Wall)边界条件,近壁区选用壁面函数对其处理,壁面无滑移。
在本仿真计算中,液相和汽相被假定为等温且不可压缩。采用Fluent软件中的Mixture模型、Schnerr-Sauer空化模型[21-22]能较好的模拟液压阀内的空化流场。液压油在30 ℃时的饱和蒸汽压400 Pa。
在空化过程中,湍流黏度系数与两相流密度有关,且是一个变化值,因此此处引入修正后的RNG k-ε湍流模型,修正后的湍流黏性系数表达式为:
μt=f(ρm)Cμk2/ε,
式中:ρm为混合相密度;ρv为气相密度;ρl为液相密度。Cμ≡0.085,k为湍动能;ε为湍流耗散率,n为一常数,为了更好研究空化现象的反向射流以及大尺度空穴脱落,此处n取10。
针对上述控制方程组在空间进行离散。速度和压力的耦合由SIMPLE算法实现,压力项离散方式采用Standard格式,其它项均采用一阶迎风格式。计算时先进行稳态计算,将结果作为非定常计算的初值,从而保证计算的稳定性和收敛速度。为保证在微观时间尺度下,对空穴的脱落溃灭进行充分观测,同时尽可能的节约计算资源,此处仿真时间步长设为Δt=0.1 μs。
2 计算结果分析
基于上述数值计算模型,本文设置入口压力为5 MPa,出口压力为1 MPa,液控调节阀开度为60%(开度K=l/lmax,lmax为调节阀的总行程),对这一工况下空化流动演变的一个典型周期进行了细致分析,研究了非定常空化演变过程及其演变原因,对阀内压力脉动特性进行分析。
2.1 空穴结构演化过程
一个周期内空化结构的演化过程,如图3所示。从图3可知,包含空化的产生、脱落以及溃灭三个阶段的瞬态周期性空化发展过程在液压调节阀内发生,一个周期约为1.77 ms。

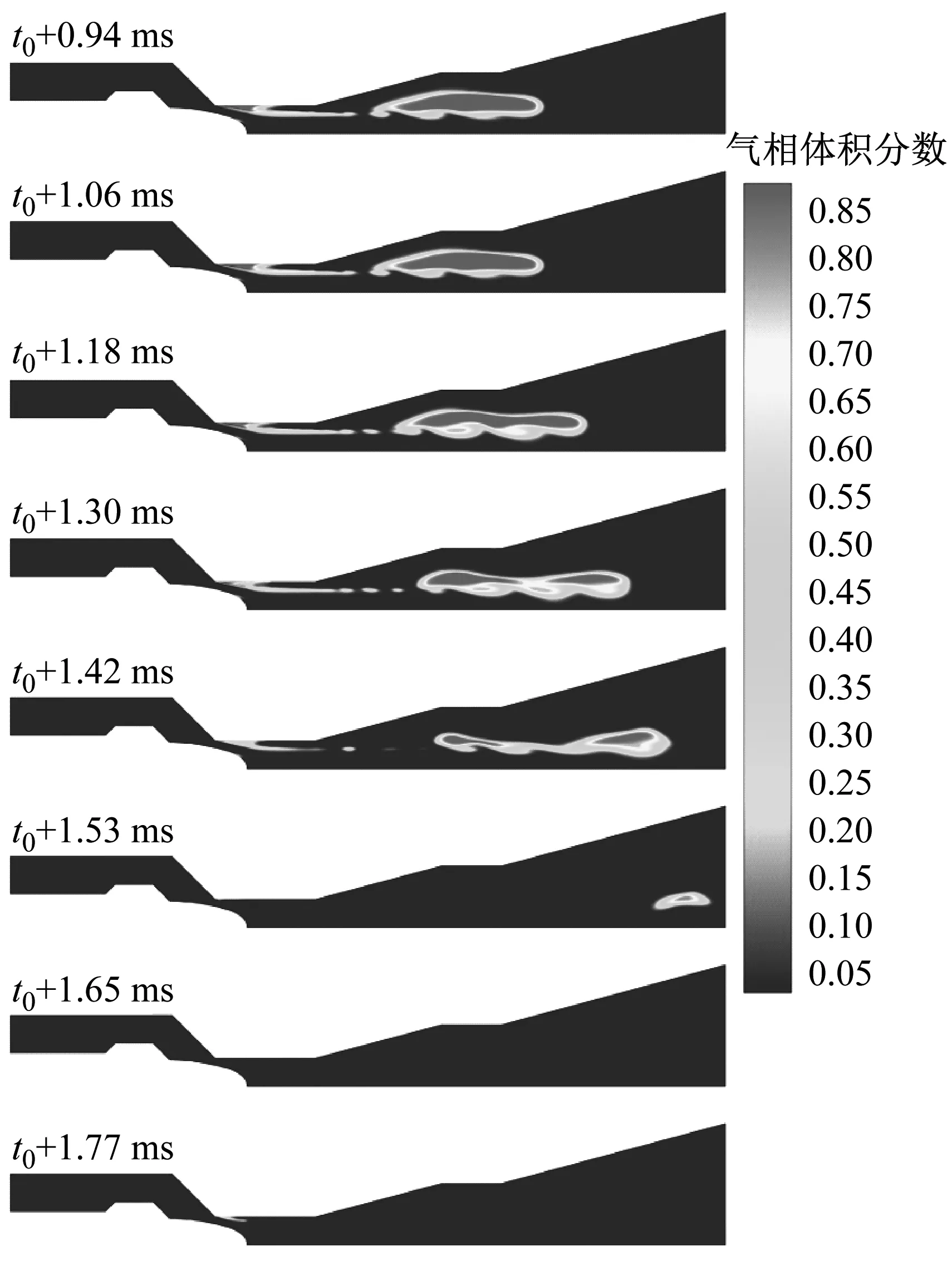
图3 空化结构演化典型过程Fig.3 Typical evolution process of cavitation flow
在时刻t0,调节阀阀口过流面积的减小使得流场内部压力降低,在阀口下游位置开始出现附着型空穴。在t0到t0+0.15 ms时,附着型空穴不断向下游发展;在t0+0.47 ms时,附着型空穴在尾部发生断裂,这是由反相射流导致的,同时在阀芯头部也有空穴产生,位于头部上表面。在t0+0.47 ms到t0+0.94 ms时,近壁面处的附着型空穴长度在逐渐减小,整个时间段均为附着型空穴断裂、脱落成游离型空穴的过程。在t0+0.94 ms时,游离型空穴完全脱落,且附着型空穴末端开始出现小的空穴脱落。在t0+0.47 ms到t0+1.06 ms时,游离型空穴随着主流向下游运动,其长宽方向尺度迅速变大,随着时间的推移,在t0+1.18 ms时,游离型空穴发展至最大形态,且在其表面有明显的波状波动产生。在t0+1.30 ms时,游离型空化逐步分裂为多个小尺度空穴,且在运动过程中逐渐溃灭,同时在t0+1.77 ms时进入下一个空化结构演化周期,空穴在阀口下游重新开始产生、发展。空穴脱落变化过程与陈广豪以及Qiu等[23]的试验研究结果一致。
2.2 空穴的增长和脱落
由于附着型和游离型空化在喉部及扩张段产生,为了具体说明空穴发展变化过程中其流场变化情况及其诱因,提取了图3中喉部和扩张段近壁面处流体的气相体积分数、压力、速度、压力梯度参量随时间变化情况,如图4所示。为更好的讨论1.25个周期内喉部以及扩张段中空化场的变化情况,我们取横坐标为无量纲量t/Tref,其中t为实际流动时间点,Tref为空化周期时间,此工况下为1.77 ms,纵坐标为无量纲量x/L2,其中x为横坐标值,L2为喉部长度。为分析空穴发展过程及形态变化规律,我们取气相体积分数值为0.1的等值线作为空穴与油液的边界线(见图4(a)中白实线)。从图4可知,在时刻a~时刻f整周期变化过程中,流场的气相体积分数、压力、速度和压力梯度一直处在变化中,但时刻a与时刻f两个时间点的各参数值基本相同,且对比0~0.25t/Tref与1.0~1.25t/Tref两时间段,各参数值及各参数变化趋势基本相同,具有明显的周期性。
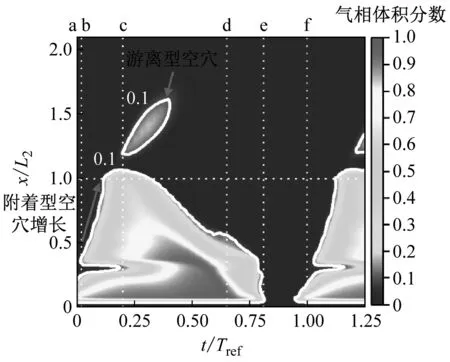
(a) 气体相积分数
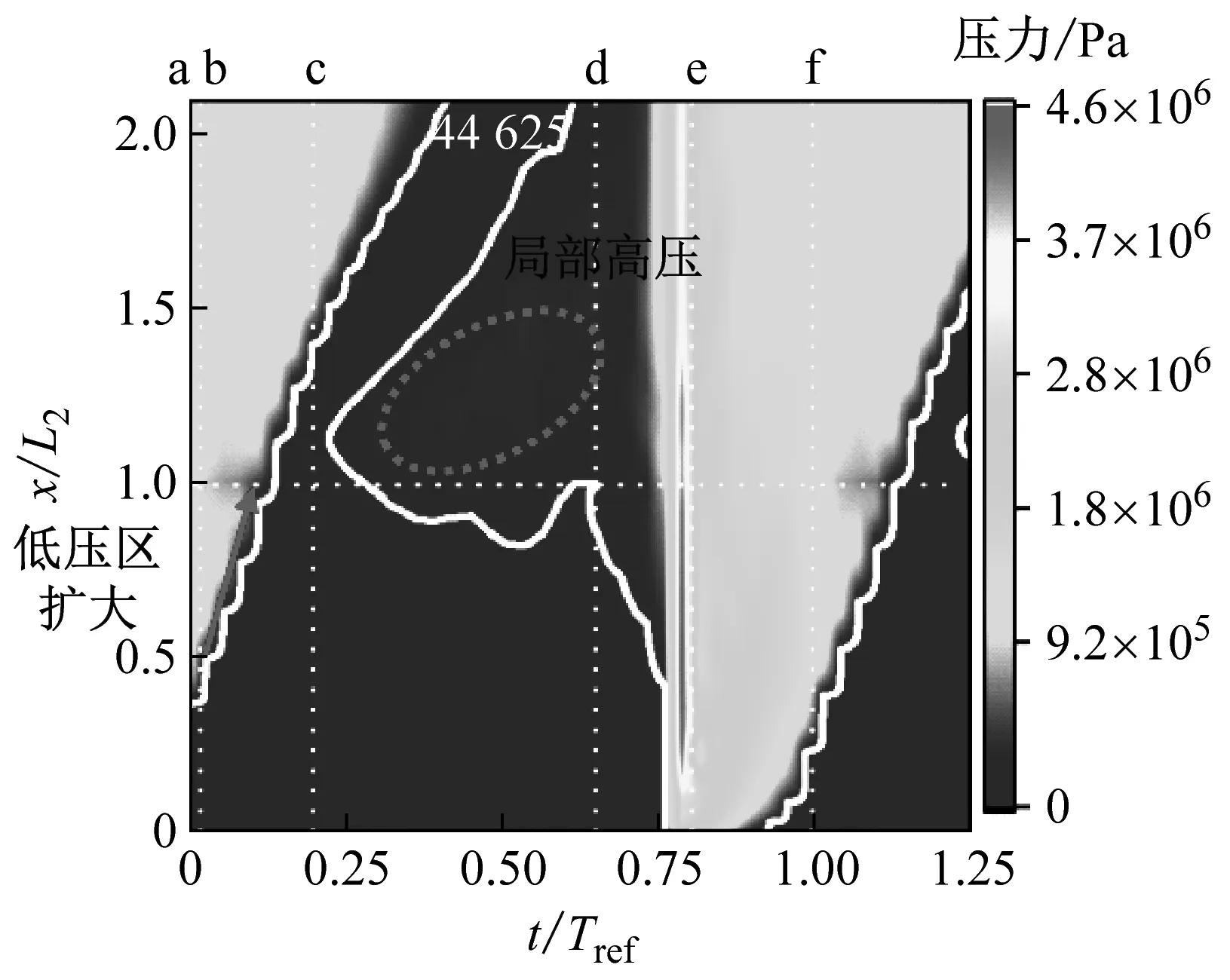
(b) 绝对压力

(c) 近壁面速度

(d) 近壁面压力梯度图4 空化周期中近壁面处各参数变化情况Fig.4 Variation of parameters near the wall during bubble oscillations
从图4(a)可知:在x/L2=0~x/L2=2.2区域可发现,在初始时刻附着型空穴产生,并在接下来的0.11t/Tref内不断增长,紧接着附着型空穴开始脱落。在接下来时间段,游离型空穴沿下游不断发展;同时,附着型空穴开始回缩,并在e时刻急剧消失。至f时刻,附着型空穴再次产生。
从图4(b)可知,在空化开始时刻a,未被空穴覆盖区域压力为1.0 MPa左右,接近设定的出口压力,被覆盖区域压力远低于1 MPa,低压区长度随着空穴增长而变大。在0.5t/Tref左右,x/L2=1.0~x/L2=1.5区域内空穴完成脱落,该区域压力逐渐回升,有局部高压出现,但压力仍低于1 MPa。在附着型空穴完全消失前,流道内压力激升,压力可达4.6 MPa,紧接着压力又回归至约1 MPa,直至下一周期空穴产生。
从图4(c)可知,在空穴发展变化过程中近壁面处一直有反向射流出现,且在空穴生长和脱落阶段,反向射流的边界一直随着空穴末端的位置变化而变化。在压力激升时刻,在喉部位置反向射流速度极大,可达34 m/s。结合图4(a)可知,在反向射流速度也急剧增加时,附着型空穴的回缩速度也在急剧增加,进一步说明反向射流是空穴发展变化的重要诱因。
图4(d)为逆压力梯度云图,每个点的逆压力梯度值由Px1-Px2(x1>x2)求得。结合图4(c)与图4(d)可知,观察区域内的逆压梯度主要出现在反向射流边界处,最大值约0.06 MPa。说明反向射流由逆压力梯度导致产生。在附着型空穴增长过程中,空穴覆盖的区域处于低压区,低压区域随着附着型空穴长度的增加在不断扩大。在空穴向下游发展过程中,气穴与油液交界面形成比较大的压力差,从而在近壁面处形成逆压梯度,导致在近壁面处有反向射流产生。
为进一步说明附着型空穴脱落原因,分析了三个典型时刻,流场内空化云图、速度云图、流线图,如图5所示。图5为不同时刻调节阀流道内流动状态。从图5可知,空穴形态不断变化,且漩涡伴随着空穴整个发展与脱落过程。

(a) t=0.01Tref空化云图
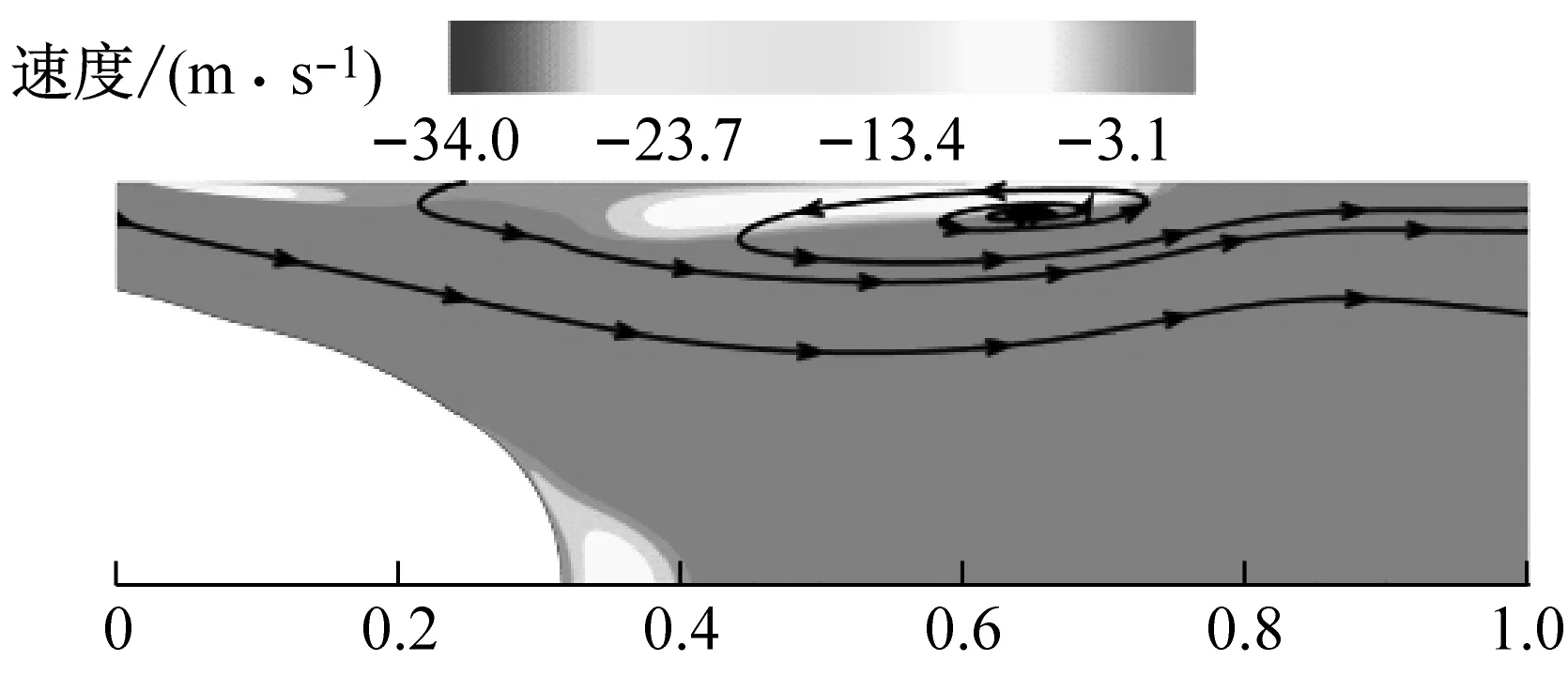
(b) t=0.01Tref速度云图

(c) t=0.02Tref空化云图

(d) t=0.02Tref速度云图

(e) t=0.65Tref空化云图
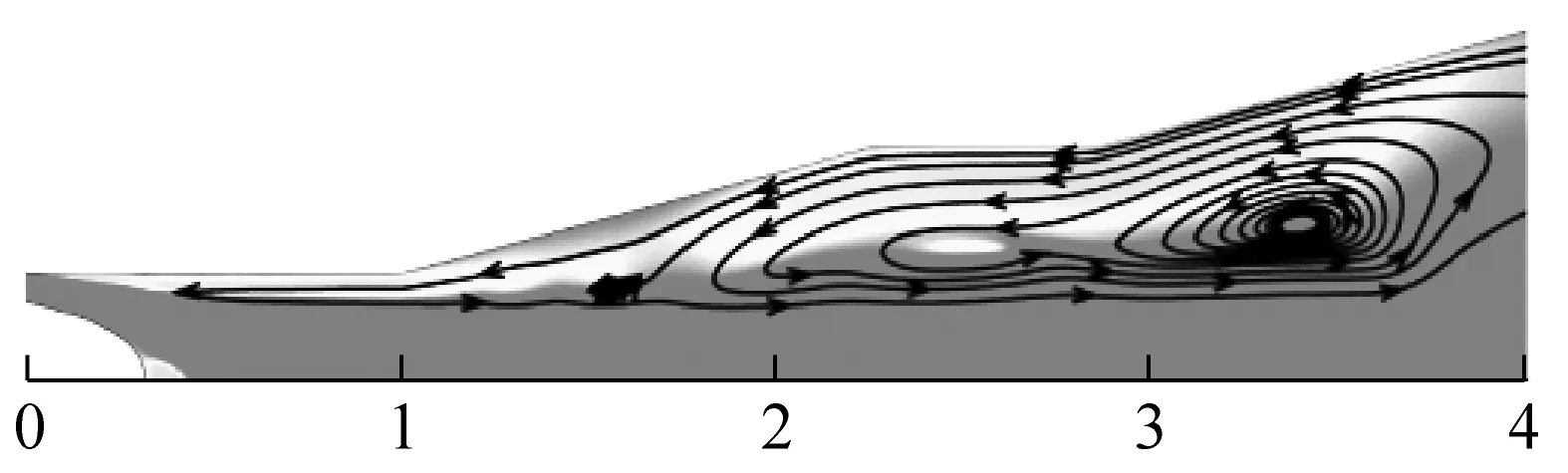
(f) t=0.65Tref速度云图图5 b、c、d时刻阀内流动状态Fig.5 Cavitation flow at the time b,c and d
b时刻附着型空穴正在缓慢增长,此时在附着型空化尾部与壁面间有反向射流产生,当主流遭遇反向射流时,一个小型湍流漩涡在紧贴壁面处形成,且此漩涡为逆时针方向。涡在空穴尾端产生,并伴随着附着型空穴向下游发展,但此时的涡较小,不足以形成足够的剪切力使附着型空穴脱落。此时空穴与液体交界面有明显的逆压梯度,这是反向射流形成的原因(见图4)。附着型空穴逐渐增长,涡也在逐渐变大,反向射流沿壁面向上游发展。由于流道x/L2=1处为喉部和扩张段交界处,流线在此处发生突变,反向射流在此处更容易形成涡(见图4(c)中方框)。随着空穴长度增长,空穴末端的涡也在逐渐变大,剪切力增强,且反向射流的流动介质以液相为主,因此会引起局部压强上升(见图4(b)中椭圆框),空穴中间产生局部高压,附着型空穴末端被涡剪切,促使其进一步断裂和脱落[24]。d时刻,游离型空穴完全脱离,并向下游发展,且此时反向射流继续沿喉部壁面向上游发展,促使附着型空穴逐渐回缩,直至其最终消失。同时,附着型空穴末端形成的涡对附着型空穴末端进行剪切,使其发生小的空穴脱落。
2.3 压力脉动分析
由上述讨论可知,在空穴发展变化过程中,压力场也在不断变化,空穴覆盖区域压力较低,空穴离开后压力逐渐回升,空穴溃灭时流道内产生剧烈的压力冲击。为进一步研究空穴形态变化过程中压力脉动特性,我们分别跟踪喉部、扩张段、一次和二次扩张段几何中心处压力变化情况。数值计算得到的10个空化周期内四个监测位置上的压力变化过程,如图6所示。图6(b)为典型的压力脉动时域信息图,图示表明:调节阀下游流道中空化呈现周期性演变趋势。由于调节阀内呈现非定常空化结构演化过程,各监测位置处压力的脉动数值明显不同,但是总体来看,四个位置都有比较大的压力波动,且有较强规律性。其中,1处由于受到附着型空穴前端长时间覆盖,受低压影响时间也最长,且附着型空穴前端较稳定,压力脉动也较小,因此1处长时间处于平缓低压区。2、3、4处由于受空穴覆盖时间逐渐变短,平缓低压区时长也逐渐减小。

(a) 四个监测位置

(b) 压力变化时域图

(c) 压力变化功率谱密度图

(d) 功率谱峰值频率变化图图6 四个监测位置压力信息Fig.6 Pressure at four monitoring points
图6(c)为对10周期各位置的压力信息进行功率谱密度谱求取的结果,从中可以发现,四个压力监测位置均存在频率在约565 Hz的主频峰,由附着型空穴的准周期生长、断裂和及其大尺度脱落引发;次级频率约为主导频率的各阶倍频,由游离型空穴非定常变化及附着型空穴末端脱落的小气泡引起。分析流道内不同截面的压力脉动信息可知,不同截面上的平均压力变化具有相同的主导频率,且该频率与附着型空穴准周期生长、断裂和大尺度脱落频率基本一致。图6(d)为功率谱峰值频率变化图,对应空穴不同形状,峰值频率呈现减小的趋势,但是测点2位于扩张段,为空穴形态变化最剧烈的地方,所以功率谱峰值变化比较大.此外,在十个周期的空化变化中,1、2、3处最高压力可达6 MPa以上,而4处最高压力远小于这三个位置,约为2.5 MPa。此处可能是因为二次扩张段的存在有利于减轻空化引发的压力脉动对下游的影响,对工程应用中调节阀的优化设计和稳定运行有实际的指导意义。
本文引入脉冲因子作为用来检测信号中有无冲击的指标,脉冲因子表达式为
I=(Pmax-Pmin)/Parv
(1)
(2)
式中:Pi为时域上第i个时间点的压力值;采样时间间隔为0.01 ms;Pmax为压力最大值;Pmin为压力最小值。
图7呈现的是在10周期非定常变化过程中,整个流道内各截面压力值的脉冲因子。可以发现,脉冲因子最大值在x/L2=0.2处,即流道的节流口处,说明此处压力脉冲最大。可知空穴变化过程中,流场内受空化影响最大、受冲击最强位置为x/L2=0.2截面处,因此节流口也将是受到压力冲击最严重的地方、最易形成空蚀的地方,应加强对节流口处的保护。

图7 空化十个周期各截面压力脉冲因子Fig.7 Pressure pulse riskfactor at each section in ten cavitation oscillationcycles
3 结 论
基于对调节阀内数值模拟结果的分析,结论如下:
(1) 调节阀内空穴的发展变化呈现明显的准周期性过程,包括附着型空穴生长,附着型空穴断裂、脱落,以及游离型空穴的增长和溃灭。
(2) 附着型空穴尾部近壁面处产生的反向射流是引发其断裂的直接原因。在空穴形成后,空穴与液体交界面会形成压力梯度,进而形成反向射流。反向射流与主流相切形成的涡一直剪切附着型空穴,使其断裂、脱落,涡一直伴随着空穴变化过程。反向射流中液相为主要流动介质,会导致局部压力上升,填充部分气体空腔,这是引起空穴断裂的直接原因。
(3) 附着型空穴生长时,空穴覆盖区域压力变低,且附着型空穴前端较稳定,压力脉动也较小,其尾部压力波动较大。伴随着反向射流的发展,附着型空穴断裂、脱落形成游离型空穴,整个过程中压力脉动变得复杂,原本被空穴覆盖区域的压力开始逐渐回升;空穴大面积溃灭时,流道内会有较大压力冲击产生,其值远高于出口压力,加速了残存空穴的溃灭过程。阀内不同截面上的平均压力变化具有相同的主导频率,且该频率与附着型空穴准周期生长、断裂及大尺度脱落频率基本一致。

