轴颈倾斜下船用复合衬层艉轴承混合润滑特性分析及结构优化

吕芳蕊， 饶柱石， 王 珏

(1.河海大学 机电工程学院，江苏 常州 213022； 2.上海交通大学 机械系统与振动国家重点实验室，上海 200240)

船用艉轴承常采用自然水作为润滑剂，润滑剂的低黏和低速重载工况常使艉轴承处于混合润滑状态；轴承承载面通常为非金属材料以提高耐磨性减小振动，因此轴瓦存在较大的弹性变形；同时，螺旋桨的重力作用常使轴颈发生倾斜。船用艉轴承的特殊性引起了许多学者的兴趣[1-4]。

一些学者致力于改进轴承分析模型。He等[5]基于Patir等[6]提出的平均雷诺方程建立了考虑轴颈挠曲的船用艉轴承数值计算模型。Wang等[7-8]建立了热弹流混合润滑模型，其中轴承变形采用影响系数法计算。目前已有水润滑轴承的研究[9]采用影响系数法计算轴承变形。水润滑艉轴承常设计有轴向导水槽，以利于散热和排沙，导水槽对轴承性能影响显著。Mallya等[10-11]分析了开槽角度分别为18°和36°的轴承，认为轴颈倾斜和紊流均提高了开槽轴承的承载能力。Majumdar等[12]的研究发现当轴向槽具有较小的螺旋角时，轴承承载能力有所提高。Xiang等[13]分析了开槽轴承的磨损特性，提出了微沟槽水润滑轴承的动态磨损模型。Zhou等[14]研究了不同形状的沟槽对水润滑轴承摩擦因数的影响，并指出螺旋槽轴承较直槽轴承具有更好的摩擦学特性。螺旋桨的重力作用常使艉轴承的轴颈发生倾斜。Sun等[15-16]的研究表明，轴颈倾斜对轴承性能的影响十分显著。Jang等[17]提出了轴颈倾斜下磨损对发动机轴承影响的评估模型，并指出轴颈倾斜增大了最大磨损深度，且磨损深度随表面粗糙度的增大而增大。Xiang等[18]分析了轴颈倾斜下三种不同沟槽结构(直槽、螺旋槽和人字槽)轴承的瞬态润滑性能，其研究表明，考虑轴向运动时轴承承载能力对轴颈倾角更为敏感。

为改善轴承润滑性能，许多学者致力于优化轴承结构。Hirani等[19]提出了一种优化方法，可设计轴承参数轴承使润滑油流量和功率损失达到最小。Chu[20]提出了滑动轴承的逆设计方法。Ouyang等[21]基于理论和实验指出，具有阻尼结构的水润滑轴承动态特性显著改善。近年来大量研究表明适当应用表面织构可改善摩擦特性，表面织构技术在轴承中也逐渐得到应用[22-25]。Meng等[26-27]分析了表面织构对轴承摩擦学性能的影响，其研究结果表明，复合凹坑织构可提高滑动轴承的承载能力、减小摩擦，并降低轴承的平均噪声声功率级。上述研究可在一定程度上优化轴承特性，但对改善轴颈倾斜下水润滑轴承的润滑性能效果不明显。由于螺旋桨的重力作用，船用艉轴承的轴颈极易发生倾斜，严重恶化了轴承性能，因此有必要考虑轴颈倾斜对艉轴承进行设计。

在过去几十年，橡胶是水润滑艉轴承最常用的材料之一；但橡胶衬层摩擦噪声大、易于发生振动异常。目前，赛龙等高分子材料(后文简称高分子材料)常被用来代替橡胶，用作水润滑轴承衬层。高分子材料具有低摩擦、高承载的特点，然而，其弹性模量远大于橡胶，因而其衬层变形远小于橡胶衬层。当轴颈倾斜时，高分子轴承的轴颈和轴瓦更易发生摩擦，润滑水膜的建立更困难。

为改善轴颈倾斜下水润滑艉轴承的润滑性能，本文提出了一种采用多层复合衬层的轴承设计方法。以高分子材料作为承载表面，在高分子承载层与金属外壳之间加入橡胶层，橡胶层为等厚或非等厚结构。在此基础上建立复合衬层水润滑轴承的混合润滑模型，并分析单一衬层结构、复合衬层结构下的轴承性能；针对非等厚复合衬层结构分析最优橡胶层厚的影响因素，并总结最优橡胶层厚的拟合公式，以便应用于轴承设计。

1 轴颈倾斜下复合衬层水润滑轴承模型

1.1 几何模型

润滑剂低黏度及低速重载工况导致水润滑艉轴承常处于混合润滑状态。为提高耐磨性和降低振动，水润滑艉轴承多采用非金属衬层。赛龙高分子材料(后简称高分子材料)是船用水润滑艉轴承常用材料之一。图1为典型高分子轴承的结构示意图，轴承由高分子衬层和金属外壳组成。螺旋桨的重力作用常导致轴颈在竖直方向倾斜(如图1所示)，从而恶化了轴承润滑性能。为改善润滑特性，本文提出了一种复合衬层轴承结构，如图2(b)所示，轴承由高分子层、橡胶层和金属层组成。高分子层用作承载面，橡胶层用作中间层，以增大轴承的变形。橡胶层沿轴向可为等厚的，也可为非等厚的。

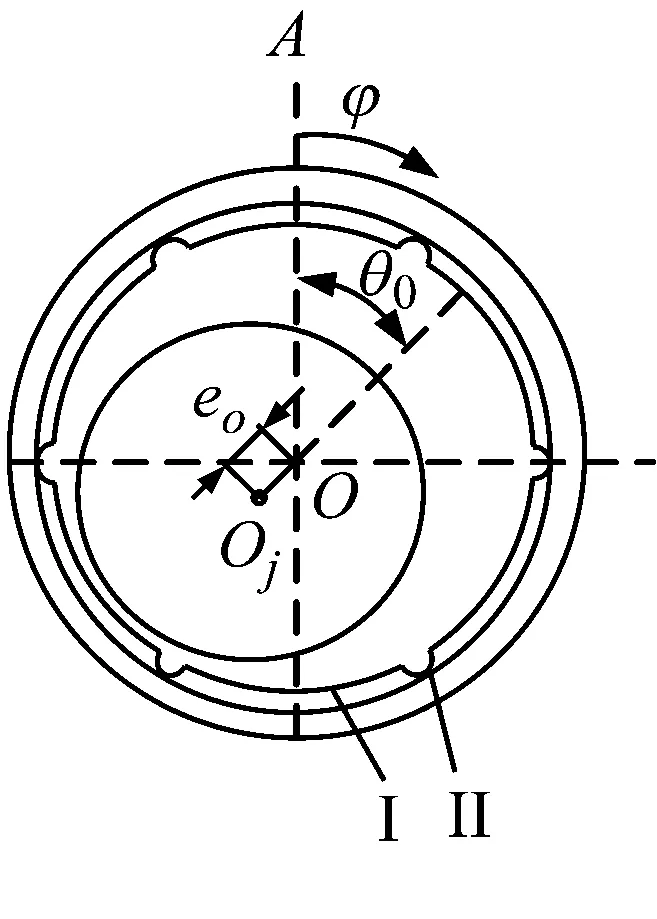
图1 轴颈倾斜下高分子水润滑轴承结构示意图Fig.1 Schematic diagram of a polymer water-lubricated bearing with journal misalignment

(a) 普通高分子轴承

(b) 复合衬层轴承图2 不同衬层结构的轴承Fig.2 Bearings with different liner structures

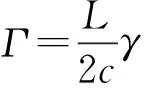
(1)

式中:ε和θ分别为轴颈下沉端面的偏心率和偏位角(下文分别简称偏心率和偏位角);z为轴向坐标。

考虑轴颈倾斜及轴向槽的轴承液膜厚度表达式为

(2)

式中：Δh为水槽中节点的深度;u为轴瓦变形。变形量可通过影响系数法求解

(3)

式中：G(φj,zk,φξ,zη)为影响系数矩阵，其中的数据为由作用在附近某个节点上的单位力引起的节点位移；w(φξ,zη)是节点力。影响系数矩阵可通过有限元法得到，对于复合衬层轴承，有限元模型包括三层，即高分子层、橡胶层和金属层。

需要注意的是，式(2)中的h是光滑表面假设下的液膜厚度，即名义膜厚。如图3所示，考虑表面粗糙度时，当地膜厚hT与名义膜厚h的关系如下

图3 粗糙表面间的液膜厚度Fig.3 Thickness of the film between rough surfaces

1.2 控制方程

hT=h+δ1+δ2

(4)

处于稳态工况的滑动轴承，混合润滑状态下水膜压力可通过平均雷诺方程求解

(5)

水膜承载力可通过下式得到

(6)

式中，Fliqξ和Fliqη分别为液膜力在水平方向和竖直方向的分力。

等效微凸体接触压力可利用Greenwood-Tripp模型[28]求得

(7)

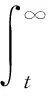
粗糙峰接触力的水平和垂直分量分别为

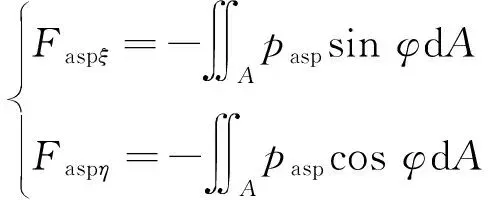
(8)

摩擦力可由下式求得

Ff=Ffliq+Ffasp

(9)

1.3 数值计算流程

图4为轴承数值计算流程图。首先利用有限元法得到影响系数矩阵G(φj,zk,φξ,zη)；首次迭代时，将膜厚方程式(2)中的轴瓦变形u设置为零，可得膜厚h；将膜厚h代入平均雷诺方程式(5)求解水膜压力，并将膜厚h代入式(7)求解粗糙峰接触压力；将求解得到的压力转化为节点力代入式(3)计算轴瓦变形u；将变形u代入膜厚方程式(2)获得新的膜厚h；从而可再次求得新的水膜压力和粗糙峰接触压力。反复迭代，直到满足收敛条件，再通过式(6)和式(8)计算水膜承载力和粗糙峰接触力。

图4 计算流程图Fig.4 Flow chart of numerical calculation procedure

2 不同结构轴承性能分析

本节以三个轴承为例分析不同结构轴承的性能。轴承I的衬层为5 mm高分子材料，轴承II为等厚复合衬层(由5 mm聚合物层和10 mm橡胶层构成)，轴承III为10 mm橡胶衬层。轴承其它参数如表1所示。

表1 轴承参数Tab.1 Bearings’ parameters

2.1 轴承液膜压力分析

图5和图6为轴承I和轴承II的水膜平均压力分布。如图所示，当轴颈无倾斜时，轴承的液膜压力在轴向对称；当轴颈倾斜时，峰值压力向轴颈下沉端移动，最大液膜压力显著增加。由此可知，当轴颈倾斜时，下沉端局部承担了大部分载荷。对比图5(b)和图6(b)可见，当轴颈倾斜时，复合衬层轴承的最大平均液膜压力显著降低，说明复合衬层显著改善了压力分布的均匀性，增大了轴向实际承载面积。

(a) 轴颈倾角0 mrad

(b) 轴颈倾角0.1 mrad图5 轴承I液膜平均压力分布Fig.5 Mean hydrodynamic pressure distribution of bearing I

(a) 轴颈倾角0 mrad

(b) 轴颈倾角0.1 mrad图6 轴承II液膜平均压力分布Fig.6 Mean hydrodynamic pressure distribution of Bearing II

2.2 轴承液膜厚度分析

图7为不同倾角下轴承的名义液膜厚度，可见当轴颈倾斜且轴颈转速较低时，轴承II的最小名义液膜厚度最大，这是因为复合衬层增大了轴承在轴向的实际承载面积。倾角越大，复合衬层对最小膜厚的提升作用月明显。当转速升高时，由于复合衬层轴承存在较大的弹性变形，其最小膜厚的增幅小于高分子轴承。

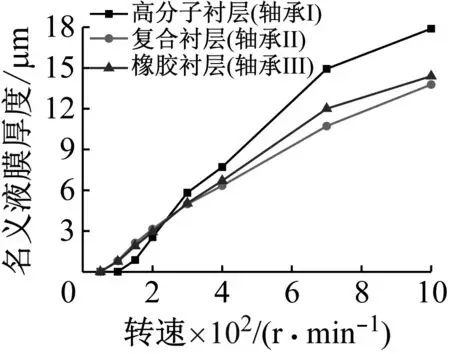
(a) 轴颈倾角0.05 mrad

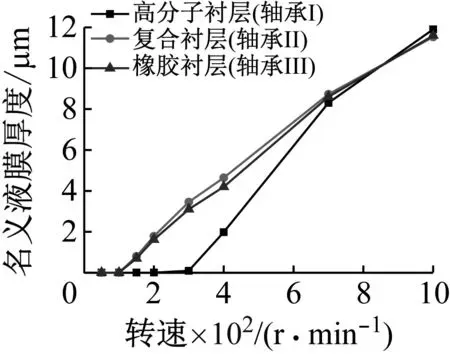
(b) 轴颈倾角0.1 mrad图7 轴承名义膜厚随转速的变化关系图Fig.7 Nominal film thickness versus rotational speed

2.3 摩擦因数分析

图8为不同倾角下轴承的摩擦因数。三轴承转速较低时摩擦因数均较大，表明轴承处于混合润滑状态。随着转速的上升，三轴承的摩擦因数先减小后增大。当轴颈倾斜且轴颈转速较低时，轴承II(复合衬层轴承)的摩擦因数最低。这是因为复合衬层增大了轴承在轴向的实际承载面积，增大最小名义厚度，从而减小了粗糙峰接触摩擦力。在工程中，摩擦因数最小处通常被视为轴承由混合润滑向流体动压润滑过渡的转折点，可见复合衬层降低了轴承由混合润滑状态过渡到纯流体动力润滑状态时所对应的转速。对比轴承II与轴承III，可以发现当轴颈倾斜的轴承处于混合润滑状态时，轴承II的摩擦因数较低，这是因为高分子复合材料的摩擦因数低于橡胶材料。

(a) 轴颈倾角0.05 mrad

(b) 轴颈倾角0.1 mrad图8 轴承摩擦因数随转速的变化关系图Fig.8 Friction coefficient versus rotational speed

3 非等厚复合衬层轴承结构优化

由前文的分析可知，轴颈倾斜时等厚复合衬层结构可显著改善轴承性能，但其液膜压力在轴向分布仍不均匀，本节针对含非等厚橡胶层的复合衬层轴承进行研究，以压力沿轴向分布均匀为目标对橡胶层厚度进行优化，并分析最优橡胶层厚与轴承参数的关系，为轴承设计提供参考。

3.1 压力不均匀因子及最优橡胶层厚

本文中含非等厚橡胶层的复合衬层轴承如图9所示，在径向剖面内橡胶层为三角形，轴颈下沉端橡胶层最厚，本文将最大橡胶层厚度简称为橡胶层厚。

图9 含非等厚橡胶层的优化轴承结构示意图Fig.9 The optimum bearing with triangle rubber layer

由第2章的分析可知，轴颈倾斜时轴承性能恶化的原因是轴承压力分布不均，定义压力不均匀因子以表征压力分布的不均匀程度

(10)

PF=f(ε,γ,L/D,D,φ,thc,a,β,n)

(11)

式中：thc为轴颈下沉端面处的橡胶层厚，也即橡胶层的最大厚度，后文简称橡胶层厚；a为高分子衬层厚度；β为承载区的包角。由式(11)可知，PF为大于或等于0的数值，PF越小反映压力分布越均匀，因此当PF达到最小时所对应的橡胶层厚即为最优橡胶层厚。

对不同橡胶层厚度的轴承(其它参数见表2)进行分析，得到液膜压力分布如图10所示。可见，当无橡胶层时，压力分布不均，此时PF为0.941。随着橡胶层厚度增大，压力分布趋向于均匀，压力峰由下沉端向轴向中分面移动，PF减小，当橡胶层厚为15 mm时，PF达到最小值0.167。此后，随着橡胶层厚继续增大，压力分布再次趋向不均匀，液膜最高压力向轴颈上翘端移动，PF增大，当橡胶层厚为28 mm时，压力不均匀因子PF为0.235。

表2 含非等厚橡胶层的轴承参数Tab.2 Parameters of the bearing with non-uniform thickness rubber layer

(a) 橡胶层厚0 mm

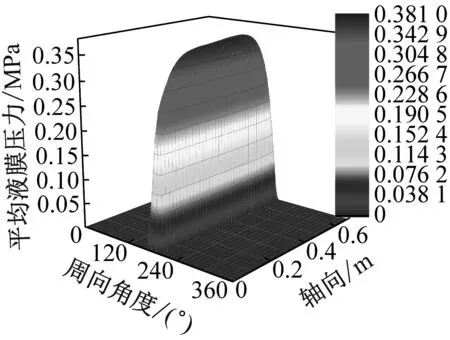
(b) 橡胶层厚15 mm

(c) 橡胶层厚28 mm图10 不同橡胶层厚度下轴承压力分布Fig.10 The pressure distributions of the bearing versus rubber layer thicknesses

由该算例可见，压力不均匀因子PF可表征液膜压力分布的不均匀程度，对于轴颈倾斜的轴承，存在一个最优橡胶层厚使PF达到最小。由式(11)可知，最优橡胶层厚thc0是轴承结构参数及运行参数的函数

thc0=g(ε,γ,L/D,φ,a,n,β,D)

(12)

3.2 最优橡胶层厚的影响因素分析

下面分析最优橡胶层厚随轴承参数的变化关系。

图11为不同偏心率下最优橡胶层厚随轴颈倾角的变化关系图。当偏心率一定时，轴颈倾角增大导致压力分布不均匀程度增加，因而最优橡胶层厚也相应增大。类似地，当倾角一定时，偏心率增大使压力分布均匀程度有所改善，因而最优橡胶层厚也相应减小。

图11 不同偏心率下最优橡胶层厚随倾角的变化Fig.11 Optimal rubber layer thicknesses versus misalignment angles and eccentricity ratios

图12为不同间隙比与不同轴颈倾角下的最优橡胶层厚，偏心率为1.05。偏心率与轴颈倾角一定时，最优橡胶层厚随间隙比的增大而减小。图13为不同轴颈倾角下最优橡胶层厚随转速的变化关系图，偏心率为1.05。偏心率及倾角一定时，最优橡胶层厚随转速的升高而下降。

图12 不同间隙比下最优橡胶层厚随倾角的变化Fig.12 Optimal rubber layer thicknesses versus misalignment angles and clearance ratios

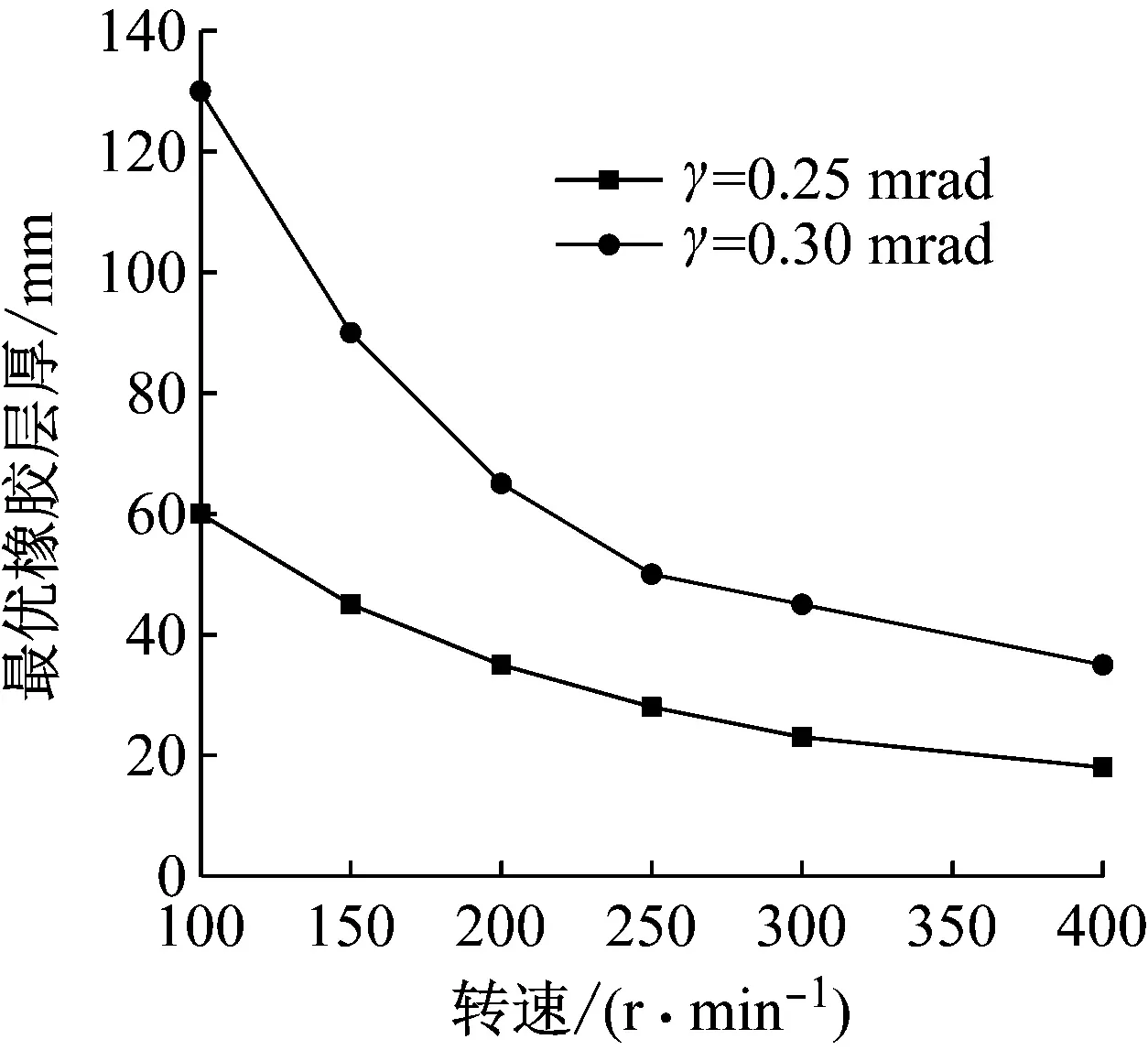
图13 不同倾角下最优橡胶层厚随转速的变化Fig.13 Optimal rubber layer thicknesses versus misalignment angles and speeds

表3为不同长径比下的最优橡胶层厚。其它参数一定时，长径比与倾角的乘积相同的轴承其最优橡胶层厚近似相等。如偏心率0.999时，长径比1倾角0.15 mrad的轴承与长径比3倾角0.05 mrad的轴承最优橡胶层厚近似相等。原因如下：根据轴颈倾斜的轴承结构示意图(图1)，长径比1倾角为0.15 mrad的轴承，其轴颈下沉端的膜厚与上翘端膜厚的差值与长径比3倾角为0.05 mrad的轴承近似相等，因此两种情况下轴承的最优橡胶层厚也近似相等。

表3 长径比对最优橡胶层厚的影响Tab.3 The influence of length-diameter ratio on optimal rubber layer thickness

由表4可知，当偏心率一定时，若高分子层厚处于10～50 mm的范围内，高分子层厚的影响较小，基本可忽略。类似的，根据表5，偏心率一定时瓦块包角的影响也较小，基本可忽略。

表4 赛龙层厚对最优橡胶层厚的影响Tab.4 The influence of liner thicknesse on optimal rubber layer thickness

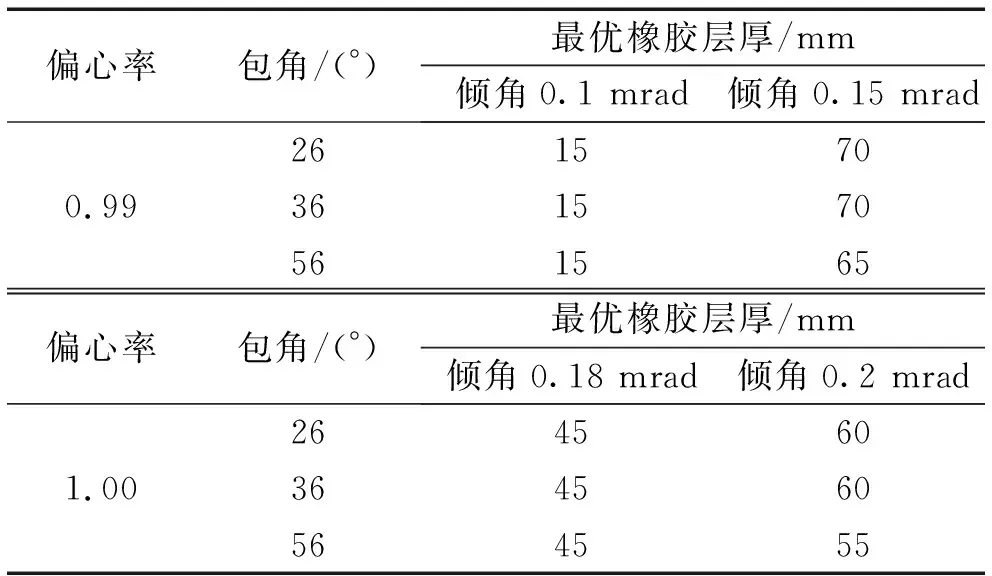
表5 包角对最优橡胶层厚的影响Tab.5 The influence of wrapping angle on optimal rubber layer thickness

3.3 最优橡胶层厚拟合公式

通过大量计算，得到了最优橡胶层厚随各参数变化的变化关系，通过拟合曲线得到最优橡胶层厚可近似表达为

(13)

考虑进行轴承设计时通常偏心率非已知量，而是需先根据比压进行初步设计，因此分析了最优橡胶层厚与比压的关系，如图14所示，最优橡胶层厚随比压的增大而减小，变化曲线近似为双曲线函数。其中轴颈倾角0.2 mrad下，最优橡胶层厚随比压的变化关系可近似表达为

图14 不同倾角下最优橡胶层厚随比压的变化Fig.14 Optimal rubber layer thicknesses versus misalignment angles and specific pressures

(14)

轴颈倾角0.35 mrad下最优橡胶层厚随比压的变化关系可拟合为

(15)

得到的拟合曲线如图15所示，可见误差均较小。

(a) 轴颈倾角0.20 mrad

(b) 轴颈倾角0.35 mrad图15 最优橡胶层厚随比压变化的拟合曲线Fig.15 Fitting curve of optimal rubber layer thicknesses versus specific pressures

考虑长径比、包角、间隙比、转速、高分子层厚等因素，总结得到以比压为自变量的最优橡胶层厚公式为

(16)

式(16)可用于轴颈倾斜下复合衬层轴承的设计计算，公式适用范围为：长径比为1～6，轴颈倾角为0～0.4 mrad，轴承直径为400～700 mm，间隙比为1.8‰～3.2‰，轴承正下方单个承载区的包角为26°～120°。该范围涵盖了船用艉轴承常用的结构参数。

4 结 论

(1) 轴颈倾斜常导致船用艉轴承的润滑性能严重恶化。为改善轴颈倾斜下轴承的润滑性能，提出了一种采用复合衬层的轴承设计方法。以高分子材料作为承载表面，在高分子承载层与金属外壳之间加入橡胶层，橡胶层为等厚或非等厚结构。在此基础上建立了复合衬层水润滑轴承的混合润滑模型，分析了单一衬层结构及复合衬层结构下的轴承性能。

(2) 分析结果表明，当轴颈倾斜时，大部分外载荷由轴承轴向局部承担。轴颈倾斜下轴承处于混合润滑时，与高分子衬层轴承相比，复合衬层改善了压力分布、显著增加了轴向实际承载面积、增大了最小名义液膜厚度、减小了粗糙峰接触力，从而减小了摩擦，并降低了混合润滑状态过渡到流体动力润滑状态时的转速。与橡胶衬层相比，复合衬层降低了轴承混合润滑状态下的摩擦因数。

(3) 对非等厚复合衬层轴承的最优橡胶层厚的影响因素进行了分析，总结得到最优橡胶层厚的拟合公式，并给出了公式的适用范围，公式形式简洁，便于应用于轴承设计计算。