不同桥跨对中低速磁浮列车-简支梁系统竖向耦合振动影响机理研究

李小珍, 王渝文, 胡启凯, 王党雄

(1.西南交通大学 土木工程学院，成都 610031； 2.西北工业大学 力学与土木建筑学院，西安 710072)

中低速磁浮列车作为极具竞争力的交通工具，其具有安全性高、经济性好、噪声低、爬坡能力强、转弯半径小等优点[1-2]，在未来城市交通中具有良好的发展前景[3]。

中低速磁浮列车通过主动调节电磁悬浮力使车体保持在额定悬浮间隙(8～10 mm)附近，从而实现平稳运行[4]。当磁浮列车在桥梁上运行时，桥梁会产生形变，从而改变悬浮间隙，影响电磁悬浮力，导致磁浮列车-桥梁系统耦合振动，影响磁浮列车的平稳运行[5-6]。国内外学者针对磁浮列车-桥梁系统耦合振动进行了诸多研究。文献[7]建立了5自由度磁浮车辆模型，探讨了考虑与不考虑耦合振动时，车体及桥梁结构动力响应的差异。文献[8]建立了10自由度的TR06磁浮列车模型，将悬浮控制系统简化为线性弹簧阻尼系统，讨论了在随机不平顺激励下磁浮列车-高架桥系统竖向耦合振动。文献[9-10]研究分别在中低速和高速磁浮列车作用下，桥梁和车辆的动力响应，并通过现场试验进行验证。文献[11]建立了高速磁浮车辆-桥梁系统的空间耦合振动模型，桥梁采用有限元模型，探讨了在有无随机不平顺激扰时系统各动力响应的频谱分布规律。文献[12-14]建立了磁浮列车-桥梁系统耦合振动模型，分析了桥梁刚度、材料和结构形式对磁浮列车-桥梁系统动力响应的影响。文献[15-16]探究了风荷载对磁浮列车-桥梁系统耦合振动的影响。

简支梁作为磁浮线路中不可或缺的结构，其跨度会随着地形和外界影响因素而改变。磁浮列车在不同跨径的桥梁结构上运行时，会改变桥梁结构变形的波长和幅值，从而使磁浮车桥耦合振动特征产生差异，但目前磁浮线路中多采用25 m简支梁，而对其它跨径下的磁浮车桥系统耦合振动特性的研究较少，使得目前工程中不能灵活地根据实际情况而选择简支梁的跨径。本文基于前人研究的基础，考虑PID(proportion intergration differentiation)主动悬浮控制系统，基于模态叠加法，建立中低速磁浮列车-简支梁系统竖向耦合振动分析模型，对不同跨径下中低速磁浮列车简支梁系统耦合振动特性及机理进行深入研究。本文的研究以期为后续在保证磁浮列车安全平稳运行前提下，灵活选择不同跨径的磁浮线路简支梁提供理论支撑和借鉴。

1 中低速磁浮列车-桥梁耦合系统理论模型

1.1 中低速磁浮车辆模型

本文以EMS 5模块中低速磁浮列车为研究对象。磁浮列车主要由车体、空气弹簧、悬浮架和电磁铁组成，车体通过空气弹簧与悬浮架连接。由于建立精细的磁浮列车模型较困难，因此，需要对磁浮列车模型进行一定简化：车体和悬浮架简化为刚体，空气弹簧采用线性弹簧阻尼单元，电磁铁产生的悬浮力简化为集中力，EMS 5模块中低速磁浮列车简化示意图，如图1所示。

图1 5模块中低速磁浮列车简化示意图Fig.1 Simplified schematic diagram of five-module low and medium speed maglev train

作用在车体和悬浮架上的荷载分布示意图，如图2所示。考虑磁浮车体和悬浮架的竖向和俯仰自由度，分别用Zc、βc、Zs和βs表示，其中Fij(i=1～5，j=1,2)表示第i架第j次弹簧阻尼力；fin(i=1～5，n=1～4)表示第i个悬架上的第n个悬架力。

图2 荷载示意图Fig.2 Load diagram

根据D’Alembert原理，建立车辆运动方程，如式(1)所示

(1)

1.2 基于PID悬浮控制系统模型

Shi等提出了基于位移-速度-加速度反馈的主动悬浮控制模型，其主动悬浮控制系统的电流方程为

(2)

根据电磁悬浮力与悬浮间隙和电流的关系，最终输出电磁悬浮力f(t)如式(3)所示

f(t)=

(3)

式中：Kf为电磁比例因子；i0和c0为额定电流和额定悬浮间隙。

1.3 不同跨度桥梁模型

桥梁模型采用模态叠加法求解[17]。在外荷载的作用下，桥梁的运动微分方程为

(4)

式中：m为桥梁的质量矩阵;c为阻尼矩阵；k为刚度矩阵;f为作用于桥梁的外荷载列向量，即电磁悬浮力列向量。

利用模态叠加法，桥梁的位移表示为

(5)

式中：φn为桥梁的第n阶振型;qn为桥梁的第n阶广义坐标。

将式(5)代入式(4)中，根据振型的正交性，可将桥梁的运动微分方程解耦成

(6)

从式(6)可知，只需求得桥梁的自振频率以及作用于桥梁上的广义外荷载值，就可求解桥梁的运动微分方程，使桥梁广义动力方程的求解变得简单，然后通过振型叠加法，求得桥梁的各动力响应。

1.4 耦合振动模型求解

将式(1)与式(6)联立，可构成磁浮列车-桥梁耦合系统动力方程，如式(5)所示。电磁力作为联系车辆系统和桥梁系统的媒介，可通过式(7)求解。

(7)

式(7)为大型非线性时变系统的动力方程，利用解析法难以求解，需要采用基于Newmark-β积分的分离迭代法求解，具体可参考文献[18]中的求解流程。

2 计算参数与模型验证

2.1 计算参数

选取某中低速磁浮试验线中的25 m、30 m和35 m跨径预应力混凝土简支梁为研究对象，其跨中截面尺寸如图3所示。各个简支梁均采用双线箱梁，线间距4.4 m，两个箱梁之间通过横隔板连接，采用C50混凝土，单线二期恒载为22 kN/m。计算参数如表1所示。

图3 不同跨径简支梁跨中截面尺寸(cm)Fig.3 Cross section of the simply supported beam of different spans at midspan(cm)

表1 计算参数Tab.1 Calculation parameters

目前有关中低速磁浮线路不平顺的理论与实测研究较少。本文采用以往文献中推荐的轨道不平顺模型，功率谱密度函数如下

(8)

式中：Ω为空间波数；n为频率特征参数(取值为1.5～4.5)；Ar为表面粗糙度系数。本文中，n=2，对于竖向不平顺，Ar=1.5×10-7m。采取三角级数法将功率谱函数变换为轨道不平顺时域样本，如图4所示。从图4可知，左侧和右侧轨道不平顺的幅值约为±2 mm，波长为0.1～100 mm。

(b) 右侧轨道图4 轨道不平顺谱Fig.4 Random irregularity of track

2.2 模型验证

为验证中低速磁浮列车-桥梁耦合理论模型的可靠性，以长沙磁浮线路中典型的25 m简支梁作为验证对象。图5所示为25 t+25 t+25 t磁浮列车以速度80 km/h在25 m简支梁上运行时的仿真与实测曲线对比图。

(a) 简支梁跨中动挠度

(b) 简支梁跨中竖向加速度图5 25 m简支梁跨中试验与仿真对比图Fig.5 Experimental and simulation comparison diagram of 25 m simply supported beam at midspan

可以看出，磁浮列车在25 m简支梁上运行，桥梁跨中动力响应的仿真值与实测值均较吻和，这充分证明了本文建立的磁浮车桥耦合振动理论模型的正确性。

2.3 模态分析

采用有限元软件ANSYS分别建立25 m、30 m和35 m跨径简支梁有限元模型，25 m简支梁有限元模型如图6所示。不同跨径简支梁的一阶竖弯模态图如图7所示。从图7可知，简支梁的一阶正对称竖弯频率随着跨径的增大逐渐减小。

图6 25 m简支梁有限元模型Fig.6 FEA model of 25 m simply supported beam

(a) 25 m, f=4.83 Hz

(b) 30 m, f=4.19 Hz

(c) 35 m,f=3.52 Hz图7 桥梁一阶正对称竖弯模态Fig.7 First-order positive symmetric vertical bending modes of the bridges

3 不同跨度下耦合系统动力响应分析

3.1 简支梁动力响应时频域分析

35 t+35 t+35 t磁浮列车在不同跨径的简支梁上以速度160 km/h运行时(下同)，简支梁跨中竖向动挠度和加速度的对比曲线，如图8和图9所示。

图8 不同跨径简支梁跨中竖向动挠度对比图Fig.8 Comparison diagram of vertical dynamic deflection of simple supported beams at midspan with different spans

(a) 时域

(b) 频域图9 不同跨径简支梁跨中竖向加速度对比图Fig.9 Comparison diagram of vertical acceleration of simply supported beams at midspan with different spans

从图8可知，当简支梁的跨径从25 m增加到35 m时，桥梁跨中动挠度最大值依次为3.32 mm、3.96 mm和4.60 mm。

从图9(a)可知，当简支梁的跨度逐渐增加，桥梁跨中竖向加速度最大值依次为0.28 m/s2、0.21 m/s2、0.15 m/s2，简支梁的竖向加速度随着桥梁跨径的增加而明显减小；从图9(b)可知，各桥梁竖向加速度最大峰值对应的频率点分别为4.8 Hz、4.2 Hz、3.6 Hz，这与简支梁的一阶竖弯频率相对应。

3.2 磁浮车辆动力响应时频域分析

磁浮列车在不同跨径的简支梁上运行时磁浮车体的竖向动位移和加速度的对比曲线,如图10和图11所示。

图10 不同跨径下车体竖向动位移对比图Fig.10 Comparison diagram of vertical dynamic displacement of different span vehicle body

(a) 时域

(b) 频域图11 不同跨径下车体竖向加速度对比图Fig.11 Comparison diagram of vertical acceleration of simply supported beams with different spans

从图10可知，当悬浮车辆在不同跨径简支梁上运行时，车体竖向动位移的最大值依次为3.28 mm、3.89 mm、4.52 mm，车体竖向动位移随着桥梁跨径的增加而增大。同时可以发现，磁浮车辆的竖向动位移与桥梁的竖向动挠度基本一致。

从图11(a)可知，随着简支梁跨径的增加，车体竖向加速度的最大值依次为0.19 m/s2、0.17 m/s2、0.16 m/s2，车体竖向加速度逐渐减小；从图11(b)可知，车体竖向加速度的优势频段均集中在0～15 Hz，为低频振动，峰值频率均为1.0 Hz。在不同跨径下，车体加速度频谱图的分布规律基本一致，仅幅值大小有所差异，这表明车体加速度频谱分布受简支梁跨径的影响较小。

3.3 悬浮架动力响应时频域分析

磁浮列车在不同跨径的简支梁上运行时悬浮架的竖向动位移和加速度的对比曲线,如图12和图13所示。

图12 不同跨径下悬浮架竖向动位移对比图Fig.12 Comparison diagram of vertical dynamic displacement of suspension frame with different spans

(a) 时域

(b) 频域图13 不同跨径下悬浮架竖向加速度对比图Fig.13 Comparison diagram of vertical acceleration of suspension frame with different spans

从图12可知，当简支梁跨径从25 m增加到35 m时，悬浮架竖向动位移的最大值依次为4.01 mm、4.50 mm、4.86 mm，悬浮架的竖向动位移逐渐增加。

从图13(a)可知，悬浮车辆在不同跨径简支梁上运行时，悬浮架加速度的最大值依次为2.12 m/s2、1.94 m/s2、1.79 m/s2，悬浮架竖向加速度随着桥梁跨径增加而逐渐减小。从图13(b)可知，频谱图的第一个峰值频率为1.0 Hz，这与悬浮车体的二系悬挂竖向固有频率和车体竖向加速度的第一个峰值频率相对应，最大峰值频率为11.2 Hz。总体来说，悬浮架竖向加速度明显大于车体竖向加速度；车体竖向加速度频谱分布比较集中，悬浮架竖向加速度的频谱分布较广泛，并含有显著的高频振动成分。这是由于二系悬挂的刚度较小，具有较好的隔振效果，根据隔振原理[19]，其将由悬浮架传递过来的高频振动隔掉，从而使车体表现为低频振动。不同跨径简支梁悬浮架加速度频谱图的分布规律基本一致，仅幅值大小有所差异，这表明悬浮架加速度频谱分布受简支梁跨径的影响较小。

3.4 悬浮控制系统动力响应时频域分析

为更清晰地探讨磁浮列车-桥梁系统动力相互作用的机理，悬浮间隙及电磁悬浮力在不同简支梁跨径下的曲线图,如图14和图15所示。

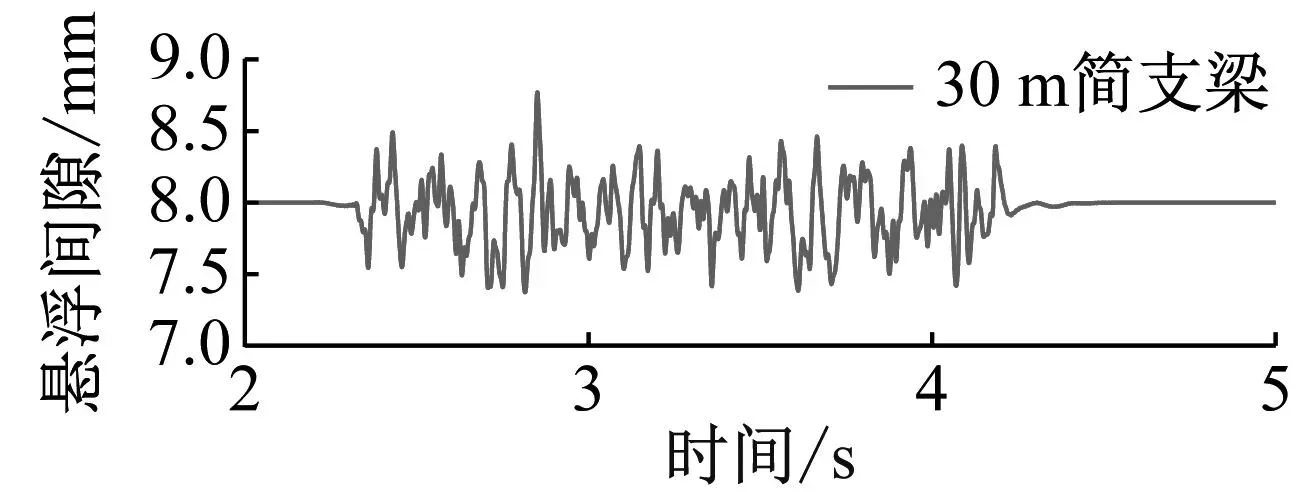
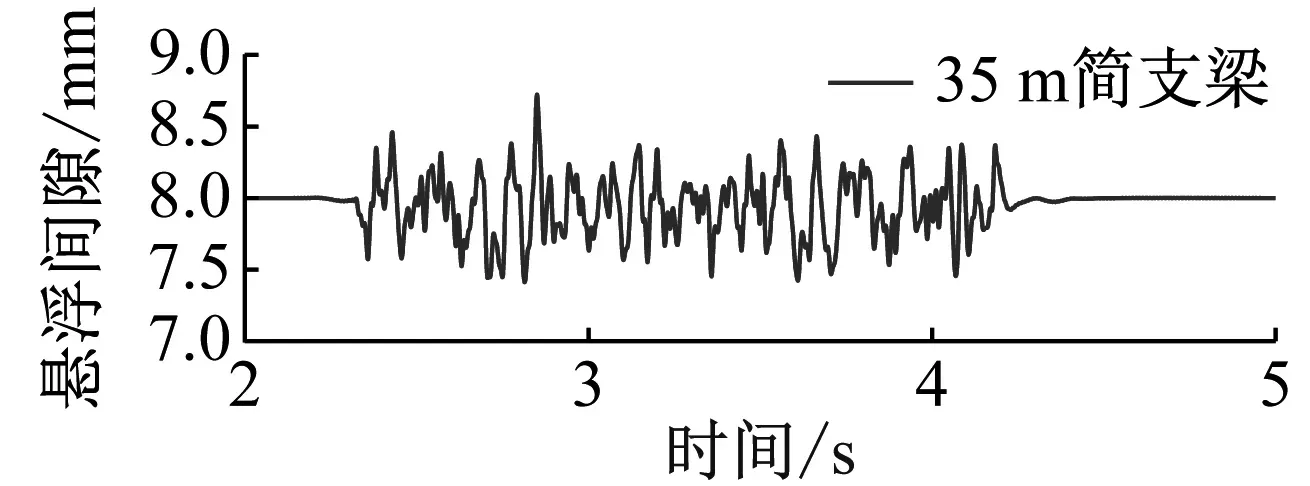
(a) 时域

(b) 频域图14 不同跨径悬浮间隙对比图Fig.14 Comparison diagram of suspension gap of different spans

(a) 时域

(b) 频域图15 不同跨径悬浮力对比图Fig.15 Comparison diagram of suspension force of different spans

从图14可知，悬浮系统通过调节电磁悬浮力，使悬浮电磁铁持续稳定在额定悬浮间隙附近(8 mm)波动，且波动范围都是较小的。这说明了磁浮列车平稳运行时，电磁悬浮系统能够很好地实施主动控制调节，因此磁浮车体的动位移与桥梁的动挠度数值基本相等。在稳定悬浮的基础上，随着简支梁跨径的增加，悬浮间隙和电磁悬浮力的波动范围逐渐减小。

从图15可知，悬浮间隙和悬浮力波动值频段分布集中在0～40 Hz，在11.2 Hz处出现共同的峰值，这与悬浮架加速度频谱图的峰值频率相对应。不同跨径简支梁的悬浮间隙和悬浮力波动值的频谱分布规律几乎相同，仅幅值大小有所差异，这表明简支梁的不同跨径对悬浮间隙和悬浮力波动的频率分布规律影响甚微。

4 跨径对耦合系统动力响应影响机理探讨

4.1 跨径变化对桥梁动力响应影响机理

桥梁的竖向刚度可以根据桥梁挠跨比来确定，挠跨比越小，桥梁竖向刚度越大[20]，25 m,30 m和35 m简支梁挠跨比分别为L/7 530、L/7 576、L/7 609，其竖向刚度逐渐增大。文献[21]指出增加桥梁的质量和刚度，均能降低桥梁的竖向加速度。当简支梁跨径增大，其梁高越高，桥梁的质量增大，同时桥梁的竖向刚度增加，因此桥梁竖向加速度逐渐减小。

磁浮列车在简支梁上运行时，简支梁会产生周期性振动。周期不平顺荷载激励，其激励频率计算公式为

(9)

式中:v为列车运行速度(m/s);λ为周期性不平顺波长(m);f为由周期性不平顺引起的激励频率(Hz)。根据式(9)可得，随着简支梁跨径的增加，由桥梁变形产生的不平顺波长也增长，其引起的激励频率将减小。简支梁跨径变化通过改变由桥梁变形引起的不平顺波长，从而改变桥梁自身的频谱分布特性。

4.2 跨径变化对车辆动力响应影响机理

文献[22]指出悬浮控制系统对长波激励有更好的调节作用。当简支梁跨径增大，由桥梁挠度所形成的不平顺波长越长，悬浮控制系统能更好地调节悬浮间隙性能,车辆对不同跨径简支梁作用如图16所示。因此，悬浮间隙和悬浮力波动值随着简支梁的跨径增加而减小。

图16 车辆对不同跨径简支梁作用示意图Fig.16 Schematic diagram of vehicle action on simply supported beams with different spans

由上面分析可知，悬浮力波动值随着简支梁跨径的增大而减小，而悬浮架质量不变，悬浮架加速度越小。随着简支梁跨径增大，悬浮架振动能量越小，经过二系悬挂隔振后传递给车体的振动能量越小。所以随着简支梁跨径的增大，悬浮架和车体的振动加速度均减小。

5 结 论

本文的主要结论如下：

(1) 简支梁竖向动挠度随着桥梁跨径的增加而增大，竖向加速度随着跨径的增加而减小。25 m、30 m、35 m跨径简支梁的峰值频率分别为4.83 Hz、4.19 Hz、3.52 Hz，这与简支梁的一阶竖弯频率相对应。简支梁跨径变化会改变因桥梁变形引起的不平顺波长，从而改变桥梁自身的频谱分布特性。

(2) 针对不同跨径的桥梁，悬浮控制系统均能实现良好的控制，随着简支梁跨径的增加，悬浮间隙和电磁悬浮力的波动范围逐渐减小，车体和悬浮架的竖向动位移和加速度逐渐减小。悬浮架竖向加速度的优势频段集中在0～30 Hz，同时还包括显著的高频振动(50～80 Hz)，车体竖向加速度的优势频段集中在0～15 Hz，整体表现为低频振动，且幅值较小。

(3) 不同跨径的桥梁通过其模态波长来影响悬浮控制系统和车辆的动力响应，跨径越大，模态波长越大，长波激励的效应就越明显，从而影响作用于桥梁上的悬浮力，进而影响桥梁结构的动力响应。

(4) 磁浮列车在25 m、30 m、35 m简支梁上运行时，桥梁最大动挠度均小于竖向挠度比限制L/4 600，桥梁竖向加速度幅值均较小；车体和悬浮架竖向加速度幅值均较小，磁浮列车运行平稳性均满足要求。因此，磁浮线路可根据当地环境，灵活地选择简支梁的跨径，最大程度节约工程造价。