混凝土腐蚀减薄对钢筋混凝土管节承载性能影响
刘 赫, 刘俊博, 朱子豪, 赵雅宏,王志钢, 矫立新, 栾靖尧, 张 鹏
(1. 国网吉林省电力有限公司电力科学研究院, 吉林 长春 130012; 2. 中国地质大学(武汉) 工程学院,湖北 武汉 430074; 3. 国网吉林省电力有限公司辽源供电公司, 吉林 辽源 136200)
钢筋混凝土管节被广泛用于各类地下通道结构中,包括给排水管道、电力隧道、综合管廊等。在地下环境中,管节内侧混凝土保护层在腐蚀性介质的长期作用下受到腐蚀作用,产生常见的蜂窝麻面、露筋等缺陷,导致管节壁厚减薄以及承载能力降低。混凝土腐蚀过程复杂、种类繁多,分类标准有很多种,按侵蚀介质种类分为两大类。第一类为无机物侵蚀:包括酸、盐、强碱与混凝土的组成成分发生化学反应,生成无凝胶作用或膨胀性物质,改变混凝土结构成分,因而导致混凝土腐蚀;第二类为有机物与微生物侵蚀:在适当的环境中,微生物分解消化有机物,释放有机酸、二氧化碳、硫化氢等腐蚀性介质,使混凝土劣化。文献[1]中给出了常见的化学和生物因素对混凝土的腐蚀作用机理,如表1[1]所示。因此,对于已经发生壁厚减薄的钢筋混凝土管节,采用合适的理论模型评价其剩余承载能力是十分有必要的,这也是本文主要研究的问题。
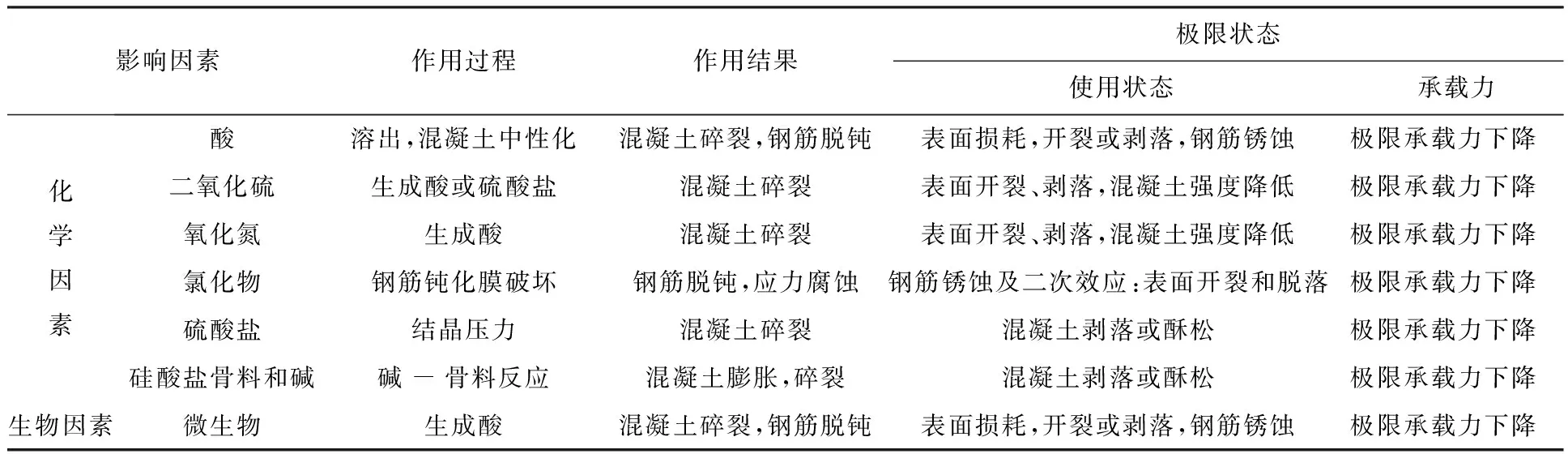
表1 常见的化学和生物因素对混凝土的腐蚀作用机理
目前对管道腐蚀减薄的研究主要集中于钢质油气管道,在该领域研究者们关注更多的是钢管受腐蚀之后的剩余内压承受能力而非剩余的荷载承载能力,提出了断裂力学半经验公式法[1]、D - M失效图判定法[2]、弹塑性力学方法[3]等,这些方法主要以薄壁均质圆筒模型为假设,虽然广泛地应用于石油管道领域,但在钢筋混凝土管道这样的非均质厚壁圆筒的情况下无法应用。
对于钢筋混凝土管腐蚀后的剩余承载力,主要有以下两个研究角度:
一个是对混凝土中氯离子和硫酸根离子等的扩散规律及扩散浓度对混凝土强度的影响,以及钢筋锈蚀后的抗拉及抗压性能进行研究[4~6],这些研究能够较为精确地反映腐蚀液体与钢筋混凝土材料的作用规律,但是整体尺度较小,且需要测量的参数较为繁杂,难以应用于钢筋混凝土管节结构的现场检测与评价。另一方面,对构件受到腐蚀的研究更多的是单独考虑混凝土或者钢筋构件的影响,考虑钢筋混凝土复合构件受腐蚀影响的论文都相对较少[7]。
另一个研究角度则是直接考虑宏观的钢筋混凝土结构受到腐蚀后的影响,在这一部分绝大多数的研究集中在钢筋混凝土梁结构[8]或者柱结构[9]上,对管道结构腐蚀的研究屈指可数,只有Li Bin[10]对腐蚀混凝土管的承载性能进行了研究,然而该文献研究的对象是素混凝土管,且腐蚀区域设置在管顶的一小片区域。
综上所述,鲜有对钢筋混凝土管节发生整体腐蚀减薄后承载能力的研究。为此,本文基于管道的塑性铰破坏模式提出了钢筋混凝土管节剩余承载能力计算模型,在此基础上给出了腐蚀减薄钢筋混凝土管节的承载能力模型,并结合三点法外荷载(Three-edge Bearing,TEB)试验验证了所得模型的准确性,对各类地下通道结构(电缆通道、综合管廊、排水管道等)受到腐蚀之后的承载能力提出了一种简单易行的评价方法,对实际工程有较好的指导意义和应用价值。
1 钢筋混凝土管节TEB承载力模型
1.1 无损管节承载力模型
根据GB/T 16752—2017《混凝土和钢筋混凝土排水管试验方法》[11],圆形截面的钢筋混凝土管采用三点法外荷载(TEB)试验来测定其承载能力,TEB试验中结构所受到的荷载形式及其简化如图1所示。
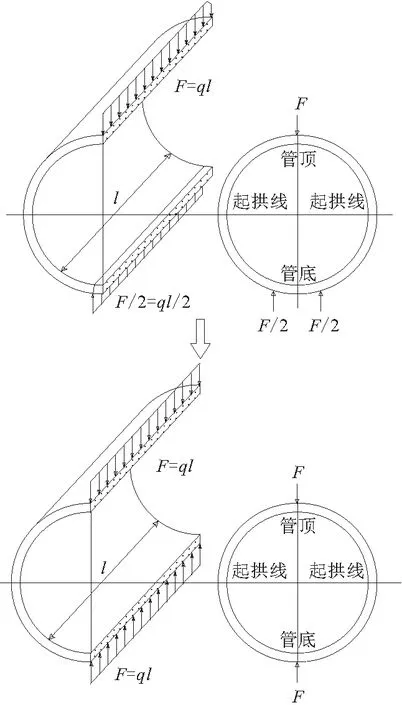
图1 管节所受荷载简化模型
简化后的荷载模型为轴对称的基本结构,圆形管节的破坏模式为塑性铰破坏,即在管节顶部(crown)、底部(invert)和两侧起拱线(springline)处开裂成四片,相连处假设其形成四个塑性铰,四片刚性管片以塑性铰为铰支点继续发生转动变形,这种状态下的钢筋混凝土管可以看做柔性管道处理,如图2所示。
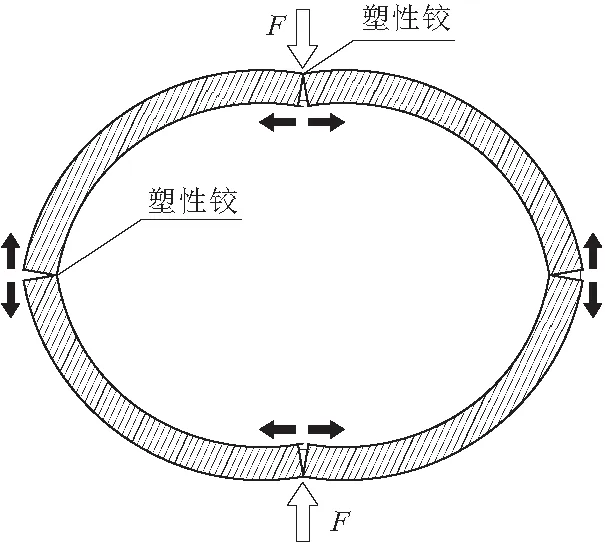
图2 管节在竖向荷载作用下发生塑性铰破坏
Ian等[12]指出,当管节发生塑性破坏时,其极限承载力F为:
(1)
在文献[12]中,Ian进一步地将公式(1)简化为
(2)
式中:F为管节极限承载力(N);R为管节平均半径(mm);Mpcrown/pinvert/pspringline为管道破坏时管顶、管底及两侧产生的极限弯矩(N·mm)。
由于文献[12]的研究对象是钢波纹管,其在管顶、管底及两侧截面形式相同且材料属性均匀,因此式(2)的简化是可行的。然而对于本文所研究的钢筋混凝土管道而言,其内外侧箍筋的截面积不同,且对于同一根箍筋,以外层钢筋笼为例,其在管顶和管侧受力形式也不同,因此管顶(底)和两侧的截面形式是不一样的,为此,本文提出改进公式如下:
(3)
式中:Mpcrown=Mpinvert=Mv;Mpspringline=Mh;Mv为竖直方向(管顶和管底)截面发生塑性破坏的极限弯矩(N·mm);Mh为水平方向(起拱线)截面发生塑性破坏的极限弯矩(N·mm)。
对于Ⅱ级管而言,管内径≥1000 mm采用双层配筋[13],其截面形式为正截面受弯的双筋矩形截面受弯构件,管顶及起拱线处截面分别如图3b,3c所示, 当管节发生塑性铰破坏时,假设在极限条件下除了铰支点其余混凝土截面均被拉裂,内外箍筋在这种情况下均受拉应力作用,仅有铰支点受压。
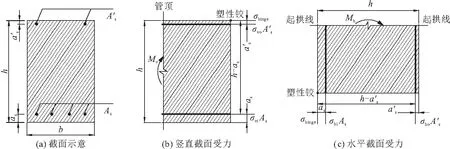
图3 管节截面
此时对铰支点取矩可以分别求得管顶和起拱线截面处弯矩值Mv和Mh:
Mv=σvoA′sa′s+σviAs(h-as)
(4)
Mh=σhiAsas+σhoA′s(h-a′s)
(5)
式中:σvo,σvi分别为管顶截面外、内侧箍筋的拉应力(MPa);σho,σhi分别为起拱线截面外、内侧箍筋的拉应力(MPa);As,A′s分别为计算截面内、外侧箍筋的截面积(mm2);h,b分别为计算截面高度、宽度(mm);as,a′s分别为管节内/外保护层厚度(mm)。
应用于电缆通道等大断面地下通道结构的钢筋混凝土管节,往往采用流幅较小的高强钢筋,此时可以采用双斜线模型来描述钢筋的弹塑性[14],如图4所示。
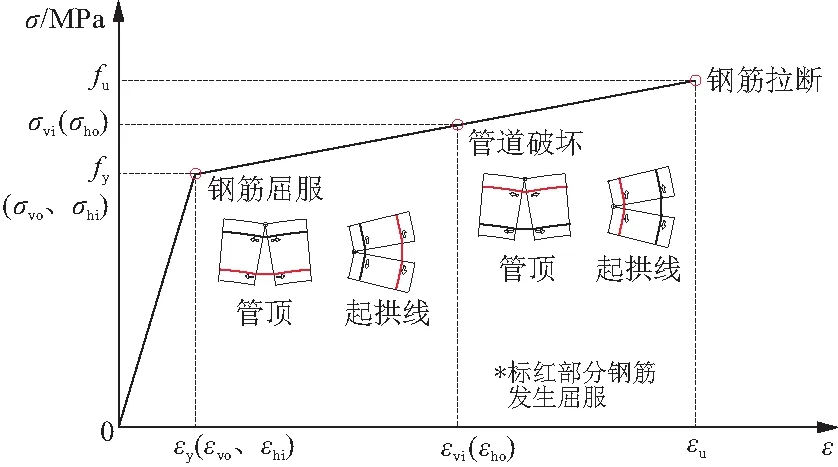
图4 钢筋应力 - 应变关系
以管顶截面为例,当作用于管顶荷载逐渐增大,内侧受拉钢筋首先达到屈服阶段,但是管节此时还未发生整体破坏。随着裂缝张开,管顶外侧钢筋也发生屈服,此时管节发生整体破坏,破坏后的管道碎裂成四个管片,但彼此之间一般仍有钢筋相连,即荷载达到管道最大承载能力时,钢筋中的拉应力仍未达到其抗拉强度,对于管节起拱线处截面其破坏规律亦类似。基于此,将管顶外侧钢筋和起拱线内侧钢筋屈服作为管节截面破坏判据,可以分别推导得到管顶和起拱线处内外层钢筋的应力应变关系:
(6)
(7)
且从图4可知:
(8)
σvo=σhi=fy
(9)
式中:εvi,εvo分别为竖向截面中内、外侧钢筋应变;εhi,εho分别为水平截面中内、外侧钢筋应变;fu,fy分别为钢筋的抗拉强度、屈服强度(MPa);εy,εu分别为钢筋屈服和破坏时应变(伸长率);E为钢筋弹性模量(MPa)。
管节完全开裂时,假设在有限的裂缝开度下管道内外层钢筋是协调变形的,于是有如图5所示模型,根据几何关系可以得到管顶和起拱线处内外侧管节协调变形公式:
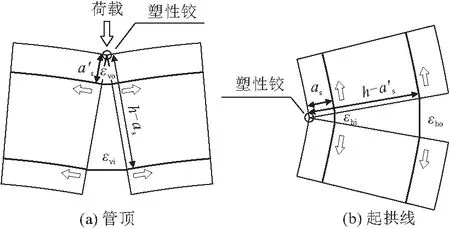
图5 内外层钢筋协调变形模型
(10)
(11)
联立式(6)~(11)可以求出管道破坏时管顶内侧和起拱线外侧钢筋中的拉应力值σvi和σho:
(12)
(13)
将式(12),(13)代入式(3)~(5),即可得到无损钢筋混凝土管节在TEB条件下的最大承载能力:
(14)
其中:
(15)
1.2 混凝土腐蚀减薄管节剩余承载力模型
上一小节推导了无损管节的TEB承载能力模型,本节将以此为基础推导混凝土腐蚀减薄钢筋混凝土管节的剩余承载力。结合前人研究[1,15],将表1中的各类混凝土腐蚀机理进行整理和简化分析,腐蚀作用对钢筋混凝土结构的影响主要从以下3个方面体现:(1)管壁的腐蚀减薄;(2)钢筋锈蚀;(3)混凝土与钢筋粘结强度降低。由于本文主要讨论混凝土腐蚀引起的壁厚减薄作用对管节承载性能的宏观影响,因此不考虑钢筋锈蚀引起的强度折减和粘结性能降低。在此基础上,可以做出如下假定:
(1)本文主要研究内容是钢筋混凝土管壁的腐蚀减薄,也即管道壁厚的折减和平均半径的增大,根据不同的混凝土腐蚀深度需要分情况考虑。当混凝土腐蚀深度小于保护层厚度时,由于保护层抗拉强度低,主要起防腐保护作用,因此即使发生减薄对结构承载性能的影响也较小,而当混凝土腐蚀深度大于保护层厚度,此时损失的是截面的有效高度,因此承载能力会开始大幅降低;
(2)钢筋锈蚀率会使钢筋的有效截面积减小,屈服强度和抗拉强度降低,引入钢筋锈蚀折减系数kr来表示该变化,kr的取值与钢筋有效截面积和钢筋抗拉强度均有关,二者均可通过室内试验测得,由于本文仅讨论混凝土腐蚀减薄对钢筋混凝土管节剩余承载力的影响,因此将kr设为1;
(3)文献[14]给出了钢筋 - 混凝土界面粘结力的组成形式,其中光圆钢筋的粘结力主要来自于胶结力和摩阻力,螺纹钢筋的粘结力主要来自于机械咬合作用。从定义上来看,不论是胶结力、摩阻力还是机械咬合力,均是与钢筋 - 混凝土界面的接触面积成正相关的,因此暴露在外的钢筋面积越多,钢筋 - 混凝土接触面积越小,界面的粘结力也越低。在此基础上,本文给出钢筋 - 混凝土界面粘结强度折减系数kb,该系数与钢筋 - 混凝土接触面积比、钢筋有效截面积、腐蚀后的钢筋和混凝土强度均有关。本文也仅考虑了由于管节壁厚减薄导致的钢筋 - 混凝土界面粘结折减,不包括钢筋的锈蚀、锈胀作用等造成的界面粘结性能变化。下文会给出kb的取值方法,并结合试验进行评价。
基于上述假定,结合1.1节所推导的无损管节剩余承载能力公式,可以推导得到腐蚀减薄管节的剩余承载能力。其中对于管顶位置截面,虽然其内侧保护层厚度减小,但是内、外层钢筋受拉作用点到塑性铰的距离没有发生变化,因此管顶截面能承受的最大弯矩为:
M′v=kr[σvokbA′sa′s+σviAs(h-as)]
(16)
式中:M′v为腐蚀钢筋混凝土管节竖直截面承受的最大弯矩(N·mm);d为混凝土腐蚀深度(mm)。
当管节内侧发生腐蚀后,起拱线处截面的受力情况与管顶截面相比则发生较大变化,内侧保护层的减薄会使得模型中塑性铰的位置外移,受压点向内侧钢筋逼近,混凝土腐蚀深度小于内侧保护层厚度时,内、外层钢筋的协调变形关系变为:
(17)
于是有:
σ′hi=σhi=fy
(18)
(19)
式中:ε′ho为腐蚀减薄管节起拱线处外侧钢筋应变;ε′hi为腐蚀减薄管节起拱线处内侧钢筋应变;σ′hi为腐蚀减薄管节起拱线处内侧钢筋应力(MPa);σ′ho为腐蚀减薄管节起拱线处外侧钢筋应力(MPa)。
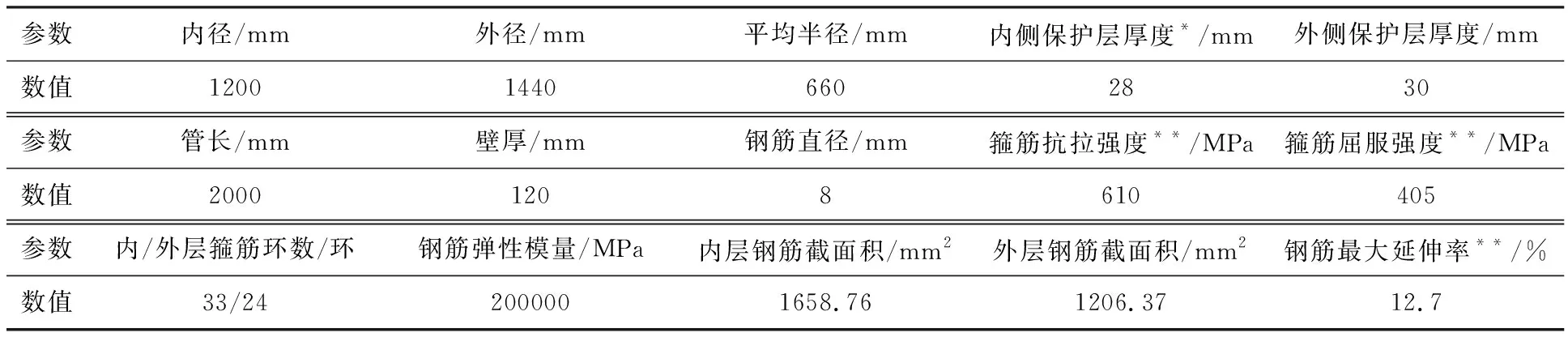
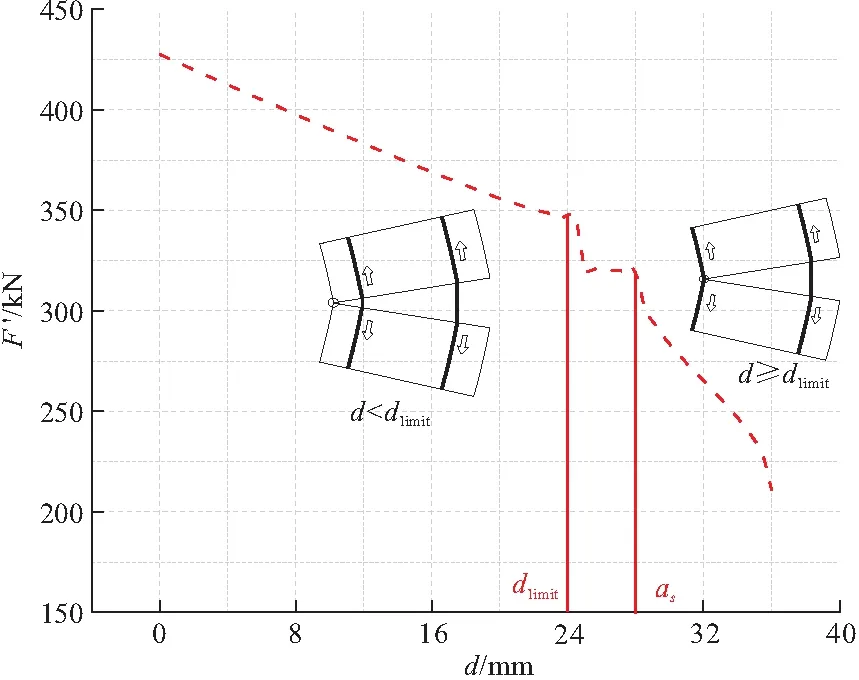
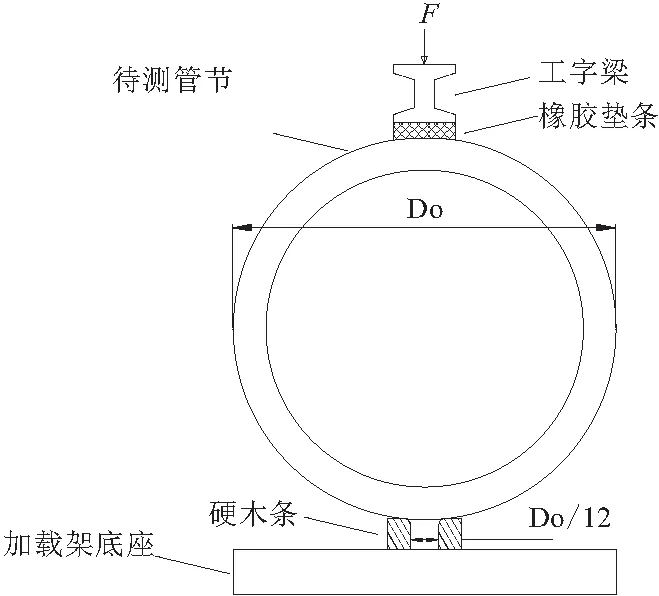
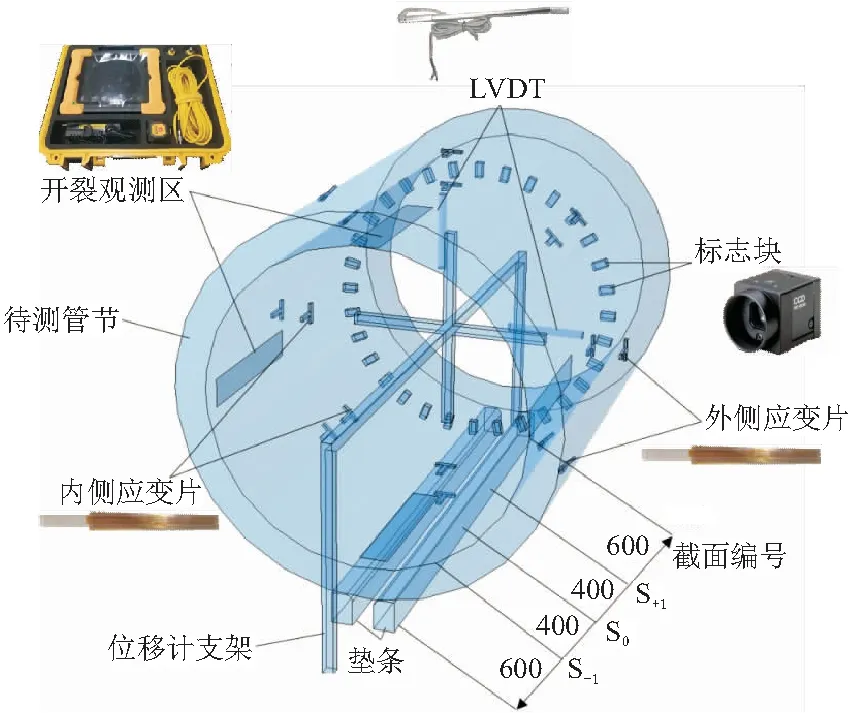
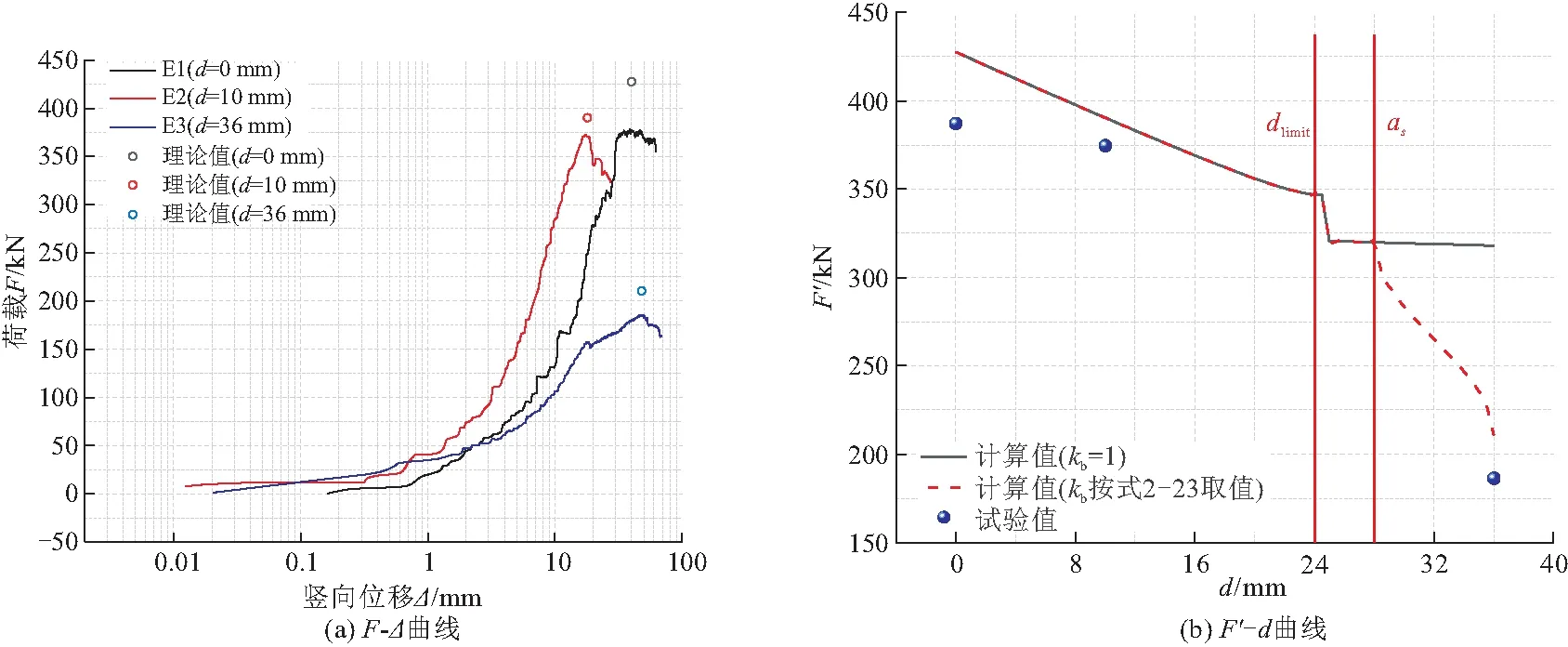
不难看出式(19)的应用是有限制的,主要体现在两个方面:(1)σ′ho (20) 因此,采用塑性铰模型进行计算时,当混凝土腐蚀深度d 图6 起拱线处腐蚀减薄后截面受力情况 于是可以得到: (21) 式中:M′h为腐蚀钢筋混凝土管节水平截面承受的最大弯矩(N·mm)。 联立式(3),(16),(21),即可求得腐蚀缺陷混凝土管节在TEB条件下的剩余承载能力公式: (22) 式中:F′为腐蚀钢筋混凝土管节剩余承载力。 试验所用的钢筋混凝土管节的各项参数如表2所示。 表2 试验用钢筋混凝土管节性能参数 将上述各项参数代入式(14), 求得该管节在无损条件下的TEB承载力约为427.55 kN,内外层钢筋协调受拉变形的极限混凝土腐蚀深度dlimit=24.3 mm。 如1.2节所述,本文仅讨论腐蚀减薄深度对钢筋混凝土管节剩余承载力的影响,因此将钢筋的材料强度折减系数kr设为1,此时kb仅受到钢筋暴露面积比的影响,按照式(23)进行取值,该取值是依据内保护层腐蚀后钢筋未暴露的面积比(也即钢筋 - 混凝土接触部分面积比)进行简化计算,后文会采用试验方法讨论该取值方法的适用性。 (23) 当腐蚀至内层箍筋完全暴露时,混凝土腐蚀深度d=36 mm,在此范围内采用公式(22)计算腐蚀管节的TEB剩余承载力,混凝土腐蚀深度对剩余承载力的影响如图7所示。 图7 理论计算的F′-d曲线 从图7中可以看到,随着混凝土腐蚀深度的增加,管节的剩余承载力呈阶段性线性下降趋势,当混凝土腐蚀深度达到dlimit时,管节的剩余承载力降低了18.9%;混凝土腐蚀深度大于dlimit之后,剩余的混凝土保护层无法承担铰支点处的压应力,内层钢筋作为新的塑性铰支点受压,此时只有外层钢筋受拉,由于采用分段函数进行计算,剩余承载力呈现断崖式下降,混凝土腐蚀深度达到28 mm时,管节剩余承载力为无损管节的74.82%。可以看到混凝土腐蚀深度达到dlimit之后,随着混凝土腐蚀深度增加,管节剩余承载力的下降反而变得不明显,这是由于当以内层钢筋作为塑性铰支座进行计算之后,即使混凝土腐蚀深度继续加深,外层钢筋中拉力对铰支座取矩的距离始终保持不变,所以M′h也不变。当混凝土腐蚀深度大于as后,由于钢筋笼开始暴露,kb按照钢筋 - 混凝土接触面积比进行折减,管节的剩余承载力再次发生较大折减,此时混凝土和钢筋之间的脱空导致二者之间的协调变形失效。 在理论研究的基础上,本节采用TEB试验对腐蚀减薄管节的剩余承载力进行研究。根据GB/T 16752—2017《混凝土和钢筋混凝土排水管试验方法》[11],TEB试验的试验装置如图8所示,主要包括加载架、下支承梁、上支承梁以及垫条。本次试验采用1000 kN电液伺服静力加载系统对待测管节进行竖向加载。上支承梁为一根矩形钢梁,宽0.3 m,长度与待测管节长度相等(2 m),钢梁上部与加载机头相连,钢梁与管节之间铺设橡胶垫条以使荷载均匀分布到管节外表面。下支承梁由两根0.2 m×0.2 m×2 m的硬木组合而成,同样与待测管节等长,且两根硬木之间的距离为待测管节外径的1/12(120 mm)。 图8 试验装置示意 TEB试验共设置3组,包括1组无损管节试验和2组腐蚀减薄试验,如表3所示。 表3 模型试验各组别及参数 mm TEB试验过程主要包括以下步骤: (1)管节预处理。E1无须经过预处理,E2和E3对内保护层进行减薄处理,采用风镐进行人工凿毛处理的方式进行模拟,如图9所示。凿毛后采用激光测距仪测量管内10个不同方向及位置的内径并取平均值,得到E2中的凿毛深度(混凝土腐蚀深度)约为10 mm,E3中凿毛深度(混凝土腐蚀深度)约为36 mm,从图9d中可以看到,开凿后管节内圈箍筋几乎完全露出,部分位置内圈钢筋笼已经与混凝土基体脱空。 图9 管节内部凿毛减薄处理 (2)传感器布设。TEB试验管节内部布置及各传感器实物照片如图10所示,管节沿纵向划分3个断面,分别标记为S-1,S0和S+1。其中S0为管节中间位置截面,S-1和S+1分别往两侧偏移400 mm。在3个断面依次采用裂缝观测仪、LVDT压电式位移计及应变片、CCD高速相机进行测量。其中,裂缝观测采用HC-U81混凝土超声波检测仪对分级加载过程不同阶段的管顶、管底及侧面裂纹的宽度及深度进行观测测量;竖直及水平方向变形量采用两只LVDT20-100 mm差动变压器式位移传感器进行实时监测;采用82 mm×11 mm电阻式应变片在管节内外两侧的管顶、管底、两侧起拱线及45°位置进行应变测量;在管节内部S+1截面沿环向均匀布设32个标志块,采用不同的几何图案加以区分,在正对标志块一侧管节外架设CCD(Charge Coupled Device,电荷耦合元件)相机对管节加载全过程进行快速拍照(1 fps)。所有参数均通过NI采集通道进行实时采集和上传。 图10 试验管节内部布置/mm (3)分级加载。试验过程中,采用控制位移的方法对管节分级进行加载,在0~150 kN时加载速率为3 mm/min,随后改为以1 mm/min的速率加载直到管节破坏。 E1~E3组试验中测得的管道F-Δ曲线如图11a所示,并将理论计算得到的管节承载能力标于图中进行对比,其中无损管节(d=0 mm)的承载能力为389.17 kN,比理论值(427.55 kN)低8.98%,混凝土腐蚀深度d≤dlimit(d=10 mm)时,管节剩余承载能力为374.55 kN,比理论值(390.36 kN)低4.05%,混凝土腐蚀深度d>dlimit(d=36 mm)时,管节剩余承载能力为186.41 kN,比理论值(318.00 kN)低41.38%。可以看到,当d≤dlimit时,试验值和理论值的误差在10%以内,而当d>dlimit之后,可以看到管节的剩余承载能力有了大幅的下降,说明钢筋与混凝土是否协调变形会在很大程度上影响管节的承载能力。 图11b中显示了剩余承载力计算值和试验值的对比情况。其中,对于计算值图中给出了kb分别按1和式(23)进行取值的计算结果,同样以dlimit作为分界线,可以看出在d 图11 实测的F-Δ曲线对比和剩余承载力理论 - 试验值对比 本文得到的主要结论包括: (1)结合管道力学中的塑性铰模型和双筋矩形受弯截面分析,推导了双层配筋钢筋混凝土管在TEB试验中的最大承载力计算公式,并在此基础上推导了钢筋混凝土管腐蚀减薄后,其剩余承载力与混凝土腐蚀深度之间的关系; (2)对钢筋混凝土管节进行室内TEB试验,分别对无损、保护层未完全腐蚀和保护层完全腐蚀的管节进行试验,测得其剩余承载力大小并与理论值相比较。结果表明,当混凝土腐蚀深度小于钢筋协同受拉变形极限混凝土腐蚀深度(d≤dlimit)时,试验结果与模拟值和理论值均较为接近,而当混凝土腐蚀深度达到保护层厚度后,试验测得的管节剩余承载力要明显低于理论值,这是由于保护层完全腐蚀后,钢筋与混凝土界面开始发生剥离,二者之间的粘结系数kb开始下降,采用钢筋 - 混凝土界面接触面积比来表征系数kb的值并对公式进行修正,修正后的结果可以较好的吻合实验情况。 (3)本文所得到的腐蚀减薄缺陷钢筋混凝土管节剩余承载力计算模型能够应用于各类地下通道结构(电缆通道、综合管廊、排水管道等)的检测评估中,结合检测得到的各项参数可以算出缺陷通道结构的剩余承载力,将其与结构目前所承受的外荷载进行对比,能够较好地评价缺陷地下通道结构的服役现状及安全性,并依据评价结果对其进行进一步的修复或更新处理,有较大的工程应用价值。 (4)本文研究了混凝土腐蚀减薄对钢筋混凝土管节承载能力的影响,并进行了三点法外荷载试验。由于试验条件限制,采用人工凿毛的方法进行管节内壁处理,以此模拟管节的减薄,这样处理同样忽略了钢筋锈蚀对承载能力降低的影响,因此得到的计算模型中钢筋的强度折减系数kr取为1。这样虽能更好地反映管节混凝土保护层减薄单一因素对剩余承载力的影响,但是在实际情况中,混凝土的腐蚀和钢筋的锈蚀往往是同时出现的,因此本文计算模型仍有一定局限性,需要结合钢筋锈蚀特征,进一步讨论混凝土保护层腐蚀和钢筋锈蚀耦合作用对结果承载能力的影响,这也可以为后续研究提供思路。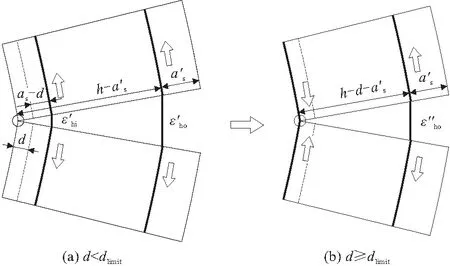
1.3 实例计算
2 腐蚀减薄管节TEB试验
2.1 试验目的与方法
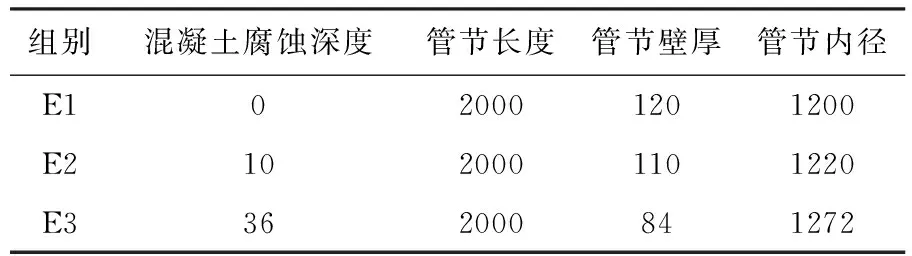
2.2 试验过程

2.3 试验结果及分析
3 结论与展望

