基于GM-ARIMA 模型对贵州省能源需求的预测

张海鹏

（贵州大学 管理学院，贵州 贵阳 550025）

一、引言

改革开放以来，我国经济进入了快速发展阶段，以煤炭、石油为主的化石能源是推动经济发展的主要动力之一。高速的经济增长依赖于大量的能源消费，但能源消费在推动经济发展的同时对环境造成破坏，产生大量的碳排放。因此为了有效控制碳排放，需要政府制定合理的能源管理措施。各种电源的装机容量规划、能源传输线路规划等国家能源战略制定都需要以科学、合理的能源需求预测结果作为参考[1]。所以有必要对未来能源需求进行准确的预测。近年来，在温室效应与生态保护的交叉影响下，世界各地的电力企业都在努力构建一个兼顾碳减排、提高效率和节能减排的环境友好型发展框架[1]。IEA 国际能源署的“能源技术展望”研究报告指出，减少二氧化碳排放的最佳策略包括以下措施：提高最终用户的能源效率（38%），实施碳捕获技术（19%），发展可再生能源（17%），建立最终用户替代品（15%），发展核能发电（6%）和提高发电效率（5%）。后四个措施的针对的都是能源供给侧，这表明减少二氧化碳排放的主要来源是能源供给侧，占比43%[2]。优化长期发电结构、合理配置供给侧能源，是实现二氧化碳减排目标的重要要求，而准确的预测能源需求又是优化长期发电结构、合理配置供电侧能源的前提。

对能源需求的预测方法上，国内外的学者做了大量的研究。能源需求预测涉及的基本的预测方法主要可以分为投入产出法、弹性系数法、随机时间序列法、灰色预测法和神经网络法[3]。Qiao Mei 等（2006）[4]将中国分为八个经济区域，并建立了能源需求的多区域投入产出模型，结果表明各区域能源使用效率的提高可以促进区域内的能源节约。该方法虽然可以预测任意时期能源需求，但是预测精确度不高。谢和平等（2019）[5]将中国的经济发展分为3个阶段，基于弹性系数法对中国的2025 年的能源消费总量进行预测。该方法的优点是模型和求解都简单，但是预测的精确度也不高。1976 年，Box 等（2015）[6]在基于ARMA 模型上提出了自回归综合滑动平均模型（ARIMA 模型）。Garg N 等（2015）[7]利用ARIMA 模型对长期的噪声监测数据进行了分析，研究表明：ARIMA 模型可以用于对交通噪声水平的时间序列建模。Aasim 等提出了一种新的基于重复小波变换的RWT-ARIMA 模型预测短期风速，并与ARIMA 模型和WT-ARIMA 模型作了比较，发现RWT-ARIMA 模型的预测精度更好[8]。灰色模型的应用已扩展到许多领域，例如经济，能源，技术，管理等。梁一鸣和雷社平（2019）[9]在分析中部六省的碳排时，采用GM（1，1）对碳排量和碳排放强度进行了预测，预测显示，这六个区域的碳排放量逐年递增。Yang 等（2019）[10]首次提出了理论碳赤字的概念，此外，利用STIRPAT 和GM（1，1）对中国30 个省份之间的碳补偿成本进行了预测，结果表明2017—2026年，我国30 个省份的碳排放和碳吸收总体呈上升趋势。李俊等（2020）[11]提出了分数阶灰色预测模型农业用水量进行了预测，并于传统模型进行相比，该模型具有更好的精确性。曾波等（2020）[12]利用灰色模型对人体的健康指标和趋势进行了分析。随机时间序列法和灰色预测法对于中短期的预测精度都比较高，且灰色预测法只需要少量的样本数据。付斌等（2017）[13]利用改进的基于L-M 算法BP 神经网络法对我国天然气需求量进行了预测。神经网络法的预测精度也高但建模过程中参数调整需要花费太多时间。

对于能源的需求中长期预测上，随机时间序列法和灰色预测法的构建相对简单且预测精度也较高，但少有文献将两个模型结合起来运用在能源消费预测上。且大多数文献集中在对国家的预测上，对于个别区域的研究较少。贵州省是一个煤炭资源丰富的省份，煤炭又是碳排放最主要的化石能源。近年来，贵州省能源消费大体呈现出逐年递增的状态（个别年份除外），为了合理调整能源消费结构以及确保地方绿色式可持续发展，需要对贵州省能源需求进行准确预测以及分析预测结果。所以，本文以贵州省2011—2020 年的能源需求数据为基础，采用灰色GM（1，1）模型和ARIMA 模型的组合预测模型GM-ARIMA 对贵州省未来的能源需求进行预测。与单一的ARIMA 模型和GM（1，1）模型相比，该模型可以提高预测的准确性，为贵州省能源需求的预测提供科学可靠的理论依据，并为相关政策决策提供依据。GM-ARIMA 组合预测模型提供了一种预测未来能源消费的方法，这为未来的能源发展规划，政策制定和技术指导提供了参考价值，为能源结构的调整和能源供需水平的合理调整奠定坚实的基础。通过这些调整，贵州省未来的能源发展将更加绿色和清洁。

二、数据来源与模型原理

（一）数据来源

如表1 所示，本文选择了贵州省2011—2020 年的能源消费作为参考数据（数据来源于最新的《贵州省统计年鉴》），进行预测，并分析了未来五年贵州省的能源需求。

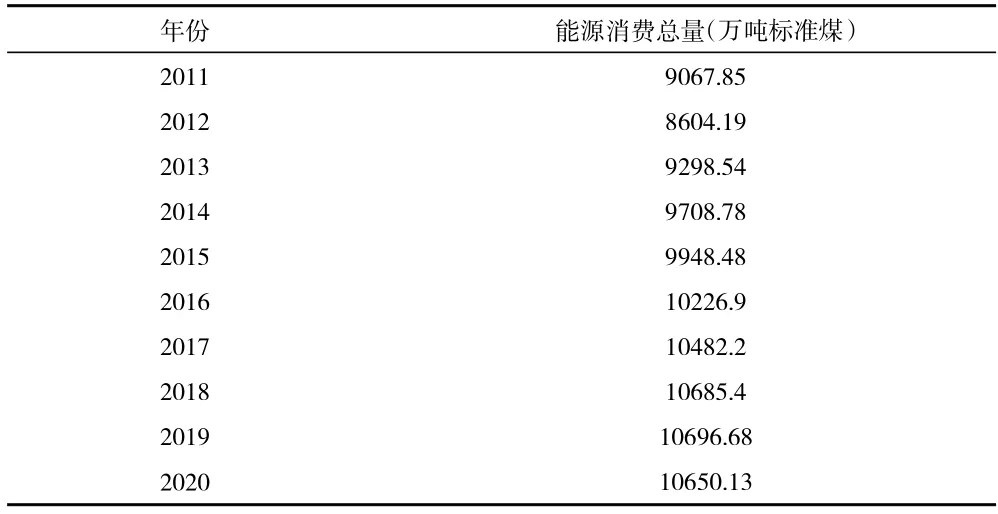
表1 2011—2020 年贵州省能源消费

（二）模型原理

1.ARIMA 模型的原理。差分自回归移动平均模型ARIMA 是自回归模型AR、移动平均模型MA 和差分的结合。ARIMA 模型是利用因变量Yt的滞后值和随机误差项的现值和滞后值进行回归所建的模型，并将该模型用来预测[14]。这个分析已被广泛应用于许多领域的建模和预测，例如医学，环境，金融和工程应用[15]。ARIMA 模型的具体形式可以表示为ARIMA（p，d，q），其中“p”代表自回归项，“d”代表差异项，“q”代表移动平均项。字母“d”代表差分次数：如果序列是稳定的，那么d 为0；如果序列是非稳定的，则需要使其与d 的阶数不同以使其平滑，然后开始建模[16]。时间序列是稳定的充分必要条件是它的所有统计特征都独立于时间，没有任何趋势和周期性。

2.GM（1，1）模型的原理。GM（1，1）模型的特点是用少量的数据（通常为5～10）来预测未来趋势。灰色理论的基本思想是：将已知的时间序列按某种生成方式做数据处理，然后根据特定方法来找到未来发展的规律，灰色理论的核心是建立微分方程。而复杂的数据和系统可以建立微分方程的条件是数据序列中必须存在一定的规律。使用灰色模型的优点在于它不需要大量样本，并且短期预测的效果很好，而能源需求数据具有这些特征，所以灰色模型可用于能源需求的预测。

三、模型构建

（一）ARIMA 模型的构建

经典线性回归模型的一个重要假设是线性回归函数中的随机误差项具有相同的方差。如果不满足这一假设，那么线性回归方程就是异方差的。如果线性回归模型具有异方差性，用传统的最小二乘法对模型进行估计后，估计的参数就不是有效的估计值。此时的显著性检验就是无效的。

（1）为了消除原始时间序列中异方差的可能性，需要用ADF 单位根检验来检验序列的平稳性。如果序列平稳，就不存在单位根；相反，就会有单位根。使用Eviews 软件对原始序列进行一级差分后，ADF测试结果（见表2），表明原始序列是稳定的，即d=1。

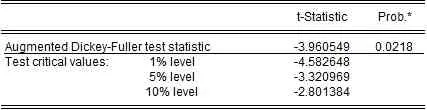
表2 贵州省能源消费平稳性检验（一级差分）

（2）确定了差分阶数d 之后，要确定ARIMA 模型的p 项和q 项。通过对自相关和偏相关函数图的观测，并研究是截尾还是拖尾，就可以确定模型的自回归项和移动平均项。如果自相关（或偏自相关）系数突然收敛到临界水平范围，并且他们的值突然变得非常小，称之为截尾。如果自相关（或偏自相关）系数拖了很长的一条尾巴，并且它的值是缓慢减小的，称其为拖尾。使用SPSS 软件对序列进行拟合后，可以得到自相关系数和偏自相关系数，如图1 所示。

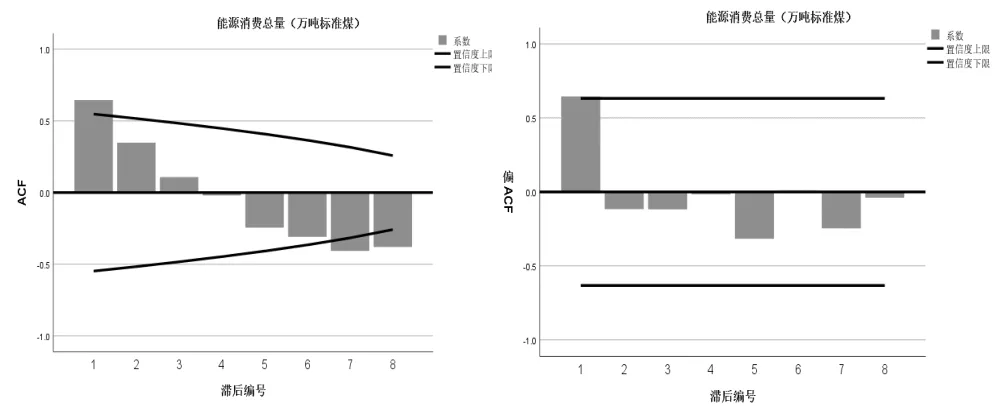
图1 贵州省能源消费自相关函数图（左）与偏自相关函数图（右）

从图1 可以看出自相关函数是遵循指数衰减的，它的值没有突然变得很小。所以，自相关函数处于拖尾状态。而偏自相关函数在1 阶之后为零，具有截尾的特性。所以，应使用AR（1）模型测试时间序列。

（3）确定模型类型后，用SPSS 软件拟合模型。拟合得到AR 参数值为0.936，常数项为8 842.412。然后，如图2 所示，残差的自相关图和偏自相关图显示了平稳的拟合序列，平均相对误差为2.697%。

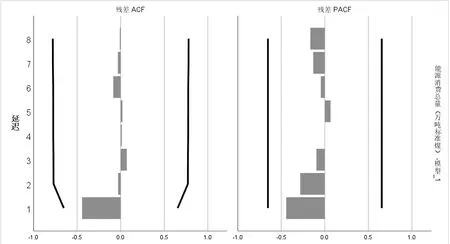
图2 残差的自相关图和偏自相关图

所以，得到的ARIMA 模型公式为：yt=8842.412+0.936yt-1+εt。图3 为得到的模型拟合和预测结果图，可以看出拟合效果良好。

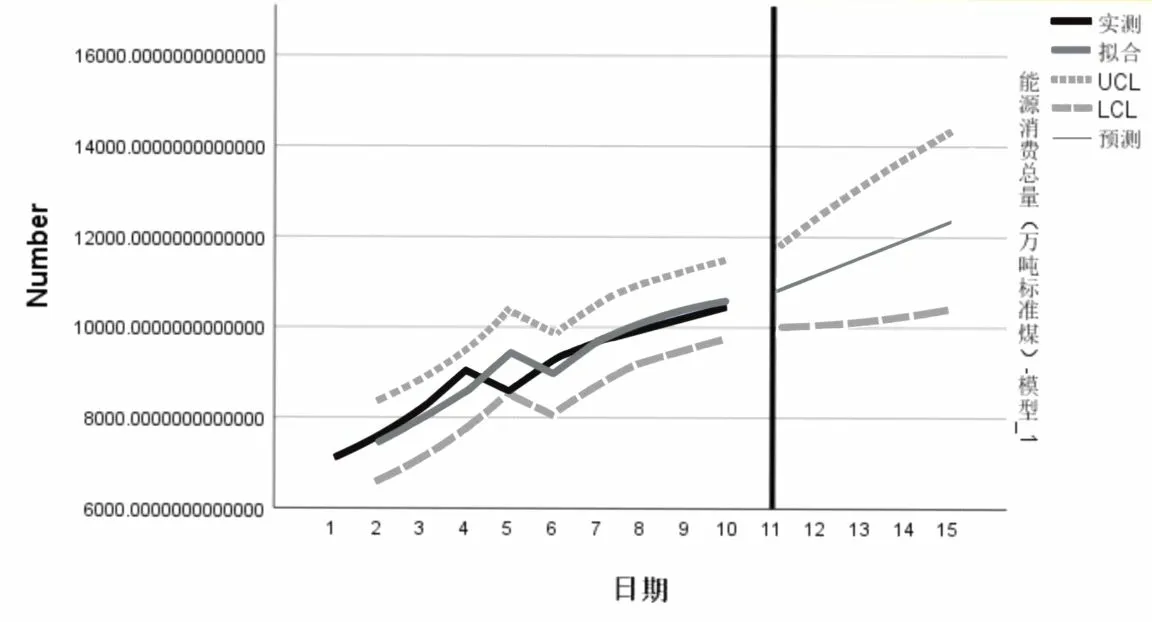
图3 ARIMA 模型的拟合和预测

（二）GM（1，1）模型的构建

选择贵州省2011—2020 年的能源需求数据，建立原始时间序列。其中是每年的能源需求。

（1）为了减少时间序列的随机性和波动性，先对原始序列进行累加得到新的序列其中

（2）根据灰色理论对X1建立关于t 的相应的微分方程为其中，“a”是GM（1.1）的发展系数，“b”是灰色作用量。用最小二乘法估计参数值：[a，b]T=（BTB）-1BTY。

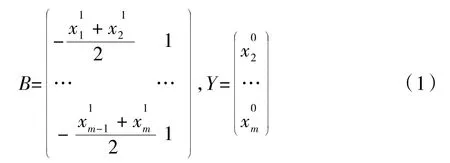
根据贵州省2011—2020 年能源消费的相关数据，可以得到。

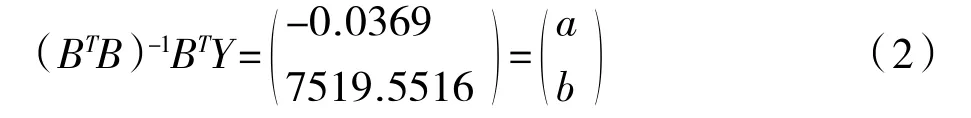
即a=-0.0369，b=7519.5516。

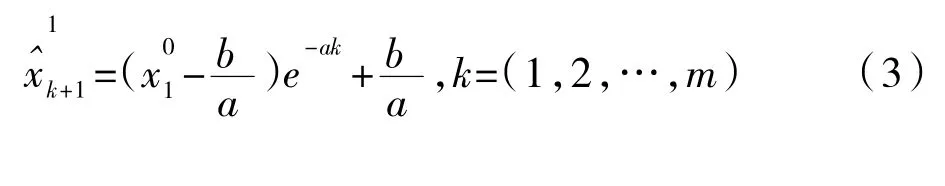
将上面的结果累减还原后，就可以得到GM（1.1）预测模型：

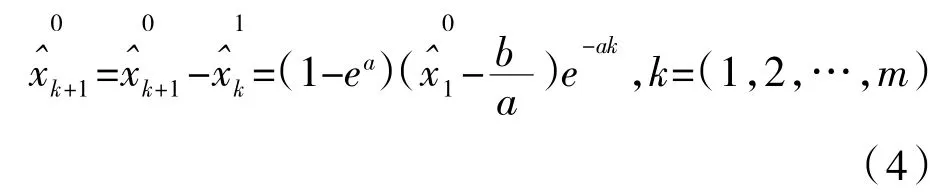
（3）模型的检验。灰色预测模型最常用的检验方式有两种：残差和后验差比。

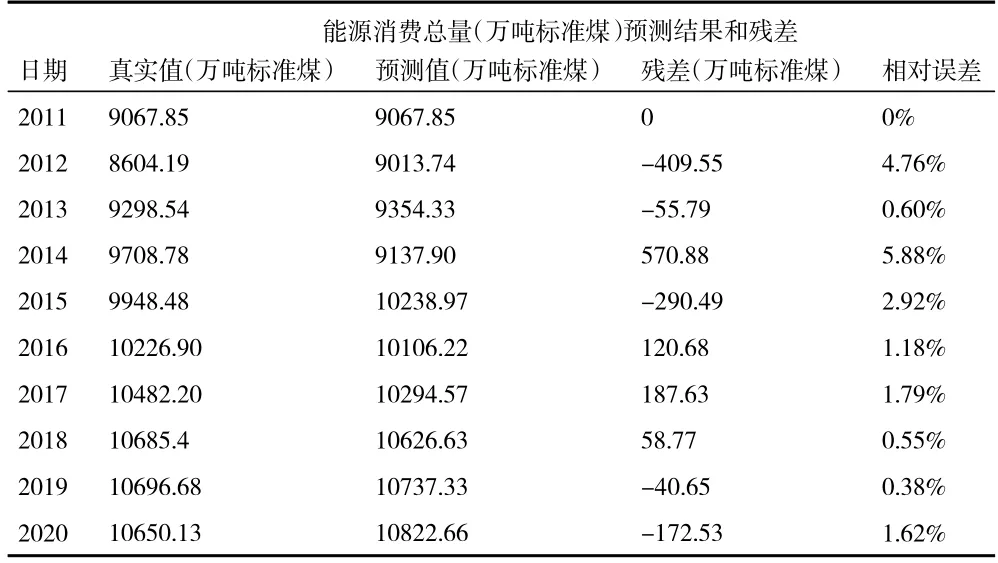
表3 GM（1,1）模型的拟合结果和残差

（三）GM-ARIMA 组合预测模型的构建

本文采用Shapley 值法来构建组合预测模型。该方法把单个预测模型的平均相对误差看作该模型对组合模型的贡献值，从而使多个模型之间成为合作关系。将预测的平均相对误差的总和视为这些模型的最大收益，通过最大收益的分配就可以确定组合模型中单个模型的权重[17]。

把ei设为第i 个单一模型预测的平均相对误差，则组合预测模型的最大收益即平均相对误差总值为E:

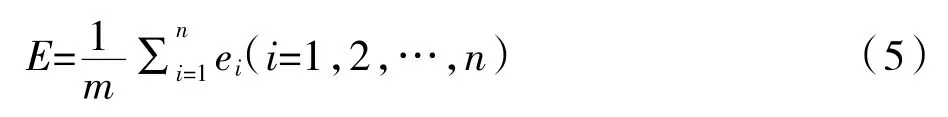
则基于Shapley 值法的第i 个模型所分配的平均相对误差值Ei:

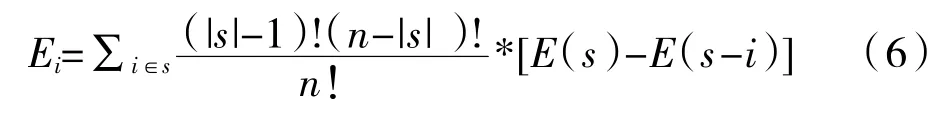
其中s 是n 个模型可能组成的集合且该集合中包含第i 个模型，|s|就是所组成的集合s 中模型的个数，E（s）是集合s 中所有模型组合后的平均相对误差值，E（s-i）是除去第i 个模型集合s 中剩余模型组合预测的平均相对相对误差值。然后可以得到第i 个预测模型在组合预测模型中的权重ωi：

则组合预测模型的预测值Y 为：

其中yi为第i 个模型的预测值。

四、结果讨论

从上文可以知道，ARIMA 预测模型的平均相对误差为2.697%，GM（1，1）预测模型的平均相对误差为1.968%。即e1=2.697%，e2=1.968%，根据公式（5）可以得到相对误差总值E=2.3325%。则ARIMA 预测模型和GM（1，1）预测模型所分配的Shapley 值分别为：E1=1.53075%，E2=0.80175%，然后再根据公式（7）可以得到ARIMA 预测模型和GM（1，1）预测模型分别在组合模型中所占的权重为：ω1=0.3437，ω2=0.6563。所以GM-ARIMA 组合预测模型的表达式为：Y=0.3437y1+0.6563y2。然后用GM-ARIMA 组合模型进行计算，结果如下表表4 所示。

从表4 计算得到GM-ARIMA 组合预测模型的平均相对误差为1.945%，低于ARIMA 预测模型和的平均相对误差2.697%和GM（1，1）预测模型的平均相对误差1.968%。由此可见，GM-ARIMA 组合预测模型的预测精度比两个模型分别预测的精度要高。所以可将组合模型用于对贵州省2021—2025 年的能源需求进行预测，预测结果如表5 所示。

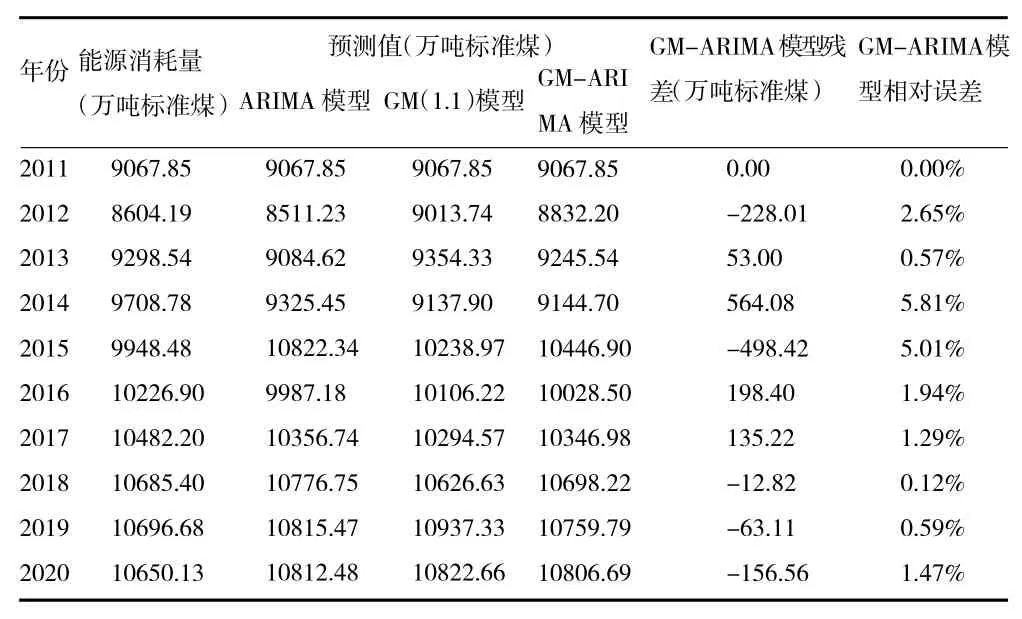
表4 GM-ARIMA 组合模型的预测结果和相对误差

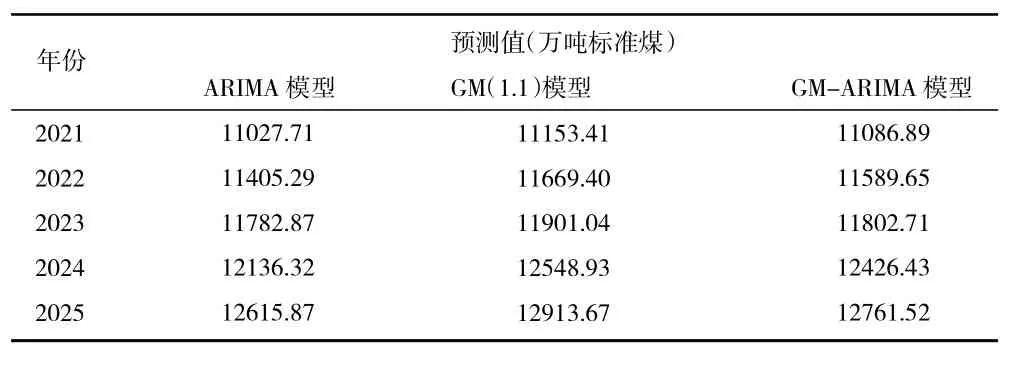
表5 贵州省2021—2025 年能源需求预测

五、结论与政策建议

从上文的分析可以得出，在三种模型中，ARIMA模型的误差率最高，GM（1，1）预测模型和GM-ARIMA组合预测模型的预测精度差不多，但是GM-ARIMA组合预测模型的相对误差要略低于GM（1，1）预测模型。GM-ARIMA 模型结合了这两种模型的优点，校正了预测结果并提高了准确性。因此采用GM-ARIMA组合预测模型预测能源消耗的结果是合理的。预测结果表明，贵州省的能源消费未来仍将呈现缓慢的增长趋势，贵州省2021—2025 年的能源需求将以年均3.6%的速度增长，截至2025 年，贵州省的能源需求将增长到2020 年的约119%。

为了适应日益增长的能源需求，政府应采取合理的政策措施。对此，提出了以下两条建议及措施：

（1）对于能源供给侧，应提高可再生能源的比例，例如风能、太阳能、水能、生物质能等，对于贵州省特殊的喀斯特地形来说，风能资源很丰富，所以更应大力推进风电的建设，逐渐降低不可再生能源的占比。由于煤炭资源在能源消费中占比最大，虽然消耗煤炭所产生的污染最大，但不能一刀切。应该提高煤炭资源的利用效率，即加大煤炭资源利用技术的投入和煤炭燃烧后污染物处理技术。

（2）对于能源利用侧，政府应该号召消费者节约能源，并制定能源消费的奖惩制度，即对于能耗高的企业采取提高能源消费税等惩罚方式，而对于能耗低的企业给予补贴等奖励方式。大力扶持高科技节能产业，鼓励能源利用技术的创新和碳减排技术的研发及应用。