基于火积耗散理论的并联热管传热特性仿真分析

张瑶瑶，张 伟，李 旭

（天津城建大学 能源与安全工程学院，天津300384）

热管是一种热阻小、运行稳定并且导热性能优异的传热元件[1]，热管被广泛地应用在工程、化工、电子、航空航天等众多领域中.重力热管作为热管的一种，其工作过程是通过工质的蒸发和冷凝实现热量的传递.工质在蒸发段液池内吸热汽化，由压差作用向上流动，通过上升管，流至冷凝段放热凝结成液体，在重力的作用下，通过下降管，重新流回蒸发段液池内，完成一个闭式循环.并联分离式重力热管作为一种置入到墙体的热管[2]可以充分利用被动式太阳能技术来降低建筑采暖能耗，既节约资源又不会对环境造成损害.

2006年过增元[3-4]基于导热与导电的比拟定义了一个描述物体传热能力的物理量——火积，而火积耗散理论上认为热量的传递消耗了热量的势能，即耗散了火积.陈群等[5]在火积定义的基础上，将火积耗散原理引入到传热问题的优化中.吴晶[6]将火积概念推广到辐射换热过程中的优化并提出了用于复杂边界条件下传热优化的最小加权热阻原理.Guo等[7]从传热学角度分析，认为火积耗散代表了传热过程中传热能力的损失及传热的不可逆程度.刘雄斌等[8]认为对于参与热工转换的换热器，熵产极值优化准则更合适，而对于加热、冷却系统的换热器，火积耗散极值优化准则相比于熵产极值更合适.由此可见，对于不涉及热工转换的物理过程而言，采用火积分析更适当.本文基于对火积的认识将其沿用到热管，来分析热管的传热过程.

根据热力学第二定律可知温差传热是不可逆过程.热量传递与电量传递过程相似，热量在温度差的驱动下传递，传递的量是守恒的，但是它们对应形式的能量（传递势能、电势能）是耗散的，是不守恒的.

除此之外，由于流体的黏滞性和通道表面粗糙度的存在，会造成传热过程的不可逆损失.该不可逆损失是无法用守恒量（如电量、热量）表示，而非守恒量（如电势能、传递势能）的耗散量才可以度量.因此，在控制单元格中的耗散率越大，则说明此处的不可逆损失越大.

随着CFD技术的发展，采用数值仿真方法分析热管内部的传热与流动特性的优势越来越明显.为了研究热管中热量的传递能力的损失程度以及热管传热过程耗散的分布，本文将火积耗散理论与CFD仿真方法相结合，利用自定义函数（UDF）将火积耗散模型加载到FLUENT中，对并联热管内工质的蒸发冷凝过程、热耗散特性以及热管的传热特性进行分析；确定热管传热过程的耗散特征，从而为热管传热特性的优化提供一条新的路径.

1 仿真模型以及火积耗散模型

1.1 控制方程

基于VOF模型的热管内气液二相介质流动传热控制方程[9]如下.

连续性方程为

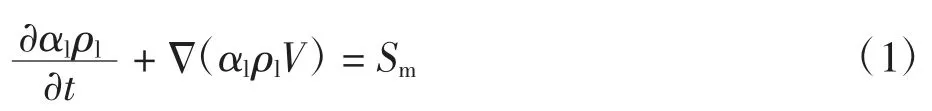
动量方程为

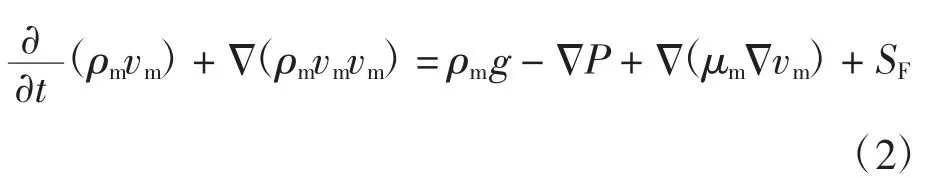
能量方程为

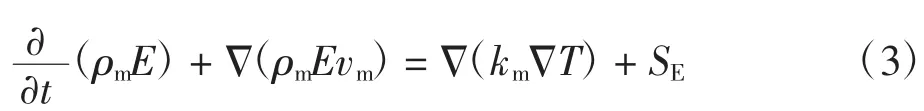
式中：αl为液相体积分数；ρl为液相密度；V为速度矢量；Sm为质量源项用于计算工质相变过程中质量的传递；SF为动量源项用于计算工质相变过程中动量的传递；E为内能；km为导热系数；SE为能量源项用来计算工质相变过程中能量的传递.

1.2 蒸发冷凝模型

重力热管高效的导热性主要是依靠内部工质气-液相变实现的，本文使用由Schepper等[10]提出的蒸发冷凝模型，并将其设置为源项加载到连续性方程和能量方程中.

在蒸发冷凝模型中，当T≥Tsat时，判定为蒸发过程，质量源项和能量源项如下

液相传质量方程为

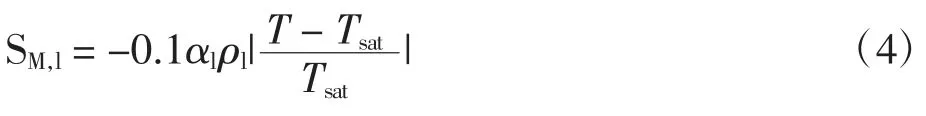
气相传质量方程为

蒸发过程中热量传递量方程为

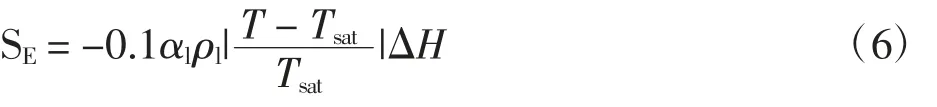
式中：Tsat为饱和温度；ΔH为气化潜热.

当T≤Tsat时，判定为冷凝过程，质量源项和能量源项如下.

液相传质量方程为

气相传质量方程为

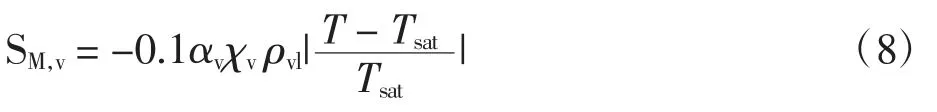
蒸发过程中热量传递量方程为

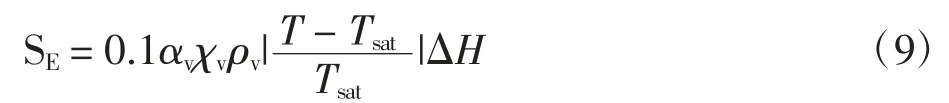
式中：χv为气相里液相的体积分数.

1.3 仿真模型与仿真设置

蒸发段和冷凝段由7根长210 mm、管径4 mm、管间距15 mm的并联管栅组成，如图1所示.其中：蒸发段支管的编号从左向右分别为LE1，LE2，…，LE7；同样，冷凝段支管编号从左向右分别为LC1，LC2，…，LC7；另外管栅的横管和热管的连接管管径均为10 mm.

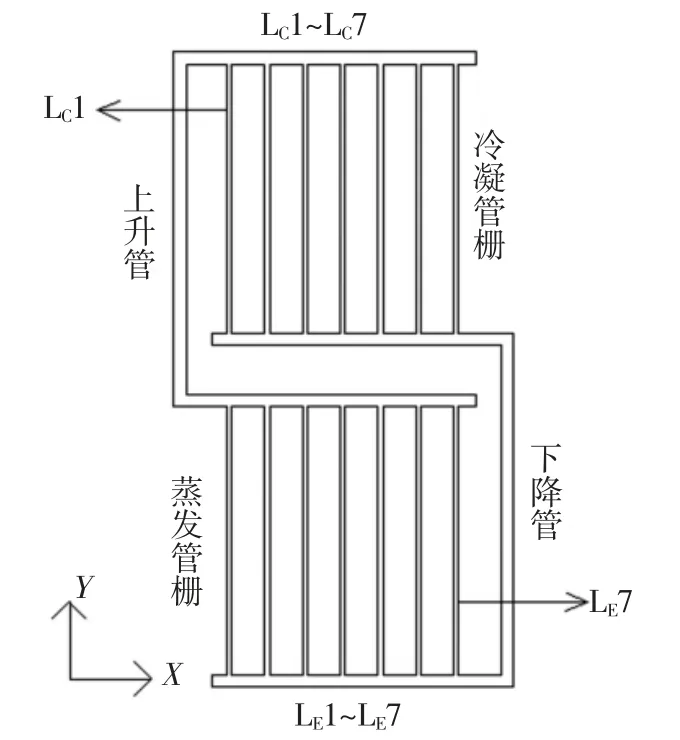
图1 并联分离式重力热管物理模型

热管的网格划分为结构化网格和非结构化网格两大类，结构化网格计算精确度更高，所以本文均使用结构化网格对模型进行计算，且网格质量都在0.95以上.因为流体存在黏性会在近壁面处形成边界层，所以需要在近壁面处对网格进行加密，边界层网格划分参数见表1，网格总数量为131 258个.

表1 热管边界层网格划分参数设置

本文热管材质选用玻璃，管中工质为液态水和气态水，在Fluent设置时，主相选为气态水，第二相选为液态水，气液两相间的表面张力作为源项加载到动量方程中，气液两相间的质量和热量传递选用UserDefined Functions用户自定义的方式作为源项加载到连续性方程和能量方程中.本文仿真计算采用结构化网格模型，动量求解采用一阶迎风离散格式，能量求解使用二阶迎风离散格式，时间步长取为0.001 s.

1.4 火积耗散计算模型

火积耗散理论认为热量的传递消耗了热量的势能，即耗散了火积.传递过程中的不可逆损失可以由耗散度量.因此，单位面积上耗散率越大，则说明此处的不可逆损失越大，反之亦然.

二维模型火积耗散率表达式[11-12]为

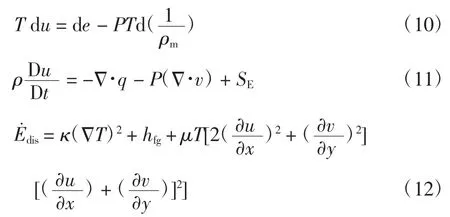
式（11）中：源项SE包括黏性耗散项和相变项.式（12）中：k为导热系数；为单位面积上的火积耗散率，表示单位面积热量传递能力的下降程度；等式右边第一项为传热项，第二项为相变项，最后一项为黏性耗散项.通过面积分即可得到有限面积上的火积耗散量Edis，其计算公式为

利用热管传热量Q和环境温度T0，可将火积耗散量无量纲化，得到无量纲火积耗散数NE，它来表示传热过程的不可逆程度，其计算公式为

在热管传热过程中，无论气相还是液相，其流速都较慢，以致于黏性耗散项所对应的火积耗散占总火积耗散比重很小（不足1%），故本文不考虑黏性耗散.传热耗散项以及相变耗散项所对应的火积耗散数计算公式如下

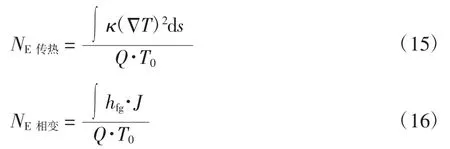
将上述火积耗散率表达式编译成C语言程序，利用UDF功能加载到Fluent每次的迭代计算中.在仿真计算开始前，设置好边界条件及初始条件，Fluent求解器就可以通过求解控制方程得到并联分离式重力热管的各物理量的分布，如速度、温度、体积分数等；然后，UDF就可以自行调用热管内的物理量进行耗散率的计算，还可以将火积耗散的分布以云图的形式输出，从而使得热管内各项不可逆损失可视化.

2 热管火积耗散分布和影响因素分析

火积耗散率、火积耗散数的物理意义如前所述，本文主要关注热管中工质火积耗散率、火积耗散数的分布特征以及加热功率对热管的影响，并在此基础上，探究传热和相变两种类型不可逆损失对热管传热性能的影响.

2.1 热管传热过程中火积耗散率及火积耗散数分布

研究过程中，每根210 mm的支管上每隔10 mm设置一个取值点，共设置22个取值点以便后续对热管支管及管栅的研究，布点情况如图2所示.

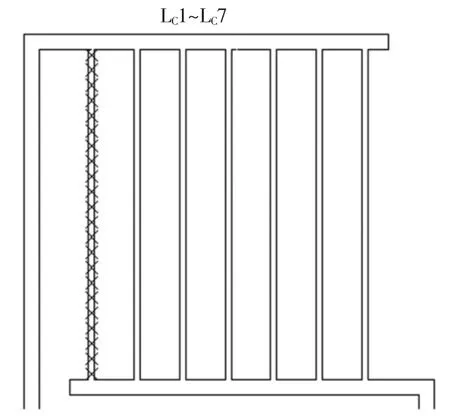
图2 支管布点

以加热功率70 W为例，研究热管中火积耗散分布，关于火积耗散数的仿真结果在表2中给出.从表中可以看出，在热管冷凝段处的不可逆损失中，由传热所造成的火积耗散数仅占2.35%，由相变造成的火积耗散数占到97.65%.因此可知，热管冷凝段的不可逆损失主要由相变造成，并且冷凝段内工质通过相变潜热传热产生的能质损耗大于显热传热的能质损耗.

表2 冷凝段火积耗散数

为进一步将热管的不可逆损失可视化，将热管冷凝段的火积耗散率以云图的形式来表示，即可更加清晰地观察到热管冷凝段传热耗散以及相变耗散的分布，如图3和图4所示.

图3 冷凝段传热火积耗散率

图4 冷凝段相变火积耗散率

从图3中可知，传热耗散率主要分布在支管LC3～LC7的下端.由式（12）火积耗散率的表达式可知，关于传热项的耗散率与温度梯度有关，冷凝段温度分布情况如图5-6所示.从图5温度分布图中不难发现，热管冷凝段的温度梯度较大部分发生在支管LC2、LC3的顶部，以及LC3～LC7的下半部分，与传热火积耗散率分布图相吻合.

图5 冷凝段温度分布云图

由图4中不难看出，相变火积耗散率主要分布在支管LC3～LC7的上半部分，这是因为这部分温度相对较低，低于气相工质的饱和蒸汽温度.工质在此处发生了冷凝，气相工质冷凝时，工质释放出的热量是潜热，工质的温度保持不变.而从图6可知，支管LC3～LC7上端的温度梯度趋近于零，气相工质在此处冷凝，与相变火积耗散率的分布图相对应.

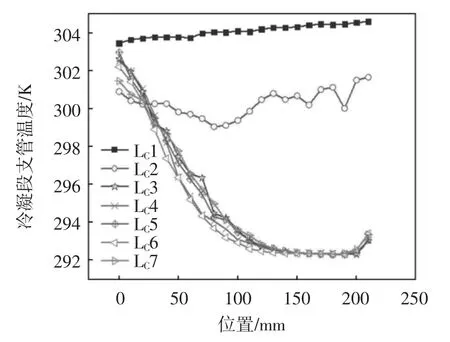
图6 冷凝段支管纵向温度分布

2.2 加热功率对热管火积耗散数的影响

加热功率对热管的传热能力有着重要的影响，加热功率过高会出现间歇沸腾，加热功率过低会引起热管不稳定振荡.火积耗散数随加热功率的变化以及分布情况如图7-8所示.

综合观察图7和图8不难发现，热管的传热火积耗散数不仅随加热功率的增加而增加，而且其占比也在升高，这是因为加热功率的增加会使蒸发段内的气相温度升高，扩大了气相与液相的温差，增加了蒸发段处的温度梯度，所以传热火积耗散数随之增加.当加热工率增加时，相变火积耗散却随之减小，这是因为加热功率的增加使得气相的温度升高，冷凝段中气相工质还未冷凝相变就已流出冷凝段，因此，相变火积耗散数随之减小.

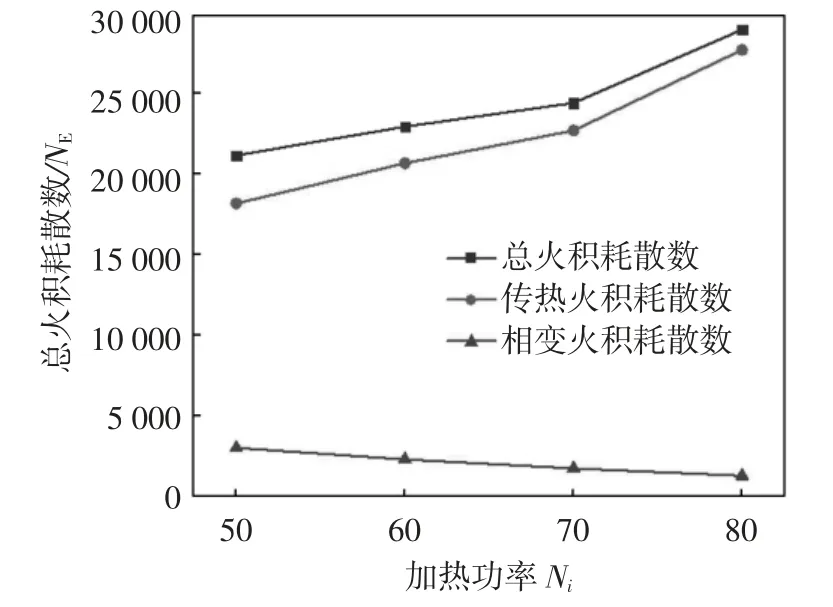
图7 火积耗散数随加热功率的变化曲线

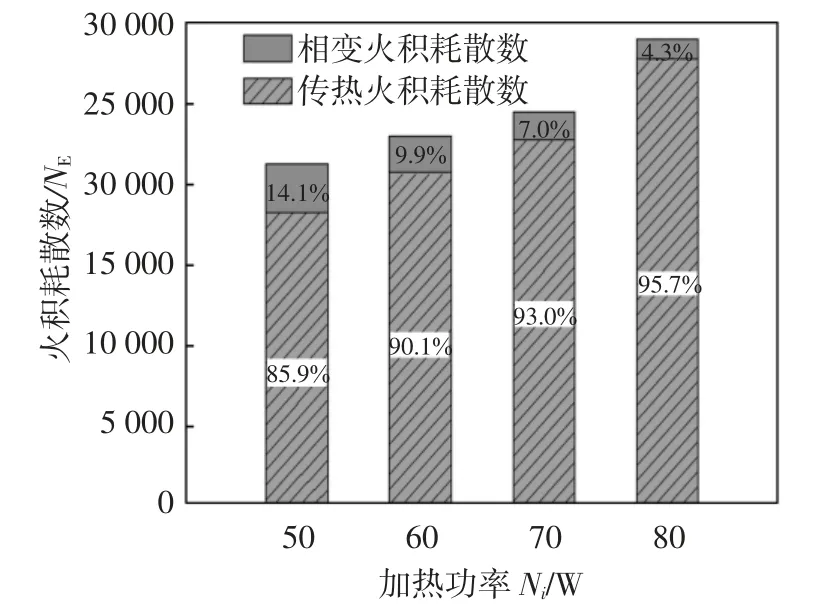
图8 各项火积耗散数占比

总之，不考虑黏性耗散的前提下，虽然相变火积耗散数随加热功率的增大而略有减少，但传热火积耗散数增大幅度更加明显.因此，两者共同作用下，随着加热功率的增加会使热管总火积耗散数增加，加热功率为50～80 W时，传热造成的不可逆损失占总损失的80%以上，还可以推测出传热火积耗散数的比重随加热功率增加而不断升高，是组成热管系统不可逆损失的主要部分；而相变所造成的不可逆损失约占总损失的20%以下，所占比重在随加热功率增加而不断下降.

3 结论

本文采用CFD仿真方法，研究了并联分离式重力热管中的不可逆损失，研究得出的主要结论如下.

（1）以加热功率Ni=70 W为例，将热管传热过程中不可逆损失可视化，分析得知：热管冷凝段内相变火积耗散数占冷凝段总火积耗散数的97.65%，而且集中分布在冷凝段支管LC3～LC7顶部；可知冷凝段内工质通过相变潜热传热产生的能质损耗大于显热传热的能质损耗.

（2）采用火积耗散理论对热管传热过程中不可逆损失进行分析，研究发现，在忽略黏性耗散的前提下，当加热功率增加时，相变火积耗散数逐渐减小，而传热火积耗散数逐渐增加，即热管的总火积耗散数与加热功率呈正相关.这表明随着加热功率的增加，热管内总体的不可逆程度增大.