拱形钢结构的自振特性及地震响应研究

窦宝峰 杨潇 窦超

拱形钢结构的自振特性及地震响应研究

窦宝峰1杨潇2，*窦超2

（1.临沂市建设安全工程质量服务中心，临沂 276000； 2.北京交通大学土木建筑工程学院建筑工程系，北京 100044）

作为一种典型的推力结构，拱形钢结构的动力特性和地震响应的影响因素众多，包括矢跨比、轴线形式、拱脚条件、结构形式（单拱、上承式拱、组拼拱）等自身参数，以及地震输入方向等地震动参数。为了揭示各因素的影响规律，本文基于数值计算分析，对拱形钢结构的自振特性和地震作用下的动力响应进行了参数化研究，总结了主要参数的影响规律。首先，对于钢拱的平面内振动和空间振动的自振特性，讨论了矢跨比、轴线形式、纵梁与拱肋刚度比、横撑刚度的影响。接着，针对地震作用下的钢拱结构，考察了地震输入方向、弹性拱脚对其位移和内力的影响规律。研究表明，矢跨比对钢拱平面内振动影响显著，矢跨比较大时水平振动明显；对于钢拱的抗震计算，一般应考虑水平纵向地震的影响，矢跨比较小时也应考虑竖向地震的影响；拱肋向内倾斜形成提篮拱可显著提高空间稳定性；拱脚弹性水平支承的钢拱由于推力结构受力特点削弱，在竖向地震作用下其受力更为不利。

拱形钢结构， 自振特性， 地震响应， 矢跨比， 弹性拱脚

0 引 言

拱形结构是一种将竖向荷载转化为截面轴向压力并由拱脚推力维持平衡的曲线构件。随着我国钢结构的迅速发展，拱形钢结构因其跨越能力大、造型优美等特点，在建筑结构和桥梁工程中得到广泛应用。

拱形钢结构不但要保证稳定承载力，还要在风、地震和车辆等动荷载作用下满足正常使用要求。关于拱形结构的动力问题，已有很多学者开展了研究，例如大跨度钢拱桥的风振响应［1-5］，考虑非线性影响下钢拱桥的地震响应［6-7］，也有专著并不单单针对拱形结构，而是全面探讨了桥梁结构所共通的问题，包括车—桥振动问题［8-9］和抗震设计［10-13］等。

本文重点对于拱形钢结构的自振特性和抗震性能进行分析，讨论各参数的影响规律，包括以下内容：①考察矢跨比、轴线形式、拱脚条件及结构形式等因素的影响，掌握拱形结构的振动特点；②通过对不同地震动参数和结构形式下（输入方向、提篮拱、水平弹性支承拱脚等）的地震响应进行分析，研究结构变形、内力及拱脚推力等变化规律。

参数化数值分析采用ANSYS有限元软件进行，钢拱、纵梁或横撑均采用梁单元BEAM188模拟，拱桥中的系杆采用杆单元LINK180模拟，拱脚弹性支承用弹簧单元Combin39模拟，简化起见质量源取为结构自重。计算中，所有构件均采用钢材，且不考虑材料弹塑性发展，即进行弹性分析，弹性模量=2.06 GPa，泊松比=0.3。为明确起见，如图1所示，本文将-平面即拱所在的竖向平面定义为“平面内”，其中沿着轴定义为“纵向”，沿着轴定义为“竖向”；而-平面即垂直于拱轴线平面的平面定义为“平面外”，沿着轴定义为“横向”。

图1　拱形结构示意

1 拱形钢结构的自振特性

1.1　平面内振动

拱形钢结构平面内的基本振型通常为反对称和对称两种形式。前者为整体水平纵向的振动，后者为竖直方向的振动。

矢跨比和拱脚推力是拱与梁系构件的重要区别，也是影响自振特性的主要因素。当矢跨比足够小时，拱与直梁类似，以竖向振动为主。随着矢跨比的增加，拱的竖向刚度增大，而水平刚度减小。与梁式结构比较，由于拱脚推力的作用，拱的竖向刚度显著加强。选取铰支圆弧拱，箱形截面□600×480×12×12 mm，跨度=30 m，变化矢跨比/=0～0.5，其平面内自振周期的计算结果如图2（a）所示，同时给出的还有相同条件下释放拱脚水平位移即无拱脚推力时的结果。可以看到：①在矢跨比0.10～0.50范围内，拱的竖向刚度大于水平刚度，小矢跨比时二者接近，矢跨比较大时水平振动明显；②无拱脚推力时的竖向振动周期远大于水平振动，可见拱脚水平推力极大地提高了拱的竖向刚度。③当矢跨比小于0.10时，随着矢跨比的进一步减小，拱的竖向刚度迅速降低，直至退化为直梁。

图2（b）所示为拱轴线形式对自振周期的影响，仍然选取两端铰支拱，箱形截面□600×480×12×12 mm，跨度=30 m，变化矢跨比/=0.01～0.5。结果表明，中小矢跨比时（/<0.30），圆弧拱和抛物线拱的自振周期接近；随着矢跨比的增大，抛物线拱的刚度逐渐高于圆弧拱。

图2　钢拱平面内自振周期的变化

图3（a）考察了铰支圆弧钢拱平面内振动的振型参与质量系数，计算时取矢跨比/=0.25，其他参数同上。振型参与质量系数反映了所考虑的各阶振型对结构动力响应的贡献率，一般规定其大于90%，这就要求计算时考虑足够阶数的振型结果。例如，《网格结构技术规程》（JGJ 7—2010）［14］中规定，对于网壳结构，由于其频率密集的特点，采用振型分解反应谱法进行地震作用分析时，至少要选取前25～30个振型。由图3（a）可见，对于钢拱平面内纵向水平振动，当参与计算的振型多于8个时，参与质量系数已经超过90%，其中第1、3、6、8阶振型对面内水平振动的贡献较大。因此认为选取前8阶自振模态结果进行后续地震响应计算，便可准确把握结构的动力反应。而对于竖直方向的振动，需至少考虑前12阶振型，其中第1阶、第6～11阶振型对竖向振动几乎没有贡献，而第2、4、5、12阶振型的贡献较大。图3（b）给出了不同矢跨比下（其他参数同上），参与质量系数达到90%时所需的振型阶数。可见随着矢跨比的增大，水平振动所需振型阶数逐渐减小，竖向振动所需振型阶数增加，这表明结构的水平方向振动愈加明显，占主导地位。

图3　拱平面内振动的振型参与质量系数

以上分析了单拱的平面内振动，对于由拱肋和纵梁组成的上承式、中承式或下承式拱桥，随着拱肋和纵梁二者刚度的比值不同，其在拱轴线平面内的振动模态将发生变化。以上承式拱桥为例，拱肋为箱形截面□600×480×12×12 mm，跨度=30 m，矢跨比/=0.25，纵梁距拱脚的高度为10 m。通过改变纵梁的截面抗弯刚度得到第一阶自振模态如图4所示，可以看到，当拱肋抗弯刚度较大时［图4（a）］，结构首先发生反对称形式的振动，实际工程中一般多为这种情况。当纵梁强而拱肋弱时［图4（b）］，将首先发生对称形式的竖向振动。

图4　上承式拱桥的振动

1.2　空间振动

当钢拱平面外没有足够支撑时，一般其面外刚度远小于面内刚度，因此第一阶自振模态为面外半波的弯扭变形，之后在高阶振型中面内振动和面外振动交替出现。随着结构形式以及面外与面内刚度比值的改变，其振动模态将有很大不同。

以带一字横撑的组拼拱进行说明，如图5所示。局部坐标系-的轴垂直于拱轴线平面，轴沿拱轴线的径向方向，轴沿拱轴线的切线方向。发生平面外弯扭变形时，与空腹桁架类似，横撑的线刚度和数目决定了平面外刚度的大小［9］。横撑的线刚度由横撑抗弯刚度与拱肋间距共同决定，而抗弯刚度又分为--平面内弯曲的EI和--平面内弯曲的EI。当拱肋截面发生绕-轴的扭转时，横撑将在--平面内产生弯曲，从而限制拱肋的扭转变形；另一方面，当拱肋有沿-轴的平面外侧移时，由于横撑在--平面的弯曲，带动拱肋发生局部弯曲变形，从而提高了结构的整体平面外刚度。

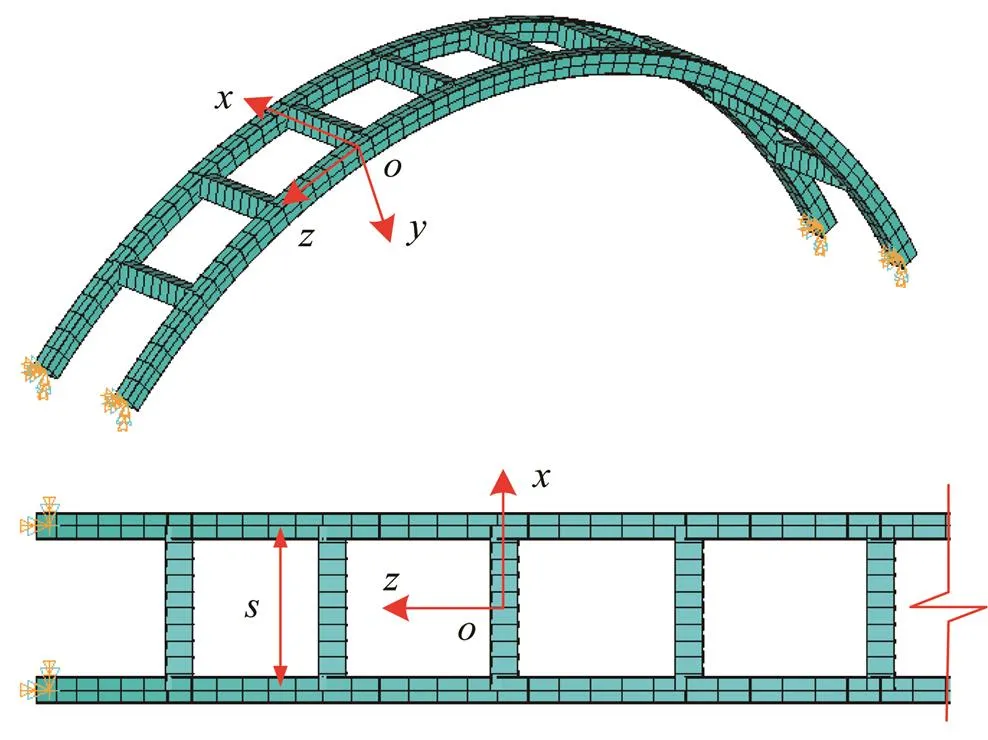
图5　带横撑的双肋拱结构示意

选取两端固支圆弧双肋拱，拱肋箱形截面尺寸□600×480×12×12 mm，矢跨比/=0.25，跨度=30 m，两拱的间距=/10=3.0 m。设拱肋截面在拱轴线平面内的抗弯刚度为EI，改变横撑的抗弯刚度：①令EI=EI，变化EI/EI=0.05～2.0；②令EI=EI，变化EI/EI=0.05～2.0。结构的第一阶自振频率结果如图6（a）所示。可以看到：①随着横撑抗弯刚度的增加，结构平面外刚度有所增强，但EI的影响明显大于EI的影响；②改变EI时，结构第一阶振型始终为平面外单波弯扭变形，而当EI≥1.15EI后，第一阶振型转变为平面内反对称变形。

图6（b）给出了结构自振频率随两个拱肋的间距的变化结果，一种情况是保持横撑在两个方向的抗弯刚度不变即EI=EI=EI/2，另一种情况是保持横撑的线刚度不变即EI/=EI/=5EI/。计算中不考虑横撑质量变化对自振频率带来的影响。结果表明，随着两拱间距的增大，第一种情况下由于横撑线刚度的减小，结构的自振频率迅速降低，而第二种情况下由于线刚度保持不变，因此自振频率变化不大。这进一步说明了在带横撑的组拼双肋拱中，在横撑布置一定时，横撑线刚度对结构平面外刚度起着决定性影响。

图6　带横撑的双肋拱结构的自振特性

当结构整体质量分布较为均匀时，结构的自振频率所反映出来的相对刚度大小，也从侧面反映了结构的稳定性高低，自振频率越高也就代表着结构的稳定性越好，因此稳定性能的影响因素和变化规律与动力特性有一定的相似性。

2 地震作用下拱形钢结构的动力响应

2.1　纵向和竖向地震动作用

对于拱形钢结构，沿着平面内水平纵向（即跨度方向）及竖直方向分别施加一致激励的地震作用，其产生的动力响应有很大差别，并随着矢跨比等因素的变化而变化。选取跨度30 m的铰支圆弧拱，箱形截面尺寸□600×480×12×12 mm，分别沿平面内纵向、竖向以及纵向和竖向双方向等三种方式输入北岭地震波（三种输入总加速度幅值均等于100 cm/s2），考察三种输入下的结构响应。

图7　纵向和竖向地震引起的钢拱动力响应

图7以地震动引起的拱肋截面最大内力或正应力为指标，来确定地震影响占主导的输入方向。其中纵坐标为沿纵向或竖向地震输入时拱中的最大响应（轴力、弯矩或截面正应力），与沿纵向和竖向双方向输入时最大响应之比。结果表明：①从弯矩来看，纵向地震的影响远大于竖向地震；②就轴力而言，中小矢跨比时竖向地震的影响大于纵向地震，而当矢跨比/>0.35时相反；③拱截面最大正应力结果反映了弯矩和轴力的共同影响，竖向地震引起的最大正应力远小于纵向地震。因此对于钢拱的抗震计算，一般应考虑纵向地震的影响，矢跨比较小时（如/≤0.15）竖向地震的影响也不能忽略。

2.2　横向地震动作用

在垂直于拱轴线平面的横向地震作用下，拱肋主要承受面外弯矩作用，拱顶的加速度反应最大，而内力峰值则出现在拱脚附近，并且响应一般要比纵向地震波作用下大很多［10］。建筑结构中的钢拱一般在平面外受到屋面板、拉杆、檩条等次构件的约束，能有效降低横向地震反应。而在大跨度体育场和桥梁结构中，多采用带风撑的组拼拱的结构形式，以此增大结构的面外刚度，减小横向地震响应。组拼拱的两拱肋也可内倾形成“提篮拱”（一般倾斜角度为10°左右为宜［15］），进一步增加空间稳定性［图8（b）］。下面针对带有一字横撑的平行拱肋组拼拱以及提篮拱，分析其在横向地震作用下的动力响应，计算中暂不考虑吊杆和桥面板等部件的影响。

图8　带风撑的双肋组拼拱

算例参数如下：两端固支圆弧拱，跨度=100 m，矢跨比/=0.25，两拱肋的拱脚间距=16 m，拱肋与横撑均为箱形截面□1200×1 000×30×50 mm，沿拱轴线长度均匀设置5段一字横撑，端部与拱肋刚接。提篮拱的两拱肋在拱顶处间距为8 m，拱肋向内倾斜9°。选取上节的Emeryville地震波时程，沿横向输入，加速度幅值为100 cm/s2，考察结构的地震反应。

图9（a）给出了平行双肋拱和提篮拱的自振周期比较，可见提篮拱由于拱肋的内倾，提高了结构的面外刚度，特别是第一阶自振周期（面外侧向振动）减小约27%。图9（b）所示为两种组拼拱在横向地震作用下拱顶面外侧向位移的时程曲线。拱肋和横撑中的轴力、弯矩及正应力的最大响应见表1，其中括号内的数值为提篮拱相比平行双肋拱的变化率。可以看到，在横向地震作用下，拱肋的最大轴力、弯矩和正应力均出现在拱脚截面，一字横撑中动力响应的最大值出现在拱顶的横撑端部。拱肋向内倾斜形成提篮拱后，拱顶侧移、拱肋和横撑中内力峰值均比平行双肋拱大大减小。

表1　 双肋组拼拱的地震响应最大值

图9　双肋组拼拱的动力特性和地震反应

2.3　弹性拱脚的影响

通常拱形钢结构的拱脚条件并非理想的固支或铰支，例如建筑结构中钢拱常落于下部弹性支承结构之上（图10），在推力作用下拱脚将有一定的水平位移。此时由于拱脚水平弹性支承的影响，地震作用下结构响应将与理想水平刚性支承的情况存在一定差异。

图10　水平弹性支承钢拱示意

图10采用刚度为的弹簧来模拟拱脚水平弹性支承的情况，令水平弹性刚度=αEI/3，其中EI为钢拱截面抗弯刚度，为拱轴长度，为刚度系数。选取两端铰支圆弧拱，箱形截面□600×480×12×12 mm，跨度=30 m，矢跨比/=0.25。图11（a）为拱顶集中荷载作用下线弹性静力分析得到的拱脚水平推力随水平弹性刚度的变化情况，纵坐标为弹性支承时的拱脚推力与刚性支承时的比值。竖直虚线对应的水平弹性刚度系数=250，对应的拱脚推力为刚性支承时的75%。图11（b）给出了在此水平弹性刚度（=250）下钢拱的自振周期，可见支承刚度的削弱大幅提高了前几阶自振周期。

图11　弹性支承钢拱的受力特性

选取Emeryville地震时程，沿纵向和竖向双方向同时输入，两个方向加速度幅值之比为1∶0.65（纵向最大加速度幅值为100 cm/s2），考虑刚性支承和水平弹性支承=250的两种情况。从图12计算结果可以看到，随着拱脚支座水平支承刚度的降低，拱顶竖向位移以及拱内截面最大正应力显著增大。究其原因，对于拱形结构正是由于拱脚推力的作用，其平面内弯矩和竖向变形远小于相同参数下无推力结构。拱脚支座水平支承刚度的减小，削弱了推力结构的受力特征，导致拱承载效率的下降。

图12　弹性支承钢拱的地震响应

3 结 论

本文通过探讨影响拱形结构振动的主要因素以及分析不同地震动参数和结构形式下的动力响应规律，得到如下结论：

（1） 对于拱的平面内振动，矢跨比较大时水平振动明显，随着矢跨比的减小（<0.10），拱的竖向刚度迅速降低，竖向振动显著。

（2） 随着矢跨比的增大，钢拱进行水平振动响应分析时达到振型参与质量系数要求所需的振型阶数逐渐减小，竖向振动响应分析所需的振型阶数增加。

（3）对于钢拱的抗震计算，一般应考虑纵向地震的影响，矢跨比较小时也应考虑竖向地震的影响。

（4）在横向地震作用下，当拱肋向内倾斜形成提篮拱后，拱肋、横撑的内力以及拱顶面外侧移变形均比平行双肋拱大大减小，提高了空间稳定性。

（5）钢拱采用水平弹性支承后，能够减小水平地震动的影响，但由于推力结构受力特点削弱，在竖向地震作用下其受力尤为不利。

［1］邓宇.大跨度拱桥涡致振动试验研究［D］.重庆：重庆大学，2005.

Deng Yu.Experimental study on vortex-induced vibration of long-span arch bridges［D］.Chongqing：Chongqing University，2005.（in Chinese）

［2］王承启.大跨度钢桁架拱桥风振研究［D］.重庆：重庆大学，2011.

Wang Chengqi.Wind-induced vibration of long-span steel truss arch bridge［D］.Chongqing：Chongqing University，2011.（in Chinese）

［3］王军泽.大跨度钢桁架拱桥风致振动试验与仿真研究［D］.长沙：湖南大学，2016.

Wang Junze.Wind-induced vibration test and simulation of long-span steel truss arch bridge［D］.Changsha：Hunan University，2016.（in Chinese）

［4］邹岩.铁路大跨度钢桁梁加劲拱桥风致振动研究［J］.铁道建筑技术，2017（4）：61-65，69.

Zou Yan.Research on wind induced vibration of railway long-span steel truss girder stiffened arch bridges［J］.Architectural Technology，2017（4）：61-65，69.（in Chinese）

［5］李先进，卿仁杰，朱强，等.三主桁式大跨度钢拱桥气动力特性与风振性能研究［J］.铁道科学与工程学报，2020，17（3）：628-636.

Li Xianjin，Qing Renjie，Zhu Qiang，et al.Study on aerodynamic characteristics and wind-induced performance of long-span steel arch bridge with three main truss［J］.Journal of Railway Science and Engineering，2020，17（3）：628-636.（in Chinese）

［6］赵灿晖，周志祥.大跨度上承式钢桁拱桥的地震响应分析［J］.铁道科学与工程学报，2006，（5）：6-11.

Zhao Canhui，Zhou Zhixiang.Analysis of seismic response of long-span overhead steel truss arch bridge［J］.Journal of Railway Science and Engineering，2006，（5）：6-11.（in Chinese）

［7］梁正裕，陈艾荣.考虑双非线性影响的大跨度上承式钢拱桥地震响应研究［J］.振动与冲击，2009，28（11）：139-145，209-210.

Liang Zhengyu，Chen Airong.Seismic response of long-span steel arch bridge considering double nonlinear effects［J］.Vibration and Impact，2009，28（11）：139-145，209-210.（in Chinese）

［8］项海帆，刘光栋.拱结构的稳定与振动［M］.北京：人民交通出版社，1991.

Xiang Haifan，Liu Guangdong.Stability and vibration of arch structures［M］.Beijing：People's Communications Press，1991.（in Chinese）

［9］李国豪.桥梁结构稳定与振动［M］.北京：中国铁道出版社，1992.

Li Guohao.Stability and vibration of bridge structures［M］.Beijing：China Railway Press，1992.（in Chinese）

［10］范立础，胡世德，叶爱君.大跨度桥梁抗震设计［M］.北京：人民交通出版社，2001.

Fan Lichu，Hu Shide，Ye Aijun.Seismic design of long-span bridges［M］.Beijing：People's Communications Press，2001.（in Chinese）

［11］范立础，卓卫东.桥梁延性抗震设计［M］.北京： 人民交通出版社，2001.

Fan Lichu，Zhuo Weidong.Ductility seismic design of bridges［M］.Beijing：People's Communications Press，2001.（in Chinese）

［12］范立础，王志强.桥梁减隔震设计［M］.北京： 人民交通出版社，2001.

Fan Lichu，Wang Zhiqiang.Design of Bridge Isolation and Reduction［M］.Beijing：People's Communications Press，2001.（in Chinese）

［13］陈惠发，段炼.桥梁工程抗震设计［M］.北京： 机械工业出版社，2008.

Chen Huifa，Duan Lian.Seismic design of bridge engineering［M］.Beijing：China Machinery Industry Press，2008.（in Chinese）

［14］中华人民共和国住房和城乡建设部.JGJ 7—2010 空间网格结构技术规程［S］.北京：中国建筑工业出版社，2010.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China.JGJ 7—2010 Technical specification for space frame structures［S］.Beijing：China Building Industry Press，2010.（in Chinese）

［15］陈宝春.钢管混凝土桥［M］.2版.北京：人民交通出版社，2007.

Chen Baochun.Concrete-Filled Steel Tubular Bridges ［M］.2ndEdition.Beijing：People's Communications Press，2007.（in Chinese）

Dynamic Characteristic and Seismic Response of Arch Structures

DOUBaofeng1YANGXiao2，*DOUChao2

（1.Linyi Construction Safety Engineering Quality Service Center， Linyi 276000， China；2.Department of Structural Engineering，School of Civil Engineering，Beijing Jiaotong University， Beijing 100044， China）

As a typical thrust structure，the dynamic characteristics and seismic response of arch steel structure are affected by many factors，including rise-span ratio， axis form， arch foot condition， structure form （single arch，upper bearing arch，assembled arch），and other parameters of ground motion， as well as seismic input direction，and so on.To reveal the influences of various factors， based on numerical calculation and analysis，the natural vibration characteristics and dynamic response of arch steel structures under earthquake are parameterized， and the influence rules of main parameters are summarized. First， for the free vibration characteristics of in-plane vibration and spatial vibration of steel arch， the effects of rise-span ratio， axis form， longitudinal beam to arch rib stiffness ratio，and transverse brace stiffness are discussed. Then， aiming at the steel arch structure under earthquake，the effects of seismic input direction and elastic arch foot on its displacement and internal force are investigated.The study shows that the rise-span ratio has a significant influence on the in-plane vibration of steel arch， and the horizontal vibration is obvious when the rise-span ratio is large； for the seismic calculation of steel arch，the influence of longitudinal earthquake should be considered， and the influence of vertical earthquake should also be considered when the rise-span ratio is small； the basket handle arch formed by the inward inclination of arch ribs can significantly improve the spatial stability. Due to the weakening of the horizontal thrust of the arch foot， the force of the steel arch is more disadvantageous under a vertical earthquake.

arched steel structure， natural vibration characteristics， seismic response， rise-span ratio， elastic arch foot

2021-02-20

窦宝峰，副高，从事钢结构抗震研究。E-mail： dbf06@qq.com

联系作者：杨 潇，女，硕士，从事钢结构抗震研究。E-mail： 1256884770@qq.com