约束最小二乘滤波的高斯模糊图像复原研究

张艳红 覃凤清 姜 丽 文兴东 何文杰 万浩飞

约束最小二乘滤波的高斯模糊图像复原研究

张艳红 覃凤清 姜 丽 文兴东 何文杰 万浩飞

（宜宾学院，四川 宜宾 644000）

文章分析了两种常见的图像复原滤波的复原原理及其局限后，在已知图像退化函数的情况下，主要对高斯模糊图像分别进行维纳滤波和约束最小二乘法滤波复原处理并比较这两种处理效果图像的优劣之处，在上述基础上，重点是分析不同高斯点扩展函数的尺寸及标准差的参数对高斯模糊图像复原效果的影响。最后再综合视觉效果和PSNR值得出高斯模糊图像使用约束最小二乘滤波复原的效果较佳，并且在真实高斯点扩展函数参数附近的参数复原效果会更好。

高斯模糊；图像复原；约束最小二乘滤波；维纳滤波；点扩展函数

引言

图像复原算法有很多种，主要包含非盲复原算法和盲复原算法两类。最早的是Harris提出使用点扩散函数模型来处理由于大气干扰引起的模糊图片，随后相继提出了逆滤波、维纳滤波、约束最小二乘滤波等非盲复原算法[1]。图像复原首先要有一个明确的图像复原质量准则，处理时需要对图像退化过程先进行估算，并且补偿退化过程造成的失真，以便获得未经干扰退化的原始图像或原始图像的最优估值[2]，衡量与原始场景图像的接近程度。上述问题的关键在于复原模型的建立，复原模型必须根据引起图像退化的数学模型对退化图像进行处理，然后通过学习建立它们之间的映射关系，从而对高分辨率图像进行引导和估计，复原丢失的信息，进而达到恢复图像的目的。实际运用可以使用不同滤波的手段对同一个图像进行图像复原处理，使复原后图像符合一定的视觉标准，进而达到复原图像的目的。

本文主要解决高斯模糊图像复原的问题，高斯模糊是生活中常见的模糊图像，解决此类图像的模糊问题可以使后续应用更加方便和高速。文中首先介绍了高斯模糊图像的退化模型，然后研究了维纳滤波和约束最小二乘滤波的复原原理和局限性，然后通过上述两种不同复原算法对高斯模糊图像进行处理，得出处理高斯模糊图像较好的复原算法。最后，分析了不同高斯点扩散函数的大小和标准差参数对高斯模糊图像恢复的影响，并得出了相应的结论。

1 高斯模糊

1.1 高斯图像退化模型

图像模糊是由于像素值的局部平均化而导致图像内容的平滑[3]，在图像的成像过程中，目标会高速运动、散射、成像系统畸变和噪声等干扰，使最终的图像出现很多问题，称为“退化”。图像复原的关键是建立退化模型[4]，通常，使用一致的数学模型来描述图像退化过程，然后建立退化模型。对模型进行精确处理，然后反向推导，确定复原图像复原的准确性。然后，将图像降晰过程抽象化，粗略概括为将高清图像与未知点扩展函数进行卷积，并加入噪声，最终得到降晰图像。

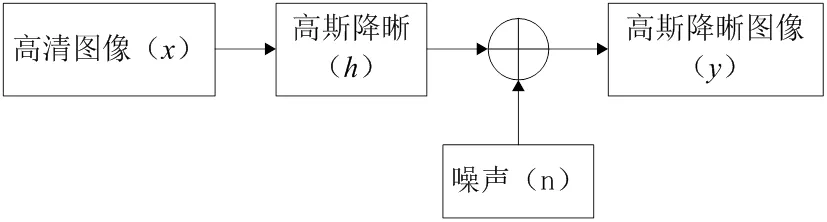
图1 高斯图像退化模型

2 图像复原处理算法

2.1 维纳滤波

常见的图像复原处理包括维纳滤波处理、逆滤波处理、约束最小二乘滤波处理等复原算法，在这些复原方法中，维纳滤波的图像复原处理是一种常见的滤波器，是去除退化图像的模糊和噪声的理想滤波器[6]，被广泛应用于各种图像检测处理。在Wiener（维纳）滤波图像复原中，中和了退化函数和噪声统计这两个方面来进行图像的复原处理。

维纳滤波复原的主要原理是假设图像噪声是一个随机过程，找到一个没有失真图像的估值，使得它们之间的均方误差达到最小，从而实现图像复原的效果。在图像复原过程之中，实际使用到的是非因果Wiener（维纳）滤波器，因为它的频域形式比较简单，计算效率比较高[7]。

维纳滤波是一种线性图像复原方法，寻找一个使统计误差函数：

在频域可以表示为：

2.2 约束最小二乘滤波

其约束条件为：

从公式中可以看到，约束最小二乘滤波在高频区域中信噪比较低，但是由于通常噪声是出现在高频部分，所以滤波器在抑制噪声的同时也会过滤掉一些图像本身就有用的高频信息，这说明约束最小二乘滤波在滤波复原过程中，可以减少对噪声的放大作用[10]，从而达到图像复原的效果。对于不同原始图像的先验知识，采取克服模糊的不同方案，约束最小二乘解具有不同的具体形式。约束最小二乘算法对噪声较为敏感，在无噪声或可以忽略的情况下可以获得比较理想的复原效果[11]。

3 高斯点扩展函数

图像模糊的成因有成像系统的像素差、有限宽带造成的图像失真、模拟图像数字化过程中，由于损失掉部分细节，因而造成图像质量下降等问题。在现实生活中，很多光学测量和成像系统的降晰函数均趋近于高斯点扩展函数（PSF），如显微镜成像系统、光学相机都属于高斯型。

通常，高斯点扩展函数表示为如下形式：

其中Sup表示支持域，通常被表示为一个K*K的矩形区域、K被称为高斯点扩展函数的尺寸，通常是3～15的奇数、σ为高斯点扩展函数的标准差。因此，高斯模糊图像主要改变的是高斯点扩展函数的尺寸和标准差。

4 实验及对比

为了更好地验证约束最小二乘滤波对高斯模糊图像的复原效果，实验是通过对Lena原始图像如图2（尺寸为256×256）加以高斯点扩展函数的尺寸为9、标准差为3时生成的高斯模糊图像如图3所示，高斯模糊图像的PSNR值为31.6277 dB，通过对高斯模糊图像分别使用维纳滤波和约束最小二乘滤波复原处理，进而比较出约束最小二乘滤波与维纳滤波的复原效果的差异，接着再研究不同高斯点扩展函数的参数对复原效果的影响。

图2 原始图像

图3 高斯模糊

4.1 不同复原算法的复原效果比较

为了评价不同复原算法的复原效果，在原始高斯点扩展函数参数情况下进行复原。此时高斯点扩展函数估计尺寸为9、标准为3，通过维纳滤波及约束最小二乘滤波算法进行图像复原，所得到复原图像及图像PSNR值如图4、图5所示。

（PSNR：27.1937 dB）

（PSNR：33.4747 dB）

通过这组对比实验可以看出对于高斯模糊图像，进行维纳滤波和约束最小二乘法滤波复原处理后，从复原图像质量以及客观评价标准来看，约束最小二乘滤波复原的效果比维纳滤波复原效果好，细节保持能力较优，因此对于高斯模糊图像，应更多使用约束最小二乘滤波复原方法。

4.2 高斯点扩展函数参数对复原图像质量的影响

通过改变高斯点扩展函数的参数（即高斯点扩展函数的尺寸及标准差）对同一模糊图像进行约束最小二乘法滤波复原处理，并对这几组数据进行比较，分析高斯点扩展函数参数对复原图像质量的影响。

4.2.1 高斯点扩展函数尺寸对复原图像质量的影响

为了验证高斯点扩展函数尺寸参数对复原图像质量的影响，当高斯点扩展函数的标准差为3时，在尺寸分别为5、7、11、13时通过约束最小二乘滤波进行图像复原，得到的图像如图6所示，复原图像的PSNR值见表1。

图6 不同尺寸的复原图像

表1 不同尺寸复原图像的PSNR值

高斯点扩展函数尺寸PSNR（dB） 530.8912 729.8729 933.4747 1128.8632 1328.7225

图7 不同尺寸复原图像的PSNR值

通过图7及PSNR值可以看出在高斯点扩展函数的标准差一定的情况下，改变高斯点扩展函数的尺寸对图像复原质量的影响是明显的。当高斯点扩展函数的尺寸逐渐接近原始尺寸时复原效果会越来越好，PSNR值逐渐在增大，一旦到达原始尺寸后，接着增加数值图像复原效果会逐渐下降。

4.2.2 高斯点扩展函数标准差对复原图像质量的影响

为了验证高斯点扩展函数标准差参数对复原图像质量的影响，当高斯点扩展函数的尺寸为9时，在标准差分别取2、2.5、3.5、4时通过约束最小二乘滤波进行图像复原，得到的图像如图8所示，复原图像的PSNR值见表2。

图8 不同标准差的复原图像

表2 不同标准差复原图像的PSNR值

高斯点扩展函数标准差PSNR（dB） 230.3736 2.529.2014 333.4747 3.529.8002 428.7415

图9 不同标准差复原图像的PSNR值

通过图9及PSNR值可以看出在高斯点扩展函数的尺寸一定的情况下，改变高斯点扩展函数的标准差得到不同的图像。当高斯点扩展函数的标准差逐渐接近原始标准差时效果会越来越好，当达到原始标准差时，再增加标准差复原效果不会很明显。因此，要想得到更精确的复原结果，高斯点扩展函数的参数取值还需进一步深入研究。

5 结束语

图像复原技术与其他基本图像处理技术相类似，都是一种以获取视觉效果在某个方面提升为目的，是图像处理领域中一种非常重要的技术。文中通过对上述两种不同算法的研究分析及对计算机模拟出的高斯模糊退化图像进行复原处理，从复原图像质量以及客观评价标准来看，得到约束最小二乘滤波复原处理能更好的复原高斯模糊图像，在此基础上改变高斯点扩展函数参数时越靠近真实值图像复原效果越好这一结论。此外对于不同的模糊图像对应的最佳复原方法均不同，后续需要在复原方法的参数估值方面研究，更重要的是对算法的深入研究。

[1] 李亚成. 高斯模糊图像复原与匹配算法研究[D]. 武汉: 华中科技大学，2019.

[2] 黄力宇，黄登凤，张园. “医学影像处理”课程实验软件的开发[J]. 电气电子教学学报，2012，34(6): 82-84，109.

[3] 张墨华. 基于先验学习的图像复原技术研究[D]. 郑州: 战略支援部队信息工程大学，2019.

[4] 王鹏飞. 运动模糊图像复原算法研究[D]. 重庆: 重庆大学，2013.

[5] 谢盛华，张启衡，宿丁. 基于APEX方法的改进图像复原算法[J]. 激光与红外，2007(2): 185-188.

[6] 陈树越，朱双双，蒋星，等. 基于高斯型点扩展函数的红外图像热源复原[J]. 激光技术，2016，40(2): 270-273.

[7] 李慎之. 毫米波无源成像超分辨算法研究及DSP实现[D]. 成都: 电子科技大学，2011.

[8] 刘书君. 运动模糊图像复原技术研究[J]. 信息通信，2017(4): 4-5.

[9] 万宇. 空间变化模糊的图像复原算法[D]. 杭州: 浙江工业大学，2018.

[10] 李国立，段汕. 基于约束最小二乘数字图像恢复[J]. 电脑知识与技术，2008(14): 914，925.

[11] 石明珠. 运动模糊图像全变分复原理论及关键技术研究[D]. 北京: 北京理工大学，2014.

Research on Gaussian Blur Image Restoration Based on Constrained Least Squares Filtering

After analyzing the restoration principles and limitations of two common image restoration filters, this paper mainly performs Wiener filtering and constrained least square filtering restoration on Gaussian blur image respectively when the image degradation function is known, and compares the advantages and disadvantages of these two processing effects. On the basis of the above, the emphasis is to analyze the influence of the size of different Gaussian point spread functions and the parameters of standard deviation on the restoration effect of Gaussian blur image. Finally, combining the visual effect and PSNR value, it is found that the effect of Gaussian blur image restoration using constrained least square filter is better, and the parameter restoration effect near the parameters of the real Gaussian point spread function is better.

Gaussian blur; image restoration; constrained least squares filtering; Wiener filter; point spread function

TN911

A

1008-1151(2022)09-0010-04

2022-07-10

四川省教育厅项目（18ZA0538）；宜宾市科技局项目（2017ZSF009-9）；宜宾学院科研项目（2020YY02）；国家级大学生创新项目（202010641021、201910641016）；四川省大学生创新项目（S201910641096、S202010641126）；宜宾学院大学生创新项目（X106412020336）。

张艳红（1999－），女，安徽阜阳人，宜宾学院学生，研究方向为数字图像处理。

覃凤清（1976－），女，四川南充人，宜宾学院研究员，博士，研究方向为数字图像处理。