X舵水下潜航器改进滑模控制策略研究

刘 胜，段应坤，张 晶

(1.哈尔滨工程大学， 哈尔滨 150001； 2.中船黄埔文冲船舶有限公司， 广州 510715)

1 引言

随着海洋工程的发展，各式各样的水下潜航器开始被广泛应用于海洋探索和海洋资源开发。自主水下航行器(autonomous underwater vehicle,AUV)作为重要的海洋装备，在水下检测和海洋探索的地位越来越重要。

自主式水下潜航器(AUV)作为独立的自主智能系统，可以在水下独立完成各项复杂任务。但由于海洋环境的复杂性，这便要求AUV具有稳定可靠的水下航行性能。X舵AUV由于改进了其尾部操纵面，大大提高流了其在水下的可操作性及水动力性能，X舵AUV其方向舵在AUV的船首和船尾形成X形状，故称之为X舵，其4个方向舵可以独立运行，与传统的交叉舵相比，具有舵效高、机动性强、噪声低、抗沉性强等优点，当前正在服役的德国212A型以及瑞典的“哥特兰”级潜艇均采用的是X形尾舵。随着软硬件的发展，X舵AUV开始逐渐应用于科研和民用领域。

由于水下环境的复杂性及任务的多变性，这便要求X舵AUV具有稳定可靠的控制方法。文献[7]以对角联动的AUV为对象，以PID为主要控制器，实现了对AUV的有效控制，并进行了湖上及海上实验。文献[8]基于AUV模型已知和模型未知情况下设计了改进的滑模控制方法，能够实现控制量的平滑输入，控制效果良好。文献[9]基于滑模控制提出了X舵水下航行器在传感器失效情况下的最优鲁棒轨迹跟踪，并通过仿真实验验证了其有效性。部分研究通过深度挖掘算法及X舵本身的优势，在一定故障范围可实现容错控制，文献[11]基于设计了在双舵、三舵及四舵工作模式下的AUV控制体系，能实现执行器在一定故障范围的容错控制。本文中研究对象为一种可独立运动的X舵水下潜航器，首先建立了X舵AUV控制体系并设计改进的滑模控制器，其次对方向舵舵力分析及控制分配算法设计，最后通过仿真实验验证改进控制器的有效性。

2 X舵水下潜航器运动控制体系及建模

2.1 运动控制体系结构

X舵水下潜航器是典型的过驱动系统，也即是控制量维数大于被控量维数，因此相对与传统的十字舵水下潜航器，其运动控制体系结构相对更加复杂，X舵水下潜航器每个舵的操作都会在6个自由度上引起潜航器整体方向信息的变化，因此在在控制体系结构中还需要考虑控制力在方向舵上分配问题。控制分配是控制指令与执行机构之间的映射，根据系统控制要求和约束条件对方向舵进行合理配置。不仅如此，控制分配还可以发挥系统的过驱动的性能，通过发挥剩余方向舵的性能，从而实现容错控制。X舵水下潜航器运动控制体系结构如图1所示。

图1 X舵AUV运动控制体系结构框图Fig.1 X-ruderAUV motion control system

2.2 X舵水下潜航器建模

为了便于描述X舵AUV在水下六自由度运动，参考SNAMT和ITTC推荐的坐标系于名词术语，本文中设计了2个坐标系，分别位随体坐标系-和大地坐标系-，4个舵位于船尾，且舵轴中心线与AUV中线面之间的夹角为45°，相邻2个舵之间的角度为90°，4个舵形状相同且可独立操控，如图2所示。文献[8]将AUV运动学模型解耦成为一个水平子系统和一个垂直子系统，本文中基于该解耦的运动学模型展开研究，其中水平子系统可以描述为：

图2 X舵AUV结构示意图Fig.2 X-rudder AUV coordinate system definition

(1)

其中

+||||+||||

1=++||||+||||

垂直子系统可以描述为：

(2)

其中

+||||+||||

1=++||||+

||||-sin

式中:代表潜航器质量；、、代表线速度；、、代表角速度；、分别表示横摆力和偏航力矩；、垂荡力和俯仰力矩，其他参数可通过仿真软件直接或者间接测得水动力系数。

针对X舵潜航器的控制问题，潜航器的方向舵以及其控制分配问题的研究也是非常必要的，因此有关方向舵的建模及受力分析在第四节进行详细阐述。

3 X舵水下潜航器控制策略设计

滑模控制作为应用较为普遍的控制策略，具有结构简单，响应速度快，鲁棒性强等优点。本文中基于滑模控制策略本身固有的高频抖振问题，设计一种改进的趋近律来逼近滑模面，利用饱和函数代替符号函数减小其对控制效果带来的不利影响，在此基础上设计趋近律来调节运动点在不同区段到达滑模面的速度，以提升整体控制策略的控制效果。

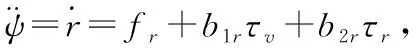
(3)

其中 为期望的航向，设计滑模函数为：

(4)

其中为正常数，对所设计滑模函数求导可得：

设计改进的幂次趋近律为：

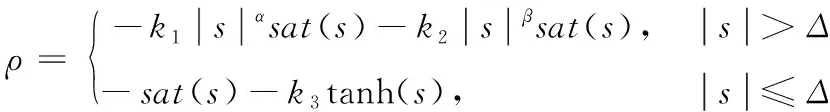
(5)

定义Lyapunov函数为：

则

根据Lyapunov稳定性理论，设计控制律为：

(6)

进一步地，验证所改进滑模控制器的稳定性：

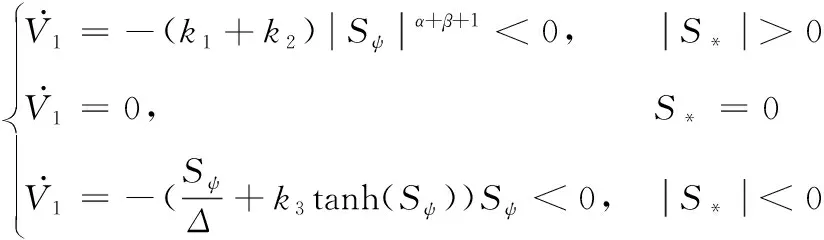
(7)

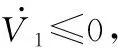
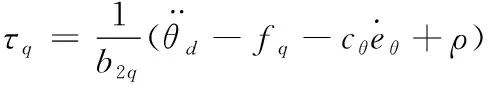
(8)

4 X舵水下潜航器控制分配设计

4.1 X方向舵舵力及控制效率矩阵分析

X舵水下潜航器4个方向舵位于船尾，且舵轴中心线与潜航器中线面之间的夹角为45°，相邻两方向舵之间的角度为90°，4个方向舵形状相同且可以独立操作，其配置形式如图3所示。如果方向舵偏转方向与图中所示方向相同，则表示方向舵偏转角度为正，相反则为反。为了方向舵的舵力分析，假设控制指令与执行机构的输出之间的映射为线性，且不考虑方向舵与潜航器及舵与舵之间的耦合问题。

图3 X方向舵的配置形式示意图Fig.3 The configuration of the X-rudder

因此由文献[10]中舵升力计算公式为：

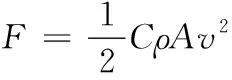
(9)

式中：为升力系数；为流体密度；为舵的受力面积；为水流速度。其中升力系数与方向舵的舵角近似线性关系，因此可以导出方向舵的力矩表达式为：

(10)

为实现舵潜航器俯仰和艏向控制，因此可得相应的横向力矩和垂直向力矩为：

(11)

最终可得舵水下潜航器期望的控制力矩与方向舵输入指令之间的映射关系为：=，也即是：

(12)

其中为舵叶的偏航力矩系数，为舵叶的俯仰力矩系数。

4.2 X舵水下潜航器控制分配

X舵水下潜航器作为一种过驱动控制系统，控制分配技术是必不可少的。控制分配技术即是在考虑执行器约束条件下，以控制分配精度和控制能耗为目标函数，以达到最优的控制分配效果。文献[14]提出一种基于L’evy flight理论的控制分配算法，取得不错的控制分配效果，文献[15]提出一种基于改进的二次规划算法智能控制分配算法，减少了算法迭代时间，提高了控制分配效率。本文中采用文献[8]中的二次规划算法对该问题进行描述：

(13)

算法迭代过程如下：

1选择优化变量和Hessian矩阵的初始状态；

2求解QP子问题，选择迭代点；

3基于更新优化变量和；

4以拉格朗日形式计算目标函数；

5判断是否收敛，如果是，跳转步骤6，否则，重复步骤2～5；

6算法结束。

5 仿真验证

为了验证所设计控制体系的有效性，本文中以X舵水下潜航器为对象，采用文献[14]中的潜航器参数，完成俯仰和航向控制仿真，并与未改进滑模和PID控制器进行对比。其中控制器参数=05，===1,=05,=2，初始俯仰角为0°，目标俯仰角设置为60°，初始航向角为0°，目标航向角设置为-10°；为进一步验证改进滑模控制策略的有效性，对AUV进行定深路径跟踪仿真，初始点设置为(-1 000，-3 000，60)，路径点设置为(3 000，1 000，60)，(2 000，2 000，60)，(-2 000，-2 000，60)，(-3 000，-1 000，60)，(1 000，3 000，60)，方向舵最大舵角设置为30°，最后给出路径跟踪过程中方向舵的控制输入变化曲线。

如图4和图5为X舵潜航器航向和俯仰控制仿真曲线。可以看出，3种控制方法都能使潜航器平稳的接近所需的航向角和俯仰角，并最后达到稳定状态。但相比于未改进的滑模和PID控制方法，改进的滑模控制方法有着更快的收敛速度，表明该方法在航向和俯仰控制方面性能更加突出；控制过程平稳未出现振荡和波动，且超调更小，削弱了系统临近稳态时的高频抖振的不足，验证了前文中对改进滑模控制策略的优势分析。

图4 航向控制仿真曲线Fig.4 Heading control simulation diagram

图5 俯仰控制仿真曲线Fig.5 Pitch control simulation diagram

表1给出了3种控制方法在航向和俯仰控制稳定到达稳态值的调节时间，改进的滑模控制在航向和俯仰控制到达稳态值的时间更短，响应更加快速；表2给出了滑模控制改进前后在航向和俯仰控制的定量，数据表明改进的滑模控制均方误差更小，进一步证明了改进控制方法的优越性。

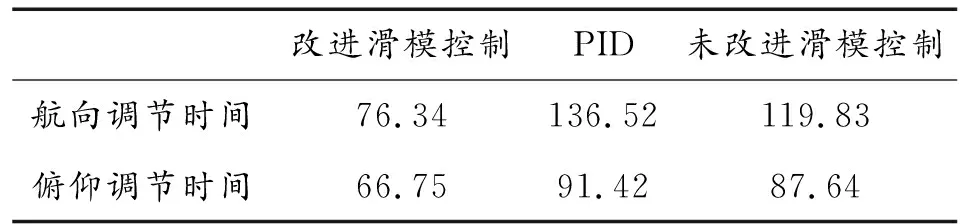
表1 航向和俯仰控制调节时间/sTable 1 Heading and pitch control adjustment time

表2 航向和俯仰控制定量Table 2 Quantitative comparison of heading and pitch control

图6为潜航器定深情况下的期望路径曲线和跟踪路径曲线，结果可以看出，潜航器可以沿着所需的路径移动，每次转弯时都会偏离期望轨迹，但在控制器干预下很快返回路径。图7为路径跟踪过程中方向舵的控制输入曲线，可以看出航向变化过程中舵角最后能以平滑的姿态趋于稳定，有效缓解了滑模控制的抖振问题。

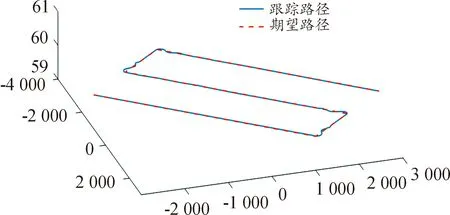
图6 定深情况下的期望路径和跟踪路径仿真曲线Fig.6 Depth-fixed path tracking simulation diagram

图7 路径跟踪过程中方向舵控制输入曲线Fig.6 Rudder control input during path following

6 结论

1) 航向控制仿真中，与未改进滑模控制相比，航向调节时间减少了43.49 s；俯仰控制仿真中，与未改进滑模控制相比，俯仰调节时间减少了20.89 s。

2) 通过定量比较，在航向和俯仰控制过程中，改进的滑模控制策略的均方误差为16.532 3和1.932 5，与未改进滑模控制策略相比更小，表明了改进滑模控制策略优越。

3) 在定深路径跟踪过程中，潜航器在控制器下干预下能够跟踪期望路径，舵角输出平滑且最大舵角未超出30°，表明控制器的有效性且减轻了滑模控制的抖振。