电连接器接触件的性能退化规律与寿命预测

骆燕燕，刘 昙，张兆攀，武雄伟

(1.河北工业大学省部共建电工装备可靠性与智能化国家重点实验室， 天津 300130； 2.国家电网山东省电力公司超高压公司， 济南 250000； 3.国家电网河北电力有限责任公司 邯郸新区供电分公司， 河北 邯郸 056000)

1 引言

电连接器被广泛应用于机载设备、航空数据总线、雷达、导弹及卫星等领域，其可靠性对于这些设备的正常运行是至关重要的。国内外学者研究构建的电连接器寿命预测模型主要包括物理模型和数据驱动模型及其组合模型。

物理模型是以电连接器性能退化机理为基础，抽象出的数学模型。例如：Tamai T通过接触电阻的相关特性构建振动和电流综合应力加速退化可靠性评估模型；钱萍等提出的电连接器特征寿命与温度和振动应力间的广义Eyring模型；万梦茹等由失效分布类型，确定的线簧连接器的Arrhenius-Weibull可靠性统计模型。骆燕燕等依据航空电连接器失效时的应变量临界值建立灰色模型进行寿命预测。

数据驱动模型是依据采集的实验数据进行特征分析与提炼，用数学模型拟合其变化规律。例如，Fu R针对大功率镀银电连接器建立了接触电阻值的变化率与振动频率和微动位移间的微动磨损退化模型；George T.Flower构建了某型号汽车连接器接触电阻值的变化率与频率和加速度间的关系模型。Yi Ren等建立了接触电阻与振动和电流加速应力的关系模型。王世娇等依据不同温度应力下，接触可靠度与接触电阻退化率之间的关系，建立了电连接器贮存可靠性统计模型。

此外，Sun B等基于失效机理和粒子滤波的预测方法，建立电连接器寿命组合预测模型。马洁等建立基于威布尔分布和高斯分布的寿命模型，实现动车组电连接器的寿命预测和可靠度评估；McBride考虑了接触材料性能参数和表面膜的影响，提出了一个低频微动下接触压力和最小接触电阻间的关系模型。

电连接器通过插针与插孔间的可靠接触实现电气连接和信号的传递。插针和插孔属于过盈配合式机械连接，在振动应力作用下极易发生微动磨损现象。大量研究表明，接触件间微动磨损产生的磨屑是电连接器性能退化及失效的主要原因之一。电容层析技术根据被测物质各相具有不同的介电常数，当各相组分分布或浓度分布发生变化时，将引起被检测对象的等价介电常数发生变化，从而使测量电极对间的电容值发生变化，在此基础上，可利用相应的图像重建算法重建被测物场的介电分布图。接触电阻可以作为退化量参数进行寿命预测研究，但是无法为电容层析技术提供便利。通过电容层析采集的电容数据可以实现电容层析成像，与此同时无法预测寿命。因此，本文拟依据电容层析技术进行状态监测，分析采集到数据的变化规律并与接触电阻进行关联，最终预测其微动磨损寿命。

2 电连接器微动磨损试验

本文选用某型号M系列圆形连接器接触件为研究对象进行微动磨损试验，其试验装置原理如图1。

图1 电连接器微动磨损试验装置原理框图Fig.1 Schematic diagram of fretting wear test device for electrical connector

试品以3个不同方向等间隔有序安装在振动台上，如图2所示，其中向振动为振动方向与接触件试品轴向垂直且与插针开槽平行；向振动为振动方向与接触件试品轴向及插针开槽垂直；向振动为振动方向与接触件试品轴向及插针开槽平行。

图2 振动台上试品安装示意图Fig.2 Schematic diagram of sample installation on shaking table

磨屑感应特征值检测单元中电容传感器阵列分为上、下2层，每层8个电极，基于阵列电极的电容边缘效应，本文依次采集相邻电极对(如：1-2、2-3等)间电容值。因此，由插针开槽分割成的2个接触区域A、B又可细分为1-2、2-3和3-4子区域；5-6、6-7和7-8子区域及4-5和8-1子区域，如图3所示。本文作者前期研究证实电极对间电容值的变化可反映出接触件的接触面上不同子区域上磨屑堆积量的变化。

图3 磨屑感应特征值检测单元(a)和电容传感器阵列电极设置接触子区域磨屑堆积分布感测(b)示意图Fig.3 Schematic diagram of chip induction eigenvalue detection unit(a)Capacitor sensor array electrode setting(b)Sensing diagram of debris accumulation and distribution in contact sub-area

微动磨损试验中，试品施加的高频振动激励条件如表1所示，每组试验中分为、、向振动试品，每10万次定时监测磨屑特征参数值即电容值和接触电阻值。将每次监测的电容值与初始电容值的差值作为磨屑感应特征值。

表1 电连接器微动磨损试验方案Table 1 Fretting wear test scheme of electrical connector

3 微动磨损性能退化数据分析

3.1 磨屑特征值总量的变化规律

本文将每个试品16个阵列电极间检测的磨屑感应特征值求和进行分析。部分试品磨屑特征值总量变化柱状图如图4。

由图4可知：

图4 不同高频振动激励下接触件间磨屑感应特征值总量变化柱状图Fig.4 Bar chart of total variation of chip induction characteristic values between contacts under different high-frequency vibration excitation

1) 随着振动次数的增加，试品的磨屑感应特征值总量∑Δ均呈现上升趋势；其变化大致可分为3个阶段：微动初期(0～20万次)，∑Δ小幅快速增长，增幅约0.1 pF；20～40万次期间为缓慢增长期；40～100万次期间，为类线性增长期。100万次时，∑Δ值比20万次时约增加了4～7倍。由此可以推测，微动磨损初期接触件间的接触斑点被剪切成磨屑，起始磨损率较高，此阶段被称为微动磨损的磨合期，即发生摩擦面的相互适应，直至达到所谓的平衡粗糙度。之后，部分磨屑在反复研磨发生细化后，会起到固体润滑剂作用，从而改变接触表面的摩擦因数，磨损量增长减缓，插针插孔处于稳定的摩擦状态，磨损相对低而稳定。随着磨屑的不断增加且被氧化，接触区域压力再分布，区域中心磨粒磨损加重，凹坑加深，使接触面越来越粗糙。插针插孔摩擦表面损伤，其配合间隙发生变化，磨损逐渐加剧。

2) 随着振频及振动加速度的增加，∑Δ呈现上升趋势。如振动加速度为4，100万次时，振频为100 Hz、125 Hz和150 Hz，向振动试品的分别为0.40 pF、0.49 pF和0.58 pF；而向和向振动试品分别为0.39 pF、0.46 pF、0.53 pF和0.39 pF、0.45 pF、0.52 pF。振频100 Hz时，加速度由4增至12，-10#试品的∑Δ(0.54 pF)比X-2#试品(0.39 pF)约增加38.46%。由此推测，振动加速度的增加可能会增大每次微动时的微动位移量，振动频率的增大可能会引起接触件表面温度快速升高，促进表面金属化学反应，从而加速微动腐蚀与磨屑堆积，加剧微动磨损程度。

3)向振动时接触件的磨损比向和向振动略为严重。如在150 Hz、8下振动100万次时，-30#试品的∑Δ为0.58 pF，分别高于-30#试品(0.51 pF)和Y-30#试品(0.52 pF)13.74%和11.54%。由此可推测试品向(沿轴向)振动时，其插针插孔间相对位移更大，产生的磨屑更多，从而导致微动磨损更为严重。

由上述分析可推测，接触件高频微动磨损为磨屑快速堆积的过程，其磨损程度与微动次数、振频和加速度为正相关；不同振动方向下微动磨损程度存在一定的差异。

3.2 接触电阻的变化规律分析

微动磨损过程中，部分试品接触电阻的变化曲线分别如图5—图7。

图5 部分X向振动试品接触电阻的变化曲线Fig.5 Change curve of contact resistance of some X-direction vibration samples

图6 部分Y向振动试品接触电阻的变化曲线Fig.6 Change curve of contact resistance of some Y-direction vibration samples

图7 部分Z向振动试品接触电阻的变化曲线Fig.7 Change curve of contact resistance of some Z-direction vibration samples

由图5—图7可以看出：

试品接触电阻值的变化规律与磨屑感应特征值总量∑Δ相似。

1) 随着振动次数的增加，试品接触电阻值总体呈现上升趋势，但未显现出明显的阶段性变化特征；接触电阻的波动范围约为0.02～0.13，但均未超过电连接器接触件的接触电阻阈值。

2) 振动加速度增加，对接触电阻最大值及其波动量均有影响。如振动100万次时，-34#试品(150 Hz，12)的接触电阻最大值为0.285，比-26#试品(150 Hz，4)的0.230约增加23.91%；波动量分别为0.08和0.04，约增长1倍。

3) 振频的增加对接触电阻值的波动量影响相对较大，呈正相关。如振动频率为100 Hz、125 Hz、150 Hz，向振动试品接触电阻最大波动量分别为0.05、0.06和0.08。

4)向振动试品的接触电阻最大值和波动量均比向和向高。如-18#试品(125 Hz，8)、-18#试品(125 Hz，8)和-18#试品(125 Hz，8)的接触电阻最大值分别为0.24、0.24和0.28。向振动试品接触电阻波动量范围是0.05～0.13，约为、向(0.02～0.08)的1.6～2.5倍。

3.3 磨屑特征值总量与接触电阻值的关联性分析

研究表明，磨屑是造成电连接器微动磨损性能退化及失效的根本原因，为此，本文对磨屑感应特征值总量∑Δ与接触电阻值之间的关联性进行分析。与∑Δ的相关系数计算公式，如式(1)所示。

(1)

式中，(,)为接触电阻和磨屑感应特征值总量∑Δ的相关系数；(,)为和∑Δ的协方差；[]为的方差；[]为∑Δ的方差。部分试品的与∑Δ的相关系数如表2所示。

表2 部分试品接触电阻与磨屑感应特征值总量的相关系数Table 2 The correlation coefficient between the contact resistance of some samples and the total amount of abrasive chip induction characteristic value

从表3可以看出，试品接触电阻与磨屑感应特征值总量整体上呈现正相关性。3个振动方向下的34#试品(150 Hz，12)与∑Δ的相关系数均超过0.9，接触电阻和磨屑感应特征值在高振频高振动加速度下呈现出极高的相关性。由此可见，磨屑感应特征值总量可一定程度反映电连接器接触件磨损程度和接触性能的退化进程。

表3 相关系数与相关性Table 3 Correlation coefficient and correlation comparison table

4 微动磨损寿命预测

4.1 微动磨损性能退化模型的构建

电连接器的微动磨损是一个磨屑不断堆积，引发性能非单调性退化的过程，其满足Wiener过程的要求。Wiener过程的定义为：① 退化量的初值(0)=0；② 退化过程{()，≥0}具有平稳独立增量性；③ 对于每个>0，()服从正态分布(0,)。

本文选取磨屑特征值总量作为电连接器接触件的退化特征量。根据中心极限定理对磨屑特征值总量每振动10万次的退化量进行分段累积，构造出每段磨屑特征值总量的累积退化量，则有：

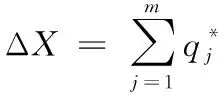
(2)

对磨屑特征值总量的累积退化量(以-33#试品为例)进行正态分布检验的结果如图8所示。

由图8可见，数据点基本在一条直线上，由此可认为磨屑特征值总量累积退化量服从正态分布，因此电连接器的接触性能退化过程符合Wiener过程。令=，=，电连接器接触性能退化模型可构建为：

图8 X-33#试品电连接器磨屑特征值总量累积退化量的正态分布检验曲线Fig.8 Test curve of normal distribution of total cumulative degradation of wear chip eigenvalue of electrical connector X-33#

()=+()

(3)

本文将电连接器磨屑特征值总量累积退化量分为n=10个阶段，利用极大似然估计法分别求得各个阶段磨屑特征值总量对应的漂移参数μ、扩散参数σ和失效阈值L，即：

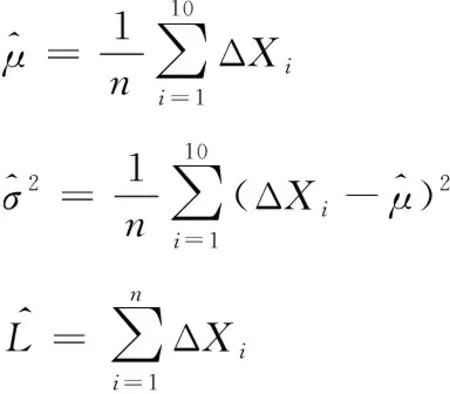
(4)

将式(4)中估计的μ和σ代入式(3)，可构建出电连接器的接触性能退化模型。

4.2 电连接器寿命预测

如图9所示，当电连接器的退化特征量第一次达到失效阈值时，即认为其寿命的结束。

图9 剩余寿命预测曲线Fig.9 Residual life prediction curve

因此，电连接器寿命可定义为：

=inf{:()≥|(0)≤}

(5)

对当前时刻，电连接器的剩余寿命可定义为：

=inf{∶(+)≥}

(6)

将逆高斯分布与Wiener模型非单调退化过程结合，可得电连接器的剩余寿命概率密度函数为：

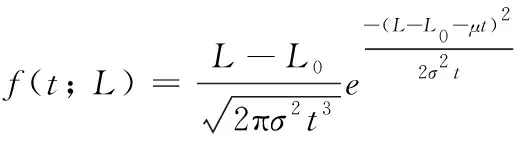
(7)

式中：为电连接器运行到时刻的磨屑特征值总量实际累积退化量。

电连接器剩余寿命的期望和方差为：

(8)

在失效阈值下，电连接器运行到时刻的分布函数为：

(9)

由式(9)推算，电连接器运行到时刻的剩余寿命可靠度函数为：

(10)

其中，为标准正态分布函数。

4.3 预测结果分析

表4所示为微动磨损性能退化模型中漂移参数和扩散参数的估计值。

表4 微动磨损性能退化模型的参数Table 4 Parameter estimation of fretting wear degradation model

(11)

由图10可靠度曲线可以看出，当振动次数约130万次时，电连接器的可靠度开始显著降低。

图10 电连接器磨屑特征值总量可靠度曲线Fig.10 Total reliability curve of electrical connector chip eigenvalue

图11 电连接器剩余寿命概率密度函数曲线Fig.11 Probability density function curve of remaining life of electrical connector

一般情况下，电连接器剩余寿命的期望值可作为预测值，即：

(12)

由表5可以看出，在高频高加速度下，利用磨屑特征值总量作为退化性能参数可以实现电连接器接触件的寿命预测。由此可以在电容层析检测磨屑分布的同时，为寿命预测提供可靠的数据支持，为后续试验提供了便利。

表5 部分试品剩余寿命预测值及误差Table 5 Predicted value and error range of residual life of some samples

5 结论

1) 微动次数增加，磨屑特征值总量与接触电阻的变化规律类似，电连接器的微动磨损可分为磨损初期、磨损稳定期和严重磨损期；而接触电阻值呈现“低且稳定”、“渐增”和“剧增和剧烈波动”。

2) 电连接器高频微动磨损程度与微动次数、振动频率和振动加速度为正相关；不同振动方向下，微动磨损进程存在一定差异，轴向振动时磨损最严重，磨屑堆积量约比其他振动方向增加12%。

3) 高频高振动加速度下，磨屑特征值总量和接触电阻值呈现极高的相关性。将磨屑特征值总量作为退化量，通过Wiener退化过程，构建电连接器微动磨损性能退化模型，可预测剩余寿命，通过试验证实了准确性。