基于SFPN的轨道交通车门故障诊断方法研究
覃 语,徐永能
(南京理工大学 自动化学院, 南京 210094)
1 引言
轨道交通作为现代化社会中最重要的交通工具之一,在缓解交通堵塞和促进城市发展方面扮演着重要角色。随着时代的发展,城市轨道交通的客运压力不断增大,车门系统作为轨道车辆中结构最复杂、涉及零部件最多的系统,其故障频率也随着使用率的升高而不断增大,严重影响了列车运行的安全性和可靠性。因此,需要一种准确、适用性高的车门系统故障诊断方法,以快速确定故障部件,提高检修效率,进而保障地铁高效安全运行。
对于车门故障诊断的相关研究,常用到的理论方法包括人工神经网络、专家系统、贝叶斯网络、Petri网理论等。其中,Petri网模型法具有数学逻辑严谨、物理意义明确、逻辑推理清晰等优点,适用于复杂的车门故障分析。该方法不仅可以快速判断发生的故障类型,还可以追溯故障发生线路,快速定位到故障发生点。Yaung等基于传统Petri网理论引入了FPR权重的概念。在此基础上,针对多因果式网络结构,Ha等在权重FPR模型中引入输入权重、输出权重,提出了FPN模型。Liu等针对已有FPN模型提出了动态自适应模糊Petri网。该并行推理算法基于极大代数,可以结合专家系统动态完成逻辑推理。
传统模糊Petri网模型(TFPN)对于故障现象仅用隶属度一个参数来描述。但根据以往的工作经验得知,故障事件的发生还常伴随着不确定性,TFPN模型法却无法对此进行量化。本文中分析了现有车门故障模式及其影响,提出了一种基于球型模糊Petri网的地铁车门系统故障诊断模型。该模型能够更全面地评估故障事件发生的可能性,给出更可靠的故障传播路径推理结果,从而有效提升车门系统的安全性和可靠性。
2 车门故障分析
2.1 工作原理
车门系统结构复杂,车门的开启、关闭动作主要由电气控制模块、车门控制单元EDCU模块及机械动作模块3个模块来实现。电气控制模块与机械动作模块之间通过电子门控制器EDCU连接。电气控制模块负责将控制台发出的开门信号、零速信号、驱动电机运转信号等信息传递给电子门控制器EDCU。EDCU与电机之间产生交互信息,传递车门运动速度信号至机械运动模块。三者关联交互工作,共同控制车门系统的开关动作。车门系统结构原理如图1所示。
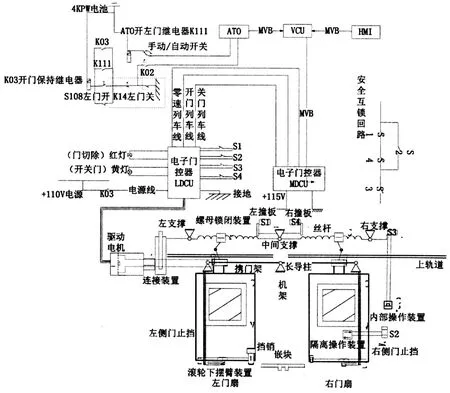
图1 车门系统结构原理示意图Fig.1 Door system structure
当需要开启车门时,车辆控制中心会向车门系统发送零速信号。列车如果处于自动驾驶模式(ATO)时将会自动将零速信号、开门信号传至EDCU。EDCU进而输出电信号驱动电机,通过电机带动机械动作模块来完成开门动作。当需要关闭车门时,EDCU同样会将从车辆控制中心收到的关门信号转为驱动电机运作的电信号。车门关好后,锁闭行程开关S1闭合,EDCU接收到车门关闭信号后传递给制动单元,制动单元对车门进行制动反馈,车门的止挡、嵌块、挡销等部件将会配合完成对车门的锁紧固定。工作流程如图2所示。
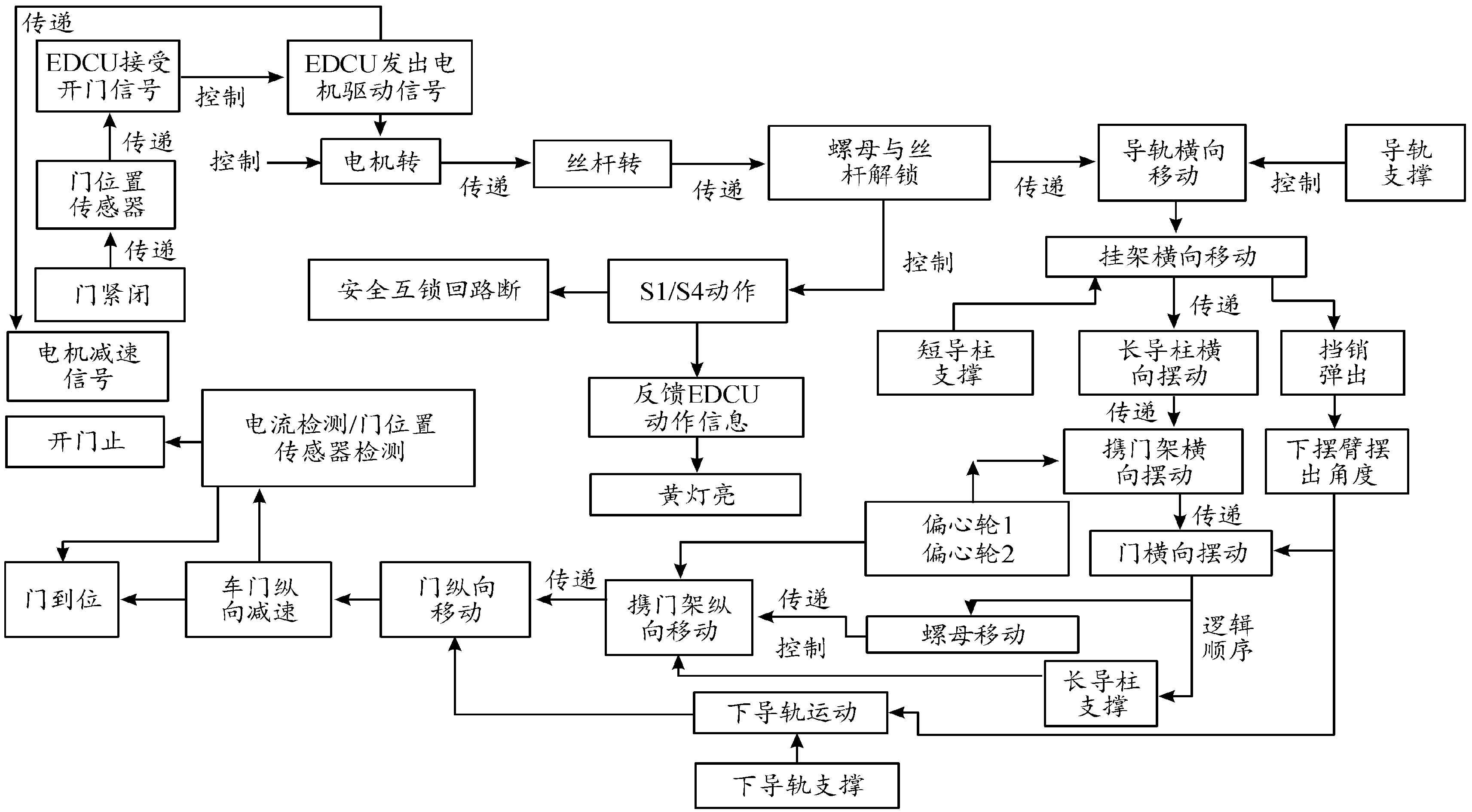
图2 车门系统工作流程Fig.2 Door system workflow
2.2 故障模式分析
根据轨道交通车辆运行经验,总结了6种典型车门故障模式:车门自动开关门故障、车门开门故障、车门关门故障、车门指示灯故障、开关门动作异响、车门操作装置故障。根据表1中故障树相关符号规则,建立车门系统故障模式故障树示意图。
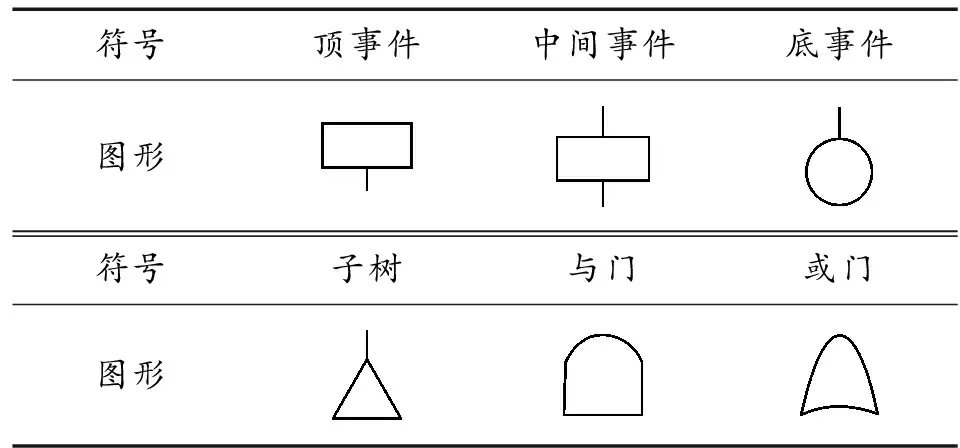
表1 故障树事件符号和逻辑门符号Table 1 Fault event symbol and logic gate symbol
建立车门系统故障模式故障树示意图,如图3—图10所示。

图3 顶事件故障树Fig.3 Top event fault tree
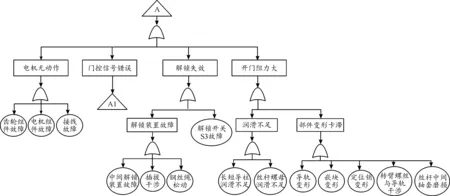
图4 车门开门故障树Fig.4 Door opening fault tree

图5 车门开门故障树子树Fig.5 Door opening fault tree subtree
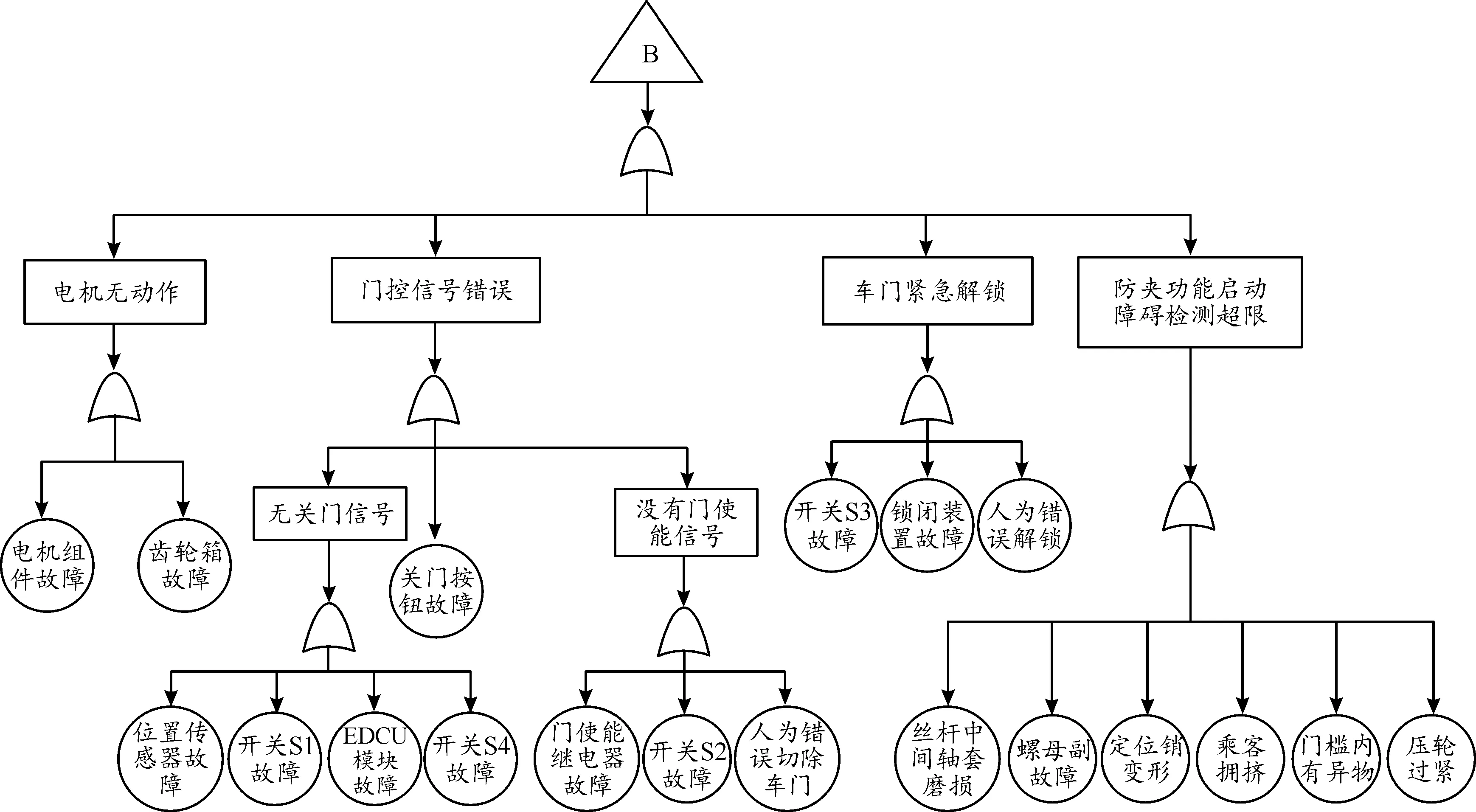
图6 车门关门故障树Fig.6 Door closing fault tree

图7 车门自动开关门故障树Fig.7 Automatic door opening and closing fault tree
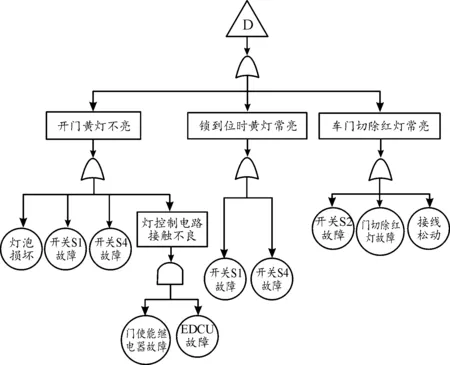
图8 车门指示灯故障树Fig.8 Door indicator fault tree

图9 开关门动作异响故障树Fig.9 Fault tree of abnormal sound caused by door opening and closing
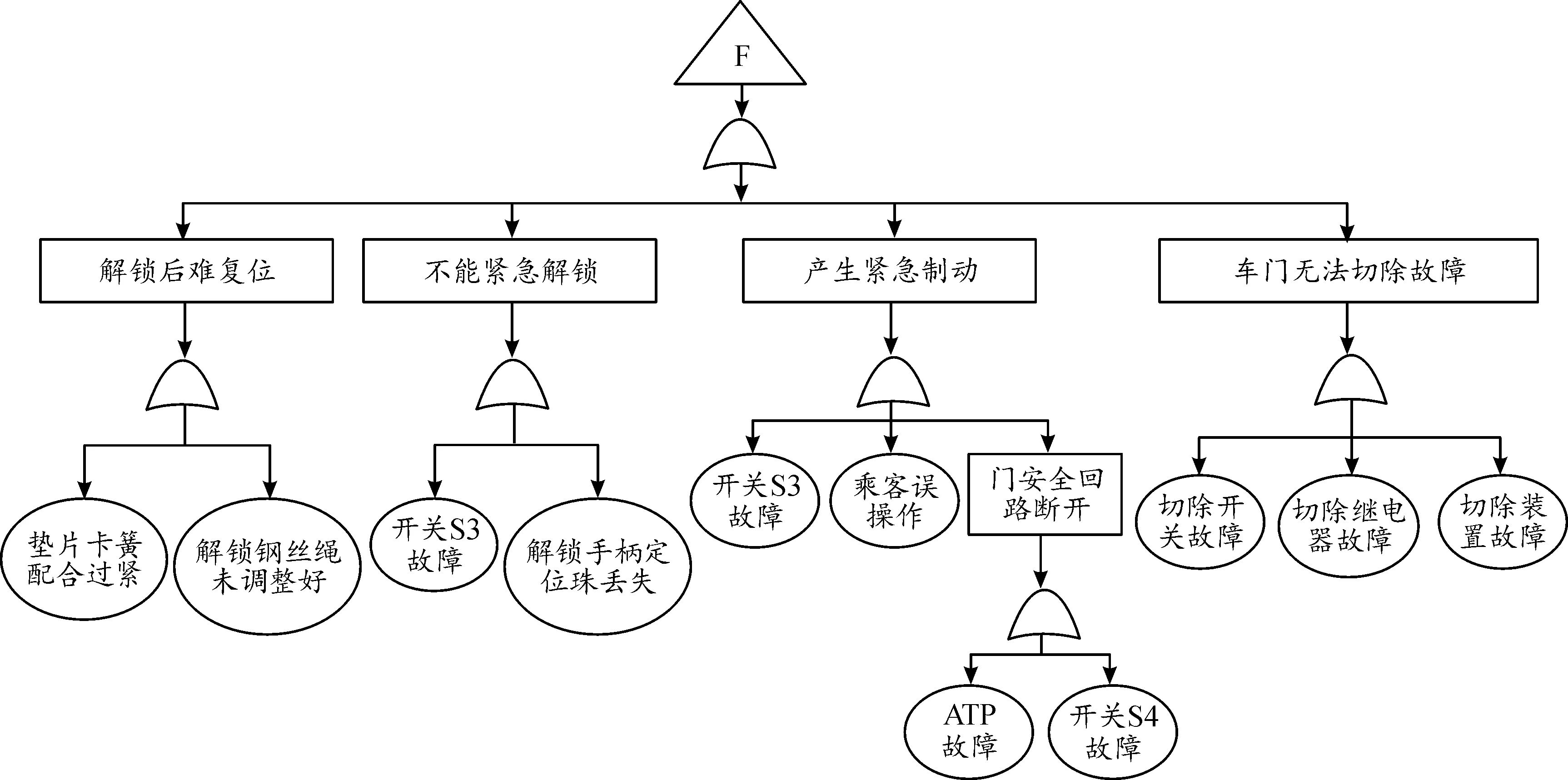
图10 车门操作装置故障树Fig.10 Fault tree of door operating device
3 车门故障诊断方法
3.1 球型模糊Petri网模型
Petri网是20世纪60年代由卡尔·A·佩特里发明的一种用于描述异步、高并发复杂系统的网状结构信息流模型。它既有严格的数学表达式,也有清晰明确的图形表达方法。为了更好地实现Petri网对现实世界系统的描述,Chen等基于事件的不确定性提出了模糊Petri网的概念。
球型模糊Petri网理论基于“球型模糊集”的概念,引入了“中立度”的概念。根据过往的故障维修及记录经验,中立度可以更好地描述专家及检修人员对故障模式的犹豫性。球型模糊Petri网可以定义为一个11元组:

(1)

模糊Petri网中库所与变迁的交互关系如图11所示。“○”表示库所,“|”表示变迁,“●”表示Token,如果一个库所中含有一个Token,则证明此库所代表的状态正在发生。变迁与库所之间通过箭头“→”连接,表示变迁及其触发阈值的信度值。

图11 模糊Petri网模型Fig.11 Fuzzy Petri net model
车门系统故障与Petri网模型的结构映射关系如表2所示。

表2 车门系统故障与模糊Petri网模型映射关系Table 2 Mapping relationship between vehicle door failure and fuzzy Petri net model
3.2 建立车门故障Petri网模型
根据文献[13],车门典型故障模式包括车门开/关门故障、车门自动开关门故障、指示灯故障、开关门动作异响。根据图3~图10的故障树图示可以确定基本故障事件和上层故障模式类型及从属关系,如表3所示。

表3 故障事件与状态表Table 3 Event and status

续表(表3)

续表(表3)
根据表3的信息即可得出故障演变发生的路径及逻辑关系,进而可得到如图4所示的Petri网模型图。由于整体Petri网模型图过于复杂,仅展示“车门开门故障”、“车门关门故障” 的Petri网模型图为例。
图12中的结构关系均为“或”关系,未体现和事件中“与”关系逻辑状态。如“灯控制电路接触不良”的上一状态为 “+”,如图13所示。

图12 p84、p85车门故障模式球型Petri网模型示意图Fig.12 The spherical Petri net model diagram of the door failure mode of events 84 and 85
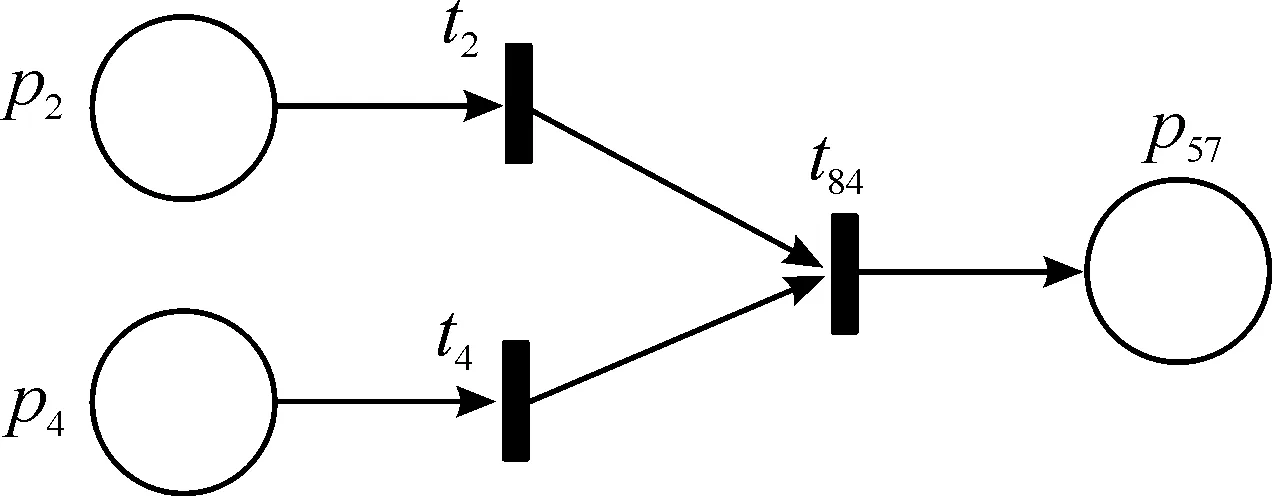
图13 Petri网模型“与”关系示意图Fig.13 Representation of “AND” relation in Petri net model
3.3 SFPN模型计算方法
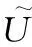
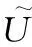
对于日常监测的设备,隶属度不变,按照“中立度:非隶属度:不确定度”的比例进行模糊数据转化,有关规则如表4所示。

表4 模糊转化规则Table 4 Fuzzy transformation rule
对于不定期检修的设备,根据其易发性评级标准进行球型模糊数取值,如表5所示。

表5 部分设备易发性及其模糊数取值Table 5 Part of equipment’s susceptibility and its fuzzy number value

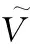



表6 变迁阈值判别规则Table 6 Criterion of transition threshold
4) 库所与变迁见有向弧权重(、)
、为库所输入变迁的权重,为变迁输出库所的权重。假设各有向弧权重相等,且权重总和为1。
5) 模型计算
① 计算初始库所状态:根据式(2)判断变迁是否会发生,得到库所状态矩阵
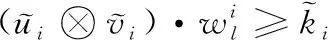
(2)

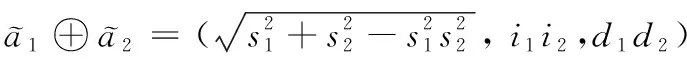
(3)
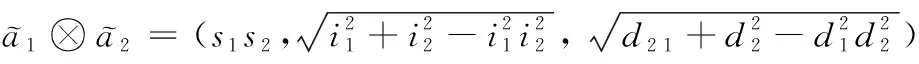
(4)
② 基于输入矩阵计算输入库所信度值
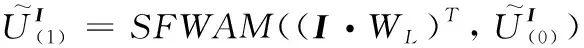
(5)
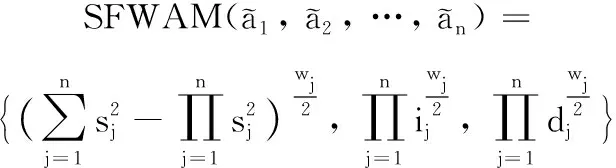
(6)
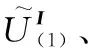
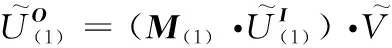
(7)
④ 更新所有库所信度值

(8)
不断迭代计算,直至库所信度值不再变化,即得到所有故障事件的最终信度值。
4 SFPN车门故障诊断模型优化验证
4.1 初始库所、变迁及变迁阈值信度值计算
由于篇幅限制,仅以车门开门故障模式为例进行模型求解。
1) 初始库所信度值
根据3.3节及表4、表5给出的计算规则,得到各库所初始信度值如表7所示。
表7中~并非基础故障事件,因此初始信度值为0,中立度为0,非隶属度为1。
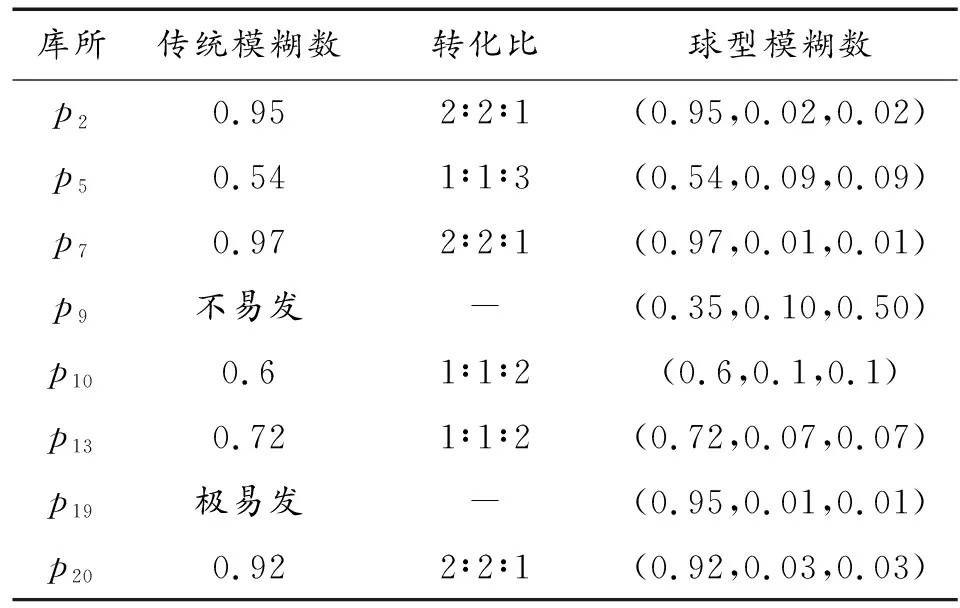
表7 车门开门故障库所初始信度值Table 7 Initial reliability value of door opening failure database

续表(表7)
2) 变迁信度值
变迁模糊数的转化同样遵循表4的转化规则,球形模糊数取值如表8所示。

表8 变迁、变迁阈值Table 8 Transition threshold value table
3) 变迁阈值信度值
根据故障模式危害分类,得到了各故障模式的严重度评级及其球型模糊数取值,如表9所示。

表9 变迁阈值Table 9 Transition threshold value table
4.2 模型求解
车门开门故障Petri网模型中,有23个库所,22个变迁,由此可以得到输入矩阵、输出矩阵如下:

其中,

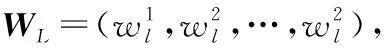
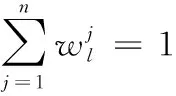
(9)

(10)
根据式(2)计算库所最初始状态
=(1,1,1,1,1,1,1,1,0,1,0,1,1,1,0,0,0,0,0,0,0,0,0)
库所含有一个Token,即故障模式发生,状态为“1”,反之则为“0”,根据式(5)(6)计算输入库所信度值:
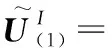
[(093,010,010),(029,013,013),
(086,004,004),(017,014,051),
(042,013,013),(065,008,008),
(086,004,004),(087,004,004),
(019,013,013),(087,004,004),
(015,015,015),(087,004,004),
(042,013,013),(086,004,004),
(0,0,1),(0,0,1),(0,0,1),(0,0,1),
(0,0,1),(0,0,1),(0,0,1),(0,0,1),(0,0,1)]
计算输出库所信度值
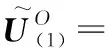
[(09,00,006),(00,00,10),
(042,01,017),(08,00,009),
(07,00,014),(039,001,018),
(084,00,007),(085,00,009),
(082,00,008),(00,00,10),
(081,00,008),(042,00,017),
(09,00,006),(031,00,016),
(00,00,10),(00,00,10),
(00,00,10),(00,00,10),
(00,00,10),(00,00,10),
(00,00,10),(00,00,10)]
根据式(1)~式(8)的方法计算出最终信度值,将其与TFPN模型结果一起列表,如表10所示。
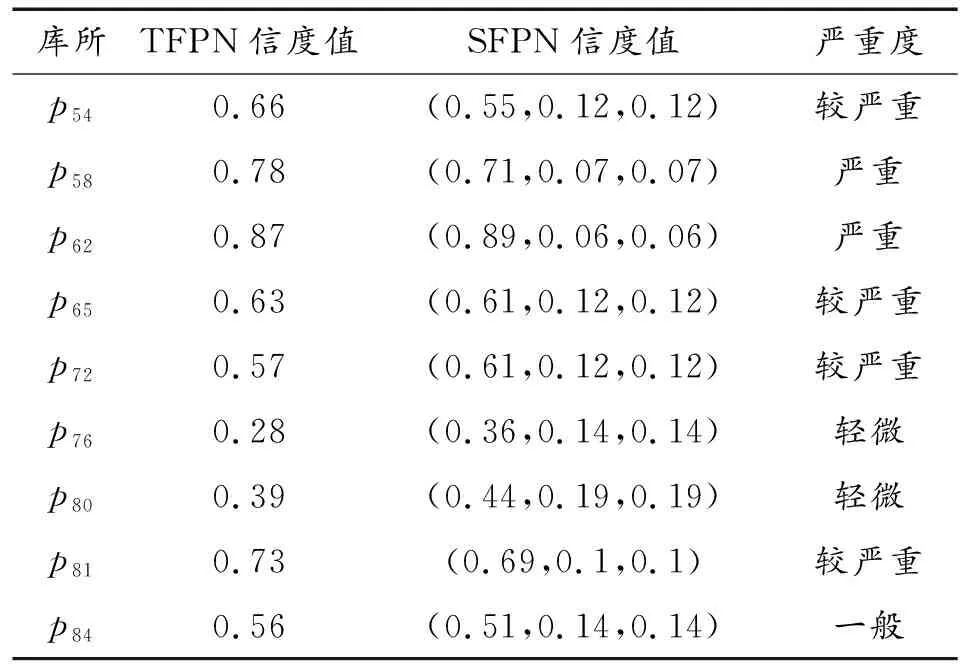
表10 模型故障模式信度值推理结果Table 10 Comparison of inference results of reliability values of failure modes
将TFPN模型与SFPN模型信度值作图,如图14所示。由图可知,两者信度值趋势大致相同,证明SFPN模型法具有可靠性。

图14 2种模型信度值曲线Fig.14 Comparison of reliability values between two models
根据文献[16]中对球型模糊元中对球型模糊集的比较方法,可结合球型模糊值中的中立度、非隶属度数值对故障事件信度值严重程度进行进一步判断。
根据式(11)计算故障事件信度值的得分函数,再根据式(12)进行2个故障事件严重度的判断。

(11)
式(11)中,[0,q]为信度值取值范围,故此处取q=1。s、d为球型信度值中的隶属度、非隶属度。
()>(), 则>
()<(), 则<
(12)
当S(T)=S(T)时,需要根据式(13)进一步计算精度函数,并根据式(14)进行严重度判断。
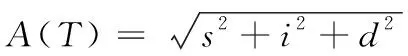
(13)
式(13)中,s、i、d为隶属度、中立度、非隶属度。
()=()且()>(),则>;
()=()且()<(),则<;
()=()且()=(),则=;
(14)
以解锁失效导致的车门开门故障为例,推演其故障传播路径,如表11所示。
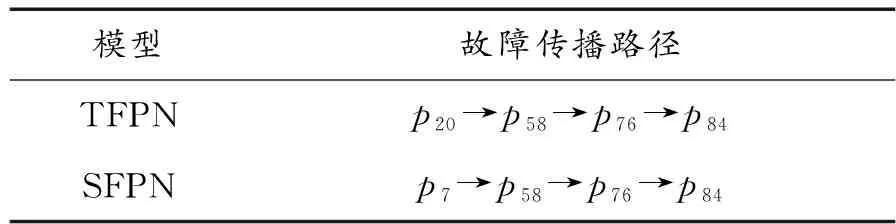
表11 故障传播路径Table 11 Comparison of fault propagation paths
TFPN模型中推理的故障传播路径源头为“解锁撞块断裂”,如表7所示,初始模糊信度值为(0.92,0.03,0.03);SFPN模型给出的传播路径源头为“插拔干涉”,初始模糊信度值为(0.97,0.01,0.01)。
根据球型信度值中的隶属度,隶属度为097,隶属度为092,初步判断严重程度>。
根据式(11)计算得到和的得分函数分别为139和136,因此进一步判断严重程度>。由于二者得分函数不同,不需要进一步计算精度函数。
因此可以判断:最可能因解锁装置故障而导致车门开门故障的传播路径应为→→→。
由此可以得出结论,结合SFPN模型法中补充的中立度、非隶属度2个判断标准,该方法能比传统模型法更全面、准确描述故障模式。
5 结论
所使用的基于球型模糊Petri网模型(SFPN)的车门故障诊断方法,在保证可靠性的同时,提升了准确性。SFPN模型法可以给出更准确的故障传播路径,适用于复杂地铁的故障诊断。故障发生时,检修人员可以根据该模型给出的推理路径进行逆向检索,快速确定故障发生源,有效提升检修工作效率。

