不同维分数阶混沌预设时间有限时间投影同步
邵克勇 蒋卢杰 王婷婷

摘 要:對于不同维分数阶混沌系统的投影同步问题,设计了一种自适应滑模控制器。这使得带有内部不确定量和外部扰动的驱动,响应系统能够在任意预设的时间完成同步,自适应律可以逼近未知量的上界。 并针对自适应滑模控制器由于干扰产生抖振的问题,提出了两种解决方案。首先是设计二维滑模控制表,将模糊控制方法加入滑模控制器组成模糊自适应滑模控制器。其次是使用“SuperTwisting”控制律,将滑模控制改进为二阶滑模控制。最后通过数值仿真,可以看到两种解决方案都有效地削减了控制器的抖振现象,证明了方法有效性和正确性,提高了用于实际生产的可行性。
关键词:模糊自适应滑模控制;二阶滑模控制;有限时间同步;分数阶混沌系统;SuperTwisting算法
中图分类号:TP 273 文献标识码:A
Finitetime Projection Synchronization of Different
Dimensionality Fractional Chaos at the Preset Time
SHAO Keyong, JIANG Lujie, WANG Tingting
(School of Electrical Engineering & Information, Northeast petroleum University, Daqing ,Helongjiang 163318, China)
Abstract:For the projective synchronization of fractionalorder chaotic systems with different dimensions, an adaptive sliding mode controller is designed. The drive and response system with internal uncertainty and external disturbance can be synchronized at any preset time, and the adaptive law can approach the upper bound of the unknown. Two solutions are proposed for the chattering problem of adaptive sliding mode controller due to interference. The first is to design a twodimensional sliding mode control table, and add the fuzzy control method to the sliding mode controller to form a fuzzy adaptive sliding mode controller. The second is to use the "SuperTwisting" control law to improve sliding mode control to secondorder sliding mode control.Finally, through numerical simulation, it can be seen that the two solutions have effectively reduced the chattering phenomenon of the controller, proved the effectiveness and correctness of the method, and improved the feasibility of being used in actual production.
Key words:fuzzy adaptive sliding mode control; secondorder sliding mode control;finite time synchronization; fractionalorder chaotic system; SuperTwisting algorithm
混沌现象是对于初值十分敏感的复杂非线性现象,经常出现于自然或人工的系统中。分数阶混沌由于拥有分数阶运算和高度的非线性,呈现出比整数阶混沌更复杂的行为。这个特性对于工程应用十分重要,如降低安全通信中被攻击的风险[1]。近些年,对于分数阶混沌同步的研究受到了广泛关注,关于分数阶混沌系统间的各种同步方式及方法被提出[2-8],但基于不同维分数阶混沌系统的有限时间投影同步的研究还相对较少。结合以上的考虑,本文设计分数阶自适应滑模投影同步的控制方法,在保证了系统鲁棒性稳定的前提下,还能对未知可变的内外因素进行适应,使得系统间的同步时间仅仅依赖于初始条件及参数,无须考虑未知量的上界。
1 预备知识
引理4[12] 如果一个受控系统有如下形式:
式中x∈R是状态变量,φt是干扰量,ut为“SuperTwisting”控制律
其中u1(t)=-λ|x|12sgn(x),2=-αsgn (x),α>0,λ>0为参数,sgn (x)为符号函数。若|t|≤δ,t≥0,δ为已知常数,设定参数
则系统可以在有限时间收敛到原点。
2 不同维分数阶系统预设时间的有限时间投影同步
2.1 问题描述
考虑不同维的分数阶驱动系统与响应系统,它们的形式分别如下:
其中α∈0,1是分數阶微分的阶次,Dα既可以是Caputo型也开始是RL型微分,Y=y1,…,ym∈Rm和X=x1,…,xn∈Rn分别为响应系统与驱动系统的状态变量,gi:Rn→R,i=1,2,…,n是X的非线性函数,Δg(X,t)=[Δg1(X,t),…,Δgn(X,t)]和dg(t)=[dg1(t),…,dgn(t)]分别是驱动系统的内部不确定量和外部扰动,fi:Rn→R是Y非线性函数, Δf(Y,t)=[Δf1(Y,t),…,Δfm(Y,t)]和df(t)=[df1(t),…,dfm(t)]分别是响应系统的内部不确定量和外部扰动。最后u(X,Y,t)=[u1(X,Y,t),…,um(X,Y,t)]为控制信号。假设外部干扰和内部不确定性是有界可微的。
系统间的误差表达式可以写作Ε(t)=Y(t)-A·X(t),Ε(t)=[e1,…,em]∈Rm,其中A=[a1,…,ai,…,am]∈Rm×n为两个系统间投影同步的系数矩阵,ai为行向量。将式(1)和式(2)代入误差公式,系统间误差的分数阶微分方程可以表示为:
2.2 控制器设计
采用以下滑模面:
其中hit被称作终端函数,假设在控制器的作用下驱动系统和响应系统在时间t=T时达到同步,T为预先设置的时间参数。则终端函数hit应当满足在时刻T时hi(T)=0,而在初始条件下hi(0)=ei0。于是选择如下形式终端函数hit:
定理1 对于驱动系统(1)和响应系统(2),在其内部不确定量与外部扰动是未知的情况下,设计公(7)形式的自适应控制器,实现两个系统在时刻T的同步。
证明:将终端函数hit式(5)代入滑模面的表达式(4)中,可以得出t=0时,si(0)=ei(0)-ei(0)=0,即系统一开始便位于滑模面上。滑模面的特性使得误差ei(t),=hit误差函数的轨迹将会按照终端函数的轨迹运行,而在时间t=T时,ei(T)=hiT=0系统达到同步。可以看到系统同步的时间取决于终端函数中参数T的选择。这种终端滑模面的设计方法省略了到达阶段,增强了系统的鲁棒性和精确性。但当出现内部不确定与外部扰动时,系统会偏离滑模面,为了保证系统能在这种条件下返回滑模面,需要对其收敛性进行分析。
当系统的内部不确定与外部扰动上界已知时,设计的lyapunov函数为:
而对于未知的上界,需要引入自适应律,因此将式(8) 改进为
其中i=i=θi,式(9)只有在零点时为0,而其他情况下大于0。由此可以得出该lyapunov函数为正定,对式(9)求导可得
进一步地将式(4)代入式(10)展开,根据引理1可得
根据引理2,在展开后的式子中,分数阶积分算子和分数阶微分算子进行运算可得:
由于扰动都是有界且可导的,根据Hlder空间特性[13]可知,Fui,Gui,DMi,DSi满足之前提出的不等式,因此:
其中kmin =min (k1,k2,…,km),当si=0时t,i=0,导函数为负定。上述不等式证明了误差系统渐近稳定于滑模面,即相轨迹因为扰动离开滑模面时,能够在控制器的作用下回到稳定状态。通过引理3式(13)可以变为
根据有限时间稳定性判据[14],由以上微分不等式可以推导出系统会在有限时间内返回滑模面,其时间上的界取决于参数kmin 。
系统回到滑模面上后,s(t)=0,根据式(4),系统误差与终端函数的关系变为0=ei(t)-hit,误差将会在时间t=T时变为0,从而达到同步。由此可知,只要设计合适的趋近律参数,使得系统返回滑模面的时间远小于同步时间T,那么系统就能在发生微小偏移时迅速回归滑模面,实现在预设时间T达到同步,证明完毕。
2.3 控制器的改进
传统滑模控制的一个缺点便是当滑模面上出现干扰时,控制器会出现剧烈的抖振,这在实际使用滑模控制器的过程中带来了巨大的挑战,抖振不但会给设备带来损害,还会影响系统的表现。模糊控制是基于专家经验所指定的语言规则的集合,运用这些规则集合可以提供适当的模糊控制律,将模糊控制运用到滑模控制,就是所谓的模糊滑模控制[10]。
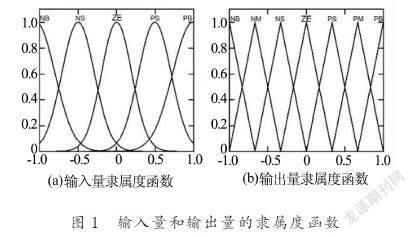
加入模糊控制后,原本控制器中的(ui+|ai·u|+|ai·M|+Si)·sgn si变为(ui+|ai·u|+|ai·M|+Si)·sfi,sfi是经过模糊推理后得出的输出量。模糊控制表可以由专家经验或实验得出,为了使得控制器的输出更加适当,调模糊控制选择两个输入量,这样可以从输入量中获得更多的信息从而防止控制器输出过大出现超调,进而减小或消除控制器中的抖振,选择的两个输入量是滑模面与滑模面的导数。图1为输入量与输出量的隶属度函数。输入量根据数据统计的直方图与呈现出的正态分布曲线选择了高斯函数。输出量需要精确数值,因此选择了三角形函数。
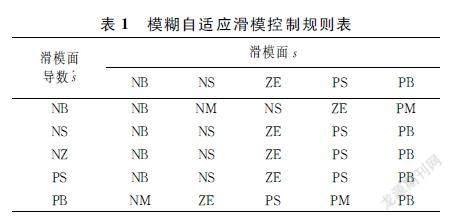
将输出量划分为七个范围,分别是负大(negative big,NB)、负中(negative middle,NM)、负小(negative small,NS)、零(zero,ZE)、正小(positive small)、正中(positive middle,PM)、正大(positive big,PB),而两个输入量被划分为五个范围, 分别是NB、NS、ZE、PS、PB。 表1为模糊自适应滑模控制规则表。
模糊控制的引入虽然可以减小抖振的影响,但作为额外的结构,给控制器的设计增添了复杂度。接下来结合二阶滑模理论中的SuperTwisting算法,对控制器進行改进。
定理 2 对于驱动系统(1)和驱动系统(2),其内部不确定量与外部扰动是未知的,Dα 选为Caputo型,设计如下的自适应控制器,实现两个系统在时刻T的同步
证明:与定理1采用相同的终端函数,系统在初始时间便位于滑模面上,因此为了保证系统能在预设时间达到同步,需要系统在偏离滑模面后在有限时间内返回。将控制器(15)带入滑模面动态系统公式(4)展开并求导,可以得到
根据2.2节中对内部不确定和外部扰动的假设,将Δfi(Y,t)-ai·Δg(X,t)+dfi(t)-ai·dg(t)记为φ(X,Y,t),则|(X,Y,t)|≤δ,δ属于已知常数,所以可得
根据引理4,受控系统si在有限时间内达到稳定点,此时系统达到滑模面,即s(t)=0。系统到达滑模面后,系统的误差就会跟随终端函数hit的轨迹,在时间t=T时达到同步。而趋近律保证了系统偏离滑模面时能够在有限时间内回到滑模面。由此可知,保证在预设时间达到同步的前提是返回滑模面的时间足够短,而返回时间的长短可以由参数来设定,证明完毕。
针对分数阶混沌系统的投影同步问题,通过带有分数阶积分项形式的滑模控制器,将整数阶领域的二阶滑模控制方法应用于分数阶系统上,对整数阶二阶滑模控制的应用进行了扩展。
3 数值仿真
选择拥有内部未知量与外部扰动的四维分数阶超混沌系统和三维分数阶chen混沌系统作为驱动系统和响应系统。首先使用自适应滑模控制器,设置同步时间T 分别为0.5和1,各个维度的误差相轨迹如图2所示,系统的在设定的时间点误差收敛到零达到了同步,证明了控制器的有效性。
图3为时间参数T=1时自适应滑模控制器的输出,可以看出有明显的抖振,为了解决这个问题,紧接着分别采用了模糊自适应滑模控制器与二阶滑模控制器,对驱动和响应系统进行同步实验,时间设置为T=1,图4为使用两种改进后的控制器的误差相轨迹图,可以看到在规定时间达到同步。
图5和图6显示了控制器u1的输出,可以看到在保证了在有限时间同步的同时,运用模糊控制与SuperTwisting控制律的滑模控制器输出曲线光滑连续,使得滑模控制器有效地消除了因为外界扰动带来的抖振。表2在中展现了三种控制器的各项性能,可以看到与自适应滑模控制器相比,模糊自适应滑模控制器在平均收敛时间、最大输出和平均输出三项上的表现更优,而稳态最大误差的表现略差;二阶滑模控制器的各项性能均优于普通的自适应滑模控制器;对比两种改进的控制方法,自适应滑模控制器在最大输出的性能上更具优势,二阶滑模控制器的稳态最大误差和平均输出的性能则高于滑模自适应滑模控制器,而平均收敛时间的表现两者相同。
4 结 论
结合分数阶微积分性质、自适应控制与有限时间稳定性分析、滑模控制器等知识,成功设计了不同维分数阶混沌系统间的同步控制器,可以在预设时间到达有限时间投影同步。控制器中的自适应律能够逼近内部不确定性和外部扰动范围的上界,使得同步时间不再依赖对干扰的估计。同时针对滑模控制器容易产生抖振的情况,从增加控制结构和改善滑模控制自身两方面入手:首先,根据实际情况统计数据、选择隶属度函数、设计二维模糊控制规则,将设计好的模糊控制与自适应滑模控制结合,提出了模糊自适应滑模控制,可以根据具体系统的表现设计模糊规则;其次,以自适应滑模控制器为基础,将整数阶的SuperTwisting控制律运用到分数阶系统上,使控制器扩展为分数阶系统的二阶滑模控制,由于没有增加额外结构使得控制器的实现更加简单。两种方法无论是从抖振幅度还是抖振频率都对滑模控制进行了削减,并通过仿真对各自性能的优劣进行了分析。
參考文献
[1] KIANIB A, FALLAHI K, PARIZ N, et al. A chaotic secure communication scheme using fractional chaotic systems based on an extended fractional Kalman filter [J]. Communications in Nonlinear Science and Numerical Simulation, 2009, 14(3): 863-879.
[2] KHANZADEH A, POURGHOLI M. A novel continuous timevarying sliding mode controller for robustly synchronizing nonidentical fractionalorder chaotic systems precisely at any arbitrary prespecified time [J]. Nonlinear Dynamics, 2016, 86(1): 543-58.
[3] SHIRKAVAND M, POURGHOLI M. Robust fixedtime synchronization of fractional order chaotic using free chattering nonsingular adaptive fractional sliding mode controller design [J]. Chaos, Solitons & Fractals, 2018, 113:135-47.
[4] MOFID O, MOBAYEN S. Adaptive synchronization of fractionalorder quadratic chaotic flows with nonhyperbolic equilibrium [J]. Journal of Vibration and Control, 2018, 24(21): 4971-4987.
[5] MOHAMMADZADEH A, GHAEMI S. A modified sliding mode approach for synchronization of fractionalorder chaotic/hyperchaotic systems by using new selfstructuring hierarchical type2 fuzzy neural network [J]. Neurocomputing, 2016, 191:200-213.
[6] GAO Like,WANG Zhihui,ZHU Wenji, et al. Modified sliding mode synchronization of typical threedimensional fractionalorder chaotic systems [J]. Neurocomputing, 2015, 166:53-58.
[7] ZHANG Xingpeng, ZHANG Xiaohong, LI Dong, et al. Adaptive synchronization for a class of fractional order timedelay uncertain chaotic systems via fuzzy fractional order neural network [J]. International Journal of Control, Automation and Systems, 2019, 17(5): 1209-1220.
[8] BEHINFARAZ R, BADAMCHIZADEH M A, GHIASI A R. An approach to achieve modified projective synchronization between different types of fractionalorder chaotic systems with timevarying delays [J]. Chaos, Solitons & Fractals, 2015, 78:95-106.
[9] AGHABABA M P, KHANMOHAMMADI S, ALIZADEH G. Finitetime synchronization of two different chaotic systems with unknown parameters via sliding mode technique [J]. Applied Mathematical Modelling, 2011, 35(6): 3080-3091.
[10]LI Chenkuan, LI Changpin. Remarks on fractional derivatives of distributions [J]. Tbilisi Mathematical Journal, 2017, 10(1): 1-18.
[11]POLYA G, HARDY G H, LITTLEWOOD. Inequalities [M].Cambridge:Cambridge University Press, 1952.
[12]李鹏, 郑志强. 基于类二次型 Lyapunov 函數的 Supertwisting 算法收敛性分析 [J]. 控制与决策, 2011, 26(6): 949-952.
[13]MUOZVZQUEZ A J, PARRAVEGA V, SNCHEZORTA A . Uniformly continuous differintegral sliding mode control of nonlinear systems subject to Hlder disturbances [J]. Automatica, 2016, 66:179-184.
[14]TANG Yu. Terminal sliding mode control for rigid robots [J].Automatica, 1998, 34(1): 51-56.

