基于神经模糊网络的分数阶Chameleon系统同步研究

陈嘉乐，赵小山

（天津职业技术师范大学理学院，天津 300222）

分数阶微积分理论起源可以追溯到三个多世纪以前，由于当时计算效率低下，导致其在很长一段时间内只停留在纯数学领域，没有得到人们的重视。随着计算机技术的不断发展与完善，人们发现分数阶微分方程能够更加精确地对实际物理系统建模，有助于准确模拟各种系统的动力学特性，这使得分数阶混沌系统备受关注。现今，人们已经对混沌同步问题进行了广泛的研究，研究人员提出了许多控制方法，如自适应控制[1]、滑模控制（SMC）[2]、有限时间控制[3]等。

Chameleon系统于2017年被提出[4]，其具有一个非常有趣的性质：根据系统中参数的取值，该系统可以没有平衡点，也可以有一系列的平衡点，或者只有1个稳定的平衡点。正是由于该性质让其拥有了Chameleon的名字，也引起了很多研究人员的关注与研究[5-6]，但现阶段关于分数阶Chameleon系统的研究还很少[7]。

由于模糊逻辑和神经网络均具有良好的逼近能力，它们作为智能控制领域的代表，被推广并应用于分数阶混沌系统的各类控制问题[8-9]。采用神经网络的框架实现对模糊系统的设计，结合二者各自的优点，神经模糊网络（neural fuzzy network，NFN）成为一种强有力的控制方法。另一种有效的控制技术是SMC，其也被推广到分数阶系统的稳定性分析和控制器设计中[10-11]。与整数阶SMC相比，分数阶SMC具有跟踪速度快、鲁棒性强等优势。综合上述原因，本文研究了基于NFN和SMC的分数阶超混沌Chameleon系统的同步问题。选取了分数阶滑模函数，设计了控制器和参数自适应律，得到了分数阶超混沌Chameleon系统同步的充分条件。最后通过数值模拟验证了控制效果的稳定性和收敛性。

1 预备知识

定义1Caputo分数阶微积分定义

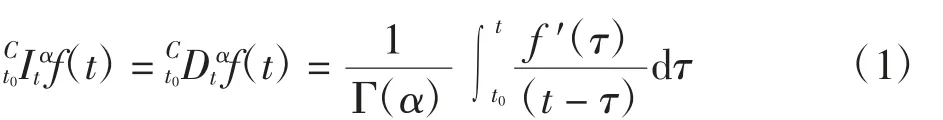
式中：0＜α＜1；t0为初始时刻；Dαf（t）=Ct0Dtαf（t），以下使用的分数阶导数均为Caputo定义下的导数。

性质1分数阶微分满足

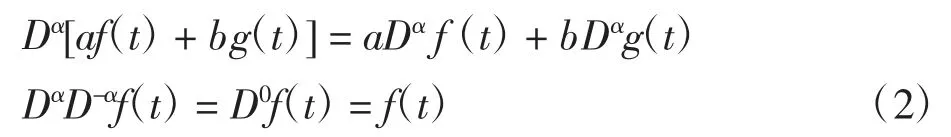
引理1[12]假设x（t）∈R是连续可微函数，P∈Rn×n是一个正定矩阵，那么对于α∈（0，1），满足不等式

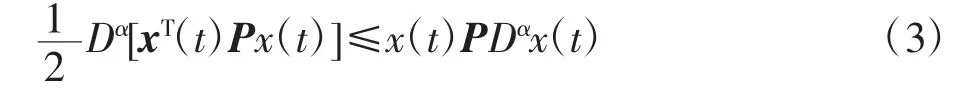
特别地，当x（t）∈R是一个连续可微函数时，可以得到

引理2[13]假设x（t）=0是非自治分数阶系统Dαx（t）=F（x，t）的平衡点，并且存在1个连续的李雅普诺夫函数V（x（t），t）和K类函数χr（·）（r=1，2，3），对∀x≠0，α∈（0，1），使得下列不等式成立

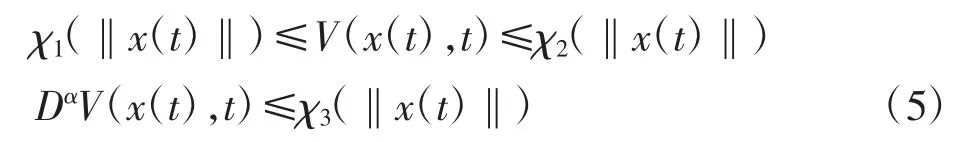
那么，上述分数阶系统在原点是渐近稳定的。

2 分数阶超混沌Chameleon系统

Chameleon系统用四维分数阶微分方程描述为

式中：x1、x2、x3、x4为系统状态变量；a、b为2个常数参数，通过调整参数的值，可以改变系统的动力学行为。

（i）当a=b=0时，系统有1条平衡线。

（ii）当a＞b=0时，系统只有1个平衡点。

（iii）当a＜b=0时，系统只有1个平衡点。

（iv）当a=0≠b时，系统没有平衡点。

选择a=b=0，α=0.98时，分数阶超混沌Chameleon系统的相轨迹如图1所示。

图1 分数阶超混沌Chameleon系统的相轨迹

假设式（6）为驱动系统，则相应的响应系统为

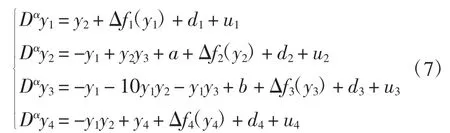
式中：yi为系统状态变量；Δfi（yi）为不确定项；di为外界干扰；ui为待设计的控制器。

同步误差定义为ei=yi-xi，得到误差系统为

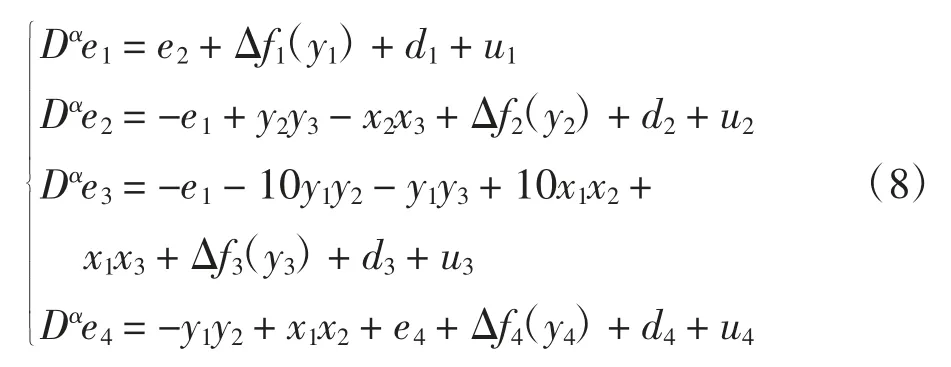
上下文中出现的所有i=1，2，3，4。

3 自适应神经模糊网络滑模同步

3.1 滑模控制器

分数阶滑模面构造为

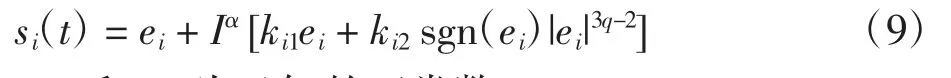
式中：ki1和ki2为已知的正常数；2/3＜q＜1。

根据分数阶SMC理论，当状态轨迹在滑动模式下运行时，必须满足条件s（t）=0和Dαs（t）=0。得到

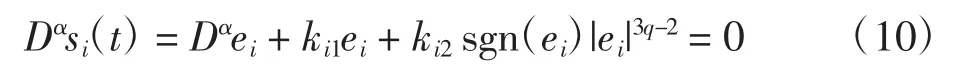
结合误差系统（8）和式（10），可得理想中的等效控制器为

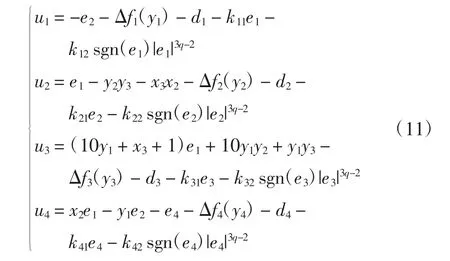
由于有关模型不确定性和外界干扰的信息部分未知或完全未知，故无法实现理想的控制器。因此，采用NFN来估计模型不确定性。

3.2 神经模糊网络

近年来，NFN成功应用在信息处理和控制应用等许多领域中[14-15]，该网络由输入层、隶属函数层、规则层、归一化层和输出层5层结构组成[16]，神经模糊网络结构如图2所示。

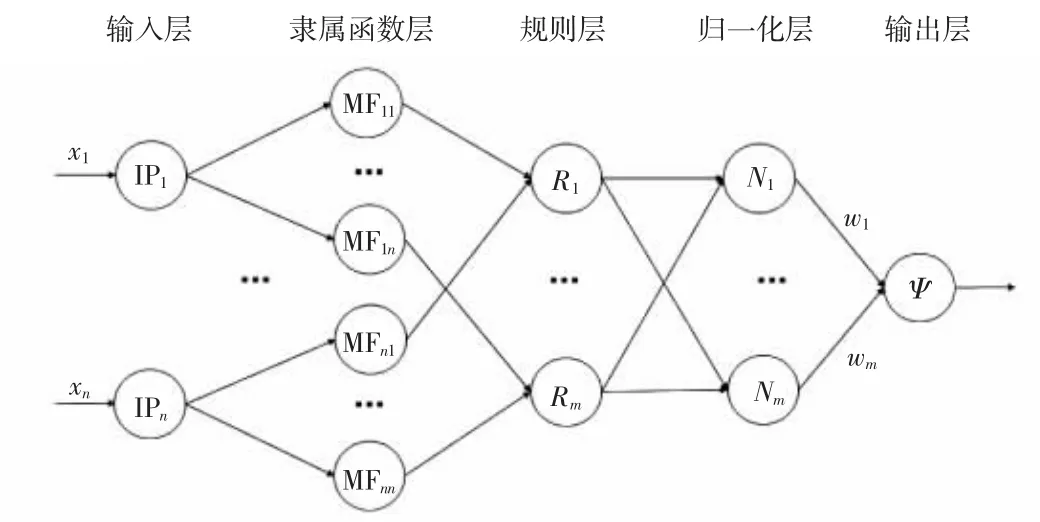
图2 神经模糊网络结构

未知光滑非线性函数可以用NFN的万能逼近定理近似如下[16]

式中：δ为近似误差；W*为参数W的最佳值。

由于实际中无法获得最优NFN，因此使用NFN估计器来估计最优NFN。NFN估计器定义为

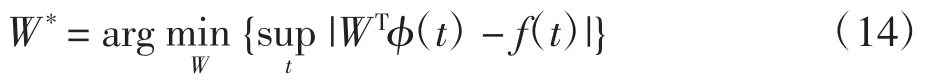
假设1近似误差δ和外界干扰d满足以下条件

式中：λi1、λi2为未知的正参数。

然后，基于NFN的鲁棒控制器可以构造为

自适应参数更新律可以构造为

式中：系数k、ρ、μ皆为已知的正常数。

3.3 稳定性分析

定理1考虑具有不确定性和外界干扰的分数阶Chameleon系统，误差系统如式（8）所示。滑模面、控制器和参数更新律分别设计为如系统（9）、（16）、（17）所示。则系统（6）和（7）取得自适应神经模糊网络滑模（ANFNSMC）同步。

证明将式（12）与（16）代入误差系统（8）得

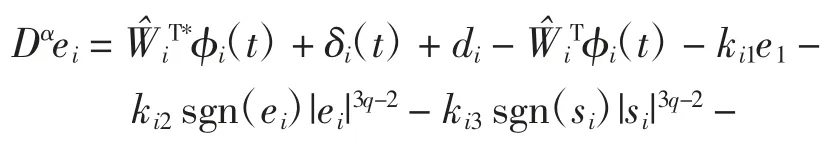
选取以下Lyapunov函数

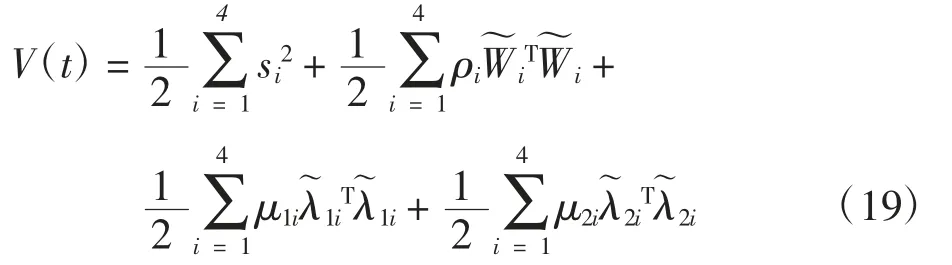
根据引理1对V（t）进行分数阶导数，可以得到

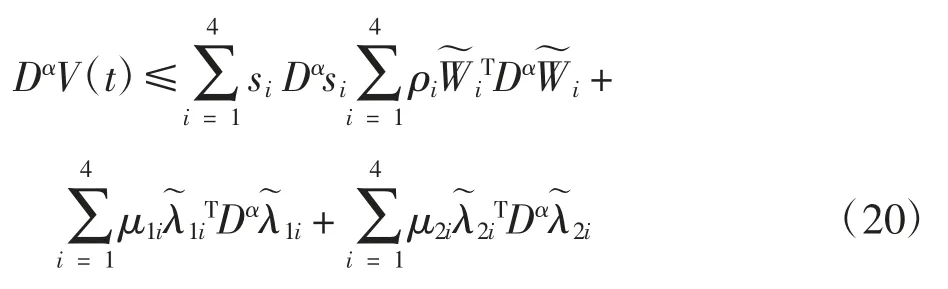
将等式（10）、控制器（16）和参数更新律（17）代入式（20）可得

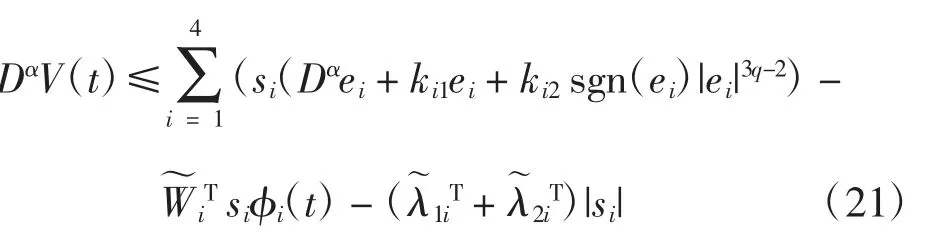
将式（18）代入得

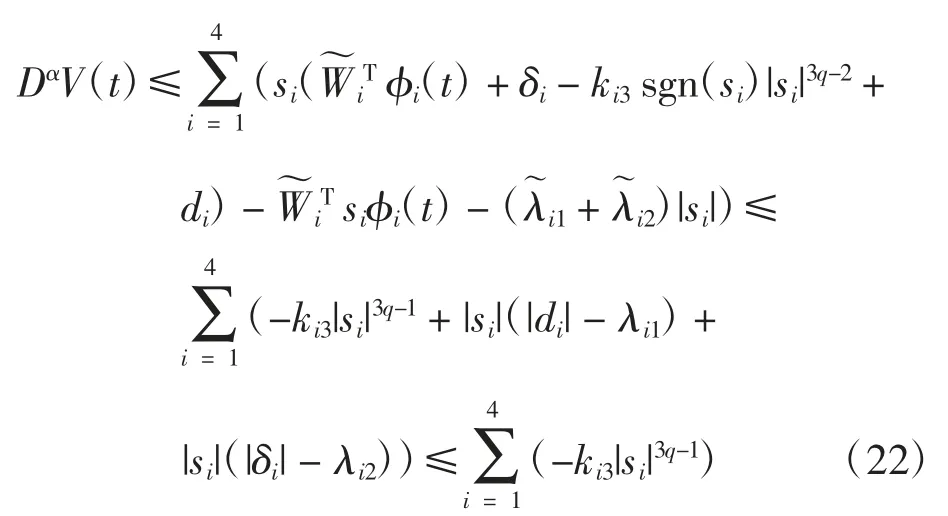
因此，根据引理2，误差系统（8）的系统状态收敛于滑模面。这表明误差系统（8）可以被系统（16）中提出的控制器稳定，进而使得驱动系统（6）与响应系统（7）同步。

4 数值仿真

为了说明ANFNSMC对分数阶Chameleon系统同步的有效性，通过Matlab数值模拟仿真，检验控制器（16）的控制效果。

令系统的初始状态（x1（0），x2（0），x3（0），x4（0））=（0.3，0.5，0.5，0.2），（y1（0），y2（0），y3（0），y4（0））=（-0.2，0.4，0.3，0.5），并选择参数（k11，k12，k13）=（3，5，2），（k21，k22，k23）=（3，5，3），（k31，k32，k33）=（3，5，5），（k41，k42，k43）=（3，5，4），μi1=0.1，μi2=0.2。不确定项和外界干扰项选为

并且对于NFN的每个输入变量，使用高斯隶属函数exp（-（x-ml）2/2nl2），l=（1，2，3，4，5），定义5个模糊规则。输入隶属函数如图3所示。

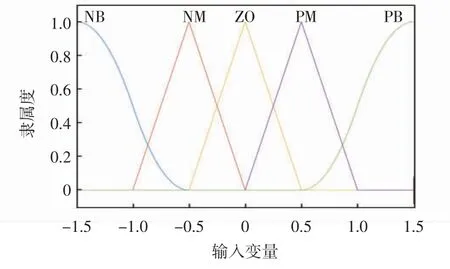
图3 输入隶属函数

所设计的控制器对分数阶Chameleon系统的同步控制结果如图4和图5所示。其中，状态变量同步时间历程如图4所示，图4显示了随着时间的推移，4对变量的同步状态。误差系统时间历程如图5所示，图5显示了随着时间的推移，误差向量快速收敛为0的情况。所有的仿真结果都表明了ANFNSMC在分数阶Chameleon系统同步中的有效性。

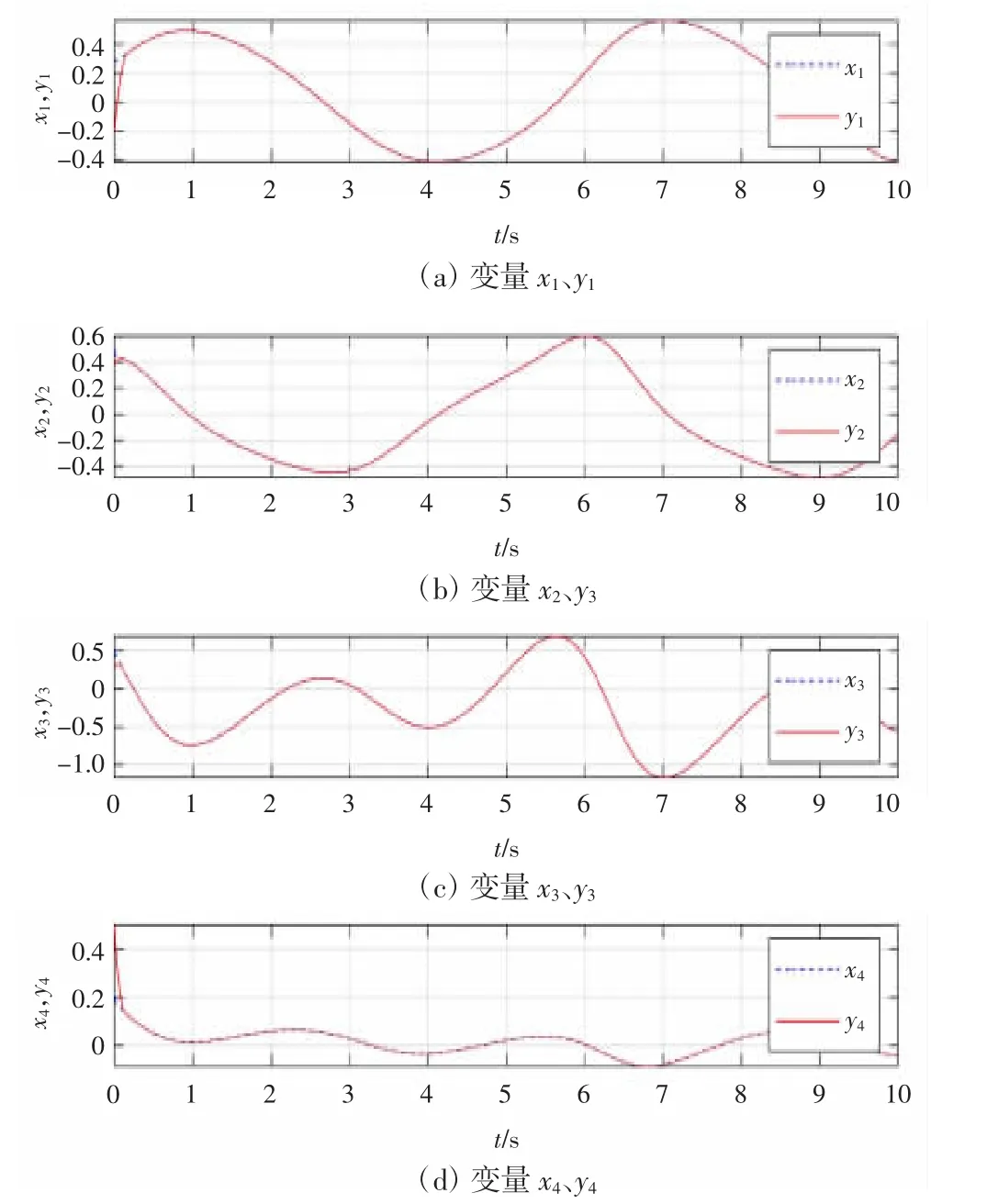
图4 状态变量同步时间历程

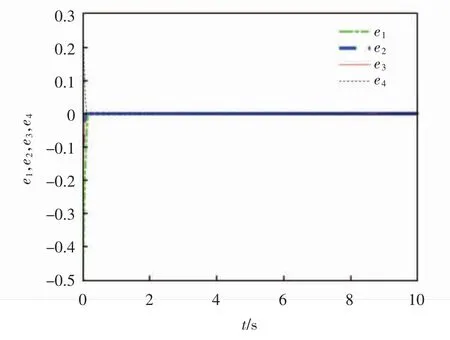
图5 误差系统时间历程

5 结语

本文根据ANFNSMC方法研究了具有不确定性和外部干扰的分数阶超混沌Chameleon系统的同步问题。介绍了分数阶超混沌Chameleon系统的动力学特性，给出同步误差系统。设计出相应的控制器与参数更新律，得到分数阶超混沌Chameleon系统ANFNSMC同步的充分条件。通过数值仿真得到同步误差系统在有限时间内接近0，验证了结论的可行性及控制器的收敛性与鲁棒性。