基于四阶累积量的MUSIC算法性能仿真分析

李丹宁，石和平，曹继华，任 洁

（1.天津职业技术师范大学电子工程学院，天津 300222；2.天津职业技术师范大学汽车与交通学院，天津 300222）

阵列测向，又被称为空间谱估计或到达角（direction of arrival，DOA）估计[1]，DOA估计主要是根据发送无线电信号，以及通过接收入射到阵列传感器上的相位差信息，判断在空中某一范围内的各个目标信号源，从而估计相对传感器阵列发射天线的方位角[2]。当前DOA估计的基础理论和技术正逐步走向成熟，但需要深入研究的方向仍有不少。其中，在阵列信号处理进程中又以Schmidt[3]所提出的多重信号分类（MUSIC）子空间类算法最具代表意义，被誉为DOA空间谱估计中的里程碑。MUSIC算法需要对接收数据的协方差矩阵进行特征分解，并且需预知噪声的特性和信源个数，这些条件在一定程度上限制了其实际应用。随后，Porat等[4]提出了MUSIC-Like算法，也可称为传统的四阶累积量的MUSIC算法。该方法利用四阶累积量与子空间方法结合，进行阵列信号的测向研究。Dogan等[5]推导出了四阶累积量抑制噪声的原理。文献[6-7]的研究则放宽了对信源数目的限制，验证了四阶累积量在实际阵列中所具备的特性。文献[8-10]也表明四阶累积量可以有效去除矩阵中的冗余元素。近些年来，科研人员对信号测向的研究层出不穷，同时四阶累积量在DOA估计中也得到越来越多的应用[11-17]。本文基于四阶累积量在阵列信号测向处理中的应用研究，根据文献[4-6]建立阵列窄带远场信号的接收模型，介绍四阶累积量的MUSIC算法[4]的基本原理，分析四阶累积量矩阵的处理过程，并通过扩展阵列孔径[18]，使接收阵元数据得到充分利用，同时测得来波方向≥阵元数的信号。在不同的参数下，对该算法进行仿真，分析不同参数背景下该方法的估计性能。

1 窄带信号接收模型及算法原理

1.1 信号接收模型与MUSIC算法

假设在空间里有N个传感器构成的均匀等距直线阵列，存在M个远场窄带独立信源sl（t）（l=1，2，…，M）作用到该阵列上，该阵列的第i个接收数据的信号模型可以表示为

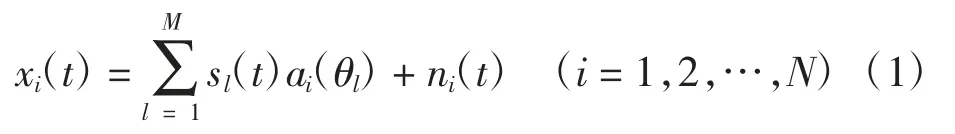
式中：ni（t）为第i个传感器阵元上的高斯白噪声，其均值为0，方差为σ2；ai（θl）则为第i个传感器阵元对第l个入射信号的空间响应。ai（θl）的表达式为

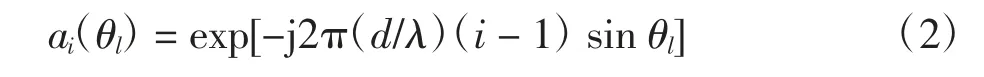
式中：d为该均匀直线线阵阵元之间的间距；λ为中心频率f0的远场窄带信号所对应的波长。

将N个传感器阵元所接收的数据构成一组列向量，表示成矩阵形式为

式中：X（t）=[x1（t），x2（t），…，xN（t）]T为传感器阵元接收到的N×1维的数据矢量；S（t）=[s1（t），s2（t），…，sM（t）]T则是M×1维的入射信号矢量；N（t）=[n1（t），n2（t），…，nN（t）]T为N×1的阵元上的噪声矢量；A=[a（θ1），a（θ1），…，a（θM）]T为N×M维来波信号所对应的导向矢量阵列流形矩阵。

对于零均值的阵列信号入射源，其接收阵列的信号数据的协方差矩阵可表示为

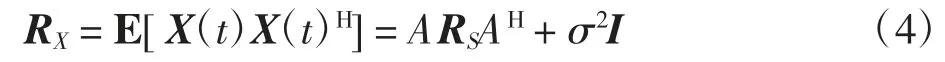
式中：E为数学期望的符号；RS为阵列接收入射信号数据的协方差矩阵E[S（t）S（t）H]；I为N阶的单位矩阵；H为共轭转置操作。

传统MUSIC算法[3]是对数据协方差矩阵进行特征分解，进而通过空间谱估计中谱峰搜索估测入射信号的来波角度。对式（4）中阵列的协方差矩阵进行特征分解有

式中：US为信号子空间；UN为噪声子空间。

在实际DOA估计中是以最小化优化搜索实现的，故MUSIC算法的空间谱估计公式为

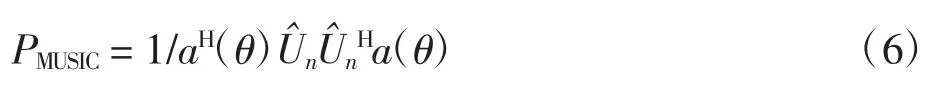
1.2 四阶累积量

假设接收数据X（n）为N维零均值的复平稳随机信号，那么该信号的四阶累积量需满足：

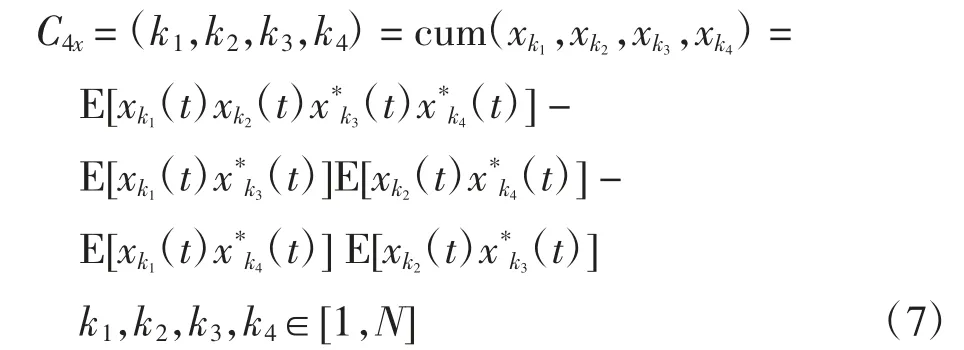
式中：cum为求累积量；*表示共轭符号。

显然，四阶累积量cum（k1，k2，k*3，k*4）随着k1、k2、k3、k4的变化，共有N4个值。为了方便操作，可以将该信号的四阶累积量的N4个值存入下面定义的N2×N2矩阵C4。

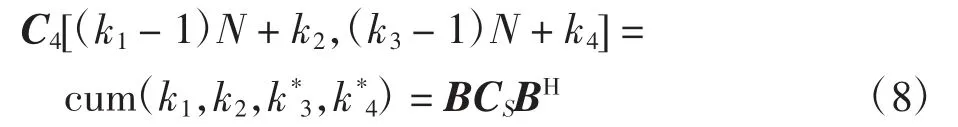
式中：CS为入射来波信号的四阶累积量矩阵；B为阵列扩展的阵列流形矩阵，该扩展阵列的表达式为

式中：○×为Kronecker积。

B矩阵中的每一列可表示为

式中：列向量b（θ）为扩展的阵列流形，由上述的Kronecker的积性质可得；b（θ）为N2×1维矢量，相对于a（θ）而言，其维数实现了扩展N倍，则便可估测窄带信源数≥阵元数的入射信号。

1.3 四阶累积量MUSIC算法

四阶累积量MUSIC算法[4]是通过用四阶累积量矩阵C4来替代协方差矩阵RX，对矩阵C4进行特征分解，并结合MUSIC算法，进行谱峰搜索即可估测出来波方向，具体步骤如下：

步骤1将阵列接收的信号数据模型式（1），按照累积量矩阵的式（7），构造四阶累积量矩阵C。

步骤2将矩阵C按式（5）进行特征分解，找到其相对应的特征值以及特征值所对应的特征矢量。

步骤3由矩阵C的特征值，判断入射信号源的数目，求出四阶信号子空间和噪声子空间。

步骤4针对所得信号参数的范围，结合MUSIC算法按式（6）进行谱峰搜索即可测出来波方向。

2 仿真分析

2.1 算法的比较

实验基于四阶累积量的MUSIC算法与传统MUSIC算法进行仿真，针对窄带远场信号进一步分析了2种算法的估计性能。设置10个阵元数，选取入射到传感器阵列的角度分别为-20°和20°，信号频率取值分别为π/4和π/6，SNR=0 dB，阵元的间距d=0.5λ，设置的快拍数为1 024，此时的噪声为高斯白噪声。2种算法仿真效果对比如图1所示。

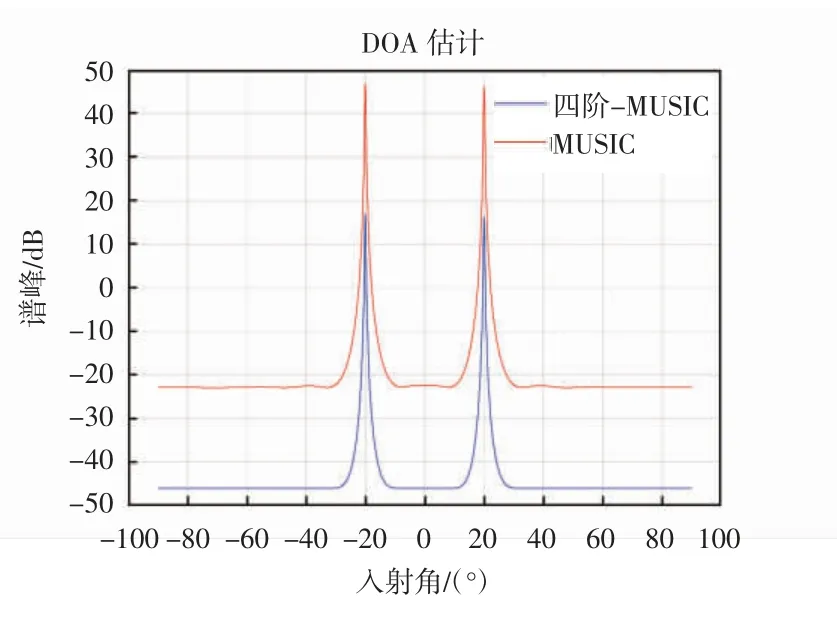
图1 2种算法仿真效果对比

从图1可知，四阶累积量的MUSIC算法[4]谱峰更尖锐，阵列测向的角度估计性能较好。相比较于MUSIC算法[3]，由于高斯噪声三阶及以上的累积量恒为0，故能够更好地改善MUSIC算法的性能。

2.2 多信源数对四阶累积量MUSIC的影响

仿真实验取阵元数为4，信号源为6个独立不相关的远场窄带信号。来波方向分别在-60°和60°之间均匀分布，信号频率为π/6，信噪比均为0，传感器阵元之间的间距取0.5λ，实验快拍数为1 024，信号为高斯白噪声。多信号源的DOA估计如图2所示。

从图2可知，此实验中的阵元数目小于信源数，在该仿真实验下，四阶累积量MUSIC算法在多输入信源条件下依然能很好地分辨出信号的波达方向。实验结果表明，该算法没有阵列孔径的损失，并且通过阵列孔径的扩展，放宽了对信源数目的要求。

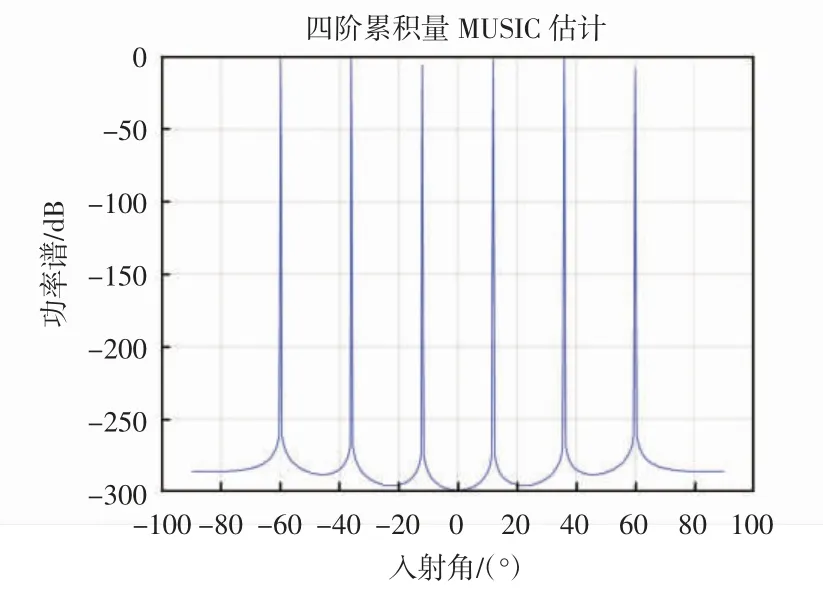
图2 多信源的DOA估计

2.3 不同阵元间距对四阶累积量MUSIC的影响

仿真实验设置选取10个阵元，阵元间距分别为0.1λ、0.5λ、0.8λ。来波角度分别是-20°和20°的独立不相关的远场窄带信号，信号的频率分别选取为π/4和π/6，SNR=10 dB，仿真实验的快拍数为512，噪声为高斯白噪声。不同阵元间距的DOA估计如图3所示。

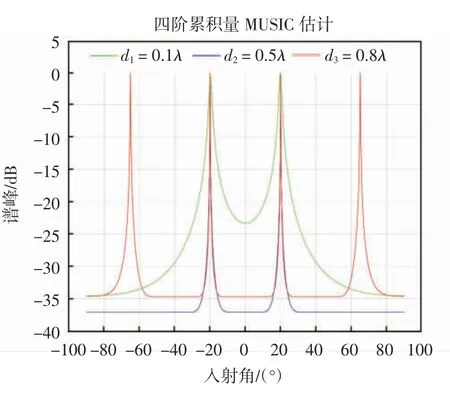
图3 不同阵元间距的DOA估计

从图3可知，当传感器阵元间距为0.5λ时，该算法的波达方向估计性能相对最好。当阵元间距为0.1 λ时，该算法可以估计出来波角度，但其旁瓣部分较大，性能较之阵元间距为0.5λ有所下降。当阵元间距为0.8λ时，空间谱出现混叠现象，但是旁瓣部分的谱峰较之阵元间距为0.1λ时明显得到抑制，更好地突出了其有效抑制高斯噪声的特性。因此，在实际空间测向中，选取合适的阵元间距可以使算法更好地估计入射角度。

2.4 快拍数对算法精度的影响

仿真实验设置6个阵元，传感器阵元之间的间距取0.5λ。来波角度分别为-20°和20°的独立不相关的远场窄带信号，信号的频率分别为π/4和π/6，SNR=10 dB，仿真实验的快拍数分别为10、100、1 000，噪声为高斯白噪声。另外，根据选取的快拍数10～1 000，对每次信号角度的估计值进行500次蒙特卡罗仿真，DOA估计精度如图4所示，归一化成功概率随快拍数变化情况如图5所示。

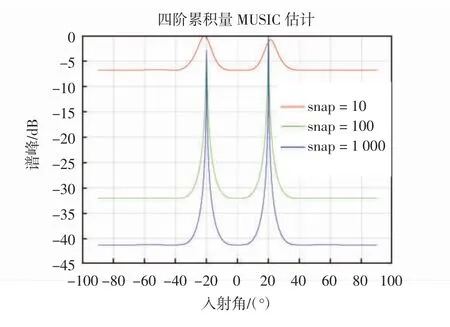
图4 不同快拍数的DOA估计

图5 归一化成功概率随快拍数变化情况

从图4可知，当快拍数=1 000时，本文分析的四阶累积量MUSIC算法估计性能较好。快拍数=10时，其谱峰不是特别尖锐。从图5可知，当快拍数为100时，归一化成功概率出现转折，在快拍数＞100后，随着快拍数目越来越多，该算法的归一化概率趋于稳定，达到估计的理论值，但其计算量也随之增加，因此需要在实际的估计中选择合适的快拍数。

2.5 信噪比对算法精度的影响

仿真实验取阵元数为6，阵元间距为0.5λ。来波角度分别为-20°和20°的独立不相关的窄带信号，信号的频率分别设置为π/4和π/6，SNR分别为-5 dB、10 dB、25 dB，快拍数为512，噪声为高斯白噪声。另外，信噪比设置为5个间隔单位，选取范围为-5～25，并对每次选取的估计值进行500次蒙特卡罗仿真，DOA估计精度如图6所示，归一化成功概率随信噪比变化情况如图7所示。

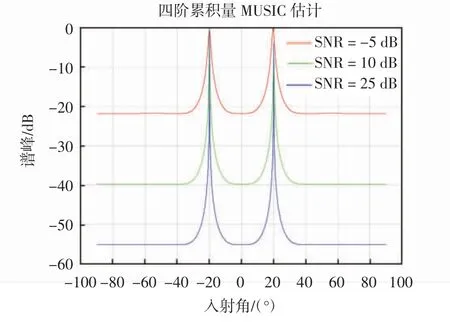
图6 不同信噪比的DOA估计

图7 归一化成功概率随信噪比变化情况

从图6和图7可知，该算法在低信噪比SNR=-5 dB时，依然可以分辨出来波方向。而当信噪比≥0时，归一化成功概率趋于理论估计值。随着信噪比取值的增加，本文介绍的四阶累积量结合MUSIC算法的阵列估计性能越来越好，并且谱峰搜索效果也很尖锐，这说明该算法DOA估计的角分辨率效果越好。但是，当信噪比达到一定值时，其估计性能会达到该算法的理论估计值。

3 结 语

本文介绍了一种结合四阶累积量的DOA估计技术，即四阶累积量MUSIC算法。该算法充分利用了扩展的阵列孔径，有效地估计出多于阵元个数的入射信号源。通过对比MUSIC算法的估计性能，说明该算法可以更好地估计来波角度，提高了阵列处理方法的分辨效率。此外，本文在不同阵元间距、快拍数和信噪比条件下，对算法的估计性能进行了仿真分析。研究结果表明，在实际阵列设计中，为降低运算的复杂度，应选取合适的参数，以实现更高的DOA估计的空间分辨率。