三相四桥臂混合五电平逆变器及其3D-SVPWM 算法

魏金成，杨 鑫，邱晓初，李 琴

（西华大学电气与电子信息学院，成都 610039）

400 Hz 中频电源常被用于军用及航空等领域，与传统的两电平电压源逆变器相比，多电平逆变器输出电压呈准正弦，dv/dt 更低，电流纹波更小[1-6]。然而，多电平逆变器也有一些明显的缺点，如开关器件数量多、所需直流电源过多和调制算法复杂等，因此，研究减少开关器件和直流电源数量及调制算法显得十分重要[7-8]。

为了用更少的开关器件实现更多的输出电平，混合多电平的概念被提出。文献[9]提出了一种准Z源混合多电平逆变器，可实现9 个电压等级输出，提高了电压增益，但其电容电感数量多、拓扑结构复杂；文献[10]提出了一种带可切换电容单元的混合型多电平逆变器，它可以使电压增益加倍，增加输出电平数，并且不需要复杂的方法来平衡电容电压，然而，这种结构可以提高的电压增益是有限的。通过调整直流端电压比例，可以获得更多的输出电压等级[11-12]，但由于所使用的直流电源不同，增加了调制算法的复杂性。

文献[13-16]中四桥臂逆变器SVPWM 算法大多是基于αβγ 坐标系，这种调制算法必须进行坐标系的转换，这也意味着复杂的计算。此外，在αβγ 坐标中的三维坐标相对于abc 坐标系更难于理解。文献[17]将abc 坐标系下的3D-SVPWM 算法首次应用于三相四桥臂逆变器，降低了复杂度和计算量，与传统2D-SVPWM 算法相比，3D-SVPWM 算法不涉及三角函数和坐标转换等计算，减少了相应的计算量，这些都是重要的优势；文献[18]提出了一种非常简洁的四桥臂多电平逆变器3D-SVPWM 算法，该算法计算成本低，且与逆变器的电平数无关，但当直流端电压不平衡时，电压矢量形成的三维空间就不再是对称的，矢量四面体就不再是规则的，因此该算法不能直接应用于不对称三电平四桥臂的3D-SVPWM 算法；邱晓初等通过将直流端电压比例调整为2∶1，弥补了abc 坐标系下3D-SVPWM 算法的欠缺，提出了新的四面体划分方式，解决了不规则四面体的划分问题[19]，但该算法并未采用最优的四面体划分，因此造成了开关管应力较大的问题。

虽然对于直流端电压不平衡的多电平逆变器的研究已经很成熟[20-22]，但是利用SVPWM 算法控制直流侧电压不平衡的逆变器的研究还很少。因此，本文对abc 坐标系下的3D-SVPWM 算法进行了深入研究和改进，以解决直流电压不平衡的多电平逆变器调制问题。本文的主要贡献是在abc 坐标系下，通过对不规则立方体的剖分，有效解决了非对称四桥臂逆变器在abc 坐标系下的3D-SVPWM算法中四面体剖分困难的问题，实现了低电平拓扑下的高电平输出，并且其电压应力更低，进一步完善了abc 坐标系下的3D-SVPWM 算法。

1 三相四桥臂混合五电平逆变器拓扑结构及工作原理

图1 为本文所提的混合五电平逆变器拓扑结构，由4 个完全相同的对称桥臂组成，每相桥臂均含有6 个开关管，其中Sk1、S'k1，Sk2、S'k2和Sk3、S'k3（k=a、b、c、n）为互补的3 对开关管，其输入直流端采用3个不完全相同的电容串联。表1 给出了8 种不同的开关状态所对应的输出电压等级。其中1 表示开关管是开通状态，0 表示开关管是关断状态。

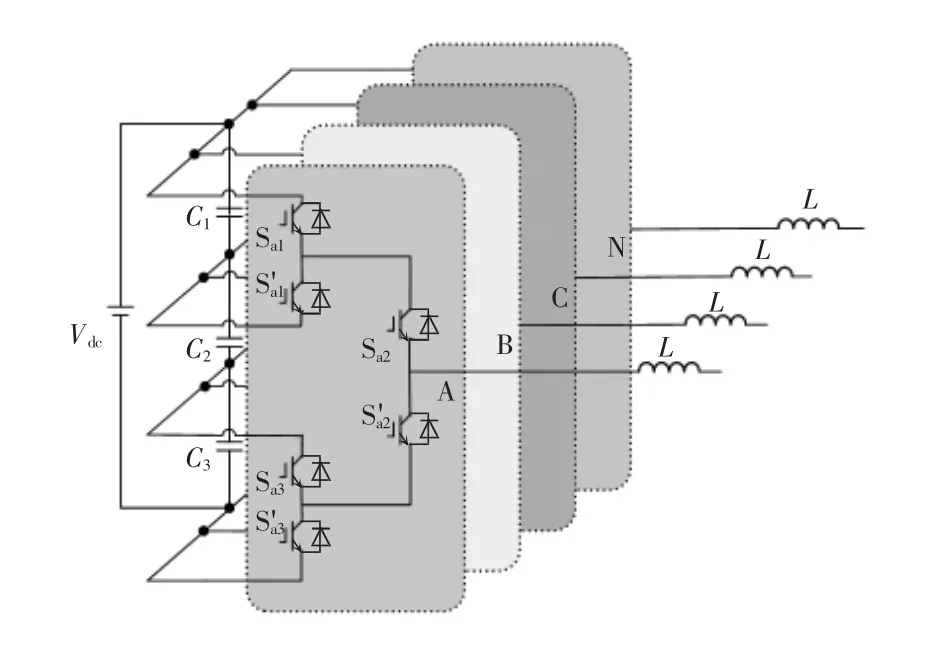
图1 非对称三相四桥臂五电平逆变器拓扑结构Fig.1 Topology of asymmetrical three-phase four-leg five-level inverter

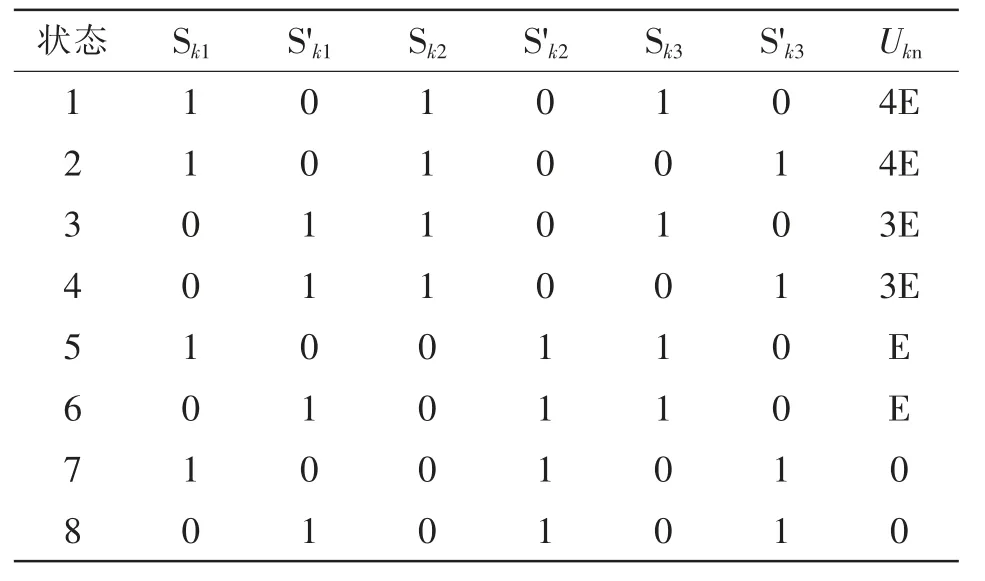
表1 每个桥臂开关状态（k=a、b、c、n）Tab.1 Switching states of each leg（k is a,b,c,or n）

图2 为a 相桥臂不同开关状态对应的工作状态，由表1 可知，8 种不同的状态对应4 种不同的输出电压，每种输出电压均含有1 种冗余状态。以输出相电压为4E 为例，状态1 和状态2 输出均为4E，但状态1 的Sa'2的电压应力为3E，相较于状态2降低了E，电压应力更低。因此在调制时，将状态2舍去，保留较低电压应力的状态1。同理，可得到另外3 种工作状态：状态3、状态6 和状态8，去掉4种（2、4、5、7）具有高电压应力的冗余模式。将a 相与n 相的工作模式相结合，可以得到16 种不同的工作状态。表2 为a 相与n 相组合后的工作模式及输出线电压，可输出±4E、±3E、±2E，±E，0 共9 个电压等级。

表2 k 相和n 相桥臂相结合（k=a、b、c、n）Tab.2 Combination of phase-k and phase-n legs（k is a，b，c，or n）

图2 a 相桥臂不同开关状态对应的工作状态Fig.2 Working states of phase-a leg corresponding to different switching states

2 abc 坐标下的混合五电平3DSVPWM 算法

基于abc 坐标系的3D-SVPWM 算法将参考电压矢量归一化后，定位到十二面体的一个小四面体中，以确定最近4 个矢量的开关状态。参考矢量所在立方体的定位由两步来实现：一是大立方体或五面体的定位；二是小立方体的四面体定位。混合五电平的矢量空间如图3 所示，其中每个点代表一个矢量。

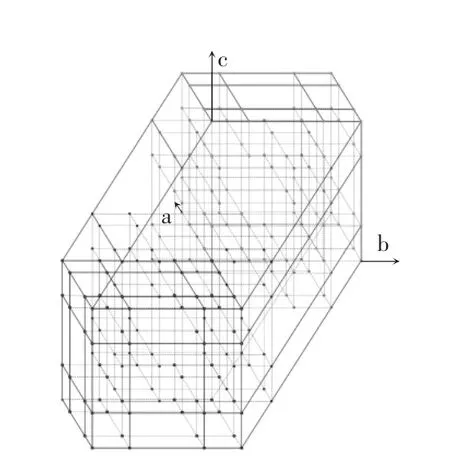
图3 混合五电平的向量空间Fig.3 Vector space of hybrid five-level

整个矢量空间上形成了一个由2 个大立方体和6 个大五面体所构成的十二面体，如图4 所示。由于不对称结构所引起的矢量缺失，因此在立方体和五面体内包含有大量不规则以及不完整的立方体。

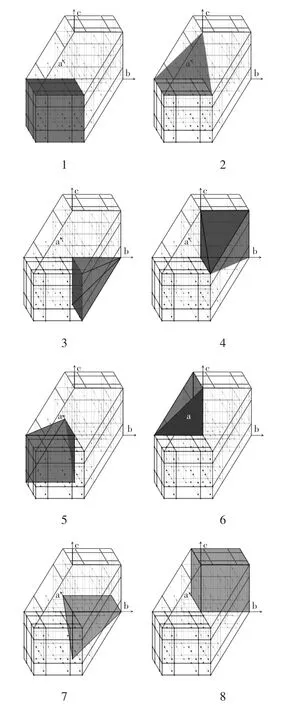
图4 空间十二面体划分Fig.4 Division of 12-hedrons in space

2.1 参考电压定位

将参考向量归一化可得

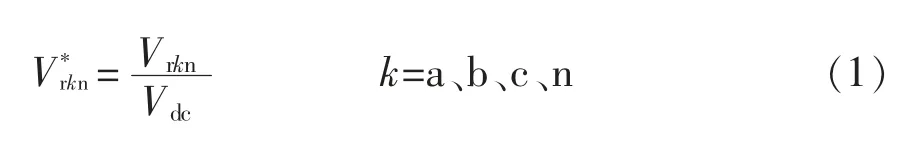
通过坐标原点的平移和参考向量的归一化及取整，只需简单判断的正负性即可完成参考矢量所在大立方体或五面体的定位，也即通过参考矢量的方向确定其所在空间十二面体位置，具体划分方法见表3。

表3 判断参考电压矢量所在的大立方体或五面体Tab.3 Judgement of large cube or pentahedron where the reference voltage vector is located

2.2 四面体的划分和定位

四面体划分遵循abc 坐标系下的划分原则，从等效原点开始，沿对角线进行划分，共有76 种划分结果，如图5 所示。由于矢量点存在缺失，因此在对四面体进行划分时，无法按照标准结构下的划分方式进行。本文提出的混合五电平结构的不规则矢量多边形可分为两类：其一是矢量点位于多面体棱边，如1～7 号小立方体所在的多面体，当矢量点位于其棱边上时，需要通过坐标平移将等效原点平移之后，再进行进一步划分，如5～7 号小立方体；其二是矢量点位于多面体表面，如23～34 号小立方体所在的多面体，当有矢量点位于多面体表面时，需要将多面体划分为两个部分，使得位于表面的矢量点转换为位于棱边上的矢量点，通过坐标平移思想划分小立方体后，每个四面体的顶点均包含等效原点。最后，利用平移后的坐标进行矢量合成。

与大立方体的定位方式相同，小立方体同样通过归一化后的参考矢量值的大小来确定。如当参考电压矢量落入2 号立方体后，若，则参考矢量位于77 号小四面体；反之，当时，则参考矢量位于78 号小四面体内。其中，当且时，所构成的立方体为一个不规则的六面体，如图5 右部分所示，其内部包含多个矢量点，因此对其进行进一步划分并定位，以71～76 号小立方体为例，定位方式如图6 所示。该定位方法仅需要简单的比较运算即可得到结果，不存在三角函数以及坐标变换等增大计算量的步骤，大大降低计算负担。

图5 四面体的划分Fig.5 Division of tetrahedrons

图6 四面体判断流程Fig.6 Judgment process of tetrahedron

2.3 开关矢量动作时间计算

一旦确定了合成参考矢量的4 个基本矢量，则可进行矢量动作时间计算。合成参考向量的4 个顶点的三维空间坐标分别为：。动作时间分别为d1Tm、d2Tm、d3Tm、d4Tm；系统的采样时间为Tm；电压归一化后的参考值分别为

根据伏特平衡的原则，有

通过求解上述线性方程组，即可得到动作时间，并且整个过程中只包含基本的代数运算，大大降低了算法的复杂度。由于其他立方体的基本向量与第2 个立方体的向量分布相同，四面体划分方法相同，解出的小立方体基本向量的作用时间只需通过坐标变换作用于其他扇区的立方体即可。

2.4 基本向量动作序列

由于直流电压不平衡以及一些基本的开关矢量缺失，在基本矢量排序时不能完全实现最优切换。本文使用对称的七段式向量分布序列合成参考电压,并且采用小矢量首发，矢量状态分配如图7所示。混合五电平的基本矢量动作序列如表4 所示，以2 号大立方体的1 号小立方体为例，表中0、1、2、3、4 分别表示输出电压为0、E、2E、3E、4E。

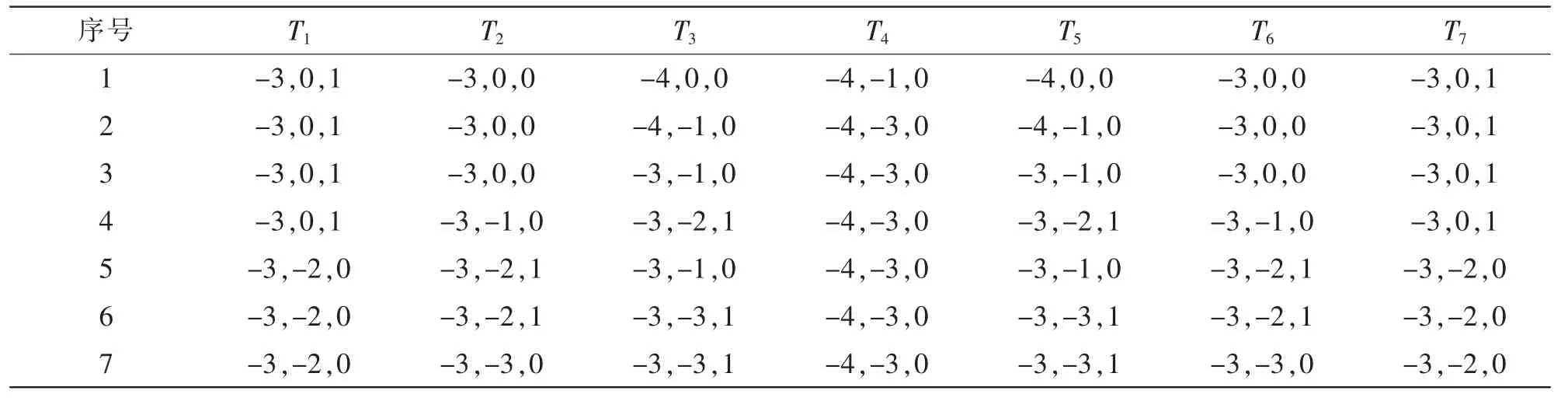
表4 基本向量动作序列Tab.4 Sequence of basic vector actions

图7 向量状态的时间分布Fig.7 Time distribution of vector states

3 仿真验证

为了验证本文提出的abc 坐标系下混合五电平拓扑及其调制算法的正确性,以及其作为中频逆变电源的可行性,在Matlab/Simulink 中搭建了仿真模型，其控制流程如图8 所示，其中直流电源Vdc=200 V；输出参考电压Vref=115 V；采样时间Ts=10 μs；分压电容C1=1 100 μF 和C2=2 200 μF；滤波电路采用12 mH 电感以及2.2 μF 电容；负载采用60 Ω 电阻。

图8 控制流程Fig.8 Flow chart of control

图9 的仿真结果表明，在400 Hz 工作频率下，其他参数相同时，本文提出的混合五电平逆变器在调制比为0.54 时可以输出9 个等级的线电压电平。与传统四电平结构输出相比，混合五电平多了2 个电压电平输出，进一步降低了开关管的应力。

图9 a 相电压与输出电压对比Fig.9 Comparison between phase-a voltage and output voltage

图10 为四电平结构和混合五电平结构的负载输出端电压傅里叶分析结果。混合五电平结构相较于四电平结构的THD 值由1.25%降低到0.87%，其直流偏置得到明显降低，幅值由原来的0.50%降低到0.02%，提升了直流电压的利用率。

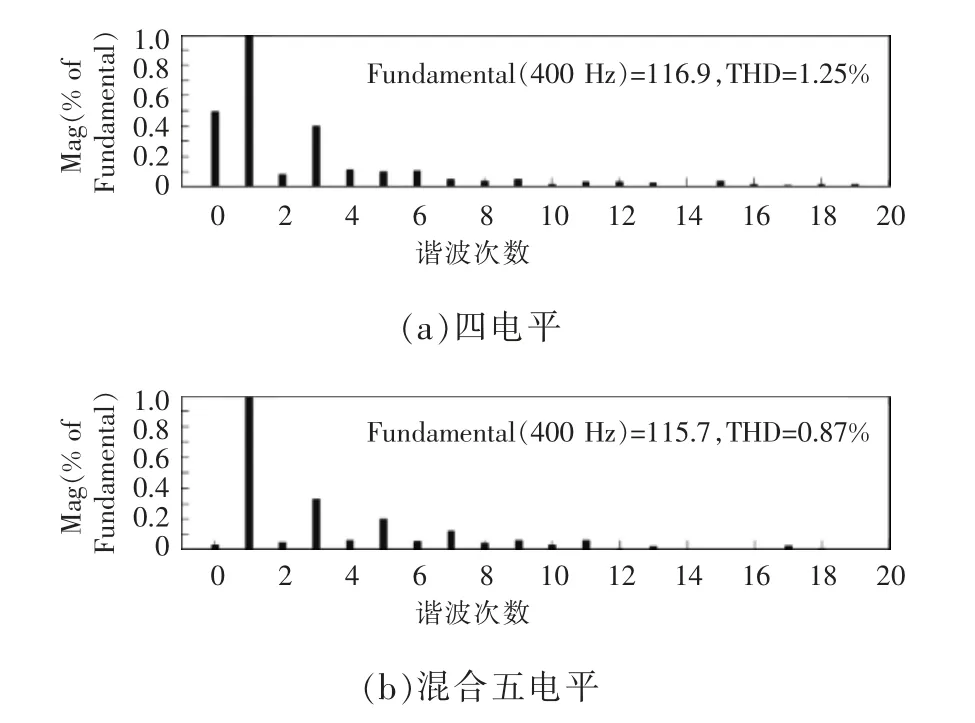
图10 输出电压FFT 分析Fig.10 FFT analysis of output voltage

为了进一步验证所提算法的可迁移性，在50 Hz工频条件下进行了仿真。

图11 为混合五电平在50 Hz 参考值下的输出电压，可以明显看出，所提算法在50 Hz 也有明显的5 个电平，输出波形较好。

图11 混合五电平50 Hz 时a 相电压和输出三相电压Fig.11 Phase-a voltage and three-phase output voltage with hybrid five-level and at 50 Hz

图12 为50 Hz 输出电压的FFT 分析结果，其输出电压谐波失真率仅为0.68%，进一步证明了算法的可行性以及可移植性。

图12 混合五电平输出电压50 Hz FFT 分析Fig.12 FFT analysis of output voltage with hybrid five-level and at 50 Hz

4 实验验证

为了进一步验证本文所提拓扑结构和3DSVPWM 算法的正确性和可行性，搭建了与仿真参数相同的实验平台，如图13 所示。控制器芯片采用TMS320F28335，驱动电路采用2SC0108T2A0-17，开关器件采用F50R12RT4 型IGBT 模块，IGBT 开关频率为10 kHz，三相电压有效值为115 V，频率为400 Hz，其余参数与仿真相同。

图13 实验平台Fig.13 Experimental platform

图14 和图15 分别为400 Hz 滤波前的四电平输出线电压和混合五电平a 相输出线电压，可以看出，混合五电平结构的输出电压明显优于四电平结构，其结果与仿真相同。

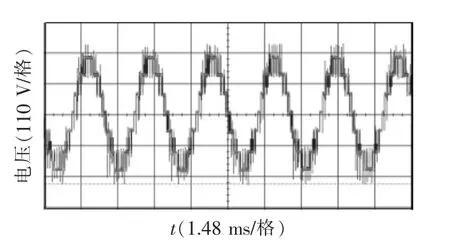
图14 四电平输出线电压Fig.14 Output line voltage with four-level

图15 混合五电平输出线电压Fig.15 Output line voltage with hybrid five-level

图16 和图17 分别为四电平和混合五电平滤波后的三相电压和a 相电流，可以看出，混合五电平结构的输出结果明显优于四电平结构，其波形质量相较于四电平结构更优。

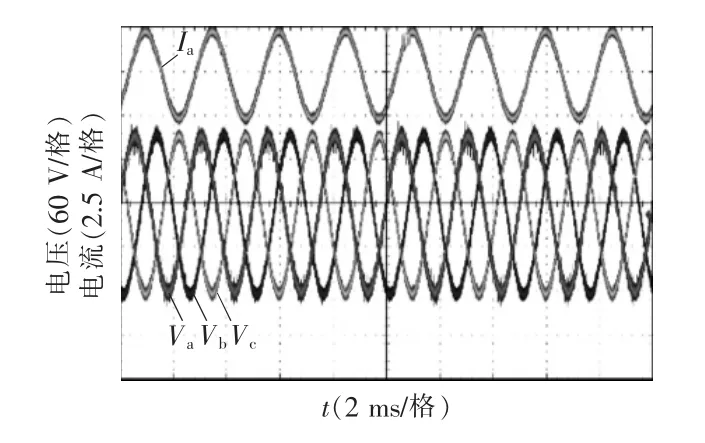
图16 四电平的输出相电压和a 相电流Fig.16 Output phase voltage and phase-a current with four-level

图17 混合五电平的输出相电压和a 相电流Fig.17 Output phase voltage and phase-a current with hybrid five-level

为了进一步对比分析混合五电平结构与四电平结构的输出波形质量，利用WT1800 分析仪对输出电压进行谐波分析，结果如图18 和图19 所示。

图18 FFT 四电平实验结果Fig.18 FFT experimental results with four-level

图19 混合五电平的FFT 实验结果Fig.19 FFT experimental results with hybrid five-level

结果表明，混合五电平的输出波形比四电平的输出波形更好，且谐波失真率降低。通过FFT 分析，得出谐波失真率混合五电平输出的负载电压从四电平的6.84%降低到3.81%，高频分量的最大幅值由5.27%降低到0.22%，明显优于四电平结构。

5 结语

本文首先对三相四桥臂混合型五电平逆变器的工作原理进行分析，采用与传统四电平一致的拓扑，通过改变直流端电流的电压从而增加输出电平数，此拓扑结构的优势在于，在同样的结构下可以输出更多的电平数。然后，对传统abc 坐标系下的3D-SVPWM算法进行深入分析和优化，有效弥补了传统算法难以用于非对称结构下由于矢量缺失导致的立方体定位与四面体划分。最后，通过仿真和实验验证了优化算法的可行性，且该方法可应用于其他非对称结构，具有可推广性。