新型扭簧电连接器的确信可靠性正向设计优化
康锐 刘浩然 张清源 余丽 翟国富
(1. 北京航空航天大学 可靠性与系统工程学院, 北京 100083; 2. 可靠性与环境工程技术重点实验室, 北京 100083;3. 北京航空航天大学 航空科学与工程学院, 北京 100083; 4. 哈尔滨工业大学 电气工程及自动化学院, 哈尔滨 150001)
电连接器是用于传输信号、接通电流的关键器件,其性能降级或失效对整个系统都有重要影响。 近年来,扭簧电连接器因载流改善能力强、接触力稳定性高,在追求小型化、大电流可靠传输的市场中广受关注[1]。 由于存在较高的技术壁垒,要在国产材料、工艺条件下实现扭簧结构,同时满足对竞品低成本的竞争优势,必须要开展多次迭代的概念、结构和详细方案的正向设计,自主研发经济可靠的新型扭簧电连接器。
当前,电连接器的设计主要是在少数理论分析的基础上,以优化性能为目标。 一种常见的设计思路是先参考传统型号的经验结构给出设计图稿[2],再利用经验模型、手册指南等进行理论分析和性能建模[3],之后基于经验取值和区间范围进行实验设计(DOE)和仿真[4-5],最后通过试验测试分析变量的不确定性影响,从而改进设计和控制工艺[6]。 例如,不同学者基于DOE 方法针对材料组合、结构尺寸和工艺公差中少数设计变量进行参数化建模与仿真[7-8]。 文献[9]基于接触电阻模型磨损方程等先后开展了某型片簧电连接器材料、结构的设计优化。 这些设计方法虽能在一定程度上实现电连接器的功能性能设计,但通常无法在设计中保证批量产品在复杂工作环境下的可靠性,且设计过程存在许多经验性的、主观的判断,仍然可能带来失效风险。
为了在新型扭簧电连接器正向设计过程中充分考虑可靠性因素,必须对其进行可靠性正向设计优化。 然而,由于新型扭簧电连接器工艺过程的创新性与结构原理的复杂性,其可靠性正向设计主要面临2 方面挑战:
1) 新型扭簧电连接器是复杂弹性体结构,设计变量众多,交互作用复杂,对可靠性影响形式多样,方案优选的难度大。 正向设计需要同时考虑从原料采买到加工装配整个过程,往往存在多维离散-连续变量[10],而现有方法往往是针对某一种或某几个设计变量的设计,并非系统化和全局化的设计,效率低、成本高及优化空间小。
2) 新型扭簧电连接器采用新工艺过程和新加工设备实现小尺寸加工,且面临复杂工作环境,可靠性受选材、工艺、手册标准、外界环境及工作条件等多源不确定性影响[11],而现有研究通常只考虑其中部分因素的不确定性,模型不完整。 这在缺乏认知、工艺不成熟及需求复杂多变的正向设计中无法基于设计方案得到产品在不同工作场景下的可靠性指标,易导致设计偏差,造成潜在失效风险。
因此,针对多设计变量和多源不确定性的特征,本文以确信可靠性理论为基础,提出直接面向市场需求的确信可靠性正向设计优化方法,以解决系统性设计优化与不确定性量化分析的问题。确信可靠性理论是一种新的可靠性理论[12],其基于裕量可靠、退化永恒和不确定性原理,从性能裕量的角度构建起产品性能与可靠性之间的相关关系[13],并通过综合度量工程中的固有不确定和认知不确定因素[14],实现产品定量建模与定量设计[15],更适合面向用户需求的产品可靠性正向设计优化过程。
综上,本文基于确信可靠性理论,以性能裕量为核心,研究新型扭簧电连接器的确信可靠性正向设计优化方法,以解决新型电连接器设计中的多维设计变量和多源不确定性问题。
1 基于确信可靠性的正向设计优化流程
1.1 确信可靠性理论
确信可靠性理论以裕量可靠、退化永恒及不确定性3 方面可靠性科学原理为指导,构建了基于学科方程、裕量方程、退化方程和度量方程的理论体系[12],具体表示为[12,16]

在这些方程中,核心是产品性能P、裕量M、可靠度R,相关影响因素包括内因变量X、外因变量Y、可逆时间t、不可逆时间→t[17]及性能阈值Pth,它们之间的关系由距离函数d(·)、退化函数f→t(·)和测度函数μ(·)量化。 另外,学科方程中f0表示未发生退化时产品性能与内外因变量及可逆时间的函数,M~表示受不确定性影响的性能裕量。
在确信可靠性理论框架下,产品性能裕量M决定了产品的可靠程度,可靠度就是对性能裕量大于0 的度量。 要在产品正向设计过程中达到高可靠度,核心即围绕性能裕量建立4 个方程。
1.2 基本流程
在实际正向设计中,最首要的任务是保证初始状态下产品裕量可靠,否则考虑产品的退化也没有意义。 因此,本文确信可靠性正向设计优化的根本目标是在功能需求Pth要求下,以关键性能P的裕量M为核心,考虑外因变量Y的影响,通过优化内因变量X的设计值使产品更可靠。 为此,本文基于初始状态提出了确信可靠性正向设计优化的基本流程,如图1 所示。
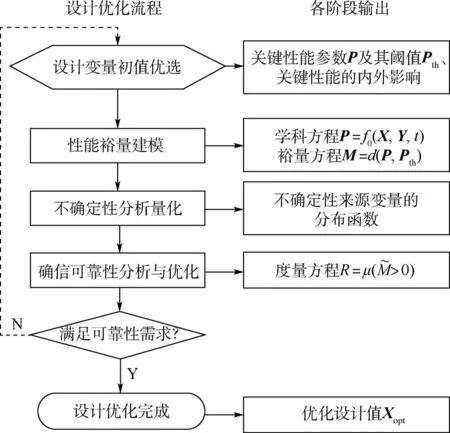
图1 确信可靠性正向设计优化流程Fig.1 Process of function oriented belief reliability design and optimization
1) 设计变量初值优选。 分析产品功能原理和确定关键性能,识别系统内外影响因素,并通过设计正交实验初步确定使得性能最优的设计变量组合作为设计初值。
2) 性能裕量建模,即构建关键性能的学科方程和裕量方程。 主要有2 类方法:①基于产品功能性能关系进行理论推导,构建解析模型;②通过实验构建代理模型,通常可使用响应面方法。
3) 不确定性分析量化。 一方面,明确内外因素可能受到的不确定性影响,分析不确定性的来源;另一方面,确定不确定性因素的分布类别与分布函数,实现不确定性量化。
4) 确信可靠性分析与优化。 建立初始确信可靠性度量方程,并基于产品可靠性要求建立优化模型,求得使可靠度最大的设计值。
由于对产品认知和实验条件的限制,上述流程通常需要随着研发过程推进和实验能力提升不断迭代进行。 另外,除本文关注的初始确信可靠度要求外,还要在进一步的设计中关注产品的性能退化过程,从而实现产品的迭代优化与可靠性增长。
2 确信可靠性正向设计优化方法
本节将基于图1 中给出的确信可靠性正向设计优化流程,详细阐述针对新型扭簧电连接器的确信可靠性正向设计优化方法。
2.1 设计变量初值优选方法
在新产品正向设计之初往往要考虑大量影响因素,众多的设计变量与水平数让组合方案数量庞大。 为提高设计优化效率和节约设计成本,从众多的设计方案中选出性能最优的设计变量组合,本文将设计变量初值优选的过程分为3 个递进的关键步骤,即确定关键性能和阈值、内外影响因素分析和基于正交实验的设计变量优选。
2.1.1 确定关键性能和阈值
关键性能P是指产品使用者和设计者最关心的功能评价指标或指标体系,可基于FPMA 方法展开分析[13]。 新型扭簧电连接器的功能是在大功率传输和信息传递中保证电连接器的稳定导通和安全使用,其性能包括温升、接触电阻、插拔力、插拔寿命、电压降等。 在正向设计中,通常将温升ΔT确定为新型扭簧电连接器的关键性能,主要有2 方面原因:①新型扭簧电连接器往往需要在几十安培充电电流下可靠工作,通电后温升过高可能导致焊点或结构熔化,造成极大安全隐患[18];②温升是最直观、最易测量的性能指标,且可在一定程度上从侧面反映接触电阻、插拔力等其他性能的水平,具有更好的综合性。
阈值Pth是性能可满足要求的边界值,根据不同的要求分为规定阈值Pth,c、破坏阈值Pth,d等。规定阈值是由行业标准手册和用户需求规定的性能边界;破坏阈值是产品发生不可逆破坏或产生安全隐患的失效边界,由材料属性决定[15]。 对于扭簧电连接器而言,规定阈值通常不能覆盖全部的工作场景。 例如,电动车行业标准SAE/USCar2中规定,连接端子通电后任意时刻的最大温升不得超过55 K[19],即ΔTth,c=55 K,但却未考虑使用环境温度。 因为焊锡在熔点(183℃)90%的温度下(即Tmax=164.7℃)就将发生松脱,所以不同环境温度Te下均对应着不同的温升破坏阈值ΔTth,d。 由于温升越小越好,取各类阈值中的最小值作为温升阈值:

2.1.2 内外影响因素分析
内外影响因素是指影响关键性能的产品内部因素(结构、材料、工艺等)和外部因素(工作应力、使用环境等)。 为了基于确信可靠性进行新型扭簧电连接器正向设计,必须明确内外影响因素,为裕量建模奠定基础。 本文通过分析温升产生的机理来确定内外影响因素。
温升的机理可从产热和散热两大方面考虑。产热方面,由焦耳定律Q=I2Reqt可知,工作电流大小和接触电阻大小都对温升有决定性影响。 工作电流作为环境载荷通常由实际使用情况而定,而体电阻、收缩电阻及膜层电阻3 部分组成的接触电阻由产品设计决定。 其中,体电阻与端子材料、结构有关,收缩电阻、膜层电阻则与插拔过程的过盈量与端子磨损程度相关。 散热方面,材料与环境的热量交互会影响温升。 当扭簧电连接器温度高于环境温度时,就会通过热传导、热辐射和热对流的方式向环境散热,因此由材料热特性决定[20]。
本文使用向量X= (x1,x2,…,xn)T和Y=(y1,y2,…,yr)T分别表示内外因变量,其中n和r分别表示内外因变量个数。 具体而言,内因向量X需要进行设计以使产品获得最优性能,因此也称为设计变量,其既包括离散变化的离散型变量XD,也包括在一定区间范围内连续变化的连续型变量XC。 例如,板材厚度只能从供应商提供的某几个类型中选择,是离散型变量;扭簧的扭转角度可以在(0°,90°)间选取,是连续型变量。 新型扭簧电连接器端子的外因向量Y主要涉及电流Ii和环境温度Te。 其中,Ii,i∈V表示不同工作场景i下的电流,V表示工作场景集合,Te表示扭簧电连接器外环境温度。
2.1.3 基于正交实验的设计变量优选
根据上述分析,新型扭簧电连接器端子的设计变量初值优选需要实现2 方面目标:针对离散型设计量XD,从有限的取值可能中确定使得温升最低的取值组合XD,0;针对连续型设计变量XC,探索其对温升性能的影响,初步选出最优水平组合XC,0作为设计优化的初值。
为了实现上述目标,本文使用正交实验设计方法[21]实现新型扭簧电连接器端子的多维离散-连续设计变量初值优选,并初步确定各设计变量及其相互作用对温升的影响和程度[22]。
首先,要确定所有内因变量的水平。 若第k个变量有Jk个水平,则记xkj为其第j个水平对应的变量取值,其中k=1,2,…,n,j=1,2,…,Jk。随后,根据变量个数及水平数选择合适的正交表进行实验。 最后,通过主效应和交互作用分析每个内因变量及其各个水平xkj对温升的影响并选出在现有水平下内因变量初值的最优组合X0=(XD,0,XC,0)T= (x1,0,x2,0,…,xn,0)T。
2.2 性能裕量建模方法
新型扭簧电连接器温升的学科方程难以求得解析表达式,在构建其性能裕量模型时往往需采用响应面方法求解多变量-响应问题,建立温升性能与多种变量间的关系,即学科方程的代理模型。
2.2.1 学科方程的构建
响应面法的核心原理是将变量与响应间的关系视为响应曲面[23],通过选取采样点设计有限的实验得到响应面上采样点的响应,加权回归后用多项式代理模型拟合响应目标和变量之间的变化关系[24]。 因此,对于新型扭簧电连接器端子而言,其学科方程的构建主要包括如下步骤:
步骤1 确定所有变量取值范围,由于离散型内因变量选型已确定,设计响应面所考虑的变量Θ应包括连续型内因变量XC和外因变量Y,即


式中:a0为常数项;矩阵A= R1×(m+r)为一次项系数;矩阵B=R(m+r)×(m+r)为二次项系数;ε为随机扰动项。 随着项数增加,拟合的方程通常更精确,但计算过程更加复杂,且并非所有项都会对结果产生决定性影响,容易因项数过多产生过拟合问题,因此,本文用方差齐性检验(F-test)检验式(11)中各项的显著性,过滤出显著项[22-23],并得到简化的学科方程:

2.3 不确定性分析与量化方法
为了分析新型扭簧电连接器端子在不同内外因变量作用下的确信可靠性水平,还需针对其裕量方程开展不确定性分析与量化。
裕量方程的不确定性主要来源于3 个方面:模型形式及系数的不确定性、内外因变量的不确定性以及性能阈值的不确定性。
模型的不确定性是代理模型构建过程中引入的,这使得模型预测值与实际值存在一定偏差,因此本文在学科方程中加入随机扰动项ε,其分布为Φε。
内外因变量的不确定性源于生产制造的尺寸偏差和外部环境的变化与波动。 对裕量方程中的内因变量X★,要综合考虑制造公差、设备精度和测量精度的影响,往往可以通过收集生产制造的相关数据给出其分布,表示为Φx1,Φx2,…,Φxm1。对于外因变量Y★,通常可假定电流和环境温度服从正态分布ΦI、ΦTe,即Ii~N(μIi,σIi),Te~N(μTe,σTe), 其中,i∈V表示工作场景,电流均值是对应场景下的额定电流值,环境温度均值为规定的工作环境温度。 根据3σ原则,分别取其波动范围的1/3 为标准差,即σI=εI/3,σTe=εTe/3。
性能阈值的不确定性由工作场景的变化和波动导致。 因为温升的阈值本质上是工作环境温度的函数,可以据此计算阈值的分布ΦΔTth。
2.4 确信可靠性分析与优化方法
基于上述确定性模型与不确定性量化结果,新型扭簧电连接器端子的确信可靠度即为性能裕量大于0 的概率,即
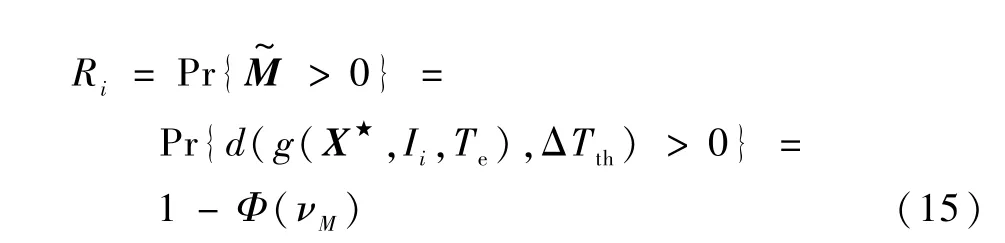
式中:Ri为工作场景i下扭簧电连接器端子的确信可靠度;νM= -μM/σM,μM和σM分别为裕量的均值和标准差。 当裕量分布形式简单时,可直接用式(15)求解,否则可用蒙特卡罗仿真。
为得到最优设计值,本文以最大化任意规定工作环境下确信可靠度为目标,以核心内因变量X★的均值μX★= (μx1,μx2,…,μxm1)为决策变量,以成本和设计变量取值范围为约束建立优化模型(16)。 其中成本由加工精度、工艺、仪器设备等多项因素共同决定,可认为是设计变量目标值与标准差的函数。
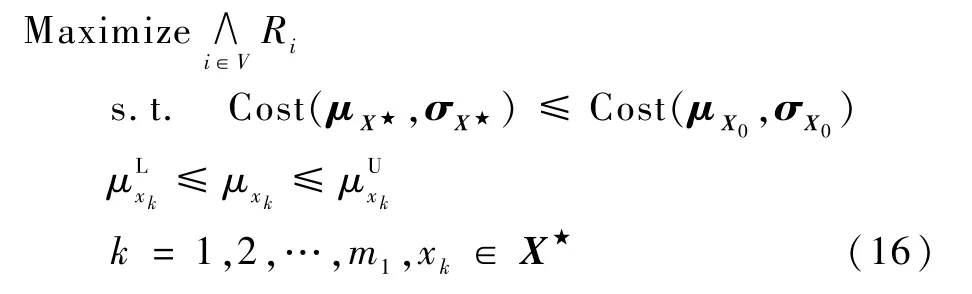
3 案例研究
本文以某新型3.6 mm 扭簧电连接器的正向设计过程为例,说明本文方法的有效性。
扭簧电连接器的研发目的是设计高可靠的电连接器通用标准件,以满足电动车电连接器的使用需求。 在现阶段受到生产加工、实验能力等限制,主要优化目标是在新结构、小尺寸、多设计变量和复杂工作环境下,提高初始确信可靠度。
3.1 设计变量初值优选
首先,确定关键性能和阈值。 由于选择了温升作为关键性能,通过调研用户需求和电动车行业标准IEC 60320-1[24]、SAE/USCAR-2[19]、GB/T 20234.1—2015[25]等,可以获取扭簧电连接器的工作场景集V和不同工作场景i∈V下的规定阈值ΔTth,c,如下:
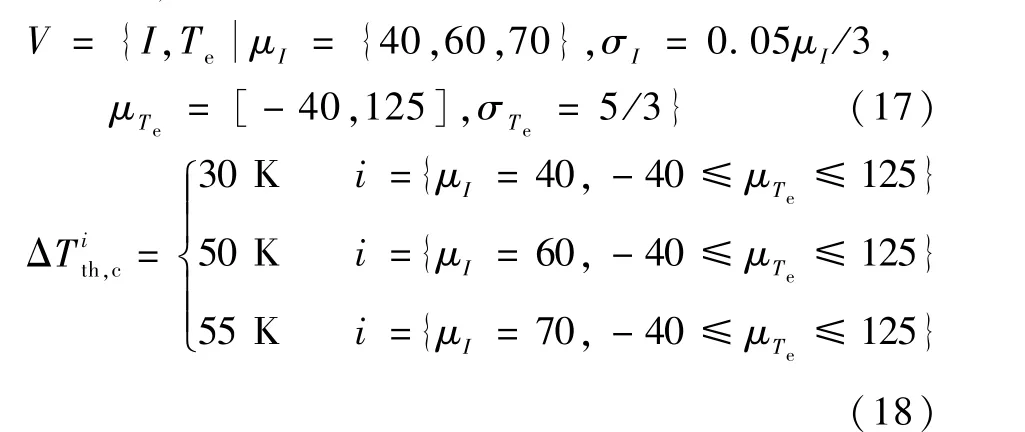
式中:i={I=70 A,Te∈[ -40,125]℃}的工作场景最常用。 之后可由式(5)得到温升阈值ΔTth。
其次,内外影响因素分析。 由于外部影响因素只需考虑电流和环境温度,在此主要对内部影响因素进行分析,得到各变量的类型、备选水平数和用以开展实验的各水平具体取值。
对于离散型变量,按照实际生产制造等条件将可选水平一一列出。 例如,扭簧材料共有C17410、C17510、QBe2. 0 共3 种可供选择,因此扭簧材料的水平数为3。 对于连续型变量,则根据设计需求在变量取值范围内确定水平。 例如,扭簧的扭转角度可以在(0°,90°)间选取,而根据产品设计初期的经验和工艺条件,本文给出了45°、50°及55°这3 个水平。 为能更清晰地了解新型扭簧电连接器的正向设计中有哪些设计变量,水平如何选取,本文将13 个影响因素及其水平选择均展示在表1 中。
表1 中,内因变量X共13 个,7 个是离散型变量,6 个是连续型变量,包括加工工艺、粗糙度、材料、扭转角等。 有2 个变量是2 水平,11 个变量是3 水平。 表中,D 表示离散型变量,C 表示连续型变量;孔套内径与扭簧材料厚度有关,孔套与扭簧直接配合,但二者需分开加工,将二者设计目标值分开考虑。
在此基础上,初步确定了扭簧电连接器的结构模型,如图2 所示。
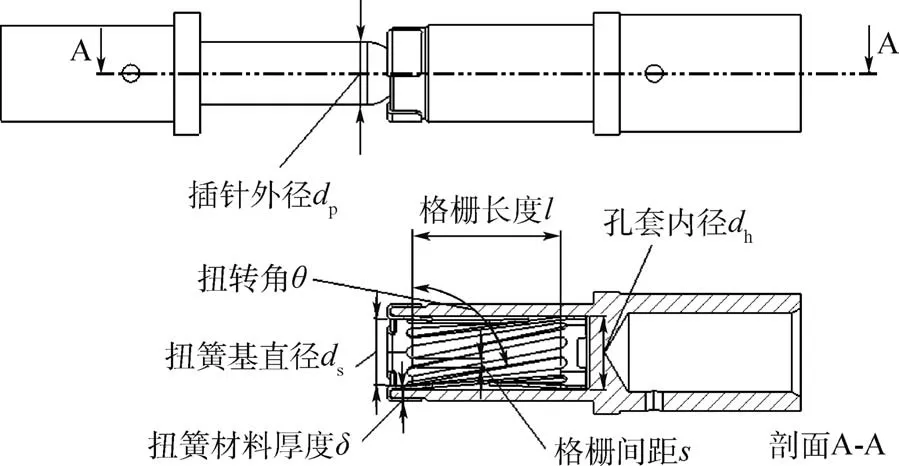
图2 结构参数Fig.2 Structural parameters
然后,基于正交实验的设计变量优选。 根据表1 分析的各变量水平取值,本文用有限元方法开展正交实验。 在温升仿真过程中,由于镀层和粗糙度水平的变化影响小,可暂时视为常量,用摩擦因数、热辐射率等材料参数等效。 选择混合正交表L36(39×22)对其余11 个变量的取值组合进行仿真。 基于效应分析评估各内因变量的主效应和交互作用,图3 为正交实验数据结果的可视化展示。

表1 内因变量分析Table 1 Analysis of endogenous variables
由图3(a)主效应图可以看出单变量对温升的影响。 点越靠近下方代表在相应水平作用下的温升越低。 以扭转角为例,可以看出,温升与角度成明显的负相关。 而图3(b)交互作用图反映变量间的耦合影响,折线的交叉反映变量间有交互作用,平行则代表变量间独立。 例如,格栅长度和插针材料间交互作用明显。
要开展初值优选,还需考虑3 方面问题。①由于交互作用的存在,最优水平组合可能与主效应最优水平集不一致。 例如,扭簧材料选择C17410,扭簧材料厚度选择0.25 mm 时各自的主效应最优,但当扭簧材料选择C17410 时,扭簧材料厚度选择0.2 mm 时的组合效果最佳。 ②用户需求发生变更,或者生产加工条件受限,所选水平无法作为设计值。 例如,在原有加工工艺水平下工艺A 更成熟,但用户要求采用新工艺B。 ③水平选取的范围过于保守或过于粗放,实际最优值落在水平范围外或某两水平之间。 例如,图3(a)主效应图显示扭转角与温升基本呈线性关系,这说明55°的设计值较为保守。 再如,孔套内径与扭簧材料厚度和扭簧基圆直径的选择相关,当二者取值确定后,孔套内径取值范围落在4. 15 ~4.25 mm之间,这说明之前的水平确定过于粗放。因此,本文结合工艺难度、成本、产品定位及用户需求等多项因素更新离散型变量选型和连续型变量设计范围。 例如,采用工艺B 的设计方案后尽量通过改进工艺提高加工精度,通过增大扭转角设计范围进一步寻找最优设计值。
分别对扭转角、插针外径、孔套内径的水平取值作出变更后,在更新的最优水平组合下,进行粗糙度和镀层的2 因素3 水平全数实验,发现采用Ra 为0.8 的设计粗糙度和金作为镀层材料组合性能最优。 基于图3 的结果给出的设计变量初步优选水平,并在用户需求等因素的限制下进行了额外的判断和相应的调整后,表2 给出了设计初值优选的输出结果。

图3 效应分析结果Fig.3 Results of effect analysis
3.2 性能裕量建模
基于表2 中的设计选型结果,离散型内因变量的选型可以直接确定,而各连续型内因变量和外因变量的最优设计值则需通过响应面法进一步确定,本文按表3 设计响应面采样点。
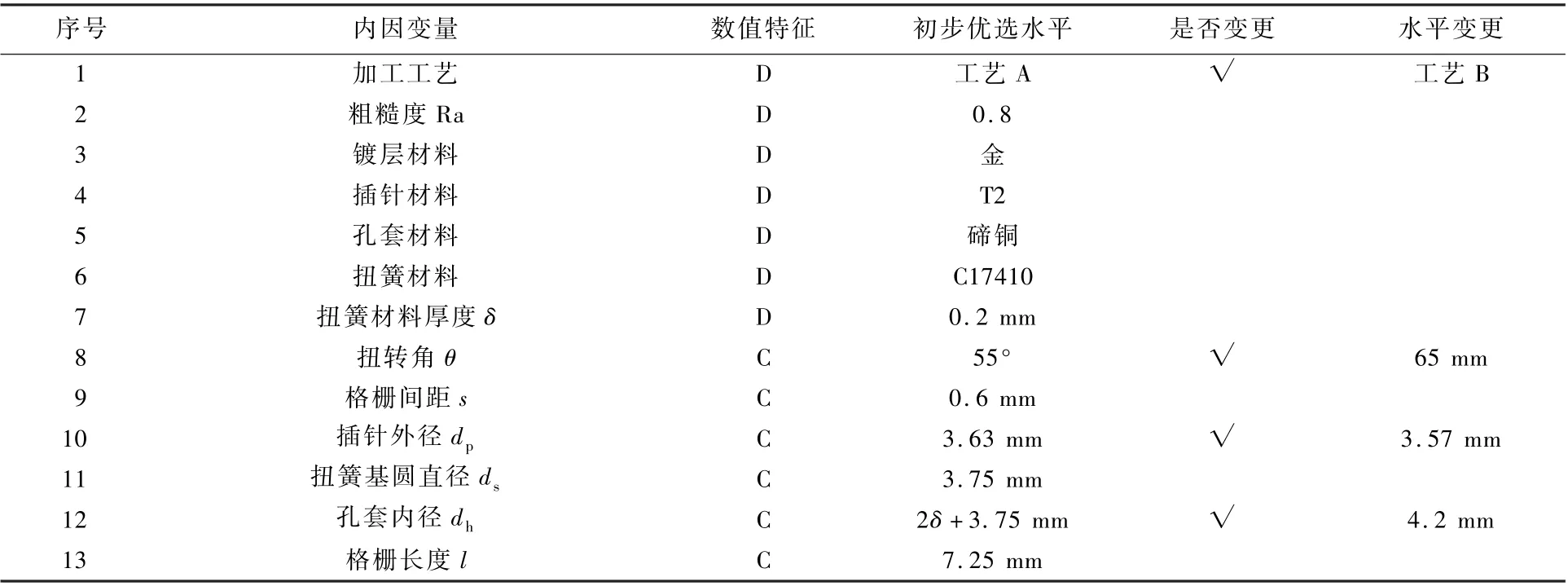
表2 确定最优设计变量初值Table 2 Determination of optimal initial values
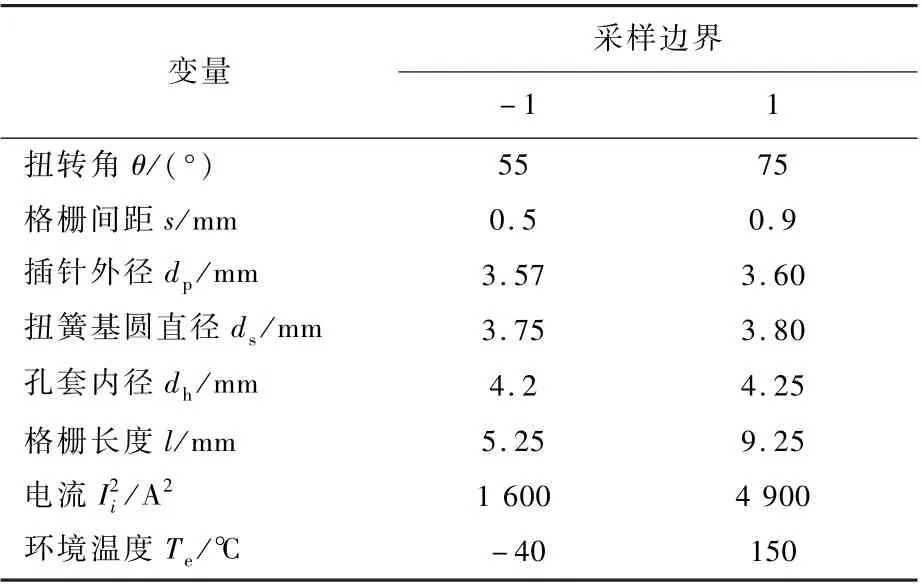
表3 响应面采样点Table 3 Sampling points of response surface
需要注意的是,在定义电流的采样边界时,以额定电流上下界的平方作为电流响应的采样边界,从而放大电流平方的响应。 定义环境温度采样边界时,虽然用户需求规定扭簧电连接器的工作环境温度大致在[ -40,125]℃之间,但扭簧电连接器在相对密闭的环境中温度会高于连接器表面温度,因此为使模型能更好覆盖实际工作剖面的环境温度,取响应面采样环境温度上边界为150℃。
用二阶模型拟合后,经方差齐性检验(F-test)在95%的置信水平下得到了仅含显著项的归一化代理模型,该模型F值为111.4,R2为0.854 1,有效信噪比为39.06,说明拟合效果较好。
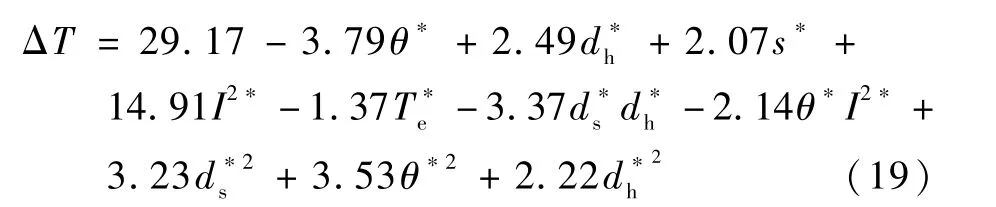
按各项的显著性排序,影响温升的核心变量依次为电流、扭转角、孔套内径、格栅间距、环境温度、扭簧基圆直径,即外因变量与核心设计变量为

3.3 不确定性分析与量化
由裕量方程可知,模型形式及系数不确定性、内外因变量的不确定性、性能阈值的不确定性同时存在,且有复杂的关联影响。
首先,模型形式及系数的不确定性分析量化。假设随机扰动ε服从标准正态分布,本文基于响应面实验结果,用式(22)算出了σ的无偏估计。其中,N为采样点总数,p为模型的显著项项数,e为响应面残差。
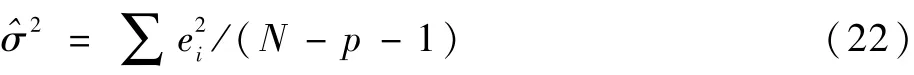
之后,内外因变量本身的不确定性分析量化。对于扭簧基圆直径、孔套内径、格栅间距这些加工精度较高的内因变量,认为它们服从以设计值为均值,加工/测量仪器精度为标准差的正态分布。而扭转角由于采用新工艺加工,且有一定的测量难度,本文采用均值已知标准差未知的样本假设,通过收集实测数据,求出了扭转角的极大似然估计,经皮尔逊卡方检验以及偏峰度检验,正态分布假设成立。 电流和环境温度这2 个外因变量则服从以额定工作条件为均值,波动范围为3σ的正态分布。
最后,性能阈值的不确定性分析量化。 温升阈值的期望和方差可根据阈值与电流、环境温度、工作场景的函数间接求解。
在上述分析与假设下,表4 给出了所有随机变量的正态分布参数。

表4 随机变量的分布Table 4 Distribution of random variables
3.4 确信可靠性分析与优化
基于上述分析,本文构建如下确信可靠性优化模型。 由于扭簧电连接器尺寸小,设计值变化范围小,用料对成本影响小,现阶段的成本主要由加工精度和工艺决定,优化模型也就转化为标准差不变的随机期望优化问题。

其中,期望的变化范围即设计变量的取值范围。 为了求解该模型,本文使用蒙特卡罗方法求解确信可靠度,以3.1 节中优选得到的设计方案为初值X0,用模拟退火的启发式方法求解设计变量最优取值Xopt。
表5 展示了使得初始确信可靠度最高的设计方案。 可见,扭簧基圆直径和扭转角的设计值对可靠度的影响存在拐点,最优值分别为3.773 mm和73.87°。 孔套内径和格栅间距的最优设计值则是各自设计范围的下界,即4.202 mm 和0.5 mm。由此可以进一步更新设计值,从而定量提高扭簧电连接器的可靠度。

表5 确信可靠度优化结果Table 5 Results of belief reliability optimization
进一步地,本文用蒙特卡罗方法分别计算了在3 种额定电流下,初值和优化值对应的温升、温升阈值。 图4 展示了优化前后温升-阈值对比结果。 其中,fΔT(x)为温升的概率密度函数, ΔTX=X0和ΔTX=Xopt分别表示初值和优化值下的温升,ΔTth为温升阈值。

图4 优化前后温升分布对比Fig.4 Comparison of distributions of temperature rise before and after optimization
在3 种工作场景中,温升随着额定电流的增大明显升高,I=70 A 是最严酷的工作条件。
可看出由于不确定性的作用,扭簧电连接器虽然在设计初值下能保持较低的温升,但仍存在较大的温升超过阈值的风险。 而基于上述优化模型得到的优化值,本质上是降低了温升的均值,从而增大了裕量,使产品更可靠。
为了更直观地展示裕量的优化效果,图5 对优化前后的裕量分布进行对比。 其中,fm(x)为性能裕量的概率密度函数,Fm(x)为性能裕量的累积分布函数。

图5 优化前后裕量分布对比Fig.5 Comparison of margin distribution before and after optimization
可见同初值相比,优化值下扭簧电连接器的裕量显著提高,尤其是最恶劣环境I=70 A 下优化效果最为明显,裕量分布的均值增大,标准差减小,仅有少数仿真结果中裕量小于0。 由此实现了在多种工作场景下,产品初始确信可靠度的定量提高。
4 结 论
本文依托工程案例系统性总结了新型扭簧电连接器的确信可靠性正向设计优化方法,将正向设计优化划分为周期迭代过程,每周期按照设计变量初值优选、性能裕量建模、不确定性分析量化、确信可靠性分析与优化4 个阶段依次展开,从而在确信可靠性理论框架下考虑多维离散-连续变量及其不确定性作用,实现新产品的正向优化设计。 主要贡献如下:
1) 面向新型扭簧电连接器的可靠性正向设计需求,提出了基于确信可靠性的系统化可靠性正向设计方法;
2) 综合考虑和量化了选材、工艺、手册标准、外界环境、工作条件等多源不确定性影响,构建了确信可靠性设计优化模型,实现了多维离散-连续设计变量下的设计方案优化;
3) 通过开展正向设计的实际案例研究,验证了设计变量优选、性能裕量建模、确信可靠性优化建模等方法的有效性,可为其他新产品的可靠性正向设计提供参考。
需要指出的是,在案例分析阶段,本文基于实际案例只进行了初始确信可靠度的正向设计优化。 因此,在未来研究中,还应根据设计需求开展考虑产品退化的可靠寿命优化设计方法研究。

