基于边界元法的三维结构体滑跳运动数值仿真
杨超 姜宇 吴志刚
(北京航空航天大学 航空科学与工程学院, 北京 100083)
水面滑跳是结构体近水面小角度斜撞水过程中发生的一种特殊运动,日常生活中在河边进行的“打水漂游戏” 就是一种典型的滑跳现象[1]。结构体在滑跳运动过程中,不断地以较大的水平速度和较小的垂向速度斜向撞击水面,损失一部分动能的同时,还会被水面弹起。 近年来,不断有学者提出利用这种滑跳运动来实现近水面高速机动飞行的新概念跨介质飞行器[2-5],也称为击水式飞行器。 因此,水面滑跳问题作为跨介质飞行器的基础问题也逐渐受到关注。
结构体近水面滑跳问题涉及复杂多相流动与结构体大幅运动的相互作用,尤其是结构体高速斜入水冲击过程中带来的受力剧烈变化。 目前,国内外对结构物高速斜入水冲击载荷问题的研究,主要集中在结构体垂向砰击水面带来的载荷,在工程应用领域具有一定的局限性。 例如,Zhao和Faltinsen[6]在1993 年针对二维楔形体的垂直入水进行了计算;樊征和刘莹莹[7]采用解析法分析了二维小升角楔形体的垂向入水问题;2008年,许国冬等[8]讨论了V 形楔多种入水形式的相似解;Faltinsen 和Chezhian[9]以非轴对称的船体模型入水为研究对象,基于Wagner 理论,研究了三维垂向入水砰击的数值方法。 也有部分研究考虑了结构体的弹性效应。 例如,1991 年,顾懋祥等[10]采用迭代法计算了平头旋转壳体垂直入水时的水弹性效应;Takagi[11]在1994 年运用Wagner 的平板近似理论计算了弹性结构的入水冲击问题;2017—2020 年,张岳青等[12-13]对楔形体和弧形体的垂直入水进行了试验和商用软件数值仿真;2018 年,Mohammad 和Maurizio[14]对柔性细长体的垂直入水冲击载荷进行了理论分析和试验验证;2004—2006 年,Wu 等[15-16]提出了二维楔形体的迭代求解方法,并运用二维边界元法,使用柯西积分计算了楔形体入水的相似解。 边界元法是基于边界积分方程,采用与有限元法[17]类似的分元、离散思想建立起来的。 由于边界积分方程是定义在边界上的,边界元法只要在边界上划分单元,相比于区域解法降低了维度,具备较高的计算效率和计算精度[18]。 相对而言,结构体高速斜入水冲击问题的研究较少。 2008 年,王永虎、石秀华等[19]以入水冲击的理论动力学和入水弹道学理论为基础,完成了鱼雷头部尖拱的斜入水高速冲击载荷的分析;2009 年,陈占晖和卢永锦[20]利用流固耦合有限元法研究了立方体斜向冲击水面的运动特性;2012 年,郑金伟和宗智[21]利用LSDYNA 软件计算了三维刚性椭圆头结构的高速斜入水冲击载荷;2014 年,Scolan[22]完成了三维不规则外形的刚体结构低速斜入水冲击载荷试验;2021 年,蔡维轩等[23]完成了无旋圆盘的滑跳运动试验;同年,王聪等[24]对旋转圆盘的滑跳特性进行了理论仿真。 可以看出,考虑结构弹性效应影响的三维结构体高速斜入水冲击载荷数值求解算法的研究较少。
为了高效求解三维结构体滑跳运动问题,本文基于边界元法,建立了一种可以考虑弹性效应的三维结构体近水面滑跳运动的时域数值仿真方法。 在三维结构体的滑跳运动过程中,高速斜入水冲击载荷由边界元法求得,利用状态方程直接积分法(direct integration of state equation method)求解得到结构节点位移动力响应,并通过滑跳运动动力学模型更新结构体的质心位置及运动速度。 这使得本文方法既可以应用于三维弹性结构体,也拥有较高的计算效率。 针对刚球高速斜入水冲击现象进行了数值仿真,并与试验值进行了对比,验证了该方法流体载荷求解部分的准确性。针对三维球冠体的近水面滑跳运动进行了时域数值仿真,得到了对应的运动特性。 研究了不同的初始参数(结构质量、初始高度、水平抛出速度和半径大小)和结构弹性效应对球冠体近水面滑跳运动的影响,总结了相应的规律。
1 问题描述
本文分析的三维结构体近水面滑跳运动问题可以由图1 表示,半径为r0的球冠体结构在质心距离水面高度H0的位置上以速度V0水平抛出。图中采用了如下坐标系描述:流场坐标系O-xyz,原点固定在流场正中心的O点,x轴和y轴固定在与O点同一高度的水平面上,z轴垂直向上。 结构坐标系O′-x′y′z′,原点固定在球冠体的质心O′点,x′轴和y′轴固定在与O′点同一高度的水平面上,z′轴垂直向上。 图1 中,Ω为流体域,S为流体域边界。

图1 球冠体近水面滑跳运动问题示意图Fig.1 Schematic diagram of near-water-surface skipping motion of hemispherical structure
2 理论方法
三维结构体高速斜入水冲击是流体和结构相互作用的强非线性过程。 在很多情况下,流体运动的速度比声速小得多,因此,除平头物体垂直入水外,一般可以忽略流体的可压缩性[25]。 入水冲击载荷具有瞬态极大值的特点,与之相比,入水冲击时流体的重力因素所造成的影响较小,因此作为简化条件,忽略流体重力的影响。
本文建立的基于边界元法的三维弹性结构体近水面滑跳运动时域迭代仿真方法的基本原理如图2 所示。 三维弹性结构体在近水面滑跳过程中受到斜入水冲击载荷、摩擦阻力、重力和浮力的共同作用,每个时间步内流场作用在三维结构体上的斜入水冲击载荷由边界元法求解得到,利用状态方程直接积分法求解得到结构节点位移动力响应。 流场载荷连同重力和浮力代入到滑跳运动动力学模型中进行分析,得到结构体新的质心位置及运动速度。 重新构造流场的形状和边界条件,并进入下一步迭代计算。
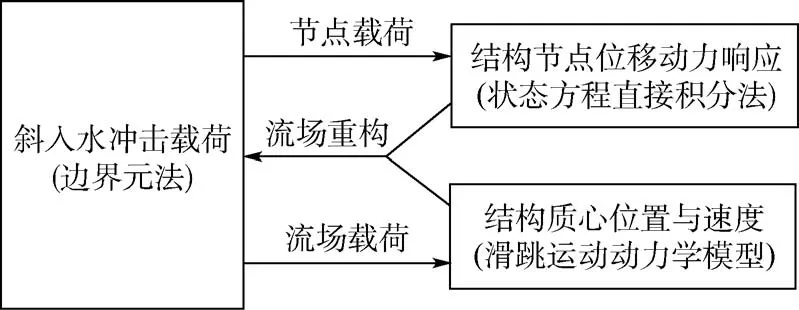
图2 时域迭代求解方法基本原理Fig.2 Basic principle of time domain iterative solution method
2.1 边界元法
根据流体区域的简化和假设,流体为无旋、无黏、不可压流体,则三维流体运动的速度势φ满足如下Laplace 方程:
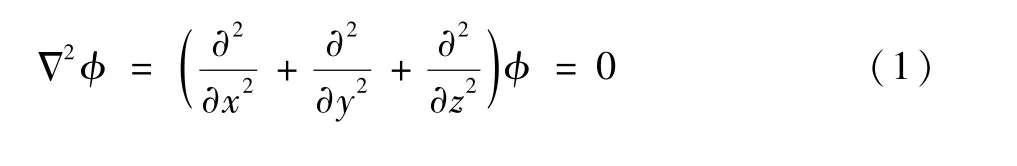
为了确定方程(1)在空间某个内部域或外部域的解,还必须附加定解条件,即边界条件。 对于本文分析的问题,满足Laplace 方程的第三边界条件,即混合条件。 流体区域自由表面上的边界条件为

对于三维Laplace 方程,其基本解φ*应满足条件[15]:

若以φ为所求三维Laplace 方程边值问题的解,而φ*作为辅助解ψ代入Green 第二公式(由Gauss 公式推得):

式(9)中的积分是对dS(q)积分,即在边界面对场点进行积分,q代表边界面上的场点。
为了建立边界积分方程,只需将基本解的域内源点P从流体域内趋向于边界面源点p,于是得到
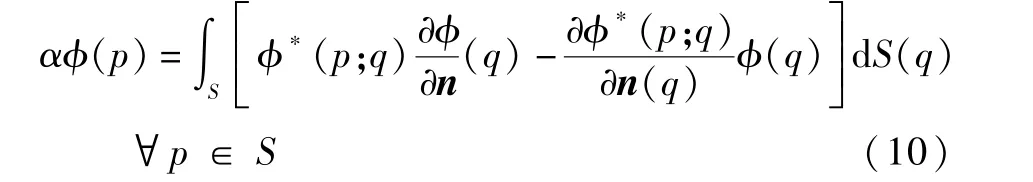
式中:α为边界面上源点p处的立体角系数。
对于本文分析的三维结构体,进行常值三角形单元的边界划分,如图3 所示。 对于常值三角形单元来说,相邻单元间未知量本身都不连续。在每个边界元上φ和∂φ/∂n都是常量,并用该边界元中点的值来代替。

图3 常值三角形单元Fig.3 Constant triangular element
p点取遍所有边界单元的中点,就可以得到如下矩阵:

式中:H和G分别为φ和∂φ/∂n的积分系数矩阵,仅仅与求解域的几何特性有关。
通过求解式(11),就可以得到三维结构体的入水过程中任意边界元中点的速度势。 在求得边界单元中点处的势函数值后,可以用一种简便的数值微分方法[26-27]计算浸湿表面上速度分布。设浸湿表面方程为y=y(x,z),势函数在浸湿表面上的增量可以写成

式中:u、v、w分别为边界元中点速度的3 个分量;l、m、k分别为边界元中点单位法向量的3 个分量。
图4 中,qi为控制点,Vi为控制点速度向量,Γ为控制点单位法向量,i和j分别为x坐标方向和z坐标方向的单位向量。
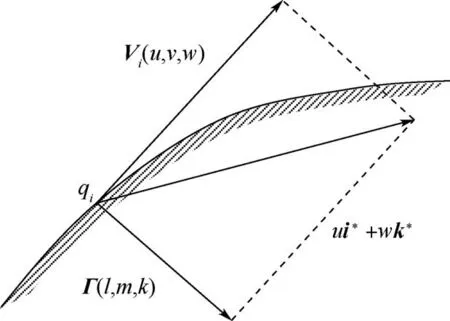
图4 速度分量求解示意图Fig.4 Schematic diagram of velocity component solution
在计算得到每个边界单元中心点的速度和速度势后,就可以利用下述改进的非线性伯努利方程求得每个边界单元对应的水动力压强[28]:

式中:pi为边界单元的压强;ρ为流体密度。
最后,每个边界单元的压强乘以每个边界单元的面积,即可得到每个边界单元对结构体的作用力。
2.2 高速斜入水冲击载荷模型
由于浸没在水中的体积排挤流体产生液面隆起现象[29],又称Wagner 型入水冲击,如图5 所示。 取决于入水结构体的外形和入水角等初始状态,下面给出确定液面隆起等效位置He的表达式,即

式中:θ为入水倾角;t为时间;η(x,y,z,θ,t)为函数表达式。 参考文献[30],圆球体倾斜入水时,He的取值固定为1.35 倍的初始液面入水深度。考虑自由液面的隆起现象后,会导致结构体浸湿表面扩大,高速斜入水冲击载荷增大。
结构体高速斜入水冲击载荷可以分为较大的水平速度带来的划水力和较小的垂向速度带来的垂向入水砰击载荷2 部分。 当结构体高速斜入水时,流体被排开,因此球冠体被浸湿的表面只有与速度矢量V夹角小于90°且低于液面隆起等效位置He的部分[31-32],示意图如图5 所示。 同样,只有这部分浸湿表面会受到高速斜入水冲击载荷。

图5 浸湿表面示意图Fig.5 Schematic diagram of water soaked surface
对于结构体浸湿表面的三角形常值单元,计算高速斜入水冲击载荷时的边界条件为结构体水平运动速度Vx的法向分量、垂向运动速度Vz的法向分量与结构体旋转角速度ω带来的速度Vω的法向分量之和,示意图如图6 所示。
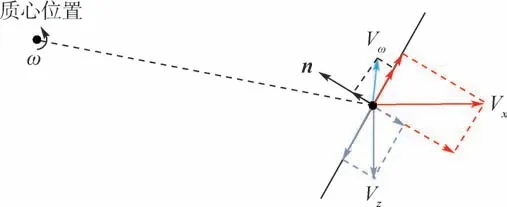
图6 斜入水冲击载荷模型单元边界条件Fig.6 Element boundary conditions of oblique water impact load model
当使用边界元法计算斜入水冲击载荷时,假设流体为理想流体。 而实际流体是有黏性的,因此在斜入水冲击载荷模型中,结构体与流体相接触的表面受到摩擦阻力的作用。 摩擦阻力系数cf可以直接选用帕兰特-许立汀紊流摩阻计算公式[3,33],即

式中:Re为雷诺数。
对于球冠体来说,结构底部较为平顺,因此流体黏性带来的摩擦阻力主要作用于水平方向,后续的分析中忽略垂直方向的摩擦阻力。
2.3 结构动力响应分析
本文采用状态方程直接积分法计算每个时间步内,弹性结构在流场载荷下的弹性动力响应[34]。 结构体在模态向量坐标下的动力平衡方程[35-36]可以表示为

式中:
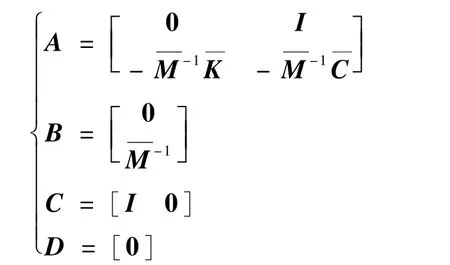
当有限元模型节点处所受的外力矩阵确定时,就可以通过状态方程直接积分法计算得到三维弹性结构体的位移响应[37]。
2.4 滑跳运动动力学模型
进行滑跳运动的结构体一般为对称结构,因此只需要考虑结构体的纵向平面内运动:水平运动、垂直运动和俯仰运动。 通过动量定理和动量矩定理[38],可以建立滑跳运动的全空间运动方程组。
当结构体在空中飞行时,没有流体载荷的作用,水平方向的运动方程为

式中:Flzi为浸湿表面单元高速斜入水冲击载荷的升力分量;Ffz为摩擦阻力的垂直方向分量。
俯仰方向上的运动方程为
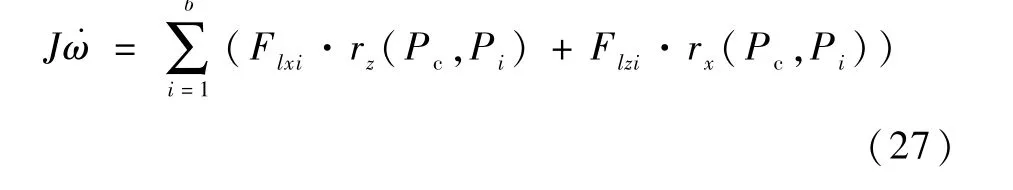
式中:Pc为结构体质心位置;Pi为浸湿表面单元中点位置;rx(Pc,Pi) 为结构体质心与浸湿表面单元中点x坐标的差值;rz(Pc,Pi) 为结构体质心与浸湿表面单元中点z坐标的差值。
2.5 时域迭代求解方法
本文建立的基于边界元法的三维结构体近水面滑跳运动时域迭代仿真方法流程如图7 所示。首先,进行分析模型的初始化和分析参数的设置,开始时域迭代计算。 在每一个时间步内,对结构体是否触水进行判断。 如果触水,由该时刻下的结构体表面和初始流场进行组合构造,确定该时间步的流场形状及流场边界条件,并提交边界元法程序进行求解,得到该时间步内流场对结构体的高速斜入水冲击载荷。 然后,将流场载荷插值到结构浸湿表面节点,并利用状态方程直接积分法得到结构节点的弹性位移动力响应。 如果结构体没有触水,则该时间步内流场对结构体的高速斜入水冲击载荷为0。 最后,根据滑跳运动动力学模型,更新结构体的位置与速度信息,并进入下一步迭代计算。
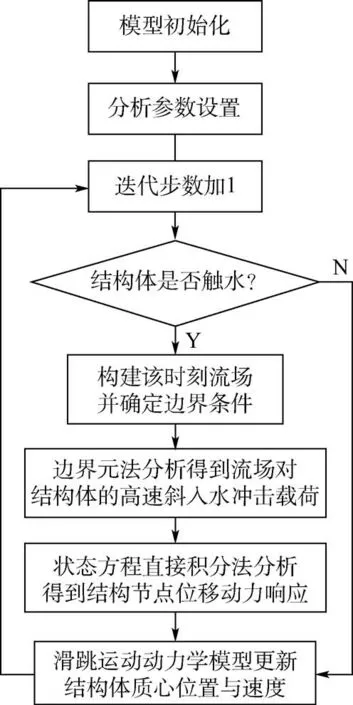
图7 时域迭代求解方法流程Fig.7 Flow chart of time domain iterative solution method
3 仿真计算及分析
3.1 数值方法验证
1976 年,为了研究高速斜入水冲击载荷的数值,Soliman 等[39]完成了钢球高速斜入水冲击试验,得到了一系列相关数据。
在Soliman 的试验中,高速斜入水冲击结构为钢制实心球体,直径为25.4 mm,入水速度大小为64.62 m/s。 试验使用安装在铸铁平台上的弹药枪,将炮弹射入装满水的有机玻璃水箱(6 ft长、1 ft 宽、1 ft 深,1 ft(英尺) =0.304 8 m)。 相关参数采用35 mm 摄像机及频闪仪进行测量。试验的示意图如图8 所示。 图中的钢球以入水速度V、入水倾角θ高速冲击水面,c代表钢球质心。

图8 钢球高速斜入水试验示意图Fig.8 Schematic diagram of high speed oblique water entry test of steel sphere
为了验证本文提出的三维结构体高速斜入水冲击载荷时域迭代求解方法的可行性和准确性,针对Soliman 的试验进行了数值仿真。 钢球具有较大的水平运动速度及较小的垂向运动速度。 数值计算结果与试验值的对比如图9 和图10所示。 其中,钢球离开水面时运动速度的数值计算结果与试验值对比如图9 所示;钢球离开水面时出水倾角的数值计算结果与试验值对比如图10 所示。
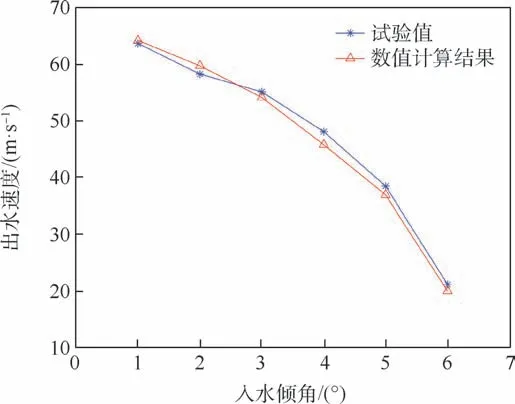
图9 离开水面速度数值计算结果与试验值对比Fig.9 Comparison between calculated and experimental values of velocity leaving water surface
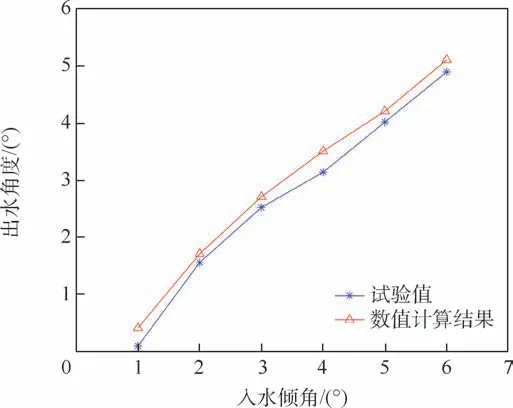
图10 离开水面倾角数值计算结果与试验值对比Fig.10 Comparison between calculated and experimental values of dip angle leaving water surface
通过图9 和图10 可知,当钢球入水倾角θ增大时,钢球在触水滑跳过程中的动能衰减增大,其离开水面时的速度倾角增大。 此外还可以看出,本文方法的数值计算结果与试验数值吻合良好,验证了本文提出的三维结构体高速斜入水冲击载荷时域迭代求解方法的可行性和准确性。
3.2 仿真建模
在本文方法中,每一个时间步都需要用到结构体的浸湿表面和未受扰动的流场来对下一个时间步的流场进行重构,结构动力响应分析也需要将结构体的模态分析结果作为原始数据。 因此,需要提前对结构体进行有限元建模和模态分析,建立未受扰动的流场,设置初始参数。
为了方便构成流场边界,需要预先对球冠体进行网格划分,即有限元建模。 球冠体半径为0.152 4 m,材料密度为1 800 kg/m3,质量为1.554 kg。 在结构有限元建模时,球冠体表面均采用三角形单元进行网格划分,构建完成的结构有限元模型如图11 所示。 材料的弹性模量为70 GPa,剪切模量为26 GPa,泊松比为0. 33。通过实心球冠体的模态分析可以得到,一阶固有频率高达3 800 Hz,球冠体的弹性效应很小。 因此,实心球冠体可近似地看作一个刚性物体。

图11 球冠体有限元模型Fig.11 Finite element model of spherical crown
针对直径为0.304 8 m 的球冠体结构,建立一个边长为1.0 m 的立方体流场,初始未受扰动的流场如图12 所示。 由于采用边界元法进行高速斜入水冲击载荷分析,流场内部没有网格划分,只是在边界表面上划分了共10 682 个三角形单元。 在滑跳运动计算过程中,流场随结构体质心的水平运动进行平移,流场的坐标原点始终处于质心的正下方。
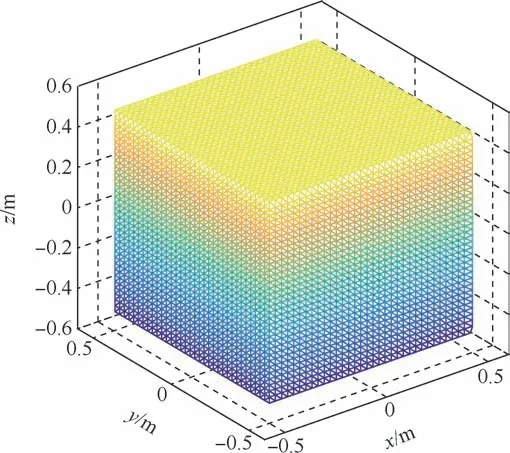
图12 初始未受扰动的流场Fig.12 Initial undisturbed flow field
对于标准算例,球冠体在距离水平面1.0 m的高度处,以25.0 m/s 的速度被水平抛出。 时域仿真总时长为1.4 s,迭代步长为0.4 ms,液体的密度设置为1 000 kg/m3,重力加速度g为9.8 m/s2。从第一个时间步开始,每个时间步的流场域上表面都是由流场的自由表面和结构浸湿表面重构而成。
3.3 刚性球冠体滑跳运动仿真
根据3.2 节的标准算例参数设置,应用本文建立的数值仿真方法对刚性球冠体进行近水面滑跳运动时域仿真,仿真总时长为1.4 s,仿真结果如图13 ~图19 所示。 其中,图13 为球冠体近水面滑跳运动的轨迹仿真结果,图14 为球冠体近水面滑跳运动的垂向速度时历曲线,图16 为球冠体近水面滑跳运动的水平速度时历曲线。
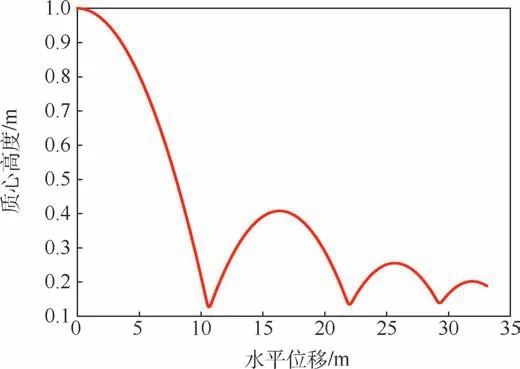
图13 滑跳运动轨迹仿真结果Fig.13 Simulation results of skipping motion trajectory
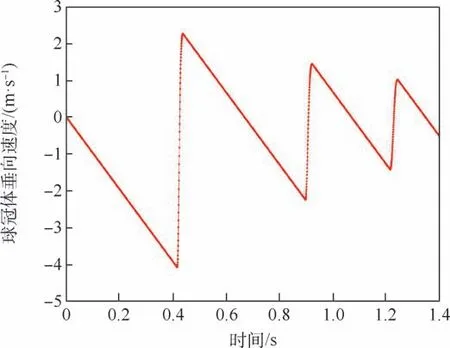
图14 滑跳运动垂向速度时历曲线Fig.14 Vertical velocity time history curve of skipping motion
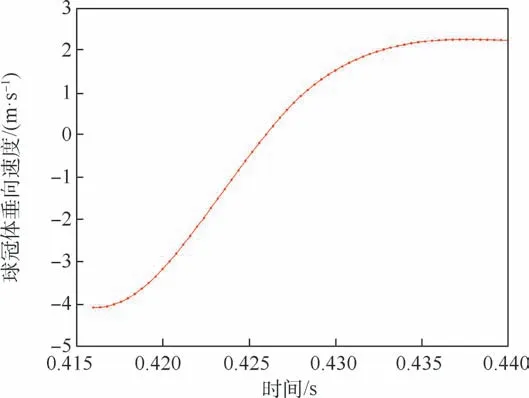
图15 第1 次触水垂向速度时历曲线Fig.15 Vertical velocity time history curve in the first contact with water

图16 滑跳运动水平速度时历曲线Fig.16 Horizontal velocity time history curve of skipping motion
根据图13 可知,本文建立的基于边界元法的三维结构体近水面滑跳运动时域数值仿真方法适用于球冠体近水面滑跳运动的数值仿真。 球冠体在1.4 s 内经历了3 次触水滑跳运动,每次触水弹起的质心最高位置逐渐降低。 此外还可以看出,第1 次触水滑跳过程时长约24 ms,入水深度为0. 025 m;第2 次触水滑跳过程时长约为28 ms,入水深度为0. 018 m;第3 次触水滑跳过程时长约32 ms,入水深度为0. 014 m。 可以看出,随着触水滑跳次数的增加,触水滑跳过程的时长增加,但入水深度减小。 通过图14 和图16 可知,球冠体在结构未触水的时间段内只受到重力作用,下降速度匀速增大,水平速度不变;当球冠体触水时,受到流场力的作用,在极短的时间内垂向速度由负转正,水平速度减小。 此外还可以看出,球冠体每次触水弹起后,垂向速度的最大值都会发生衰减。 垂向速度最大值和水平速度的减小,代表了球冠体动能在不断的触水滑跳过程中被消耗。 滑跳运动过程中结构体的水平速度不断下降,当触水弹起高度不足以使结构体脱离水面之后,滑跳运动结束。
由于球冠体每次触水滑跳时间过短,体现在图14 和图16 中,触水滑跳的垂向速度变化和水平速度变化近似折线形式。 而事实上,触水弹跳的过程中速度变化是连续的。 球冠体第1 次触水滑跳过程中的垂向速度变化曲线和水平速度变化曲线分别如图15 和图17 所示。 通过图15 可知,第1 次触水滑跳时间历程为0.416 ~0.44 s,时长为24 ms。 当球冠体刚接触水面时,垂向速度约为-4.0 m/s,受到流场力的作用,垂向速度迅速变化,约为0. 426 s 时由负转正,并继续增加至2.2 m/s离开水面。 通过图17 可知,水平速度由刚接触水面时的25 m/s 持续减小至23.5 m/s 离开水面,衰减率为6%(衰减率λ= (Vin-Vout)/Vin,其中Vin为球冠体第1 次触水之前的水平速度,Vout为球冠体第1 次触水之后的水平速度,下同)。
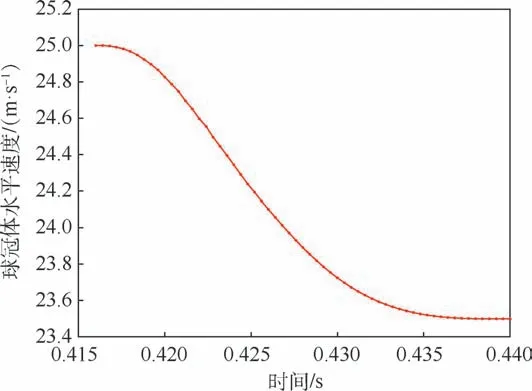
图17 第1 次触水水平速度时历曲线Fig.17 Horizontal velocity time history curve in the first contact with water
球冠体第1 次触水过程中的高速斜入水冲击载荷仿真结果如图18 和图19 所示。 其中,图18为球冠体在第1 次触水过程中的高速斜入水冲击载荷垂直方向分量时历图,图19 为球冠体在第1次触水过程中的高速斜入水冲击载荷水平方向分量时历图。
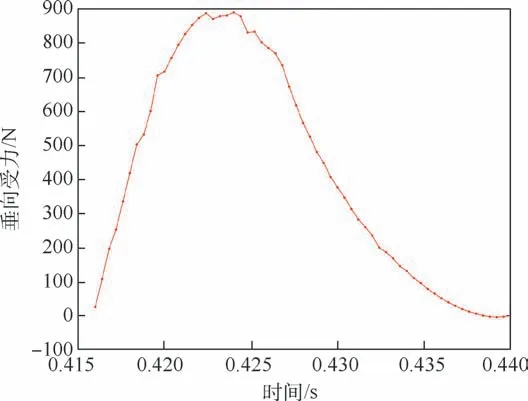
图18 第1 次触水垂向受力时历曲线Fig.18 Vertical stress time history curve in the first contact with water
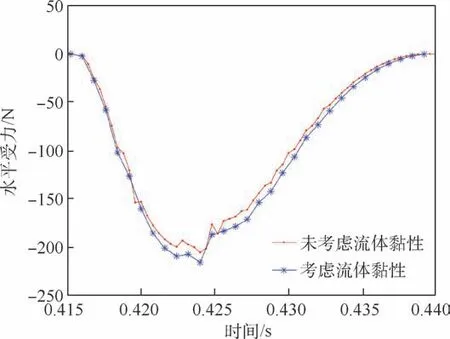
图19 第1 次触水水平受力时历曲线Fig.19 Horizontal stress time history curve in the first contact with water
通过图18 和图19 可以看出,在球冠体的第1 次触水过程中,高速斜入水冲击载荷提供了阻力和升力,都是很快达到峰值并逐渐减小。 分开来看,垂直方向受到的载荷方向向上,起到升力的作用,数值相对较大,在0. 422 s 时达到峰值887.2 N,在其作用下,球冠体下降速度迅速减为0 并加速上升,直至离开水面;水平方向持续受到阻力的作用,数值相对较小,0.422 s 时达到峰值-216.0 N,在其作用下水平运动速度不断减小。
对于球冠体而言,直径为0.304 8 m,第1 次触水滑跳时运动速度为25 m/s,流体密度为1 000 kg/m3。 经 过 计 算, 此 时 的 雷 诺 数 高 达7.5 ×106。 由图19 可知,在球冠体第1 次触水滑跳的过程中,考虑流体黏性的高速斜入水冲击载荷水平方向分量峰值为-216.0 N,未考虑流体黏性的高速斜入水冲击载荷水平方向分量峰值为-205.5 N,影响约为5. 1%。 由此可见,在高速斜入水冲击仿真过程中,流体黏性带来的影响较小,但是也不可忽略。 本文后续的仿真中,都已考虑流体黏性带来的摩擦阻力影响。
3.4 变参分析
3.4.1 结构质量对滑跳运动的影响
为了得到结构质量对球冠体滑跳运动的影响规律,在不改变其他分析参数的情况下,改变球冠体的密度,使得结构质量m0分别为1. 0,1.554,3.0 kg,仿真总时长为1.3 s。 不同结构质量的球冠体滑跳轨迹对比如图20 所示,不同结构质量的滑跳运动垂向速度时历对比如图21 所示,不同结构质量的滑跳运动水平速度时历对比如图22所示。
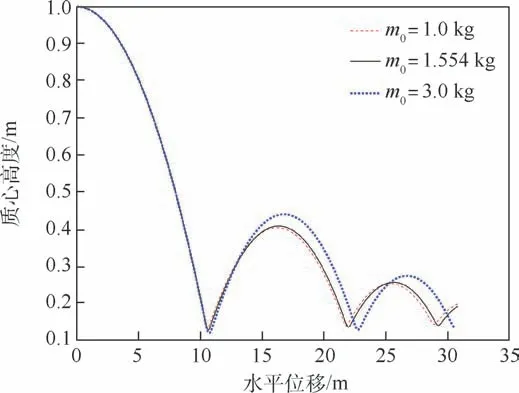
图20 不同结构质量的滑跳轨迹对比Fig.20 Comparison of skipping motion trajectory with different structural quality

图21 不同结构质量的滑跳垂向速度时历对比Fig.21 Time history comparison of skipping motionvertical velocity with different structural quality

图22 不同结构质量的滑跳水平速度时历对比Fig.22 Time history comparison of skipping motion horizontal velocity with different structural quality
由图20 和图21 可知,当结构质量增大时,结构体每次触水滑跳入水深度增加,弹起速度和高度也会增大,导致每次滑跳落点之间的水平距离加大。 在相同的时间和距离内,随着结构质量的增加,触水滑跳的次数减少。 由图22 可知,质量为1.0 kg 时,第1 次触水滑跳后水平速度降为23.64 m/s,衰减率为5. 44%;质量为1. 554 kg时,第1 次触水滑跳后水平速度降为23. 5 m/s,衰减率为6%;质量为3.0 kg 时,第1 次触水滑跳后水平速度降为23. 22 m/s,衰减率为7. 12%。当结构质量增大时,每次触水弹跳水平速度的下降量增大。
3.4.2 初始高度对滑跳运动的影响
为了得到初始高度对球冠体滑跳运动的影响规律,在不改变其他分析参数的情况下,改变初始高度H0分别为0. 5,1. 0,1. 5 m,仿真总时长为1.3 s。 不同初始高度的滑跳轨迹对比如图23 所示,不同初始高度的滑跳垂向速度时历对比如图24所示,不同初始高度的滑跳水平速度时历对比如图25 所示。

图23 不同初始高度的滑跳轨迹对比Fig.23 Comparison of skipping motion trajectories with different initial heights
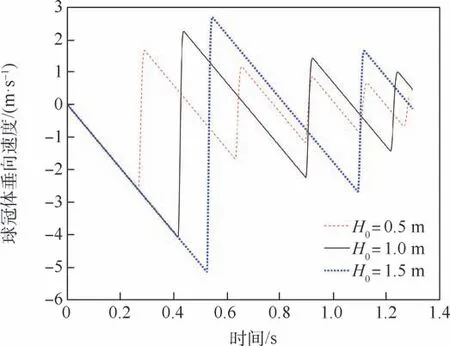
图24 不同初始高度的滑跳垂向速度时历对比Fig.24 Time history comparison of skipping motion vertical velocity with different initial heights
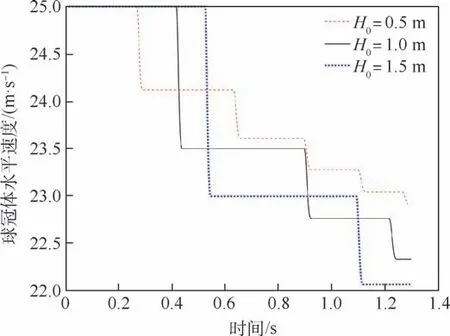
图25 不同初始高度的滑跳水平速度时历对比Fig.25 Time history comparison of skipping motion horizontal velocity with different initial heights
通过图23 和图24 可知,初始抛出高度增加,结构体每次触水滑跳入水深度增加,触水弹起的高度和弹起速度也随之增大,导致每次滑跳落点之间的水平距离加大,在同样的时间和距离内触水滑跳的次数变少。 通过图25 可知,初始高度为0. 5 m 时,第1 次触水滑跳后水平速度降为24.12 m/s,衰减率为3.52%;初始高度为1.0 m时,第1 次触水滑跳后水平速度降为23. 5 m/s,衰减率为6%;初始高度为1.5 m 时,第1 次触水滑跳后水平速度降为23. 0 m/s,衰减率为8%。初始抛出高度的增大,会导致每次触水弹跳水平速度的下降量增加,动能损耗增多。
3.4.3 水平抛出速度对滑跳运动的影响
为了得到水平抛出速度对球冠体滑跳运动的影响规律,在不改变其他分析参数的情况下,改变球冠体的水平抛出速度V0分别为20,25,30 m/s,仿真总时长为1.3 s。 不同水平抛出速度的滑跳轨迹对比如图26 所示,不同水平抛出速度的滑跳运动垂向速度时历对比如图27 所示。
通过图26 和图27 可以看出,随着水平抛出速度的增大,相同时间内球冠体的水平位移增加,每次触水滑跳的弹起高度和弹起速度也会增加,相同时间和距离内触水滑跳的次数减少。

图26 不同水平抛出速度的滑跳轨迹对比Fig.26 Comparison of skipping motion trajectories with different horizontal throw speeds
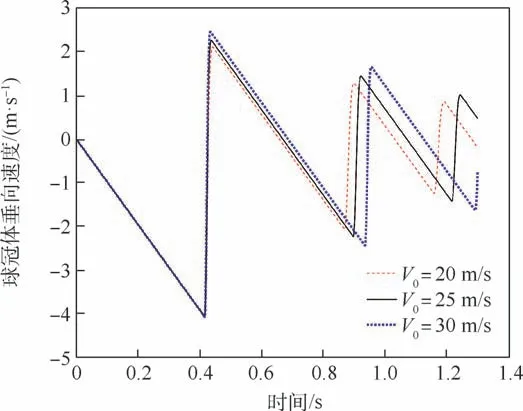
图27 不同水平抛出速度的滑跳垂向速度时历对比Fig.27 Time history comparison of skipping motion vertical velocity with different horizontal throw speeds
3.4.4 半径大小对滑跳运动的影响
为了得到半径大小对球冠体滑跳运动的影响规律,在不改变其他分析参数的情况下,改变球冠体的半径大小r0分别为0.1,0.152 4,0.2 m,仿真总时长为1.3 s。 不同半径大小的滑跳轨迹对比如图28 所示,不同半径大小的滑跳运动垂向速度时历对比如图29 所示,不同半径大小的滑跳运动水平速度时历对比如图30 所示。
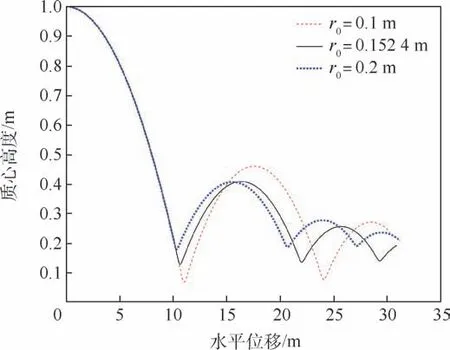
图28 不同半径大小的滑跳轨迹对比Fig.28 Comparison of skipping motion trajectories with different radius sizes
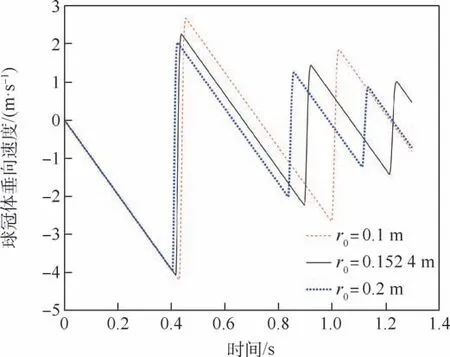
图29 不同半径大小的滑跳垂向速度时历对比Fig.29 Time history comparison of skipping motion vertical velocity with different radius sizes
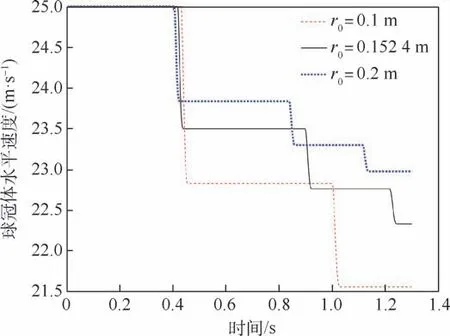
图30 不同半径大小的滑跳水平速度时历对比Fig.30 Time history comparison of skipping motion horizontal velocity with different radius sizes
通过图28 和图29 所示,随着球冠体的半径减小,结构每次触水弹跳的入水深度增加,每次触水滑跳的高度和弹起速度也随之增加,导致每次触水滑跳运动之间飞行的距离增大,在同样的时间或者距离内触水弹起的次数减少。 此外,通过图30 可知,球冠体半径为0.1 m 时,第1 次触水滑跳后水平速度降为22. 83 m/s,衰减率为8.68%;球冠体半径为0.152 4 m 时,第1 次触水滑跳后水平速度降为23.5 m/s,衰减率为6%;球冠体半径为0.2 m 时,第1 次触水滑跳后水平速度降为23.84 m/s,衰减率为4.64%,随着球冠体半径的减小,结构每次触水弹跳水平速度的下降量增大,动能损耗增多。
3.5 弹性效应的影响
为了得到结构体弹性效应对球冠体滑跳运动的影响规律,在不改变其他分析参数的情况下,考虑结构体的弹性效应并进行时域仿真分析。 在考虑结构弹性效应的影响时,发现实心高刚度材料的球冠体几乎没有弹性效应。 为了放大结构的弹性效应,将实心球冠体改为空心,壳体的厚度为1.0 mm,材料刚度同时降低,弹性模量改为0.7 MPa,泊松比为0.33。 进行模态分析后得到,空心球冠体的一阶弹性模态频率为12.32 Hz,二阶弹性模态频率为14.91 Hz,仿真总时长为1.1 s。 有无弹性效应时结构体第1 次触水所受垂向流场载荷时历对比如图31 所示,有无弹性效应时结构体第1 次触水所受水平方向流场载荷时历对比如图32所示,有无弹性效应的滑跳轨迹对比如图33 所示,有无弹性效应的滑跳运动垂向速度时历对比如图34所示,有无弹性效应的滑跳运动水平速度时历对比如图35 所示。 考虑弹性效应时,球冠体最低点的弹性变形时历图如图36 所示。
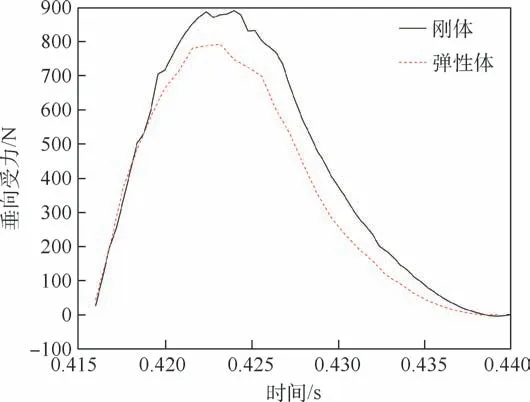
图31 有无弹性效应的第1 次触水垂向受力时历对比Fig.31 Time history comparison of vertical stress in the first contact with water with or without elastic effect
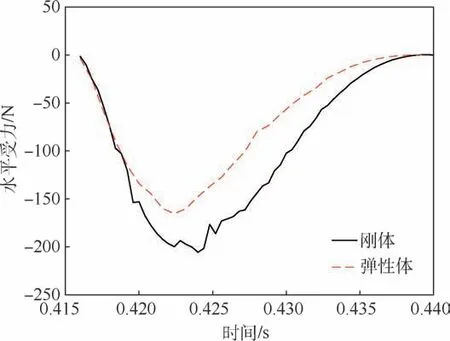
图32 有无弹性效应的第1 次触水水平受力时历对比Fig.32 Time history comparison of horizontal stress in the first contact with water with or without elastic effect
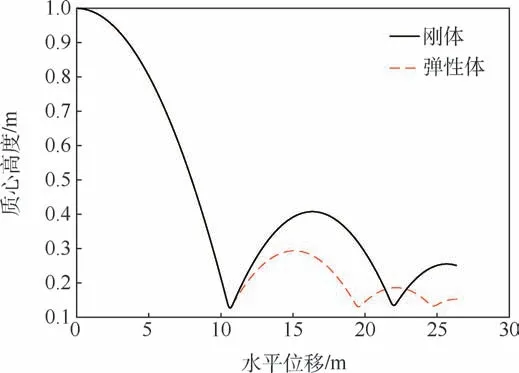
图33 有无弹性效应的滑跳轨迹对比Fig.33 Comparison of skipping motion trajectories with or without elastic effect

图34 有无弹性效应的滑跳垂向速度时历对比Fig.34 Time history comparison of skipping motion vertical velocity with or without elastic effect
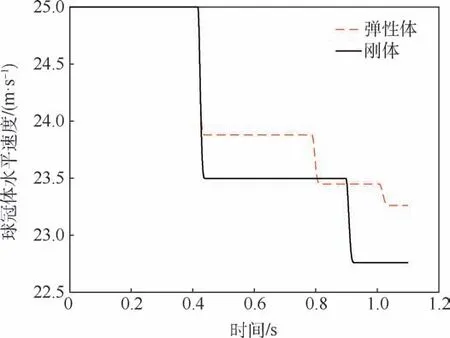
图35 有无弹性效应的滑跳水平速度时历对比Fig.35 Time history comparison of skipping motion horizontal velocity with or without elastic effect
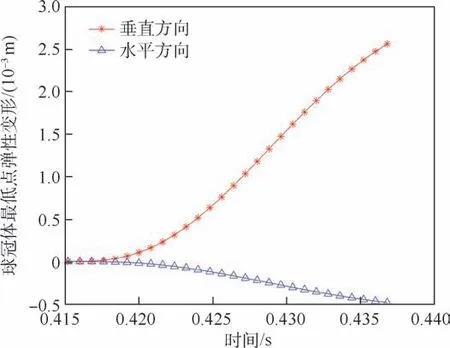
图36 球冠体最低点的弹性变形时历曲线Fig.36 Time history curves of elastic deformation at the lowest point of spherical crown
通过图31 和图32 可知,考虑结构体的弹性效应之后,触水滑跳过程中流体作用在结构上的垂向载荷和水平方向载荷都有所减小,这也影响了结构体的滑跳运动。 垂向受力峰值由887.2 N降为792.7 N;水平方向受力峰值由-205.5 N 变为-165.3 N。 通过图33 和图34 可知,考虑弹性效应之后,球冠体每次触水滑跳的弹起高度降低,弹起速度也降低。 同时,每次触水弹起飞行的距离也会降低,在同样的时间或者距离内触水弹起的次数会增多。 通过图35 可以知道,考虑弹性效应之后, 第1 次触水滑跳后水平速度降为23.88 m/s,衰减率为4. 48%。 这说明考虑弹性效应后,球冠体每次触水滑跳水平速度衰减率降低。
通过图36 可知,球冠体最低点的垂向弹性形变为一直向上压缩,水平方向弹性形变为向后变形。 这与高速斜入水冲击载荷的作用方向一致。此外,垂直方向的弹性形变大于水平方向的弹性形变。
4 结 论
1) 本文基于边界元法,建立了一种三维结构体近水面滑跳运动的时域数值仿真方法。 该方法既可以应用于任意外形的三维结构体,也拥有较高的计算效率。 针对三维刚性球冠体的近水面滑跳运动进行了时域数值仿真,得到了对应的运动特性,验证了该方法的可行性和准确性。 在此基础上,可以进一步应用于击水式飞行器的滑跳弹道仿真分析。
2) 在球冠体的每次触水过程中,高速斜入水冲击载荷提供的阻力和升力,均快速达到峰值并逐渐减小,且垂向受力相较于水平方向受力会先一步达到峰值。 垂向受力的数值相对较大,水平方向的受力数值相对较小。
3) 初始参数对球冠体滑跳运动有较大的影响。 随着结构质量的增加,每次触水滑跳的弹起速度和高度增大,每次滑跳落点之间的水平距离加大,在相同的时间和距离内触水滑跳的次数减少,每次触水弹跳水平速度的衰减量增大。 初始高度的增加,会导致每次触水滑跳的弹起高度和弹起速度增大,每次滑跳落点之间的水平飞行距离加大,在同样的时间和距离内触水滑跳的次数变少,每次触水弹跳水平速度的衰减量增大。 随着水平抛出速度的增大,每次触水滑跳的弹起速度和高度增大,每次滑跳落点之间的水平距离加大,在相同的时间和距离内触水滑跳的次数减少。球冠体半径的减小,会导致每次触水滑跳的弹起高度和弹起速度增加,每次触水弹跳运动之间飞行的距离增大,在同样的时间或者距离内触水弹起的次数减少,每次触水弹跳水平速度的衰减量增大。
4) 弹性效应对球冠体滑跳运动有一定的影响,考虑弹性效应后,会减小高速斜入水冲击载荷,导致球冠体弹起速度和高度降低,且滑跳过程中水平速度衰减率减小。 因此,对弹性效应较明显的结构体进行滑跳运动数值仿真时,应当考虑弹性效应的影响。

