《线性代数》学习中三次方程求根方法探讨

万前红

(湖南工商大学理学院，湖南 长沙 410205)

《线性代数》是高等学校理科、工科及经济类等非数学专业本科生必须学习的一门公共基础课程，该课程具有概念多、抽象、逻辑严密等特点线性代数知识体系中，包含两个重要内容，一个是线性方程组解的判别，另一个是方阵特征值的计算众所周知，《线性代数》是以线性方程组为主线发展起来的，从而线性方程组解的判别与求解对于学习线性代数十分重要方阵特征值与特征向量是计算方阵高次幂、二次型化标准型的重要方法的基础

若一个实际问题转化成系数矩阵为方阵且含有参数的线性方程组，我们需要对其解进行判别，如例1

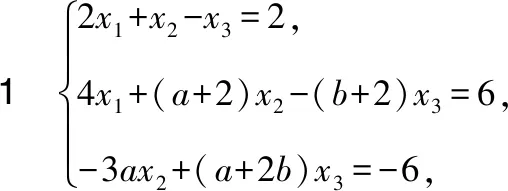
针对例1，我们可以使用初等变换法将系数矩阵化为行阶梯形或行最简形，然后利用系数矩阵的秩与增广矩阵的秩以及它们与未知数之间的关系来判别方程组的解但系数矩阵含有参数，不仅在化行阶梯形或行最简形的过程中容易出错，而且讨论含参数的系数矩阵与增广矩阵的秩以及它们与未知数之间的关系来判别方程组解的难度也不小又因为系数矩阵是方阵，所以我们可以考虑使用克莱姆法则来进行判定

对含有个未知量、个方程的线性方程组

(1)

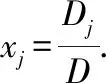
注：在克莱姆法则中，系数行列式=||不等于零，是方程组(1)有唯一解的充分必要条件

根据克莱姆法则，我们来解例1：

利用集合补集的计算，我们有：方程组无解或有无穷多解当且仅当=≠0或者=0

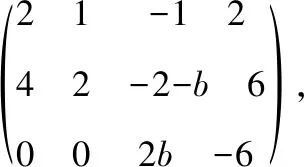
在解答例1的过程中，我们发现最关键的一步是计算系数矩阵的行列式不等于零，而此过程相当于计算一个三次方程根的补集

若要计算一个方阵的特征值，如例2

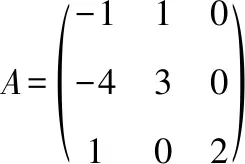
由线性代数知识可知，方阵的特征值是其特征多项式的根针对例2，即是求

的根

由此我们发现解决例1、例2均以求方程的根为基础很多学生对解决例1和例2的方法步骤是比较清晰的，但是却没有得到最后结果经过调查分析我们发现，主要问题在于学生不会计算高次方程的根下文就方程求根问题，结合线性代数知识列举几种方程求根方法

1 整系数多项式的有理根

该引理提供了一个求整系数多项式全部有理根的方法见下例3

为了更好地利用引理1求方程的有理根，我们需要下面引理：

设是次多项式方程()=0的重根的充分必要条件是()的阶导函数()()=0(=0,…,-1)，且()的阶导函数()()≠0

3求例2中方程-4+5-2=0的所有根

令()=-4+5-2,次数最高项的系数为1，因而因子为±1；常数项为-2，因而因子为±1,±2由引理1，方程的所有有理根可能为±1,±2经验证，2和1为方程的根

()的导函数′()=3-8+5经验证，1为′()的根,2不是″()的根,由引理2可知，1为()的二重根因此我们找到了()的三个根：2，1，1由代数学基本定理可知(参见[1])，三次方程共有3个根，因此我们找到了()的所有根

需要说明的是，该引理中虽然要求多项式的系数为整数，但是对一般的方程，我们可以通过系数处理，使其变为整系数

2 利用行列式的性质寻找根

如果行列式中两行(列)元素对应成比例，那么行列式值为零

我们用一个例子来说明如何利用该性质求方程的根

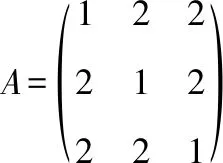
矩阵的特征方程为

若

则行列式的第1行和第2行元素对应成比例，由性质1可知，此时-1=-2满足方程，即=-1是方程的根所以

|-|=-3-9-5=(+1)(),

其中()可按多项式的除法得到具体计算如下：

即()=-4-5所以|-|=(+1)(-4-5)=(+1)(-5)从而，方阵的特征值为=5，==-1

若行列式中有一行(列)元素全为0，则行列式的值为0

我们以例2为例说明该性质的应用

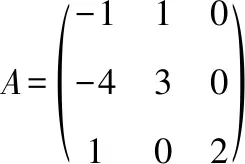
此题还可以按下面性质来考虑：

行列式的值等于其某一行(列)的元素与其对应的代数余子式乘积的和

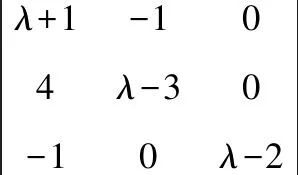
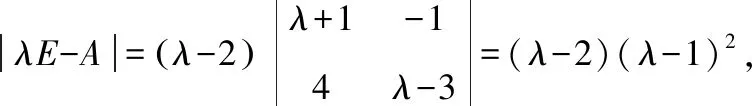
从而矩阵的特征值为2，1(二重)

性质3提示我们，在处理高阶行列式时，我们可利用行列式的初等变换，将行列式的某行(列)化成只有一个元素不为零然后利用性质3，即可分离出特征多项式的一个因式，从而找到特征多项式的一个根且可以一直重复此步骤，直到将行列式的阶数降为2阶为止

3 直接利用三次方程的通用求根公式

3.1 将一般三次方程转化为不完全三次方程

3.2 不完全三次方程求根

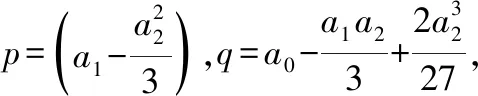
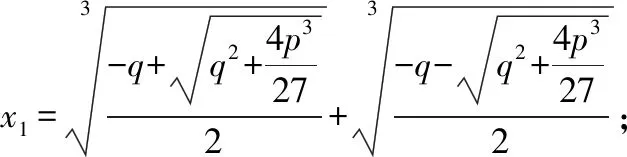
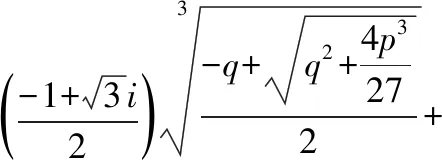
其中是虚数单位该方法的最大优势是可以找出三次方程无理根和复数根三次方程的根还有其余表示形式，参见[4]

5求+1=0的全部根

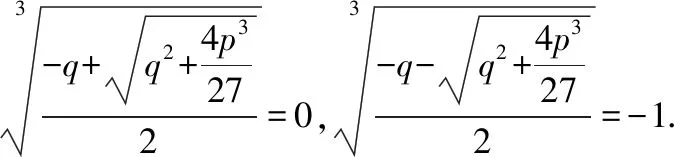
利用因式分解+1=(+1)(-+1)及二次方程的求根公式，很容易验证上面用不完全三次方程求根公式法计算出来的根是正确的

4 结 语

线性方程组在现实生活中的应用是非常广泛的,不仅可以广泛地应用于数学自身，还可以应用于经济学、统计学、工程学、计算机科学、物理学、力学、通信、航空等学科和领域，相关问题均可将问题转化为线性方程组求解特征值与特征多项式也广泛地应用于数学自身，如，Fibonacci数列通项公式计算、矩阵高次幂的运算、二次型的标准化等，同时也应用于其他领域，如统计学中的主成分分析法本文所介绍的三次方程求根方法为线性方程组解的判别、特征值的计算提供了更多途径，几种方法之间可以融合起来使用，且均可以应用到高次方程的求解，为我们奠定学习线性代数的基础