非球形颗粒两相流的数值模拟研究进展

崔智文 王 泽 蒋新宇 赵立豪

清华大学航天航空学院工程力学系, 北京 100084

1 引 言

颗粒两相流常见于工业生产、自然环境和生物医学等领域. 20 世纪以来, 颗粒两相流相关的研究主要集中在球形颗粒问题, 且现在依然是两相流领域中最活跃的方向之一. 在这些研究中颗粒的形状因素通常被忽略, 而简化成球形, 并且研究关注的重点主要是颗粒在流动中的聚集和输运现象. 然而, 在实际流动问题中颗粒形状往往不规则, 颗粒的非球形特性对颗粒取向与转动行为的影响不可忽略, 比如在纸张制造过程中纸纤维的取向(Lundell et al. 2011a, Håkansson et al. 2014)以及纤维增强材料制备过程中纤维的排列(Cheung et al. 2009, Soutis 2005)均会对最终成品的力学性能产生重要的影响; 大量的实验与数值模拟结果表明, 纤维以及聚合物对壁湍流的减阻和调制作用与其取向行为密切相关(Paschkewitz et al. 2004, 2005a, 2005b); 不同环境温度和湿度下, 形成的冰晶具有不同的形状, 会影响冰晶的碰撞融合以及雨雪的形成(Heymsfield 1977, Jucha et al. 2018); 海洋和湖泊中浮游生物往往具有形状多样性等(Pedley & Kessler 1992,Saintillan 2018, Qiu et al. 2019, Ardekani et al. 2017a).

近代有关非球形颗粒两相流的理论研究最早可以追溯到Jeffery(1922)在Stokes 流中推导的椭球颗粒受剪切作用的力矩方程, 随后在Batchelor(1970)和 Brenner(1961, 1963b)的努力下, 逐渐完成了Stokes 流动中椭球颗粒的阻力及颗粒对流体产生的额外应力(Batchelor 1970, Brenner 1974)的理论表达式. 由于当时计算机计算能力的限制, 这些研究主要集中在椭球形颗粒在极低雷诺数流动中运动的理论或实验研究. 随着计算机硬件水平的飞速提升以及高精度数值模拟方法的快速发展, 复杂流场中大规模非球形颗粒运动的高精度数值模拟得以实现. 研究的颗粒形状、尺寸以及流场类型日益多样化. 然而, 相较于球形颗粒两相流的研究, 非球形颗粒两相流的数值模拟研究依然处于起步阶段, 而非球形颗粒的各向异性的形状特性也引入了更多的运动行为 (比如转动、取向等)以及颗粒参数范围(比如颗粒形状等). 这使得非球形颗粒两相流问题变得更加复杂且难以分析, 进而给非球形颗粒两相流的研究带来了较大的挑战. 目前, 有关非球形颗粒两相流的数值模拟研究主要集中以下三个方面: (1) 单个颗粒行为的研究, 建立对非球形颗粒在不同流场中的运动学和动力学特征以及颗粒与流场之间的相互作用的基本认识, 辅助点颗粒模型的建立; (2) 多颗粒行为研究, 以了解颗粒与颗粒、颗粒与流场间的相互作用, 以及建立相关模型; (3) 研究大规模颗粒群在复杂流场 (如湍流) 中的运动行为, 通过统计学方法描述颗粒在流场中的行为特征, 以建立与完善非球形颗粒的欧拉模型.

目前, 非球形颗粒两相流的数值模拟主要基于欧拉-拉格朗日的求解框架. 在该框架下, 流体相的Navier-Stokes 方程在欧拉网格上进行求解, 而颗粒相则通过拉格朗日追踪方法去描述每一个颗粒的行为. 颗粒在拉格朗日观点下的求解能准确地描述颗粒的平动、取向与转动行为, 进而可以帮助研究者更加直观地认识非球形颗粒复杂的运动行为与流场的关系. 基于该框架, 根据不同的颗粒计算方法, 颗粒相的模拟可划分为点颗粒方法与全分辨颗粒方法. 前者用质点替代具体形状的颗粒, 流体与颗粒之间的相互作用均通过相应的理论模型实现. 而后者需要完全分辨颗粒与流体的界面, 流体与颗粒之间的相互作用通过全分辨数值模拟直接实现. 近些年来, 国内外学者使用这两类方法进行了大量直接数值模拟的研究, 使得人们对非球形颗粒在复杂流动中的行为规律有了初步认识.

本文针对非球形颗粒两相流数值模拟的研究进展进行综述. 文章的主体分为三个部分: 第一部分介绍非球形颗粒两相流研究的基本概念、数值方法和理论模型; 第二部分介绍非球形颗粒在简单基本流场(均匀来流、静止流场和剪切流)和复杂湍流场(均匀各向同性湍流和壁湍流)中的运动学行为; 第三部分针对湍流中非球形颗粒取向与转动行为、非球形颗粒对湍流的减阻调制作用的机理展开讨论. 最后, 对未来值得研究的工作提出一些建议.

2 数值模拟方法

在本综述讨论的颗粒两相流中, 颗粒均为离散相. 本节将主要介绍欧拉-拉格朗日方法中非球形颗粒的描述方法、理论模型以及相关的数值模拟手段. 通常, 流体的求解可以采用有限差分方法、有限体积方法、谱方法等常见的数值方法. 而颗粒的求解根据建模的方法可以大致分为点颗粒方法与全分辨颗粒方法. 点颗粒方法用质点替代具体的颗粒, 流体与颗粒之间的相互作用均通过相应的力学模型实现. 而全分辨颗粒方法则完全分辨颗粒的形状, 流体与颗粒之间的相互作用也通过数值模拟直接实现. 两种方法的使用条件主要由研究的主要问题确定. 通常点颗粒方法适合颗粒尺寸小于流体的最小特征尺度, 比如湍流中的Kolmogorov 长度尺度, 此时颗粒雷诺数较小, 颗粒尾部不出现明显的涡脱落, 颗粒的受力以及颗粒对流场的影响可以通过点颗粒模型比较准确地给出. 而全分辨颗粒方法适合颗粒尺寸大于流体最小特征尺寸, 以捕捉点颗粒模型无法表征的流体惯性特征和对流场的反馈影响. 点颗粒方法通常使得单颗粒的计算量较低, 因此,非常适合大量颗粒 (百万量级) 的计算, 但点颗粒的模型适用范围有限, 例如颗粒尺寸足够小、颗粒雷诺数须满足模型要求等. 而全分辨方法通常可以较为精确地模拟单个颗粒的行为, 但每个颗粒的计算成本高, 尤其是对于尺寸远小于流场尺度的颗粒, 难以实现大规模颗粒的计算. 目前这两种方法在研究中是相辅相成的关系, 一方面可以通过全分辨方法提炼点颗粒的模型, 另一方面可利用完善后的点颗粒模型进行大规模颗粒两相流的模拟.

2.1 非球形颗粒的基本方程

2.1.1 坐标系的定义

为了准确描述非球形颗粒的行为, 一般需要描述颗粒空间位置以及空间的取向(或姿态).在本文使用三种参考系来描述单个颗粒的运动 (如图1 所示) , 它们分别是:

(1) 惯性参考系 : 用来描述连续流场以及颗粒的平动行为.

(2) 颗粒参考系 : 以颗粒质心位置为原点, 轴分别对齐颗粒的主轴. 颗粒的转动行为通常在该参考系下求解.

(3) 随动参考系 : 以颗粒质心位置为原点,x′′,y′′,z′′轴分别与惯性参考系中的x,y,z轴平行. 与惯性参考系之间相差一个平动位移.

其中, 颗粒参考系与随动参考系之间通过一个旋转张量R进行转换, 即

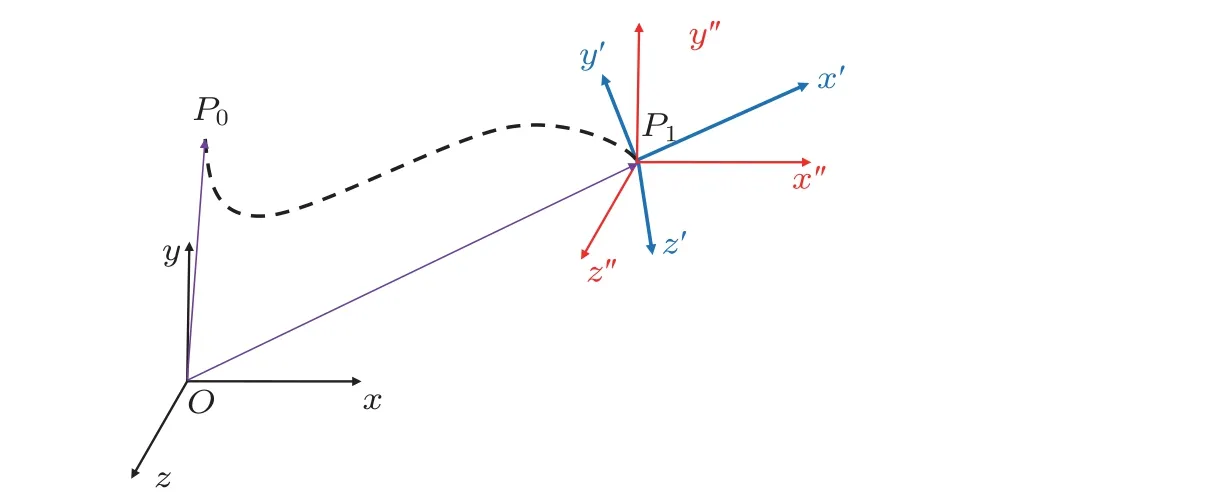
图1描述颗粒运动的参考系: 惯性参考系 〈 x,y,z〉 , 颗粒参考系 〈 x′,y′,z′〉 以 及随动参考系〈x′′,y′′,z′′〉

同时, 颗粒的取向、转动与速度均由矢量进行描述. 对于矢量而言, 其在惯性参考系与随动参考系下的表达相同. 为了简化标记, 在不引入歧义的情况下, 通常用惯性参考系的描述方法来取代随动参考系, 进而对颗粒的运动行为以及相关变量进行描述. 因此, 对于惯性参考系描述的矢量p满足

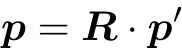
其中‘(·)′’代表颗粒参考系下的变量, 下同. 对于惯性参考系中的二阶张量H满足

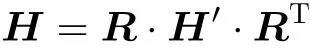
2.1.2 平动与转动方程

根据牛顿第二定律, 颗粒的平动与转动方程分别表示为

式中,mp为颗粒质量,I为颗粒的转动惯量,v为颗粒的平动速度,为颗粒的转动角速度,F与T分别为作用在颗粒上的合外力与合外力矩. 颗粒的转动行为一般在颗粒坐标系中进行求解, 即

如果颗粒的合外力与合外力矩可以准确得到, 颗粒的运动行为可以通过式(1)与式(2)进行求解得到.

2.1.3 颗粒取向求解

从颗粒参考系到惯性参考系的旋转矩阵可由欧拉四元数E=[e0,e1,e2,e3] 来表示, 即

欧拉四元数随时间推进的方程为

式中

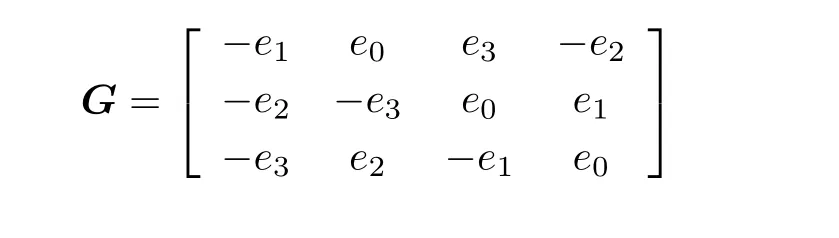
2.1.4 颗粒形状

非球形颗粒通常具有复杂的外形. 在非球形颗粒的研究中, 主要使用椭球颗粒模型对非球形颗粒进行近似. 主要的原因包括:

(1) 椭球颗粒是最简单的非球形颗粒模型. 近一个世纪以来, 科学家们通过椭球坐标系变换以及相关椭球谐函数等数学方法得到一些椭球颗粒的作用力的解析表达式. 因此, 椭球颗粒作为非球形颗粒动力学的理论研究的基础模型, 拥有比较强大的数学工具. 尽管如此, 非球形颗粒两相流的研究道路依然非常困难, 目前得到的理论模型依然有限.

(2) 大量的直接数值模拟以及实验研究表明, 椭球颗粒模型能比较好地捕捉到部分非球形颗粒(非椭球形状)的运动特性, 比如圆盘、纤维、圆柱等. 研究椭球颗粒的运动行为能够帮助人们认识形状的各向异性所带来的复杂动力学行为.

在本文中, 椭球颗粒表示为

2.1.5 无量纲参数

在非球形颗粒两相流中常用的无量纲参数如下.

(1) 颗粒雷诺数Rep: 基于颗粒与流体之间相对滑移的速度与颗粒直径定义的无量纲数, 即Rep=2|uf-v|rp/ν. 其中rp为颗粒的参考半径(通常选取等效半径或者颗粒的最大半径).

(3) 平动Stokes 数St: 用来反映颗粒的平动惯性,St=τp/τf.τp与τf分别表示颗粒的平动弛豫时间与流体特征时间尺度.

(4) 转动Stokes 数Str: 主要在剪切流中使用, 用来反映颗粒的转动惯性,即Str=ρpsrp2/μ.

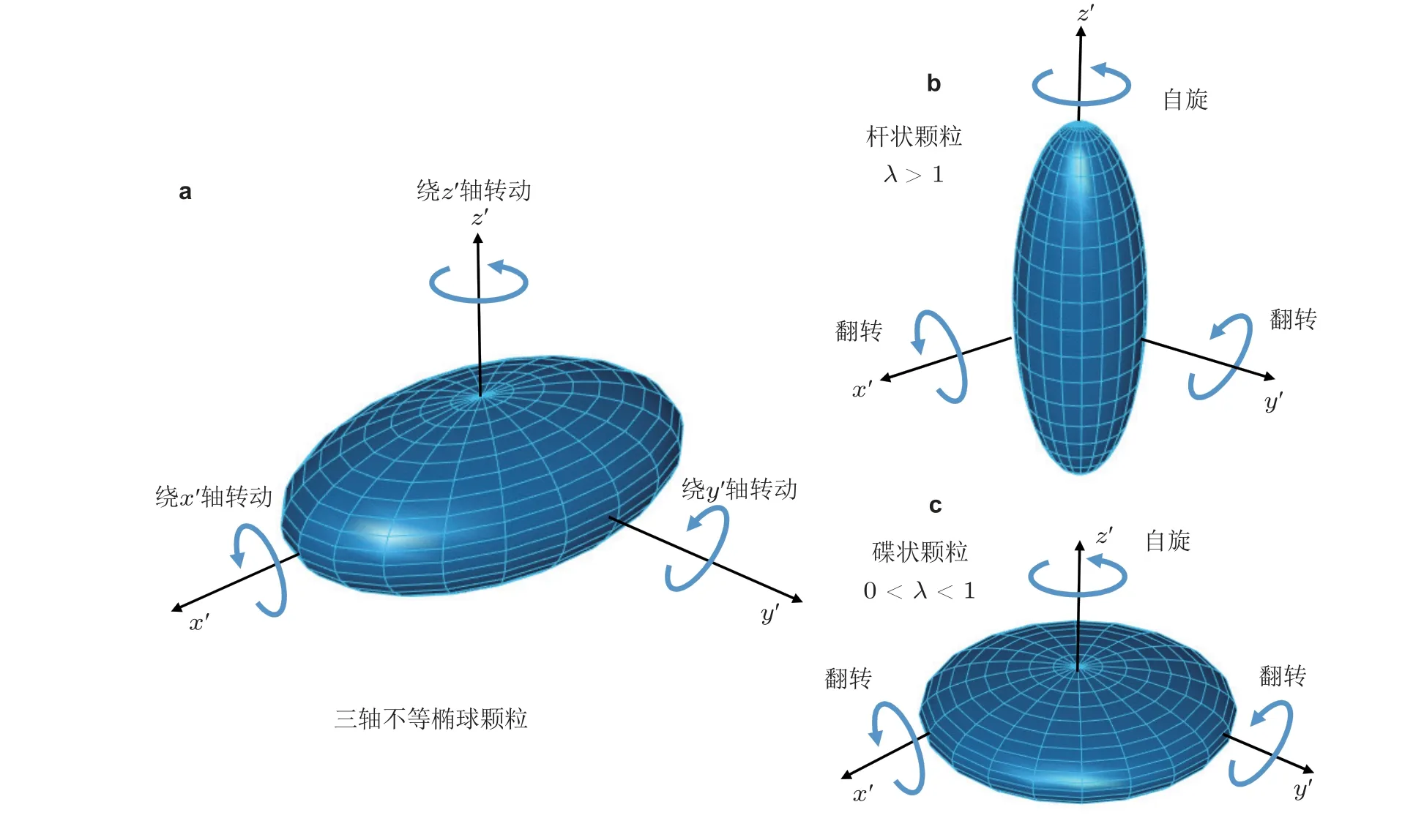
图2椭球颗粒模型示意图.(a)三轴不等颗粒, (b)杆状颗粒, (c)碟状颗粒

(5) 密度比D: 表示颗粒与流体密度之比, 即D=ρp/ρf.

需要注意的是在不同的文献中雷诺数的定义稍有差别. 在绝大部分问题中特征长度选为颗粒的直径, 但在有些理论推导的模型中往往选取颗粒的半径作为特征长度. 本文已经将该差别进行了统一, 但为了使形式与原文献保持一致以方便读者查阅, 一些地方保留了原文献中的定义,相关的差别将会在需要的时候提及.

2.2 点颗粒方法

2.2.1 基本思路

点颗粒, 顾名思义, 就是用质点替代复杂形状颗粒且同时考虑颗粒取向与转动行为. 如果研究的颗粒的尺寸远小于流动的特征尺度, 点颗粒是一种非常有效的方法(Maxey 2017). 该方法通常需要适当的理论或经验模型来描述流体与颗粒之间的相互作用, 颗粒与流体的相互作用主要受到颗粒相的体积分数和质量分数的影响(Balachandar & Eaton 2010). 常见的耦合方式如下.

(1) 单向耦合: 当体积分数和质量分数很小时, 即颗粒稀疏悬浮, 颗粒相对流体的反馈作用可以忽略, 只需考虑流体对颗粒的作用, 即流体作用在颗粒上的力与力矩;

(2) 双向耦合: 当体积分数或质量分数较大时, 颗粒相对流场的反馈作用不能忽略, 此时需要考虑颗粒对流体的作用并进行耦合, 比如力耦合(Crowe et al. 1977)、力矩耦合(Andersson et al.2012)以及应力耦合(Batchelor 1970, Brenner 1974);

(3) 四向耦合: 当颗粒相的体积分数进一步增大, 颗粒间的相互作用 (如碰撞, 团聚和破碎等) 也需要考虑. 此外, 还需要考虑颗粒与颗粒之间的相互作用力(比如静电力等).

点颗粒求解的基本流程与思路如下.

(1) 获取颗粒处未扰动流场. 当一步流场更新后, 需要通过适当的插值方法(比如线性插值、二阶拉格朗日插值等)从流场中获取颗粒位置处的未扰动流场的速度与速度梯度. 对于非球形颗粒而言, 颗粒位置处的速度梯度信息是非常必要的.

(2) 代入合适的颗粒受力模型, 计算颗粒的动力学方程.

(3) 如果进行双向耦合, 则需要计算颗粒对流场的反馈, 并将反馈力、力矩与应力耦合到流场中.

(4) 如果进行四向耦合, 则需要进行颗粒与颗粒的接触检测, 并施加相应的碰撞模型或者相互作用模型.

非球形颗粒两相流中常见的流体对颗粒的作用力以及颗粒对流体的反馈力模型将在第2.2.2 和2.2.3 小节进行介绍. 因为非球形颗粒之间的相互作用模型及机制相对复杂, 目前相关研究工作较少, 本文暂不讨论颗粒与颗粒之间的相互作用, 而有关颗粒与颗粒碰撞的模型可以参见第2.3.4 小节.

2.2.2 流体对颗粒的作用

流体对颗粒的作用通常体现为力与力矩的作用.

(1)力的作用

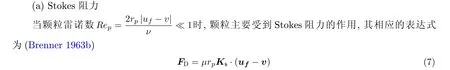
式中,Ks为无量纲Stokes 阻力系数矩阵,μ为流体的动力黏性系数,uf为颗粒处流体速度,为颗粒速度,rp为颗粒的参考半径(通常采用最大半径或者等效半径). 对于任意形状的微小椭球颗粒, 其Stokes 阻力系数矩阵是对称正定的(Brenner 1963b). 对于椭球颗粒模型, 在颗粒坐标系下, Stokes 阻力系数矩阵对角线上的元素非零, 且表示为

对于具有回转轴的椭球颗粒而言, 令形状参数ka=kb=1 ,kc=λ, 其中λ定义为颗粒回转轴长度与赤道轴长度之比. 那么与形状相关的参数α,β,γ和χ可以解析地用λ表达.

由于非球形颗粒的阻力系数矩阵的各向异性, Stokes 的阻力方向通常不与滑移速度共线. 与球形颗粒相比, 非球形颗粒受到的阻力不仅依赖颗粒与流体之间的速度滑移, 而且还取决于颗粒的取向.

同时, 为了反映颗粒趋近流体速度所需要的特征时间, 通常使用颗粒的弛豫时间进行描述,记为τp. 一般定义τp/τf为颗粒的Stokes 数, 记为St.当St趋近于零时, 意味着颗粒几乎完全跟随流体运动. 为了评估非球形颗粒的弛豫时间, 在湍流问题中, 假设颗粒在取向随机时(Brenner 1963b,Shapiro & Goldenberg 1993), 评估颗粒运动对流场变化的响应. 此时, 颗粒的弛豫时间τp可以定义为

(c) Saffman 升力

在颗粒雷诺数有限小的情况下, 强剪切会对运动的颗粒产生一个侧向的升力, Saffman(1965, 1968)最早通过奇异摄动理论得到了球形颗粒在简单剪切流中的升力模型, 由此称为Saffman 升力. 该模型预测的运动与实验中观察到的结果符合较好(Taylor 1923), 因此该模型逐渐得到了推广与应用. McLaughlin (1991), Bagchi 和Balachandar (2002), Magnaudet 与他的合作者们(Legendre & Magnaudet 1998, Magnaudet 2003, Magnaudet et al. 2003)对球形颗粒的Saffman 升力进行了改进以适应更加广泛的剪切流场. 而Harper 和Chang (1968)最早将Saffman 升力拓展到非球形颗粒, 并发现相关的升力系数矩阵与颗粒形状无关. 随后Fan 和Ahmadi (1995),Feng 和Kleinstreuer (2003), Cui Y 等 (2018, 2019, 2020) 在Harper 和Chang (1968)的基础上继续发展非球形颗粒的剪切诱导升力模型. 其中Cui Y 等(2020) 最近提出了一个比较高效求解杆状颗粒剪切升力的近似模型

然而, 目前的剪切诱导的升力模型与全分辨模拟的结果依然存在比较明显的差距(Cui Y et al. 2019). 至于该模型式(14)是否适合碟状颗粒依然有待研究. 目前在绝大部分点颗粒非球形颗粒两相流的理论研究问题中均未考虑剪切升力模型. 升力对非球形颗粒的动力学行为的影响依然有待进一步讨论.

(d) 重力与浮力

当考虑颗粒沉降等问题, 或颗粒Froude 数小于1, 即Frp=U/gτp ＜1 , 其中U为流体的特征速度,而g为重力加速度, 此时需要进一步考虑重力和浮力的影响(Sardina et al. 2012, Milici et al. 2014)

式中Fg为颗粒受到的重力与浮力的合力, 与mf分别为颗粒质量和颗粒排开流体的质量,g为重力加速度矢量.

(e) 经验公式

然而, 在一些实际工程问题中, 颗粒的雷诺数通常远大于1, 此时颗粒的受到的流体作用力无法通过理论的办法获得. 为了能够继续采用点颗粒方法, 就需要通过实验或者直接数值模拟的数据分析建立相应的经验模型. 而关于非球形颗粒受流体力和力矩的经验模型非常多, 在本文中不进行详细展开,具体可见Ouchene et al. (2015, 2016). 本文主要介绍一种基于椭球颗粒的经验模型(Zastawny et al. 2012). 不同的经验模型在形式上都具有相似性, 不同点在于系数的组合形式. 关于力的模型, 主要被分为阻力FD与升力FL. 在经验模型中, 颗粒阻力与滑移速度共线, 而升力作用在与滑移速度垂直的方向. 其对应的阻力系数与升力系数定义为

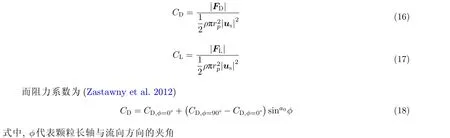
在式(19)与式(20)中的拟合系数ai与bi可参见(Zastawny et al. 2012). 其他相关的模型形式类似, 具体可参见(Mandø & Roséndahl 2010, Hölzer & Sommerfeld 2008).

(2) 力矩作用

(a) 黏性力矩

对于中心对称(即具有三个对称面)的非球形颗粒, 在Stokes 流的情况下, 其受到的黏性力矩为(Brenner 1974)

上式中,KR为旋转阻力系数张量,Θ为剪切阻力系数张量, 其中Θ为三阶张量,KR与Θ均与颗粒的形状有关. 对于任意三轴不等椭球颗粒而言, 在颗粒参考系中受到的黏性力矩为(Jeffery 1922)

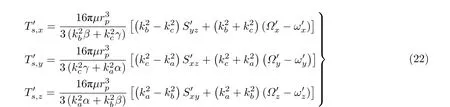
对于轴对称椭球颗粒, 形状有关的参数α,β与γ由表1 的表达式给出.

表1 轴对称椭球颗粒相关的形状参数

(b) 流体惯性力矩

(c) 经验公式

对于高雷诺数问题, 可将力矩分解成俯仰力矩Tp(pitch torque)与旋转力矩TR(rotation torque). 俯仰力矩主要是当颗粒回转轴的方向与流场速度方向不共线时产生, 而旋转力矩为颗粒相对于流体旋转时流场对颗粒产生的力矩(Zastawny et al. 2012). 在经验公式模型中, 通过定义俯仰力矩系数为

在Zastawny 等(2012)的工作中, 该系数与雷诺数以及攻角的关系为

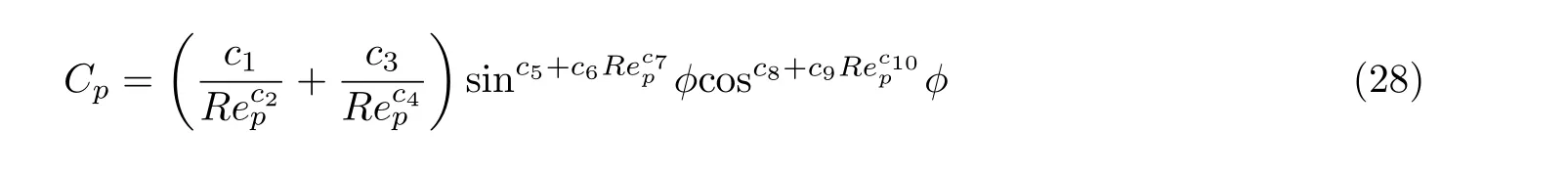
上式中拟合系数c1～c10可参见Zastawny 等(2012)的工作. 旋转力矩系数定义为

式中Ωs为流体与颗粒之间的相对滑移角速度, 即Ωs=Ω-ωp. 该系数与颗粒旋转雷诺数的关系为

式中颗粒旋转雷诺数为ReR=4rp2|Ωs|/ν, 系数r1～r4参见Zastawny 等(2012)的工作. 其它相关的拟合形式的力矩形式可参见文献(Ouchene et al. 2015, 2016; Yin et al. 2003).

(3) 其他受力模型

根据经典的Maxey-Riley 小球受力模型(Maxey & Riley 1983), 非定常流动中点颗粒模型还需要进一步考虑压力梯度力、附加质量力、Basset 历史力效应项等. 当颗粒密度远大于流体密度时, 压力梯度力与附加质量力的作用可以忽略不计. 对于颗粒密度接近流体密度或者小于流体密度时, 压力梯度力以及附加质量力的作用不可忽略. 在当前综述的工作中描述的点颗粒均是密度比远大于1 的情况, 暂不考虑压力梯度力与附加质量力的影响. Basset 力反映了颗粒在加速过程中边界层发展滞后所导致的“历史”效应的作用, 但往往因为其在计算中实现困难以及该项仅在具有较大滑移速度变化时比较重要, Basset 力通常在计算中被忽略. 近期的研究文章(Olivieri et al. 2014, Daitche 2015, Prasath et al. 2019)表明Basset 力在颗粒输运中的重要影响. 然而,Basset 历史力效应项是基于球形颗粒得到的, 对于非球形颗粒而言, 目前还没有针对一般椭球颗粒的模型. Lawrence 和Weinbaum (1986)通过摄动理论对近球形颗粒的小偏心率进行展开, 推导了近球形椭球颗粒的历史力模型, 并发现对于非球形颗粒而言, 除了Basset 历史效应力外还存在新的历史力项. 相关的推导与解释可参见论文Lawrence 和Weinbaum (1986, 1988). 目前,在大部分非球形点颗粒模拟中, 依然不考虑历史力效应, 而历史力对非球形颗粒的影响还有待进一步分析.

2.2.3 颗粒对流体的作用

颗粒对流体的反馈作用主要通过力耦合、力矩耦合和应力耦合等方法实现, 对应的实现方法如下.

(1) 力耦合

力耦合是基于牛顿第三定律的传统双向耦合方法, 广泛应用于惯性颗粒与流体相互作用的数值模拟中. 该方法的基本思想是将颗粒所受到的流体作用力作为颗粒对流体的反馈力. 反馈力的实现是将某个网格内所有颗粒的反作用力 -F进行体积平均 (或者加权平均) 以得到作用于流体相的欧拉网格点的体积力( Crowe et al. 1977, Maxey et al. 1997, Boivin et al. 1998, Vreman 2015 )

其中,Δ为网格体积,Fil为该网格体积内第l个颗粒所受流体作用力,np为该网格体积内的颗粒数. 将体积力fip添加到流体动量方程的右端项, 便实现了基于力耦合方法的双向耦合.

(2) 力矩耦合

Andersson 等 (2012)在力耦合的基础上提出了力矩耦合方法, 认为除了将颗粒的点力作为反馈力外, 还应该考虑颗粒所受力矩对流体的反作用. 和力耦合方法相似, 单个颗粒受到流体施加的力矩N, 则该颗粒对周围流体产生反馈力矩 -N, 其可表示为作用于流体微团的表面力. 体积为Δ的网格内, 颗粒产生的反对称应力为

(3) 应力耦合

不同于大密度比的惯性颗粒, 小尺寸的近中性悬浮颗粒可视为无惯性颗粒, 因此颗粒对流体的反馈力和力矩可以忽略. 但刚性颗粒由于不可变形, 还会通过额外的颗粒应力影响附近流体.稀疏悬浮液中的这种应力可以通过对应力子(stresslet)进行局部体积平均得到(Batchelor 1970).尽管应力子不像力矩和点力那样与颗粒的动力学直接相关, 但应力子实质上代表刚性颗粒对流体应变运动的抵抗 (Guazzelli & Morris 2011). Brenner (1974)推导了一般轴对称颗粒的应力子形式, 这里只简单介绍轴对称椭球颗粒的对应表达式

2.2.4 无惯性椭球颗粒模型

式中,vs为颗粒的Stokes 沉降速度. 对于小惯性颗粒的沉降问题, 颗粒的速度可以通过颗粒当地的流场速度加上沉降速度获得(Qiu et al. 2019). 若不考虑重力作用, 颗粒近似跟随流体轨迹线.

此时颗粒的转动, 也直接由当地的速度梯度与颗粒取向决定

类似惯性颗粒的求解, 颗粒的取向相关的欧拉四元数由式(5)推进.

对于轴对称的椭球颗粒, 颗粒的取向行为也可以直接通过求解颗粒回转轴方向方程获得, 即

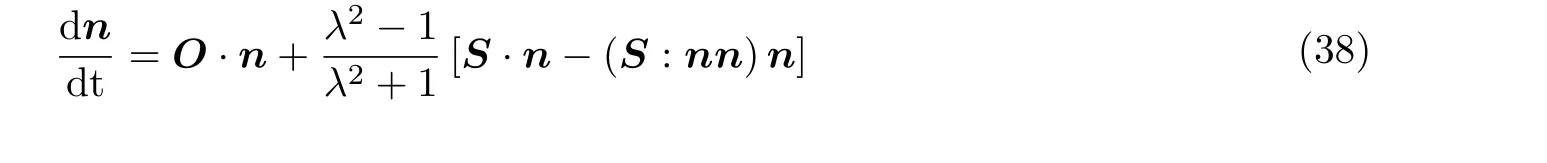
2.3 全分辨颗粒方法

对于尺寸大于流动最小尺度 (kolmogorov 尺度) 的颗粒, 以及一些形状不规则的颗粒, 它们与流体的相互作用就难以再用点颗粒的方法描述了, 这时就需要借助全分辨的方法来对颗粒两相流进行模拟. 这种模拟方法在颗粒表面施加无滑移边界条件, 完全分辨出颗粒的形状、尺寸,进而分辨出颗粒周围的流场以及颗粒-流体间的相互作用. 基于完全分辨的方法研究颗粒两相流能够最准确地捕捉颗粒-流体之间的相互作用(Tenneti & Subramaniam 2014), 同时也可以用于对基于点颗粒的方法进行建模、验证, 具有重要的学术价值和研究意义.

完全分辨的颗粒两相流问题中颗粒通常被视为刚体, 其与流体的相互作用就可以描述为流体中自由运动刚体的流固耦合问题, 如图3 所示, 其中Si代表颗粒表面, 小箭头代表颗粒运动方向. 对于该系统, 流体相用基于欧拉观点的不可压Naiver-Stokes(NS)方程描述, 颗粒相由基于拉格朗日观点的动力学方程(1)和(2)描述, 在不考虑其他外力 (如电磁力、电场力等) 的情况下,方程中的右端项合外力、合外力矩的形式为F=FH+Fint,T=TH+Tint, 其中FH,TH表示流体对颗粒的力和力矩,Fint,Tint表示颗粒之间相互碰撞的力和力矩. 而颗粒表面为流体提供了无滑移边界条件

式中uF代表颗粒表面的速度, 和ω分别为颗粒中心点平动速度和转动角速度,X为颗粒表面点的坐标, 而Xc为颗粒中心点坐标. 所以全分辨方式模拟颗粒两相流自然是双向 (不考虑颗粒碰撞) 或四向 (考虑颗粒碰撞) 耦合系统.

对于全分辨颗粒两相流问题的求解主要有两类方法, 即贴体网格类方法和非贴体网格类方法(Haeri & Shrimpton 2012, Kim & Choi 2019). 贴体类方法的思想很简单, 即在每一时刻都根据颗粒的位置划分流体网格, 并且根据颗粒的位置和当前运动设置流场的边界条件, 然后在流体区域内求解NS 方程. 到下一个时间步, 颗粒的位置发生变化, 则需要对空间网格进行重新划分以对流动进行求解, 如图4(a)所示. 这类方法的典型代表就是任意-拉格朗日-欧拉法 (ALE) .而后一类方法则通常需要两套网格, 即描述流场的背景笛卡尔网格和描述颗粒表面的拉格朗日网格, 如图4(b)所示的这类方法中, 背景的笛卡尔网格并不会因为颗粒的运动而发生改变, 因此不需要流体网格随颗粒运动的不断重新生成. 但是需要通过一些特殊的手段来处理流体-固体界面的边界条件. 这类方法的典型代表包括浸没边界方法 (immersed boundary method, IBM), 虚拟区域方法 (fictitious domain method, FDM) 和格子-玻尔兹曼方法 (lattice Boltzmann method,LBM). 贴体类方法在追踪运动的颗粒的过程中要不断更新求解流体方程的网格, 这个过程需要很大的计算量, 所以这类方法对颗粒两相流的数值模拟应用目前还仅限于二维(Haeri & Shrimpton 2012), 这里不再展开. 而非贴体类方法省去了网格更新过程的计算量, 同时背景的笛卡尔网格的简洁性使得流体相NS 方程求解过程中的一些快速算法得以应用. 这两点使得该方法的计算效率得到显著提升, 因而这类方法是目前模拟运动物体流固耦合 (如颗粒两相流) 问题的主流方法. 以下对非贴体类的浸没边界方法和格子-玻尔兹曼方法进行展开介绍. 由于虚拟边界法与浸没边界法思路相似, 这里不再展开描述, 相关详细过程可参考(Yu & Shao 2007b, 2010).

2.3.1 浸没边界方法

浸没边界方法最早是由Peskin 提出用来模拟心脏瓣膜流固耦合问题(Peskin 1972, 1977). 如图5 所示, 浸没边界法使用背景的欧拉网格和物体表面的拉格朗日网格分别描述流体和物体(Griffith & Patankar 2020). 对于流体-固体界面的边界条件, 该方法在NS 方程动量方程中施加一个额外的体积力项来实现, 即将原本NS 方程的动量方程修改为

图3全分辨颗粒两相流问题示意图

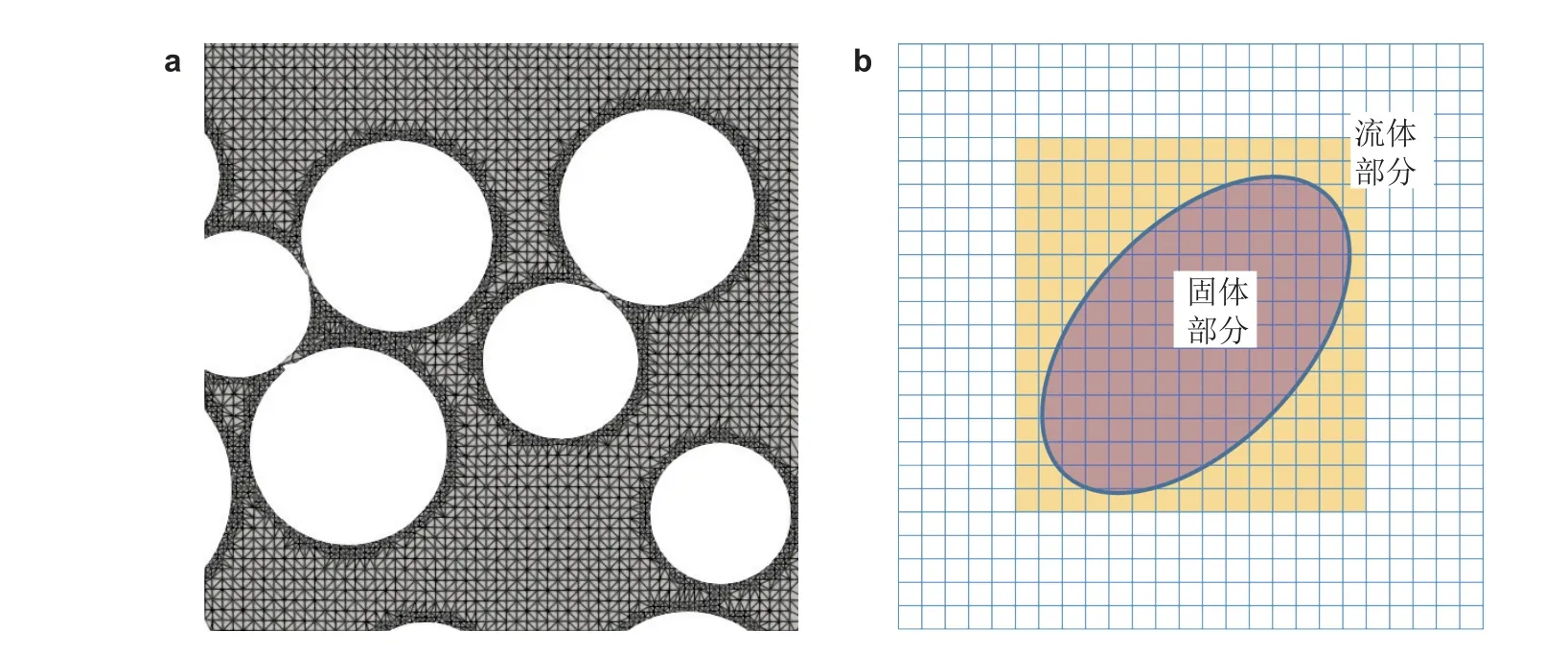
图4网格方法示意图. (a)贴体网格类方法, (b)非贴体类网格方法

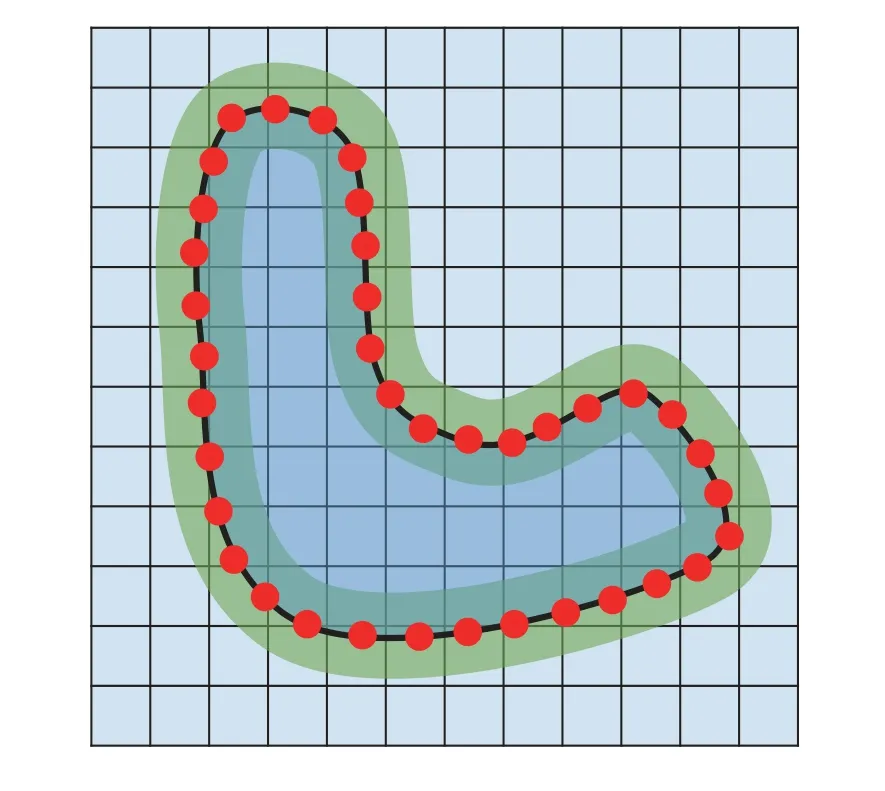
图5浸没边界方法的欧拉网格和拉格朗日网格

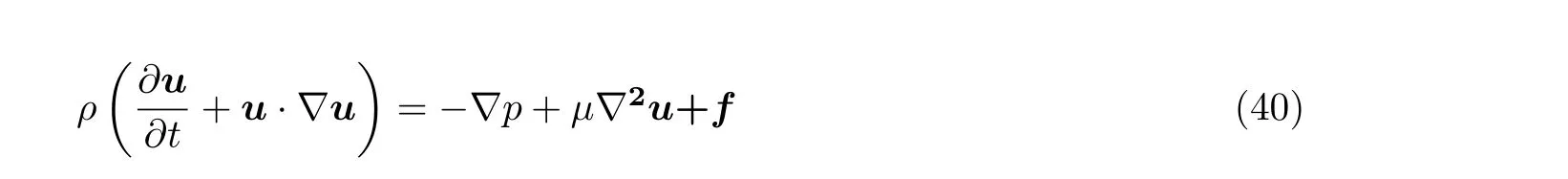
式中f称为浸没边界力 (IB 力) . 适当地施加IB 力后就可以使得流固无滑移边界条件即式(39)得到满足. 根据IB 力的施加方法, 浸没边界法可以分为两类, 即连续力法和离散力法(Mittal &Iaccarino 2005). 连续力法中的IB 力先在物体表面的拉格朗日网格上计算, 然后再通过离散的Delta 函数“传播”(spread)到背景欧拉网格上. 根据IB 力的具体计算方法, 这类方法包括Peskin 最早提出浸没边界法时的经典方法(Peskin 2002)、基于弹簧模型的方法(Lai & Peskin 2000)、罚函数法(Huang et al. 2011)、多孔介质模型法(Angot et al. 1999)、反馈力法(Goldstein et al. 1993)、直接力法(Uhlmann 2005)和投影法(Taira & Colonius 2007)等. 离散力法则是对没有IB 力的原始NS 方程先进行离散, 然后再根据流固界面边界条件在背景欧拉网格上直接施加IB 力. 这类方法又包含直接力法(Fadlun et al. 2000)、鬼点法(Majumdar et al. 2001)和切割网格法(Udaykumar et al. 1996)等. 连续力法中物体边界的识别是模糊的, 离散力法中边界的识别是清晰的, 但由于离散力法在处理运动物体时会由于边界位置改变导致插值过程不连续,进而导致虚拟的IB 力振荡(Mittal & Iaccarino 2005), 所以在处理颗粒两相流问题中, 通常使用连续力法. 这里以颗粒两相流全分辨模拟中广泛使用的直接力法(Uhlmann 2005, Breugem 2012)为例介绍浸没边界法的具体实施步骤.

首先对不施加IB 力的NS 方程动量方程进行离散得到预测速度u*

随后, 对颗粒的运动 (包括平动和转动) 利用颗粒动力学方程进行推进

通常, 对于非球形颗粒, 转动方程在颗粒参考系下求解, 详见2.1 节.

2.3.2 格子玻尔兹曼方法

格子玻尔兹曼方法 (lattice boltzmann method, LBM) 也是全分辨颗粒两相流问题数值模拟的有效手段. 格子玻尔兹曼方法本质上是一种流体求解器. 但是与传统的有限差分、有限体积等基于对描述宏观流体运动的NS 方程进行离散的流体求解器不同, 格子玻尔兹曼方法是从介观角度的气体动理学Boltzmann 方程出发来描述流体动力学(Chen & Doolen 1998), 即

方程(47)实际描述的是流体系统中“流体粒子”的运动, 式中的fi是流体粒子的在第i 个方向的速度分布函数,x代表“晶格” (lattice) 的位置,Ωi代表碰撞算子,i为晶格的方向指标 (通常对于二维问题可取9 个方向, 对于三维问题可取15,19 或27 个方向, 如图6 所示) , |ei|=dx/dt. 求解方程 (47) 涉及到“对流”(streaming)和“碰撞”(collision)两步, 常用Bhatnagar-Gross-Krook(BGK)单弛豫时间的碰撞算子(Chen et al. 1992, Qian et al. 1992)

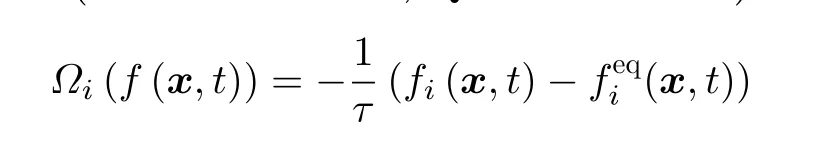
式中, 上标“eq”代表平衡态的分布函数, 具体形式可见参考文献(Chen & Doolen 1998). 得到方程 (47) 的解后, 对于不可压流动问题, 基于Chapman-Enskog 展开(Chen & Doolen 1998), 就可以得到流体力学中的宏观量 (如密度、压强、速度等) . 关于LBM 的具体求解步骤和推导过程,可以参见相关综述文章(Chen & Doolen 1998, Aidun & Clausen 2010)或相关书籍可参见 (何雅玲等 2009) .

LBM 方法较之于传统的方法有以下三个优点: 其一, 由于其求解过程局部性强, 求解过程简单 (无需求解微分方程) , 因此求解程序并行化容易, 并行效率高(Aidun & Clausen 2010). 其二,由于LBM 求解器是基于介观尺度的方法, 因此它不仅能够处理连续介质问题, 对于稀薄流动等连续介质假设失效的问题也可以进行模拟. 其三, 对于边界条件的处理也较容易, 例如可以使用回弹方法处理无滑移壁面(Ladd 1994a, 1994b), 使用Lees-Edwards 边界条件方法处理无界域内的剪切流动边界条件(Lees & Edwards 1972)等. 此外, 对于复杂流动问题 (如湍流、带界面的流动) 都可以使用基于LBM 的求解器进行处理(Aidun & Clausen 2010).

对于全分辨颗粒两相流问题, LBM 的回弹方法就可以直接地处理颗粒-流体边界处的无滑移条件(Ladd 1994a, 1994b), 并且可以通过计算碰撞过程中的动量交换求出颗粒受到的流体力和力矩(即FH,TH) , 从而用以推进颗粒运动的求解. 但是使用这种方法处理的颗粒边界呈台阶状(Tenneti & Subramaniam 2014), 并存在质量守恒无法满足、动边界力振荡以及伽利略不变性无法保证的问题(Aidun & Clausen 2010). 关于这些问题的讨论以及改进可以参看相关文献(Aidun &Clausen 2010, Peng et al. 2016).

图6格子结构与速度的示意图. (a) D2Q9, (b) D3Q19

2.3.3 浸没边界与格子玻尔兹曼混合方法

除了使用回弹模式处理颗粒-流体的边界之外, 也可以将LBM 流体求解器和浸没边界法相结合 (即LBM-IBM 方法) , 通过在颗粒表面处流体施加体积力的方法来满足无滑移边界条件.这种方法的好处在于既利用了LBM 求解器的易编程、易并行化的优点, 同时能够避免使用回弹方法带来的质量不守恒以及边界动量力振荡的问题(Aidun & Clausen 2010). 因此这种方法也被广泛应用于颗粒两相流全分辨数值模拟之中(Derksen 2011, Eshghinejadfard et al. 2016).

2.3.4 颗粒碰撞

对于全分辨的颗粒两相流模拟, 由于颗粒的尺寸不可忽略, 通常还要考虑颗粒之间的碰撞,即四向耦合. 当不考虑流体相时, 已经有相关综述文章详细讨论了非球形颗粒的碰撞问题 (称为干碰撞) , 并且对其中涉及到的接触检测和碰撞模型等重点问题进行了阐述(Zhong et al. 2016).但是当有流体存在时, 除了碰撞力, 颗粒间距很小时还存在润滑力作用. 即便是全分辨的数值模拟也无法分辨颗粒距离很近时的润滑力作用, 因此有流体存在时的颗粒碰撞 (称为湿碰撞) 更加复杂. 一般有三种思路对湿碰撞过程进行数值模拟. 最简单的是用简化的排斥力来模拟颗粒间的碰撞和相互作用Fip,j(Glowinski et al. 1999), 对于球形颗粒表达式为

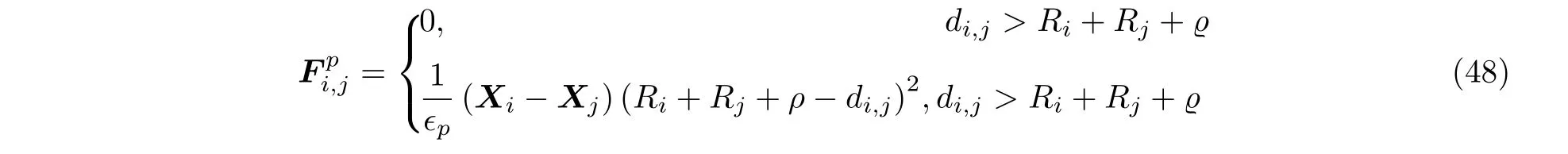
式中ϱ是碰撞力产生的阈值,ϵp ≪1 决定了碰撞力的大小, 这两个量均需要人为给定.di,j为两颗粒中心位置的距离,Ri与Rj分别为两颗粒半径,Xi与Xj分别为两颗粒的中心位置. 这种碰撞模型形式简单, 但是只能考虑法向碰撞力, 而且碰撞过程没有能量损失. 第二种思路是润滑力模型加硬球碰撞模型(Derksen 2011, Jain et al. 2019). 其中的润滑力模型是基于Jeffrey 对球形颗粒间润滑力的理论推导(Jeffrey 1982), 在颗粒间距小于一定范围 (通常是1 个欧拉网格) 时施加.而当颗粒相互接触之后, 再通过碰撞前两颗粒的速度、碰撞过程的动量守恒关系、和先验给定的恢复系数确定两颗粒碰后的速度大小. 这种方法不需要分辨颗粒接触后的碰撞过程, 理论上可以考虑法向和切向的动量交换, 但是对于多体碰撞 (三个或三个以上颗粒间的碰撞) 难以处理.最后一种思路是润滑力加软球碰撞模型(Xia et al. 2020). 这种思路同样在颗粒间距很近时首先施加润滑力作用, 而当颗粒产生相互接触后使用基于弹性力学理论推导得到的碰撞力 (例如经典的Hertz 模型) 来分辨碰撞过程. 这种方法与物理真实情况最为接近, 可以考虑碰撞过程的切向动量交换, 也可以考虑多体碰撞问题, 但是会由于碰撞过程刚度系数过大影响数值稳定性, 需要很小的时间步或用多时间步的方法来处理碰撞过程. 所以有些学者通过一种“人工延长碰撞时间”的方法减小碰撞过程的刚度, 从而改善碰撞模拟的数值稳定性(Kempe & Froehlich 2012,Costa et al. 2015).

3 非球形颗粒在静止流场沉降或均匀来流中转动

非球形颗粒在均匀来流中受到的力矩与其方位角的关系, 将决定其在均匀来流中的转动方式, 进而影响其在流体中的取向和受力. 影响非球形颗粒在均匀来流下的转动的关键无量纲数是颗粒雷诺数 . 本节将基于考虑不同Re的情况对该问题进行讨论, 并且以单个颗粒在静止流场中的沉降问题为例解释该问题的物理意义.

Re=U∞D/ν

3.1 Stokes 流动情况

当忽略流体惯性效应时, 根据Jeffery 的理论(Jeffery 1922), 在均匀来流中无论颗粒的方位角如何, 都不会受到流体力矩的作用, 也就是说颗粒会保持方位角不变. 根据这样的结论, 对于一个非球形颗粒, 以任意的初始方位角释放, 都会保持该角度不变. 而再根据非球形颗粒的受力公式(7), 就可以推导出颗粒以不同方位角沉降时的沉降速度(Ardekani et al. 2017a)

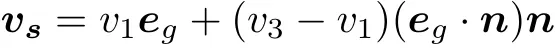
式中eg,n分别是重力方向和颗粒的回转轴方向单位矢量, 而v1,v3分别是回转轴与重力垂直和回转轴与重力平行时颗粒的沉降速度, 即对于细长颗粒v1对应最大阻力沉降速度,v3对应最小阻力沉降速度; 对于扁平颗粒则v1对应最小阻力沉降速度,v3对应最大阻力沉降速度. 也就是说,颗粒的沉降方位角、沉降速度矢量均可以不和重力方向重合, 颗粒以不同的取向沉降时也会有不同的沉降速度. Candelier 和Mehlig (2016)就利用细长体理论得到的颗粒受力表达式, 推导出一根细针 (如图7) 受重力作用沉降时, 速度矢量方向β和细针的取向角α的关系

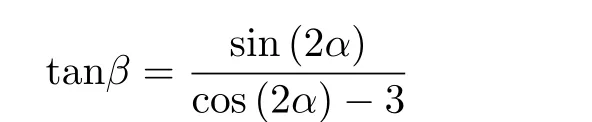
3.2 有限小Re 情况

图7细针以任意取向在流体中沉降示意图

在考虑流体惯性效应后, 结果会有显著的不同. Khyat 和Cox(1989)基于细长体近似理论,利用小参数渐进展开方法, 推导出了细长体 (κ=a/l ≪1 ) 在均匀来流中, 当κRe ≪1 时, 受到的力矩与取向角的关系. 随后Dabade 等(2015)给出了轴对称椭球颗粒的流体惯性力矩在有限小Re下 (Re ≪1 ) 的解析表达式式(23). 根据流体惯性力矩的形式与方位角的关系, 利用颗粒转动的稳定性分析, 可以推导放置在均匀来流中的颗粒, 在流体惯性力矩的作用下, 最终到达的平衡状态一定是阻力最大的取向方向.

对于沉降问题来说, 上述结论的推论就是, 以任意初始方位角释放的非球形颗粒, 即便在Re ≪1的情况下, 也不会像完全忽略流体惯性效应的Stokes 情况一样保持其方位角不变沉降,而是会在流体惯性的作用下逐渐改变姿态直至稳定到阻力最大的取向 (即细长颗粒回转轴和重力方向垂直, 扁平颗粒回转轴和重力方向平行) , 并且沉降速度矢量也会和重力方向平行, 沉降速度大小即前面所述的最大阻力沉降速度v1.

3.3 有限大Re 情况

尽管力矩系数的拟合公式定量上误差较大, 但是非球形颗粒在均匀来流中受到的力矩与其方位角的定性关系是明确的, 即随着回转轴和来流方向的夹角从0°增大到90°, 颗粒受到的力矩会先增大后减小. 并且如果颗粒可以自由转动, 最终稳定的取向将是阻力最大的方向(Ardekani et al. 2016). 当然如果雷诺数足够高, 使得颗粒后方出现周期性的涡脱落, 颗粒方位角将在其稳定取向方向附近振荡.

4 非球形颗粒在线性剪切流中的运动

4.1 颗粒中心处滑移速度为零

该部分的研究最早可以追溯到1922 年, Jeffery (1922)首先在Stokes 流中研究了椭球颗粒在简单线性剪切作用下的转动行为. Jeffery 认为忽略流体与颗粒的惯性时, 颗粒是处于不受外力的状态. 此时, 轴对称椭球颗粒在剪切流中的转动轨迹为稳定的封闭曲线, 又称Jeffery 轨迹. 该轨迹的形态与初始的颗粒取向有关. 如果椭球颗粒的三个主轴的长度均不相等, 椭球颗粒在线性剪切流中会呈现出复杂的运动状态, 而且在特定的形状参数下会呈现混沌的转动的行为(Hinch &Leal, 1979, Yarin et al. 1997), 如图8(b)～(d). Einarsson 等(2016)通过微槽道实验观察到颗粒因为轴对称的缺失引起的复杂的转动行为. 当考虑颗粒惯性且依然忽略流体惯性作用时, Lundell 和Carlsson(2010)与Challabotla 等(2015a)将Jeffery 力矩作为颗粒的合外力矩. 他们通过求解椭球颗粒的刚体转动的欧拉方程获得颗粒的转动行为, 他们发现杆状颗粒的回转轴倾向性地垂直于涡轴并在剪切平面内转动, 而碟状颗粒的回转轴的方向倾向朝着涡轴方向且绕着回转轴在剪切平面内转动, 且颗粒的转动形态随颗粒惯性的不同而呈现不同的取向轨迹线 (Lundell &Carlsson 2010, Challabotla et al. 2015a) 如图8(e)和图8(f). 对于三轴不等颗粒, Lundell(2011b)发现颗粒惯性会让颗粒从混沌的转动的状态转变为颗粒绕自身最短轴在剪切平面内周期转动的状态, 如图8(g). 为了进一步解释颗粒惯性与形状对颗粒行为的作用, Yarin 等(1997)最早使用了线性稳定性分析中的Floquet 理论研究了颗粒形状对转动行为的影响, 并发现趋近杆状的三轴不等颗粒的运动行为更容易出现不稳定转动的行为. Lundell (2011b)也通过Floquet 分析理论给出颗粒惯性对三轴不等颗粒的转动稳定性的影响. 而Einarsson 等(2014)对颗粒方程基于弱颗粒惯性进行摄动展开, 并利用Floquet 理论解析地得到轴对称椭球颗粒在弱颗粒惯性下自旋与翻转模态运动的稳定性. Cui Z 等(2019)系统地研究了轴对称与三轴不等椭球颗粒绕各个颗粒主轴方向转动的稳定性, 并从理论上提供了更加广泛的颗粒惯性与形状的参数下颗粒不同转动模态的稳定性. 与此同时, 当颗粒在简单线性剪切平面中进行准二维转动时, 不管颗粒形状与惯性如何变化, 颗粒均是周期转动. Lundell 和Carlsson (2010)发现颗粒的转动周期在颗粒惯性的临界值附近存在较大的阶跃, 当颗粒惯性远小于临界值时, 颗粒的转动周期只与形状有关但与惯性无关, 而在大于临界值时, 不同形状的颗粒转动周期均趋于相同值. 当流体的剪切形式随时间进行周期变化, 在特定的颗粒形状与惯性范围内, 轴对称椭球颗粒的转动也会呈现出混沌的运动现象(Nilsen et al. 2013).

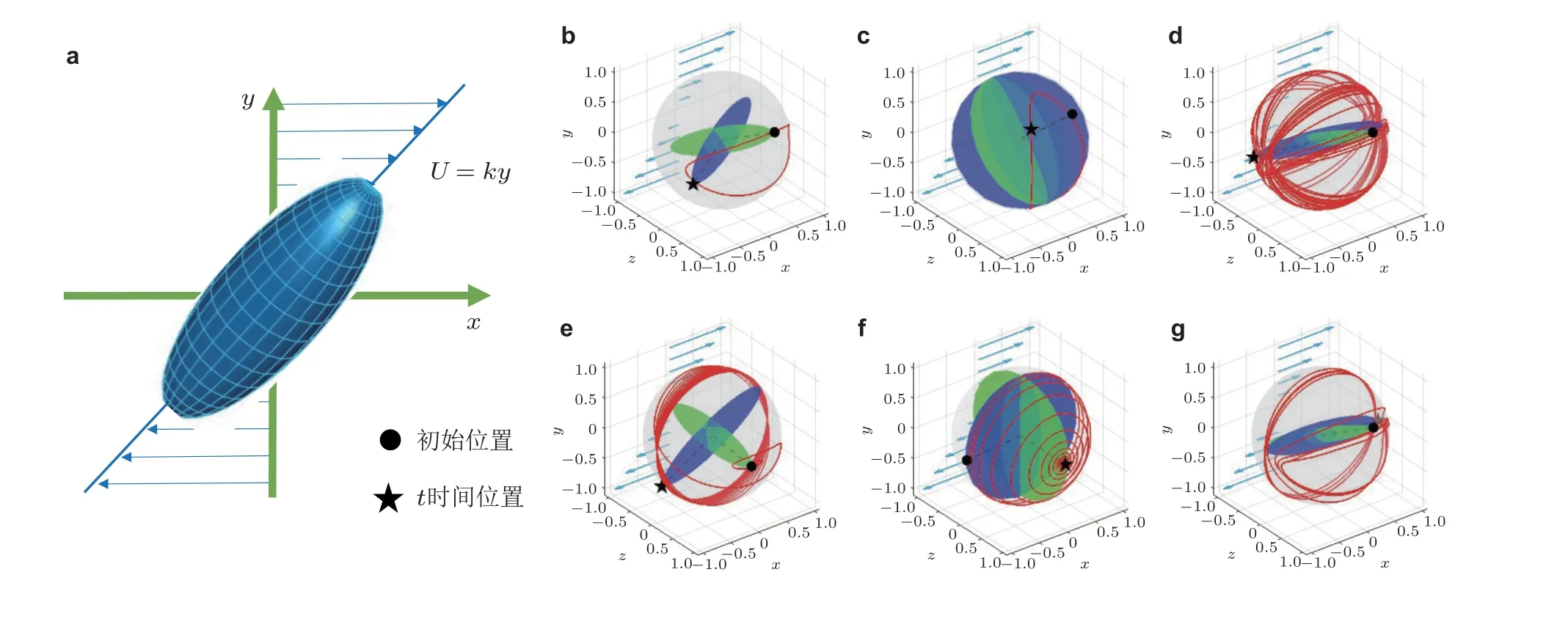
图8(a)颗粒在简单剪切流示意图; (b)～(g)椭球颗粒在剪切流中的转动时代表椭球颗粒方向的轨迹图. 其中(b)～(d)无惯性椭球颗粒, (e)～(g)以最长轴定义的颗粒转动惯性分布为 S tr =669, 646, 100 ;形 状 参 数(b)(e) λ =5 , (c)(f) λ =1/5 , (d)(g)ka =1,kb =10-0.65,kc =0.1

如果考虑流体惯性的影响, 非球形颗粒的转动将会变得更加复杂. Qi 和Luo (2002, 2003)较早利用格子玻尔兹曼方法研究了有限尺寸椭球颗粒在剪切流中的转动行为, 并发现随着颗粒雷诺数的增大以及颗粒形状的变化, 颗粒呈现出多种转动与取向模态. 随后, Yu 等(2007a), Huang等(2012) 以及Rosén 等 (2014) 进一步研究了轴对称椭球颗粒在剪切流中的行为, 发现并总结出在不同颗粒剪切雷诺数下椭球颗粒的不同运动模态 (如图9) , 随着颗粒惯性的增强, 杆状与碟状颗粒的运动模态发生变化. 表2 总结了长宽比为λ=2 和4 时杆状颗粒随颗粒剪切雷诺数变化时不同的运动模态. 表3 总结了长宽比λ=1/2 的碟状颗粒在不同雷诺数下的转动模态. Rosén 与其合作者(2015a, 2015b, 2016, 2017a, 2017b)进一步从定量角度深入探讨有限尺寸椭球颗粒在剪切流中的复杂行为 (包括不同模态以及模态之间的转换条件) , 并给出了定量研究的网格要求.他们发现颗粒惯性与流体惯性对颗粒转动行为的影响呈现出竞争的关系, 进而导致相同形状颗粒在不同初始位置下可能存在不同的转动行为. 同时, Rosén (2017a)发现了具有较大长宽比的杆状颗粒在流体惯性与颗粒惯性的相互作用下, 其自旋模态(回转轴与涡轴方向平行)可能会出现Shilnikov 分岔甚至混沌的行为. 当颗粒为三轴不等椭球颗粒时, 在极低颗粒雷诺数下三轴不等颗粒可能会出现混沌行为(Hinch & Leal 1979, Yarin et al. 1997, Lundell 2011, Cui Z et al.2019), Rosén 等 (2017b)较系统地研究了流体惯性对三轴不等椭球颗粒在剪切流中的运动行为.研究表明在流体惯性作用下三轴不等椭球颗粒的行为与极低雷诺数的情况下类似, 不过流体惯性会对颗粒绕中间轴的转动有一定稳定作用. 在理论研究方面, Meibohm 等(2016)通过摄动理论得到了轴对称椭球颗粒在自旋时的角速度随颗粒剪切雷诺数的关系. 而Dabade 等(2016)与Einarsson 等(2015)利用互等原理系统地研究在小剪切雷诺数下流体惯性对颗粒转动行为的影响.

图9颗粒在剪切流中转动的不同模态(Rosén et al. 2014)

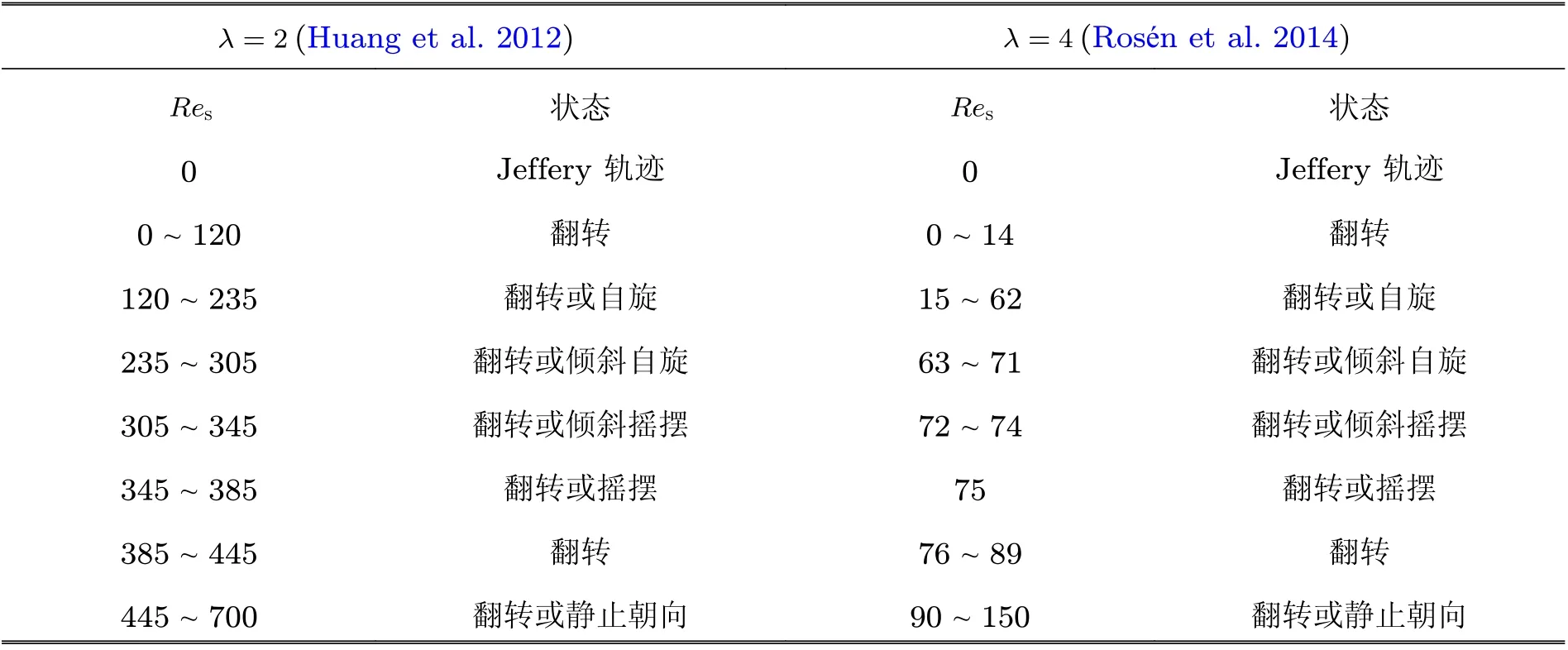
表2 有限尺寸杆状颗粒在剪切流中不同 R es 对应的转动模态

表3 有限尺寸碟状颗粒在剪切流中不同 R es 对应的转动模态

在Jeffery (1922)推导出椭球颗粒在Stokes 流中的力矩方程的同时, 也提出一个关于颗粒最终稳定转动状态应该处于系统最小能量耗散的猜想. Jeffery 认为杆状颗粒的回转轴平行于涡轴进行自旋和碟状颗粒的回转轴垂直于涡轴在速度梯度平面翻转为最终的稳定状态. 尽管Taylor(1923)通过实验观察颗粒转动的轨迹验证了Jeffery 提出的最小能量耗散的猜想, 但在近些年的直接数值模拟的结果中均不支持该猜想(Qi & Luo 2003, Rosén et al. 2014, Huang et al. 2012,Mao & Alexeev 2014). Huang 等 (2012) 的直接数值模拟的结果表明, 杆状颗粒的回转轴在速度梯度平面的翻转和碟状颗粒的回转轴平行于涡轴进行自旋是最终稳定的状态, 他们对应的是最大能量耗散的状态. Mao 和Alexeev (2014) 则发现对于长宽比为2 的杆状颗粒, 当颗粒剪切雷诺数大于60, 颗粒的转动会从翻转变为自旋模态. Einarsson 等 (2015) 通过摄动理论对颗粒运动方程基于小剪切雷诺数进行展开, 理论表明非常扁平的碟状颗粒的翻转与自旋在小剪切雷诺数下都可能是稳定的模态. 这些研究成果意味着Jeffery 提出的最小能量耗散的猜想可能存在一定的适用范围, 比如颗粒形状范围与颗粒剪切雷诺数范围等.

4.2 颗粒中心处滑移速度非零

对于大多数实际情况, 颗粒在流场中输运过程中一定会存在平动的滑移速度. 仅具有滑移速度的颗粒问题已经被大量的研究, 相关内容可以参见第3 节. 但同时考虑剪切与滑移的研究目前还缺少系统研究. Li 等(2019)研究了将颗粒中心固定在仅有一个壁面滑动的Couette 槽道流动的中心位置的转动情况. 其结果展示了椭球颗粒在平动滑移产生的流体惯性力矩与剪切产生的力矩作用下产生的转动行为, 但尚未对其运动行为展开系统与细致的深入研究工作(图10).

5 非球形颗粒在均匀各向同性湍流中的运动

均匀各向同性湍流是一种最简单的湍流场, 其各阶湍流统计特性在空间处处相等且不随坐标系的刚性转动而改变(张兆顺等 2017). 为了研究非球形颗粒与湍流的相互作用, 均匀各向同性湍流是一个比较合适的选择. 近些年, 有关非球形颗粒在均匀各向同性湍流中运动的研究比较活跃, 接下来将主要针对点颗粒与全分辨颗粒方法, 对目前的研究现状进行总结.

5.1 点颗粒椭球颗粒

5.1.1 无惯性椭球颗粒

图10颗粒中心处滑移速度非零时的剪切流模型示意图

对于颗粒尺寸远小于湍流的Kolmogorov 尺寸, 可忽略流体惯性以及颗粒惯性的作用. 此时颗粒轨迹可近似跟随流体质点, 颗粒的转动可以根据当地的流体速度梯度和颗粒取向信息通过Jeffery 方程求得, 而颗粒取向需要沿颗粒轨迹进行积分求得. 无惯性椭球颗粒因为其模型简单并且具有很好的跟随性而被广泛应用在非球形颗粒湍流的理论研究中. 尽管实际问题中颗粒惯性和流体惯性并不能完美与无惯性颗粒的假设符合, 但大量的实验观测结果表明, 无惯性椭球颗粒模型能较好预测微小颗粒(流体惯性和颗粒惯性影响非常小)的复杂行为 (Parsa et al. 2012,Marcus et al. 2014, Fries et al. 2017, Einarsson et al. 2016). Pumir 和Wilkinson (2011)和Ni 等(2014)报道了杆状颗粒的取向与流体的涡量方向具有强相关. 同时, 他们还发现杆状颗粒沿变形率张量的最大拉伸方向相关较弱, 但与变形率张量的第二特征方向相关反而较强. 但是颗粒取向与涡量的相关性主要在颗粒尺寸小于耗散尺度时较强. 如果颗粒尺寸超过流体的耗散尺度, 且在流体的惯性尺度的范畴, 那么杆状颗粒的取向是与变形率张量的最大拉伸方向相关最强(Pujara et al. 2019). 而对于碟状颗粒, 其回转轴倾向垂直于涡量方向, 且与变形率的最大压缩方向具有较强相关 (Gustavsson et al. 2014, Byron et al. 2015) . Ni 等(2014)发现杆状颗粒的取向与流体拉格朗日拉伸方向具有非常强的相关性. 他们认为长宽比大于10 的杆状颗粒与流体拉格朗日拉伸方向具有非常好的一致性. 与此同时, Zhao 等(2019b)发现颗粒的取向在空间的分布并不连续, 这意味着两个距离很近(小于Kolmogorov 尺寸)的颗粒依然存在大的夹角. 在颗粒转动方面, Parsa 等(2012)、Marcus 等(2014)和Byron 等(2015)通过实验和数值模拟得到了均匀各向同性湍流中颗粒翻转率(tumbling)与自旋率(spinning)随颗粒形状变化的函数关系 (如图11(a)所示) . 该图表明碟状颗粒的翻转率强于杆状颗粒, 但碟状颗粒的自旋率弱于杆状颗粒. 而当颗粒长宽比大于3 和小于1/3 时颗粒转动变化不明显. 然而, 在关于颗粒转动的前期的统计理论模型的研究中, 颗粒的转动行为对于碟状与杆状颗粒没有区别, 其转动率随颗粒形状的变化应该是基于λ=1 对称的(Shin & Koch 2005, Byron et al. 2015). 在该模型中, 湍流脉动随机且颗粒取向随机, 颗粒取向与流动相互独立. 而Parsa 等(2012)的工作从实验与数值上均说明了颗粒取向与流动结构的相关的重要性. Gustavsson 等 (2014) 从理论上解释在传统基于随机湍流的模型预测的颗粒行为与真实湍流中颗粒转动行为差异的原因. 他们认为碟状颗粒的持续翻转与颗粒轨迹经过高涡量区有关, 而传统的模型还不能捕捉. Pujara 等(2021)研究不同形状的颗粒的转动随着对直接数值模拟的湍流场过滤尺寸变化的关系. 研究结果表明无论用Kolmogorov 尺寸还是用积分尺度过滤流场, 颗粒的转动行为与颗粒形状的关系与过滤尺寸影响不大, 这表明非球形颗粒的转动可能体现了一种拉格朗日尺度的不变性. Chen 等(2016)发现目前的大涡模拟方法中流体相的亚格子模式对非球形颗粒的转动行为的影响较大, 使得其结构与直接数值模拟的结果具有较大偏差. 近日, Pujara 等(2021)提出的不同尺寸过滤后的拉格朗日尺度不变性可能会对非球形颗粒的亚格子模型的建立具有参考意义. 如果颗粒尺寸大于Kolmogorov 尺寸, Pujara 等(2019)发现杆状颗粒的翻转率与颗粒自身的长度满足-4/3 的幂律关系. 对于三轴不等颗粒, Chevillard 和Meneveau (2013)研究了三轴不等颗粒在各向同性湍流中的取向行为并与随机模型进行对比. Pujara & Variano (2017)研究了三轴不等椭球颗粒在各向同性湍流中的转动行为. 研究结果表明颗粒的拟涡能主要被分配给最长轴, 并且颗粒绕着其最长轴的转动是最持久的. 同时, 研究发现湍流中涡量-变形率的相关使得颗粒的总拟涡能与颗粒形状的关系较弱.

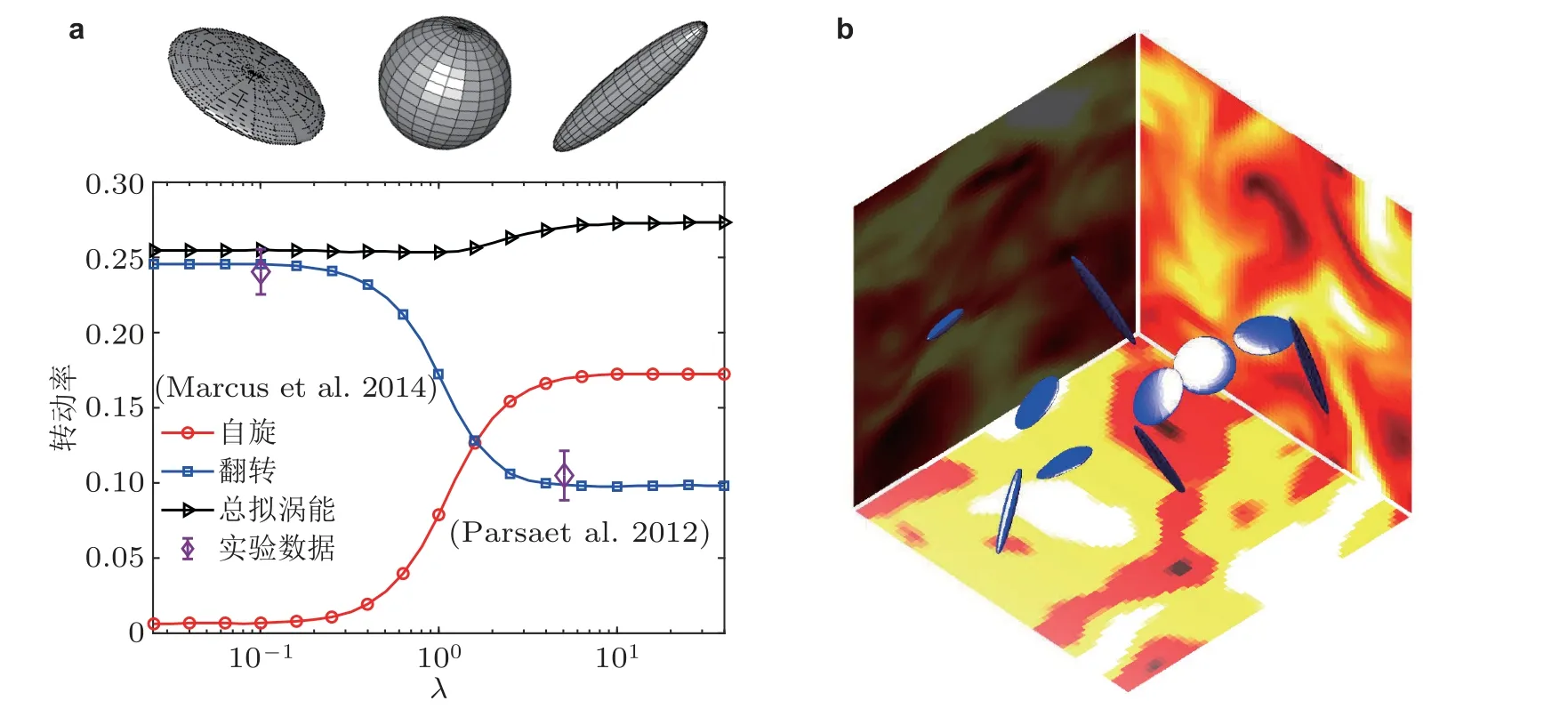
图11无惯性椭球颗粒的(a)转动率随形状变化的关系(数值模拟数据来自Byron 等 (2015), 两处实验数据分别来自Marcus 等 (2014)与Parsa 等(2012))与(b)在湍流中运动示意图

5.1.2 惯性椭球颗粒

当考虑颗粒惯性的作用时, 近期的实验发现, 纤维自身的惯性会降低纤维自身的转动(Bounoua et al. 2018). 然而, 非球形惯性颗粒在各向同性湍流的数值模拟研究却比较少. Roy 等(2018)仅研究了颗粒平动惯性对颗粒运动的影响, 却忽略了颗粒转动惯性的作用. 他们认为在各向同性湍流中非球形颗粒的转动弛豫时间要明显小于平动的弛豫时间. Zhao 等(2015)在槽道湍流的中部(流动趋近于各向同性湍流)研究了惯性非球形颗粒的转动行为随颗粒惯性的变化. 其结果也展示了颗粒惯性会削弱颗粒自身的转动行为. Gustavsson 等(2014)则是通过建立随机湍流模型研究了惯性非球形颗粒的转动行为. 关于颗粒惯性对颗粒在各向同性湍流中的取向与转动行为的影响依然缺少系统与深入的研究.

5.1.3 椭球颗粒沉降

在早期关于球形颗粒的沉降问题中, 湍流会加速颗粒的沉降(Maxey 1987, Wang & Maxey 1993, Bec et al. 2014). 这是因为重颗粒会倾向性地聚集在流动向下的区域(Wang & Maxey 1993, Bec et al. 2014). 对于非球形颗粒而言, 颗粒沉降的过程比球形颗粒的沉降更加复杂. 一方面是形状的各向异性导致沉降速度不仅与湍流强度有关还与颗粒取向有关(Siewert et al.2014a); 另一方面, 非球形颗粒的碰撞频率要比球形颗粒更加强烈(Siewert et al. 2014b). 为忽略颗粒惯性的影响, Ardekani 等(2017a)直接在无惯性颗粒的模型上添加了重力沉降速度. 其研究结果表明颗粒形状的增加会影响颗粒聚集以及平均的沉降速度. 其背后可能的原因有两个: 一个是形状对颗粒转动的影响, 另一个是提高了阻力的各向异性, 而前者的作用更加明显. Jucha 等(2018) 通过研究碟状颗粒的沉降过程时发现在湍流能量耗散率较小时颗粒的碰撞主要由相邻颗粒的取向差异引起的重力沉降导致. 随着湍流能量耗散率的增加, 湍流的脉动主要诱导了颗粒的碰撞行为. Gustavsson 等(2017)利用简单的高斯随机模型就准确预测了非球形重颗粒在湍流中的取向行为.

随着Dabade 等(2015)推导出轴对称椭球颗粒流体惯性力矩的解析表达式, Gustavsson 等(2019)、Sheikh 等(2020) 和Anand 等(2020)意识到流体惯性力矩在非球形颗粒在湍流中沉降的重要性. 流体惯性力矩主要由颗粒与流场的滑移速度诱导, Gustavsson 等(2019)发现当Rep ≪1时, 流体惯性力矩的作用依然不可忽略. Sheikh 等(2020)引入无量纲参数 ℜ 衡量流体惯性力矩与黏性力矩. 当 ℜ≫1 时, 颗粒倾向朝着阻力最大的方向进行沉降.

5.2 有限尺寸颗粒

而在各向同性湍流中进行全分辨颗粒的模拟的研究到目前为止依然比较少. Schneiders 等(2017, 2019)在各向湍流中研究了尺寸接近流体Kolmogorov 尺寸的非球形颗粒运动行为以及颗粒与流体之间的相互作用, 并与传统的拉格朗日双向耦合点颗粒模型进行比较(图12). 结果表明非球形点颗粒模型在预测取向行为上的准确性, 但在颗粒速度、颗粒与流场的相互作用等方面依然还存在明显差距. 如何基于全分辨颗粒的研究结果去改进拉格朗日点颗粒模型在未来依然是一个值得研究的方向.

6 非球形颗粒在壁湍流中的运动

在实际工程问题中, 湍流具有各向异性且在空间上分布不均匀. 壁湍流就是一种典型的强剪切和强各向异性的湍流模型. 由于壁面的存在, 在壁面附近不仅存在强的速度剪切, 而且还存在非常丰富的湍流结构, 比如流向涡、条带、猝发等(许春晓 2015). 随着雷诺数的升高, 壁湍流的外区存在大尺度结构, 这些大尺度结构的流向长度通常为2～3 倍、13～15 倍甚至20 倍外区尺度(许春晓 2015). Zhang 等(2001)最早在壁湍流中进行非球形颗粒两相流的直接数值模拟研究, 随后研究学者们陆续在壁湍流中展开了全方面的非球形颗粒两相流研究. 目前对非球形颗粒在壁湍流的运动行为特征有了基本的认识. 本节围绕近些年关于非球形颗粒在壁湍流运动的研究进展展开讨论.

6.1 点颗粒椭球颗粒

6.1.1 无惯性椭球颗粒

图12有限尺寸杆状颗粒在湍流中分布示意图(a)与(b)自适应网格加密(Schneiders et al. 2019)

由于壁面的存在, 壁面附近的流动呈现出明显的各向异性与不均匀性的特点. Challabotla等(2015b) 最早研究了无惯性椭球颗粒在槽道湍流中的取向行为. 在近壁面附近, 杆状颗粒的回转轴方向倾向朝着流向方向, 而碟状颗粒的回转轴倾向指向壁面的法向方向(如图13(a)(b)).但在远离壁面的槽道中部附近, 颗粒的取向行为趋于同颗粒在各向同性湍流中的行为类似, 这是因为在槽道中部的湍流具有局部各向同性的特性(Andersson et al. 2015). 同时, 近壁面附近存在复杂的湍流相干结构, Cui Z 等(2021)首次观察到非球形颗粒取向与流向涡结构、上抛和下扫事件以及速度条带之间的相关, 并提出颗粒的取向行为在近壁面附近可以被定性地划分为剪切主导区、结构主导区以及各向同性区(如图14). 在剪切主导区, 颗粒在强剪切的作用下其旋转会受到抑制, 杆状颗粒与碟状颗粒会在特定的朝向停留较长时间 (Challabotla et al. 2015b, Zhao et al. 2015) . 逐渐远离壁面, 流场的剪切减弱, 湍流结构增加, 进入结构主导区域. 此时, 杆状颗粒与碟状颗粒均会受到结构的影响, 进而使得颗粒在流向涡周围、上抛与下扫事件中以及高低速条带中的取向行为产生明显差异(Cui Z et al. 2021). 该类似现象在早期的实验中也得到了观察, 即杆状颗粒在高速条带中取向相对随机而在低速条带取向更趋近于流向方向(Abbasi Hoseini et al. 2015). 但是该工作将此现象简单地归结为颗粒与壁面碰撞的有限尺寸的影响, 并未深入分析和探讨背后的原因. 而Cui Z 等(2021)的工作已经消除了潜在的颗粒与壁面之间由于颗粒有限尺寸导致的碰撞效应的影响. 当颗粒位置进一步远离壁面, 剪切趋近于零, 而湍流也趋于各向同性, 此时颗粒的转动与取向行为逐渐与其在各向同性湍流中的行为类似(Zhao et al.2015). 不过, 在中高等雷诺数槽道湍流中, 由于流场中存在大尺度结构(比如等动量区与非等动量区), Jie 等(2019)发现等动量区的内外颗粒的转动统计行为存在明显差异, 图15 展示了Reτ=1000槽道湍流中杆状颗粒的取向分布瞬时图.

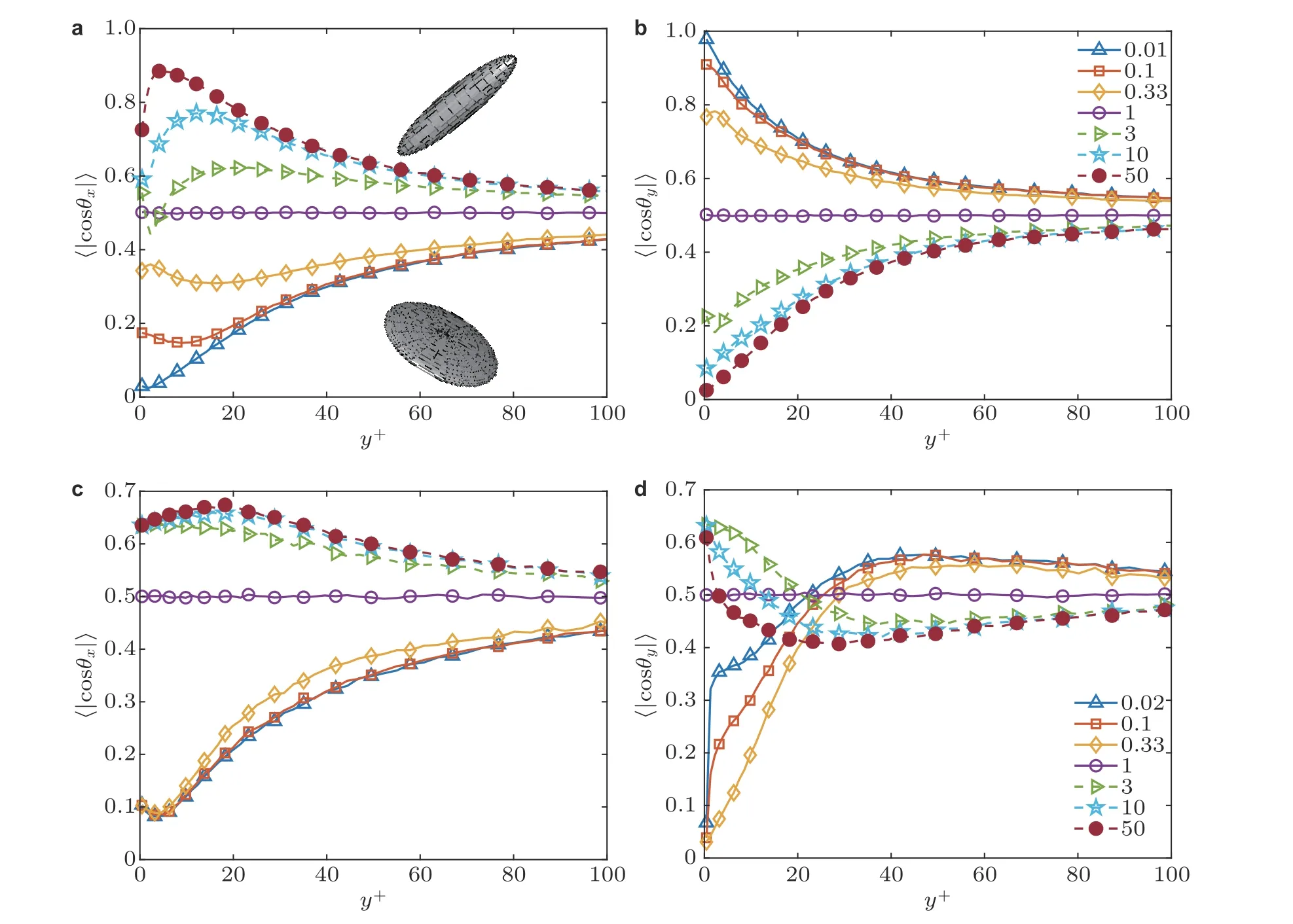
图13椭球颗粒在槽道湍流中的取向分布. (a)(b)无惯性椭球颗粒(Challabotla et al. 2015b); (c)(d)St =30 椭球颗粒

同时, 由于壁面剪切的存在, 杆状颗粒与碟状颗粒在近壁面附近的取向均与流体的涡量方向接近垂直 (Zhao et al. 2015) . Zhao 和Andersson (2016)发现杆状颗粒与碟状颗粒分别与流体拉格朗日的拉伸与压缩方向有关, 但相关程度并没有其在各向同性湍流中强. Cui Z 等(2020)进一步研究了杆状颗粒的取向与流体拉格朗日拉伸方向的相关, 并发现Ni 等(2014)提出的长宽比大于10 的杆状颗粒与流体拉格朗日拉伸方向一致的结论在槽道中并不是处处成立. Cui Z 等(2020)发现长宽比大于10 的杆状颗粒行为与流体拉格朗日拉伸方向在黏性底层存在明显差异.以图16 为例, 其展示了长宽比为23.3 的杆状颗粒与流体拉格朗日拉伸方向沿同一条颗粒轨迹线的取向行为. 图16 的结果显示流体拉格朗日拉伸方向在靠近上壁面时主要朝着流向方向而杆状颗粒在壁面附近持续翻转. Cui Z 等(2020)认为这一现象主要与近壁面的速度剪切和速度梯度脉动有关. 当考虑三轴不等颗粒时, Challabotla 等(2016a)发现颗粒同时具有碟状与杆状颗粒的特性, 即颗粒像杆状颗粒一样绕着最长轴转动也像碟状颗粒一样绕着最短轴转动.

如果壁面剪切趋于零, Yang 等(2018)通过构造Couette-Poiseuille 流动发现无惯性的杆状颗粒在零剪切壁面附近取向趋向随机而碟状颗粒依然指向壁面法向. 同时, 他们的研究结果还表明颗粒的各向异性的转动模态主要与颗粒取向的各向异性有关, 而壁面平均剪切对转动模态的影响起次要作用.

6.1.2 惯性椭球颗粒

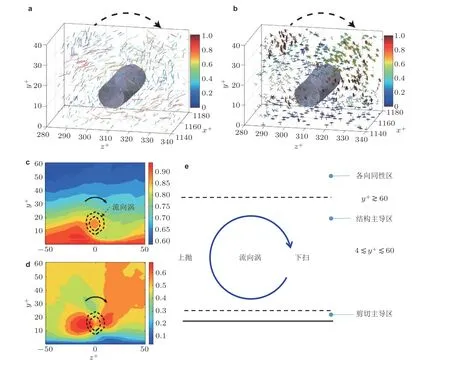
图14颗粒在近壁流向涡结构影响下的取向行为及区域划分(Cui Z et al. 2021). (a)(b)分别为细长杆状与扁平颗粒在瞬时流向涡附近的取向分布; (c)(d)条件系综平均后的颗粒取向分布, 其中(c)细长杆状颗粒与流向夹角余弦值 | cosθx| ; (d) 扁平颗粒与展向夹角余弦值 | cosθz| ; (e)依据颗粒取向行为特点进行的区域划分示意图

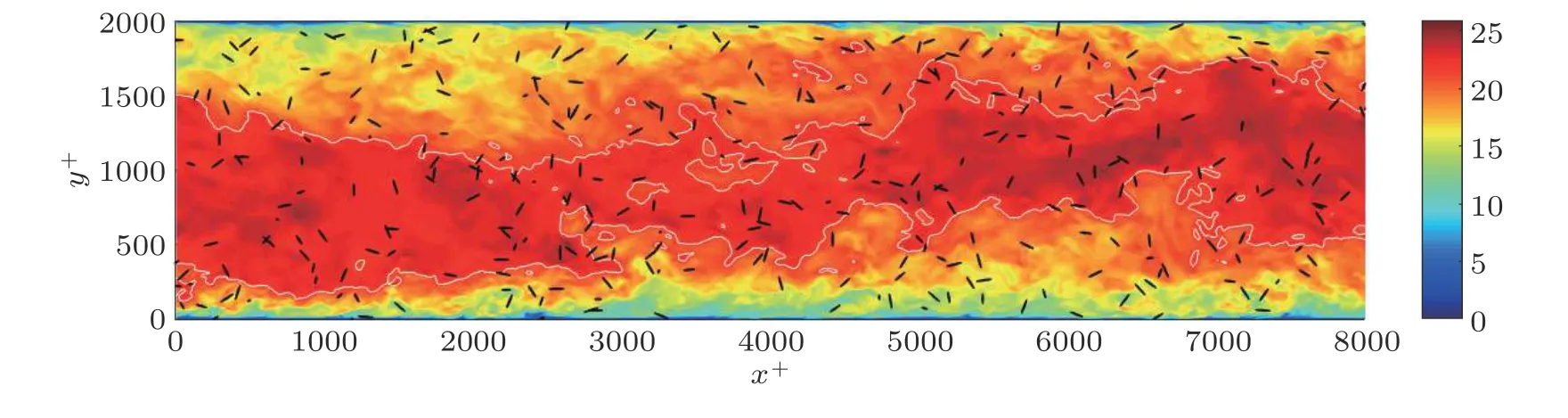
图15杆状颗粒在雷诺数 R eτ =1000 槽道湍流分布图. 其中云图为流向速度, 白色等值线代表0.95 倍槽流中心平均速度

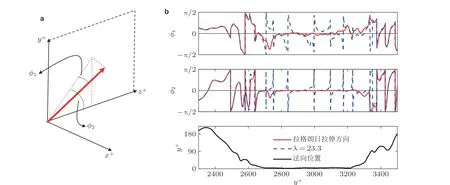
图16无惯性杆状颗粒在壁面取向行为与流体拉格朗日拉伸方向的差异(Cui Z et al. 2020)

在壁湍流中, 考虑颗粒惯性的研究要早于无惯性颗粒的研究, Zhang 等(2001)最早实现了壁湍流中惯性杆状颗粒的输运与沉积特性. 随后, Mortensen 等(2008a, 2008b)、Marchioli 等(2010,2013, 2016)、Zhao 等(2013, 2014, 2015)、Challabotla 等(2015c)和Yuan 等(2018)的研究表明惯性椭球颗粒倾向性地聚集在低速度条带, 且与颗粒形状的影响较小, 这与惯性球形颗粒的输运特性类似. 然而颗粒的转动与取向行为依赖颗粒形状. 对于杆状颗粒, 随着颗粒长宽比的增大,杆状颗粒在近壁面倾向朝着流向方向, 但随着颗粒惯性的增大, 倾向性取向行为减弱, 进而杆状颗粒倾向在强剪切平面内翻滚地向下游输运. 对于碟状颗粒, 随着颗粒非球形度的增大, 弱惯性的碟状颗粒在近壁面倾向朝着壁面法向, 但随着颗粒惯性的增大, 碟状颗粒像车轮一样在壁面滚动着向下游输运. Zhao 等(2014)与Marchioli 等(2016)分别研究了杆状颗粒与流场之间平动滑移速度与转动滑移角速度随颗粒惯性与形状的影响. 其结果表明随着惯性逐渐趋近于零, 颗粒与流场之间的转动滑移角速度并不像平动滑移速度那样趋近于零, 依然存在明显的滑移角速度.Zhao 等(2015)对槽道湍流中惯性椭球颗粒的转动进行分析, 发现壁湍流中的近壁转动模态与远离壁面的转动模态是完全不同的. 在远离壁面的转动模态, 碟状颗粒倾向绕非回转轴垂直于涡量方向进行翻转, 而杆状颗粒绕回转轴沿涡量方向自旋. 随着颗粒惯性的增大, 这种趋势被削弱.然而在近壁区域, 颗粒的惯性反而增加了碟状颗粒绕回转轴在剪切平面转动而杆状颗粒绕非回转轴转动. 进一步, Zhao 等(2019a)系统研究轴对称椭球颗粒在槽道不同高度时的转动模态随剪切、湍流强度与颗粒惯性的影响, 并研究了从壁面到槽道中部两种转动模态的转变. 最近,Michel 和Arcen (2021a)的研究表明非球形颗粒的统计量需要较长的时间才能统计稳定, 同时,Marchioli 等(2016)的报道表明颗粒的转动和取向行为比平动的统计更快统计稳定. Michel 和Arcen (2021b)研究了不同槽道湍流的雷诺数(从Reτ=180 到550)对惯性杆状颗粒的行为进行研究. 其结果表明随着雷诺数的增大, 颗粒在壁面的倾向性取向与转动行为有轻微的减弱.

6.1.3 重力沉降考虑重力沉降时, 目前大部分相关研究中主要考虑重力方向与槽道流向平行的情况, 即竖直槽道. 当槽道流动方向与重力方向一致, 称为向下流动的竖直槽道, 当流动方向与重力相反, 则称为向上流动的竖直槽道, 如图17. Challabotla 等(2016b, 2016c)和Yuan 等(2017)的研究表明重力会影响到颗粒的聚集形态, 使得颗粒有显著的法向输运. 当流动方向向上时, 非球形颗粒的分布会更加均匀, 而流动方向向下时, 颗粒聚集十分明显, 而该影响随着颗粒惯性的增大而减弱,且与颗粒形状的关系不大. 除了非常靠近壁面的位置, 重力并不会对颗粒的取向与转动行为有明显的影响. Yuan 等(2018)进一步发现重力的作用会影响湍泳聚集(Turbophoresis)的机制且使得远离壁面的运动颗粒比靠近壁面的运动颗粒更聚集在流体的低速条带. 如果忽略颗粒惯性的作用, Qiu 等(2019)发现的非球形颗粒在向上流动的竖直槽道中倾向聚集在壁面, 而在向下流动的竖直槽道中倾向聚集在槽道中部. 这说明, 如果重力作用与基于湍泳机制聚集的作用相反, 那么颗粒的分布将会趋于均匀 (即向下流动情况) ; 如果两种作用相同, 那么会增强颗粒在壁面的聚集(即向上流动情况). 而重力方向导致不同的法向输运特点可能与壁面附近的流动上抛与下扫事件以及流动结构相关. 其具体的影响值得进一步深入研究.

6.2 有限尺寸颗粒

Do-Quang 等(2014) 对惯性较小的纤维使用全分辨方法研究其在槽道湍流中的行为, 并发现纤维会因为其与壁面的碰撞效应而倾向性的聚集在高速条带, 且较长的纤维在槽道中部有朝着展向的趋势, 随着逐渐靠近壁面, 较长的纤维在逐渐在剪切平面内转动. 而在壁面附近纤维主要朝着流向方向. Eshghinejadfard 等(2017, 2018)以及Zhu 等(2018)进一步研究了中性悬浮杆状与碟状颗粒在槽道中的行为以及其与流体的相互作用. 他们发现在缓冲区时, 颗粒的运动速度要快于流体速度, 且杆状颗粒倾向性朝着流向而碟状颗粒倾向性地朝着壁面法向. 而在远离壁面的位置, 颗粒的取向又趋于各向同性, 这与点颗粒方法得到的结论类似. Eshghinejadfard 等(2019)通过改变颗粒与流体的密度比来改变颗粒的惯性, 其研究结果表明颗粒与流体间的密度比增大会影响流体与颗粒的统计行为. 其中颗粒的取向统计行为与点颗粒类似, 随着颗粒惯性的增大(密度比增加), 杆状颗粒与流向、碟状颗粒与法向的取向行为被削弱. Zhu 等(2020)研究轴对称杆状颗粒与碟状颗粒在竖直向上流动的槽道湍流中的沉降问题. 其结果显示沉降的颗粒倾向于朝槽道中部迁移, 这种效应对于球形颗粒最明显. 而非球形颗粒在近壁附近依然使其最长轴沿流向方向, 但在槽道中部由于沉降作用呈现出垂直流向的关系. 同时, Zhu 等(2020)还发现颗粒倾向性会聚集在高速条带.

7 颗粒取向与转动行为的力学机理

非球形颗粒尽管外形各向异性, 但是对于大部分问题中颗粒的聚集行为与颗粒形状关系不明显, 聚集的机理基本可以由湍流泳动的机制以及近壁相干结构进行解释. 本文将主要讨论由于形状各向异性导致的复杂颗粒取向与转动行为背后的机理.

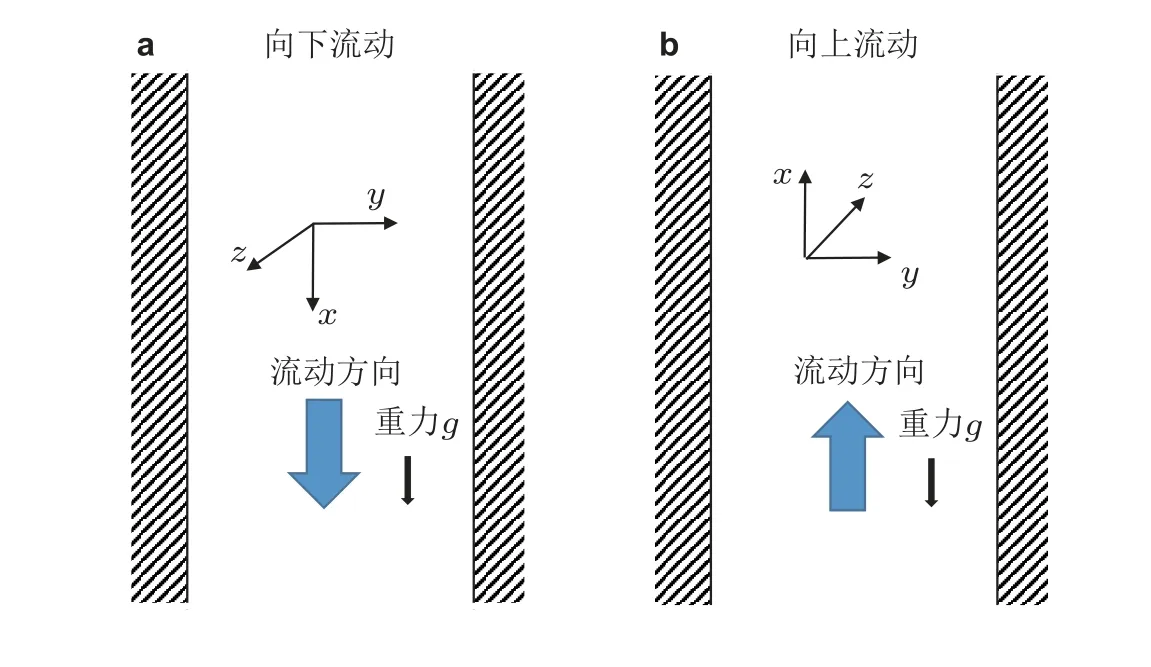
图17竖直槽道示意图.(a)向下流动, (b)向上流动

7.1 涡量与变形率张量的影响

目前, 一些工作尝试解释各向同性湍流和壁湍流中的颗粒复杂行为的力学机理, 其中有关颗粒行为与涡量以及变形率张量的第二主轴的研究较为普遍(Pumir & Wilkinson 2011, Parsa et al. 2012, Byron et al. 2015). 比如, 在均匀各向同性湍流中, 无惯性的杆状颗粒与流体的涡量方向具有较强的一致, 而碟状颗粒垂直于涡量方向(Pumir & Wilkinson 2011, Byron et al. 2015).Pumir 和Wilkinson(2011)认为杆状颗粒之所以与涡量方向一样, 是因为涡量方向的演化方程与杆状颗粒的运动方程具有类似性, 其中涡量方向的方程只比杆状颗粒取向方程多了额外的黏性扩散项. 因为杆状颗粒与涡量方向的关系, 在统计意义上杆状颗粒的绕回转轴转动的速率(Spinning)要强于碟状颗粒, 但杆状颗粒翻转速率(Tumbling)要弱于碟状颗粒(Parsa et al. 2012,Marcus et al. 2014, Gustavsson et al. 2014, Byron et al. 2015). 不过, 直觉认为杆状颗粒应该更加倾向性地朝着当地的变形率张量的最大拉伸方向. 然而, 学者们(Pumir & Wilkinson 2011, Gustavsson et al. 2014, Guala et al. 2005, Chevillard et al. 2013, Ni et al. 2014)却发现杆状颗粒和流体涡量并不会朝着变形率张量的最大主轴方向. 相反, 杆状颗粒与流体涡量与变形率张量的第二特征向量相关较强. Xu 等(2011)发现并提出涡量会跟随变形率张量的最大拉伸方向变化, 但是当涡量转动到相应位置时, 原来的流体变形率张量的主轴方向已经随流体转到其他方向. 在壁湍流中, 壁面附近的强剪切的使得壁面处的涡量方向一直朝着壁面展向方向, 但是无惯性杆状颗粒与碟状颗粒的回转轴方向却分别倾向性地朝着流向与壁面法向方向, 与涡量方向的夹角均接近直角, 如图18(a)所示. 如果考虑颗粒惯性, 壁面的强涡量给颗粒提供了持续不断的能量, 颗粒为了维持稳定, 在自身转动惯量的作用下, 杆状颗粒与碟状颗粒的转动均倾向性地在流向与法向平面转动(Zhao et al. 2015, 2019). 此时, 在颗粒惯性的作用下, 杆状颗粒垂直于涡量但碟状颗粒回转轴却与涡量对齐(Zhao et al. 2015, 2019), 如图18(b). 但是, 因为在槽道中部槽道中部的湍流趋近于均匀各向同性的湍流的流动特征(Andersson et al. 2015), 颗粒的取向规律基本与各向同性湍流中的相同(Zhao et al. 2015, 2019).

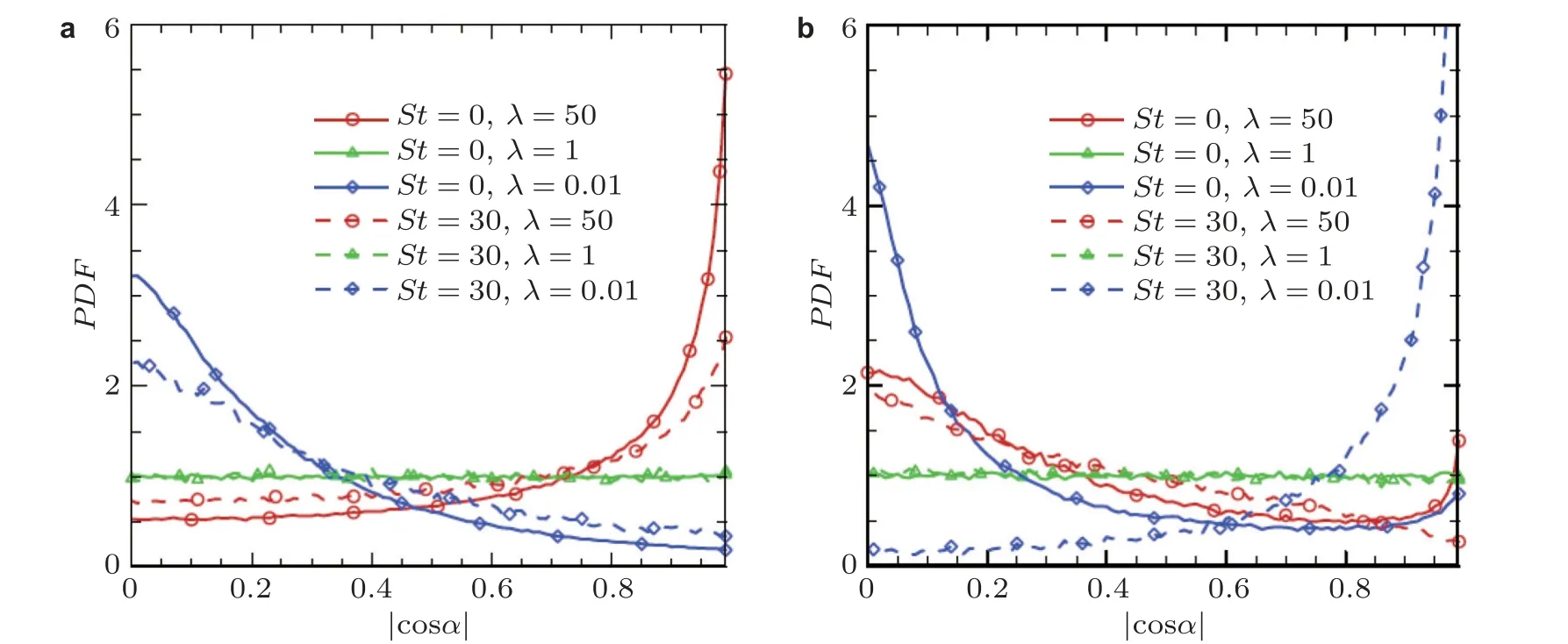
图18不同形状和颗粒惯性的非球形颗粒回转轴方向与涡量的夹角分布(Zhao et al. 2015). (a)槽道中部, (b)近壁区

由此得知, 颗粒取向行为与涡量和变形率的统计关系并不具备普适性, 比如, 杆状颗粒倾向性朝着涡量方向仅在槽道中部或者均匀各向同性湍流中成立, 但在各向异性的近壁湍流附近杆状颗粒却与涡量方向垂直(Zhao et al. 2015). 而且, 颗粒在二维湍流或准二维流动中均不存在上述关系, 因为在二维流动中涡量始终垂直于二维平面.

7.2 拉格朗日结构

无论是分析颗粒取向与流体涡量以及变形率张量的关系, 还是颗粒取向与标量梯度存在的联系, 这些研究均考虑颗粒取向与欧拉观点下的流场物理量进行的比较分析. 实际上, 对于颗粒而言, 其方程均在拉格朗日观点下进行点颗粒追踪求解. 对于无惯性的微小椭球颗粒, 颗粒轨迹就是流体迹线, 而颗粒的转动可以由当地的速度梯度信息与Jeffery 方程直接得到. 如果仅采用颗粒与欧拉物理量(比如涡量与变形率张量) 进行比较, 将得到的是颗粒与瞬时的欧拉流场的关系, 其并不能真实反映颗粒的拉格朗日行为特性.

如何从拉格朗日观点研究颗粒与流体拉格朗日量进行比较？在拉格朗日观点下, 一个初始是球形的流体微团沿着流体轨迹线会发生拉伸变形, 其中最强拉伸与压缩方向可以被认为是流体拉格朗日的拉伸与压缩方向(Ni et al. 2014, Zhao & Andersson 2016). Parsa 等(2011)则通过实验数据获得杆状颗粒与流体拉格朗日拉伸方向之间存在明显关系, 并展示了流体拉格朗日拉伸结构对杆状颗粒取向行为的影响 (如图19(a)(b)).

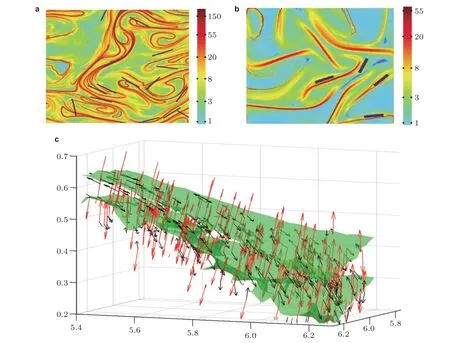
图19纤维与拉格朗日拉伸结构的关系. (a)周期流动(Parsa et al. 2011), (b)非周期流动(Parsa et al.2011), (c)拉格朗日拉伸(黑色箭头)与压缩(红色箭头)与拉格朗日结构的关系(Cui Z & Zhao 2021)

流体拉格朗日拉伸与杆状颗粒取向存在怎样的关系呢? 如果考虑一个细长杆状颗粒, 其可以被近似地认为是一个物质线段, 其方向与流体拉格朗日拉伸方向渐近一致(Pumir et al. 2011,Parsa et al. 2012, Batchelor 1952, Johnson et al. 2017). 在早期研究工作就发现物质线段方向以及流体拉格朗日的拉伸方向就与涡量以及变形率张量的第二特征值方向有较强的关系(Girimaji& Pope 1990, Guala et al. 2005). 杆状颗粒与拉格朗日拉伸方向以及物质线段存在一些差别, 比如杆状颗粒始终是有限长宽比, 且不会在流体作用下发生拉伸与压缩的变形. Ni 等(2014)验证了杆状颗粒(长宽比大于10)的取向可以用流体拉格朗日拉伸方向近似替代. 与此同时, Zhao 和Andersson(2016)的研究结果也发现在槽道湍流中颗粒的朝向与Ni 等(2014)在各向同性湍流中的结论类似, 即细长杆状颗粒的取向与流体拉格朗日最大拉伸方向有关, 而扁平碟状颗粒取向与流体拉格朗日最大压缩方向相关. 但是, Cui Z 等(2020)的研究表明颗粒形状(长宽比大于10)依然会对槽道的近壁附近的杆状颗粒取向行为产生显著影响. 而产生这一现象的原因可以归结为槽道不同位置处流场的平均剪切与速度梯度脉动强度的比值较大. 如果考虑杆状颗粒在流体拉格朗日拉伸与压缩方向组成的坐标系中的取向分布, Cui Z 等(2020)的工作表明无论在壁面附近还是在槽道中部不同形状的杆状颗粒的取向分布均存在一个平台区和幂律接近-2 的尾部区.平台区的存在就意味着颗粒在该区间内取向分布相对均匀, 对应着颗粒取向与流体拉格朗日拉伸方向的差别. 越靠近壁面, 平台区的范围更大, 颗粒取向与流体拉格朗日拉伸方向的差别就更明显.类似的平台与幂律区的分布也意味着杆状颗粒与流体拉格朗日拉伸方向的关系在全场是类似的. 不过, 越靠近壁面, 流场的平均剪切与速度梯度脉动的比值变大, 分布函数中的平台区变宽, 杆状颗粒与流体拉格朗日拉伸方向的差别就变得更加显著. Ni 等(2014)、Zhao 和Andersson (2016)以及Cui Z 等(2020)的研究均说明了一个共同的规律, 即随着长宽比的增加/趋于零, 杆状/碟状颗粒逐渐与流体拉格朗日拉伸/压缩方向一致. 只不过在剪切湍流中, 若想让颗粒与流体拉格朗日方向完全一致, 则需要更小的形状差异δΛ=1-|Λ| . 有关这一部分的阐述可见崔智文和赵立豪(2021)关于该内容的详细综述.

随着人们对无惯性椭球颗粒取向行为研究的深入, 流体的拉格朗日拉伸与压缩方向与非球形颗粒取向之间的数学关系也逐渐明晰. 在Pumir 等(2011)、Ni 等(2014)以及Cui Z 等(2020,2021)的工作中均将Jeffery 方程中的Λ=1 或 - 1 去近似替代流体拉格朗日拉伸或压缩以及细长的杆状或扁平的碟状颗粒. 其背后的数学关系可以由Batchelor (1952)无限小物质线与物质面的演化得到. 不过 Balkovsky 和Fouxon (1999)的工作发现当积分时间足够长后左柯西格林张量的最大与最小的特征向量(即流体拉格朗日拉伸与压缩方向)的方程形式与Jeffery 方程中令Λ=1或 - 1 一样. Cui Z 和Zhao (2021)则在该工作的基础上, 进一步推导并完善了左柯西格林张量特征方向的时间演化方程, 并发现其在数学形式上与无惯性三轴不等椭球颗粒主轴的时间演化方程的高度相似性, 见式(49)和式(50). 在公式中, 随着积分时间的延长, 柯西格林张量方程中的参数ϵi(i=1,2,3) 将 由无穷趋于 1,-1 和 1 . 这恰好与长轴比中间轴无限大、中间轴比短轴无限大的三轴不等椭球颗粒的取向方程一致, 即Λ1=1,Λ2=-1,Λ3=1 . 此时, 式(49)与式(50)完全一致. 随后Cui Z 和Zhao (2021)利用该特性结合三轴不等椭球颗粒求解过程提出了一种新颖的左柯西格林张量的方法, 详细内容可参见(Cui Z & Zhao 2021).

左柯西格林张量三个特征向量〈e1,e2,e3〉的时间演化方程

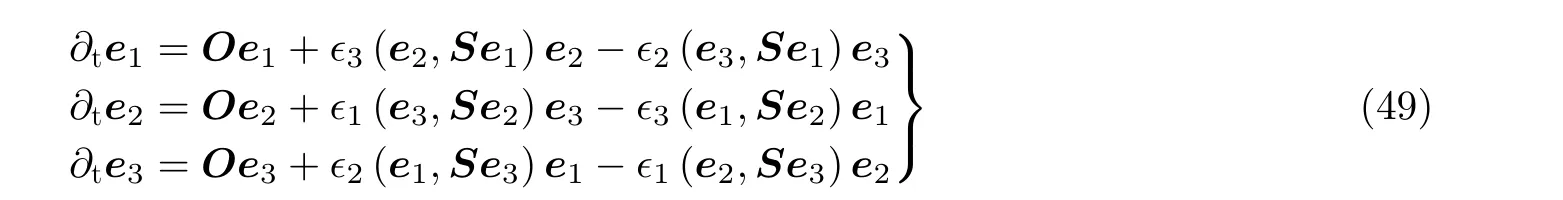
对应的三轴不等椭球颗粒的主轴〈p1,p2,p3〉的时间演化方程

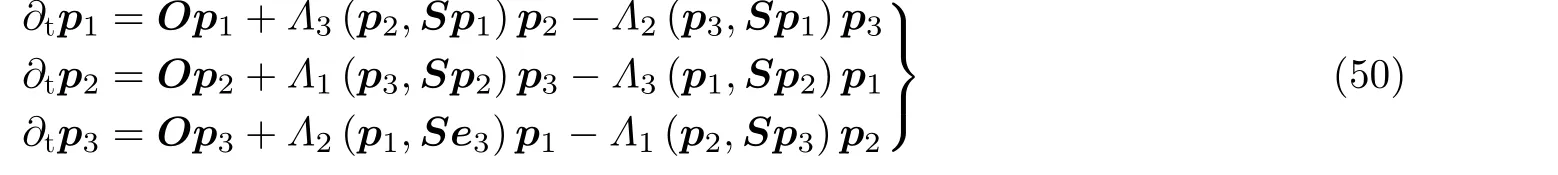
8 颗粒在湍流中的减阻控制作用

湍流的减阻控制在工业生产和交通输运等工程领域具有重要意义. 大量实验发现, 湍流里放入少量的添加剂, 如柔性聚合物、表面活化剂、气泡等, 可能产生一定的减阻效应. 其中柔性聚合物减阻明显, 且使用较为方便, 在许多领域得到了广泛应用. 但其不受强剪切, 不适用于剪切较强的流动中(Reddy & Singh 1985). 部分研究者通过实验发现刚性纤维可经受强剪切, 且同样具有减阻作用(Radin et al. 1975, Gyr & Bewersdorff 1995). 在数值模拟和理论分析中, 细小的刚性纤维通常被近似为无惯性的细长椭球颗粒 (如Brenner 1974, Gillissen et al. 2008) . 无惯性椭球颗粒通过额外的应力影响附近流体, 而反馈力和力矩则可忽略(Guazzelli & Morris 2011). Den Toonder 等(1997)首先利用直接数值模拟方法研究含细长颗粒的圆管湍流, 尽管他们简单地假定颗粒的取向沿着当地的流体速度向量的方向, 但仍然发现细长的刚性颗粒具有湍流减阻效应,且湍流统计结果与柔性聚合物的实验结果在定性上基本一致. Paschkewitz 等(2004)通过欧拉-欧拉双向耦合方法研究了最小尺寸槽道湍流中细长颗粒的减阻作用, 探讨了细长颗粒的布朗运动、体积浓度、长宽比和颗粒取向的封闭模型对减阻强弱的影响, 实现最大减阻率可达26%, 还提出了一种可能的湍流减阻机理. 他们认为细长颗粒在准流向涡之间的拉伸区会产生强烈的应力脉动, 从而减弱了近壁涡旋结构和改变了近壁湍流的自维持过程, 最终导致了湍流减阻现象,如图20 所示. Gillissen 等(2008)进一步发现细长颗粒在不同流动雷诺数下都具有湍流减阻效应.在这些数值模拟中, 颗粒相是在欧拉观点下结合封闭模型进行求解, 而非使用拉格朗日点颗粒法直接求解单个颗粒的动力学方程. Moosaie 和Manhart (2013)首次通过欧拉-拉格朗日双向耦合方法数值模拟了无惯性细长椭球颗粒与槽道湍流的相互作用, 同样发现了壁湍流减阻的现象和流动特征. 不过, 相比于细长颗粒, 扁平颗粒对壁湍流的影响的相关研究则非常少. 单向耦合的数值模拟结果表明, 长宽比较小的扁平颗粒也会产生强烈的颗粒应力脉动, 这意味着一定浓度的扁平颗粒或许能够调制湍流(Wang & Zhao 2020). Wang 等(2021)最近利用双向耦合的直接数值模拟, 研究了体积分数为0.75%的无惯性扁平颗粒和细长颗粒对槽道湍流的影响, 发现长宽比为100 的细长颗粒减阻14.93%, 长宽比为0.01 和0.002 的扁平颗粒分别减阻1.92%和7.15%. 他们提出了无惯性轴对称椭球颗粒的湍流减阻机理, 认为颗粒通过在展向和壁面法向对流体做的功抑制了准流向涡结构, 从而减弱了上抛下扫事件的强度, 导致了雷诺切应力的减小, 同时颗粒切应力会部分补偿雷诺切应力的减小, 两者之和的加权积分确定了阻力系数的大小. 对于扁平颗粒而言, 虽然雷诺切应力出现了明显减小, 但近壁区处较大的颗粒切应力减弱了湍流减阻的效果.

另一方面, 一些学者利用全分辨方法数值模拟含有有限尺寸颗粒的壁湍流, 发现有限尺寸的椭球颗粒也可能减小流动阻力. Ardekani 等(2017b)发现中性悬浮的扁平颗粒在近壁区转动较慢且回转轴倾向沿壁面法向, 这导致了流体雷诺应力和湍流产生项的减小, 从而产生湍流减阻.Eshghinejadfard 等(2018)观察到体积分数为10%的有限尺寸的扁平颗粒使得流体平均速度增加了1.3%. 他们提出, 展向速度脉动的减小和条带结构的展向间距增大是扁平颗粒减阻的主要原因, 而颗粒对涡结构的增强作用则抑制了减阻效果. Zhu 等(2018)数值模拟了含有限尺寸的细长和扁平颗粒的槽道湍流, 发现颗粒偏离球形的程度越大减阻越明显, 他们认为近壁区较低的颗粒体积分数和较小的流体雷诺应力导致了湍流减阻.

9 总结与展望

本文主要综述了非球形颗粒两相流的数值模拟方法、非球形颗粒在不同类型的简单流场与复杂湍流场中的运动行为的研究进展, 并对非球形颗粒取向与转动行为背后的机理进行了阐述与讨论. 根据目前的研究现状, 未来非球形颗粒两相流可能的研究方向包括:

图20纤维减阻机制示意图(Paschkewitz et al. 2004)

(1) 非球形颗粒在流体中受力模型的建立与完善. 在目前主流的非球形颗粒两相流的点颗粒模型中, 颗粒的阻力模型、力矩模型以及颗粒对流体反馈作用模型主要来自20 世纪Jeffery,Batchelor, Brenner 以及他们合作者的相关系列工作. 近年Dabade 等(2015)的流体惯性力矩模型是对非球形颗粒理论模型的重要补充, 但该模型的正确性与普适性还有待数值模拟以及实验的验证. 不过与球形颗粒相比, 非球形颗粒的模型依然还不够完善, 比如Maxey-Riley 模型中提及的压力梯度力、附加质量力以及Basset 历史力等模型在非球形颗粒问题中往往被人为地忽略. 对于非球形颗粒而言, 这些力的准确表达式以及其对非球形颗粒运动的具体影响尚不明确.目前, 除了从理论层面推导, 未来可主要通过全分辨数值模拟的手段研究单颗粒在简单流场中的运动来验证与分析相关模型的正确性, 或进行相关模型的建立与改进工作. 非球形颗粒模型的建立与完善, 一方面能帮助研究者对非球形颗粒行为进行精准捕捉, 进而改进目前的颗粒模拟方法, 从而进行大规模的非球形颗粒两相流的数值模拟, 另一方面能帮助研究者解释非球形颗粒复杂行为背后的机理, 为相关工业设计提供理论依据.

(2) 中高雷诺数非球形颗粒湍流两相流的研究. 目前绝大部分非球形颗粒两相流的数值模拟主要集中在较低雷诺数的情况, 有关非球形颗粒在中高等雷诺数的情况的研究屈指可数, 以非球形颗粒槽道湍流为例, 目前, 摩擦雷诺数Reτ超过1000 的直接数值模拟的工作仅Jie 等(2019)与Ouchene 等(2018)两项. 然而在实际的科学和工业问题中, 流场往往具有较高的雷诺数, 在高雷诺数下, 流动中会存在明显的大尺度结构. 大尺度结构对非球形颗粒的作用依然有待进一步研究. 与此同时, 对于高雷诺数的流场研究已经有比较成熟的大涡模拟的方法取代直接数值模拟.但大涡模拟是对小尺度的流动进行模化, 而非球形颗粒的运动行为又往往对小尺度的流动结构比较敏感, Chen 等(2016)的工作展示了不同流体的亚格子模式就会对非球形颗粒的转动与取向行为产生显著影响. 因此, 未来对非球形颗粒相关的亚格子模型以及对现有的湍流亚格子模型的改进依然是一个比较重要且十分具有挑战性的难题. 而最近的Pujara 等(2021)的工作表明无惯性椭球颗粒的运动行为具有形状与尺度的无关性, 这可能展示了湍流的某种拉格朗日不变量随湍流尺度无关. 这或许可以为非球形颗粒大涡模拟的研究工作提供新的研究思路.

(3) 非球形颗粒运动行为的机理分析. 非球形颗粒在流动中的复杂运动行为一方面由颗粒自身复杂的外形、颗粒惯性、颗粒运动学模型引起, 另一方面也受到颗粒周围的复杂的流动环境的影响. 目前有关非球形颗粒的机理研究存在两种基本方式, 第一种就是用当地的流场信息与颗粒运动行为建立对应关系, 比如涡量与变形率张量与颗粒行为的联系. 该方法的最大优点是直观, 但不可避免地忽略了颗粒拉格朗日运动的影响. 因此, 该类方法的最大缺点在于缺少拉格朗日信息, 且利用涡量与变形率解释颗粒取向并不具备普适性. 尽管该类方法在各向同性湍流中取得非常大的成功, 但是我们还是能看到其在具有强剪切的壁面以及准二维的流动中是基本上失效的. 而第二种方式就是利用拉格朗日拉伸与压缩方向来解释颗粒的取向行为, 这是从拉格朗日的观点出发进行解释, 且该方法包括了必要的拉格朗日信息, 因此椭球颗粒的取向与流体拉格朗日拉伸或压缩方向表现出极强的相关性. 然而, 该方法通常计算复杂, 需要得到大量的流体拉格朗日轨迹线, 且一般仅对于完全跟随流体质点的非球形颗粒有比较好的效果. 非球形颗粒运动行为的机理研究的主要目的之一就是能够希望通过周围的流场信息推测出非球形颗粒的可能运动行为, 从而可以实现颗粒行为的控制或者预测. 然而, 在实际问题中流场的情况非常复杂, 使用第二种方式分析和预测颗粒的取向行为需要花费较大的计算成本. 因此, 第一种方式将是比较经济且有效的. 那么如何在第一种方式的基础上或者其他方式, 提出更加有效的分析方法将可能是未来非球形颗粒两相流研究一个重要的方向.

(4) 复杂流场中复杂颗粒的运动行为. 本综述主要介绍了非球形颗粒在不可压牛顿流体中的运动行为, 且流动的几何边界非常简单. 未来可以从两个方面来拓展非球形颗粒两相流的研究范围. 一个方面, 可以通过改变流场属性、几何等特征, 比如非牛顿流、密度分层流、热对流或者可压缩流动, 或研究粗糙壁面湍流、射流等复杂流动问题中的颗粒行为. 另一方面, 可以通过改变颗粒模型进而研究不同非球形颗粒模型对颗粒运动行为的影响, 比如游动、颗粒形状反对称、质心偏置等. 另外, 有关结合机器学习的智能颗粒的研究在近些年也得到了广泛地关注, 相关综述可见(邱敬然和赵立豪 2021).

致谢

国家自然科学基金(11 702 158, 11 911 530 141)和清华大学国强研究院(2019GQG1012)资助项目.