力学超材料研究进展与减振降噪应用

尹剑飞 蔡 力 方 鑫 肖 勇 杨海滨 张弘佳钟 杰 赵宏刚 郁殿龙 温激鸿

国防科技大学装备综合保障技术重点实验室, 长沙 410073国防科技大学智能科学学院, 长沙 410073

1 引 言

突破材料/结构力学性能的极限是工程领域永恒的追求. 力学超材料概念的产生和发展为实现这一目标提供了新的视角和源动力. 力学超材料是以介观尺度的人工微结构为基本单元构造的复合材料或结构, 具有天然材料所不具备的超常静力学或动力学特性. 这些超常特性通常不依赖于自然材料组分和本构关系, 而是取决于微结构单元本身及其与周围单元和介质之间的相互作用, 这就为力学性能的调控和设计提供了丰富、灵活的自由度, 因而获得工程领域的广泛关注. 近年来, 力学超材料的相关基础理论、特性机理、设计方法等研究迅速发展, 在航空航天、车辆船舶、工程建筑、军事国防等领域逐渐展现出广阔的应用前景(温激鸿等 2018, 于相龙和周济 2019).

力学超材料通常是具有周期特性的人工复合材料/结构 (基本发展脉络如图1 所示) , 其相关工作可以追溯到对工程周期结构力学特性的研究. 20 世纪50 年代, 以加筋板、蜂窝材料、点阵材料、超轻多孔材料为代表的人工周期材料/结构, 因具有轻质、高刚度、高强度等优异静力学特性而在工程中得到广泛应用(Christensen 2012, Jones 2014). 由于这类材料/结构对动载荷更为敏感, 在外部声振作用下更容易激发弹性波传播(Mead 1971, Lee & Yang 1973), 而工程领域往往对弹性波传播引起的振动和噪声量级有着严格的要求, 因此, 工程周期材料/结构的动态响应特性和波调控问题得到重视. 以英国南安普顿大学声学与振动研究所 (Institute of Sound and Vibration Research) 为代表的研究机构和团队, 在周期结构动力学特性方面开展了大量的工作(Mead 1996). 其中, Gupta (1970, 1971, 1972)在研究周期梁、加筋板的振动时, 深入揭示了周期结构中的弹性波带隙特性, 建立了周期结构模态特性与其色散特性的联系, 发现了能带边界频率与周期单元 (元胞) 和有限周期结构模态频率之间的关系. 这些研究成果被用于指导周期结构的设计, 实现对弹性波传播及振动与噪声抑制的优化.

这种基于能带结构分析人工周期结构动力学特性的研究思路, 在引入凝聚态物理、电磁学、光学等领域研究进展的基础上, 得到极大的丰富和发展, 最典型的标志就是声子晶体、声学超材料概念的提出. 20 世纪90 年代初, 类比光子晶体, Sigalas 和Economou (1992)提出了声子晶体的概念, 即具有弹性波带隙的质量密度及弹性常数周期性分布的人工材料/结构. 通过将电子能带理论研究中发展起来的概念和分析方法系统地引入到周期性材料/结构的弹性波传播特性分析中, 更加深入地揭示了周期结构中弹性波传播和调控的机理. 声子晶体概念提出伊始, 重点关注带隙产生及调制机理(Kushwaha et al. 1993, Kushwaha & Halevi 1996, Kushwaha 1997)和实验验证(Sanchez-Perez et al. 1998, De Espinosa et al. 1998). 此外, 研究者还发现了声子晶体可以实现波的定向传播(Qiu & Liu 2006, Wen et al. 2009, Tang et al. 2015)、缺陷态和局域化(Sigalas 1997, 1998; Torres et al. 1999)、负折射(Zhang & Liu 2004, Hu et al. 2004)、声学共振隧穿(Qiu et al. 2005a)等多种新奇效应. 这些研究不但深化和丰富了弹性动力学基础理论, 而且在振动与噪声控制(Richards & Pines 2003, Romeo & Luongo 2003, Yu et al. 2008, Sánchez-Dehesa et al.2011)、声波定向发射与声波导设计(Ruzzene et al. 2003, Yang et al. 2004)以及高分辨率声成像(Ke et al. 2005, Qiu et al. 2005b)等方面具有潜在应用价值.

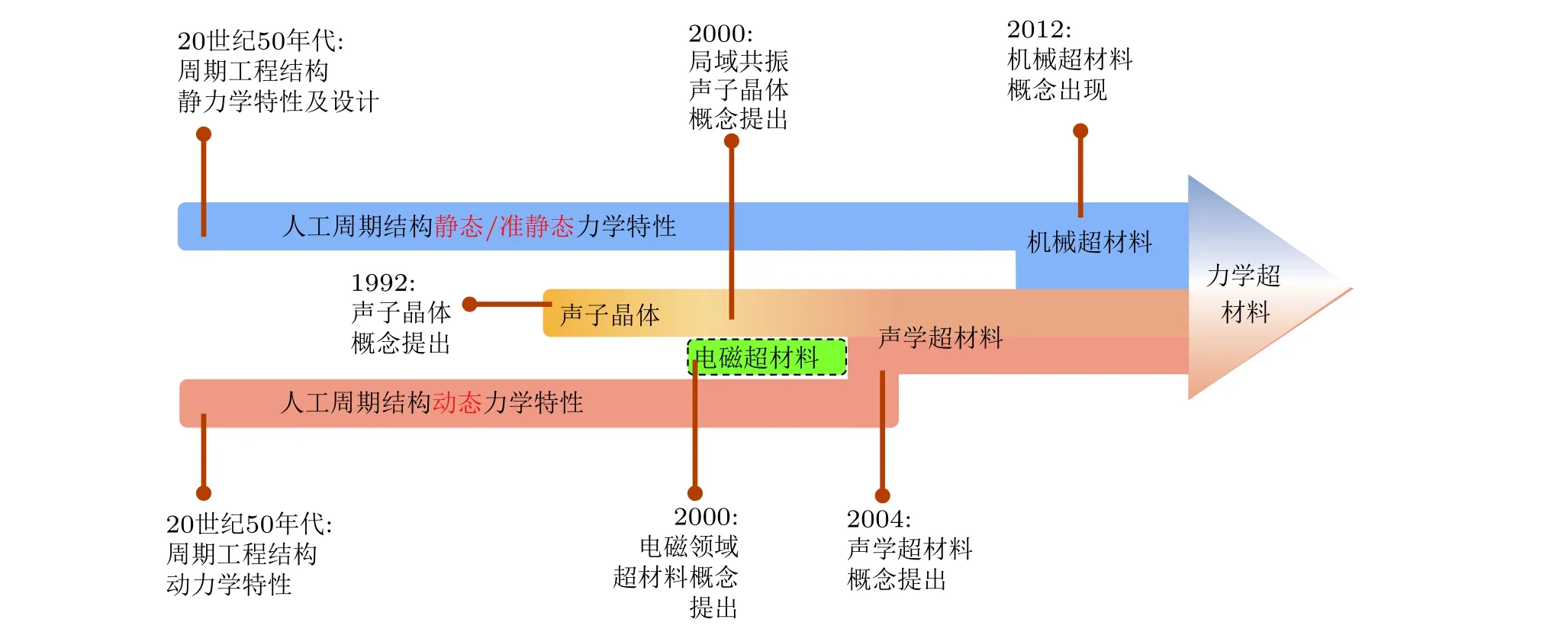
图1力学超材料发展历程简图

传统声子晶体带隙形成主要基于Bragg 散射机理, 带隙频率位置受Bragg 条件控制(Brillouin 1946), 即晶格尺寸至少要与弹性波的半波长大致相当. 因此, 要实现低频波控制, 需要较大的元胞尺寸, 这在一定程度上限制了声子晶体的工程应用. 直到2000 年, 香港科技大学 Liu 等(2000) 提出了基本构型如图2(a)所示的局域共振声子晶体: 通过在弹性介质中周期排列由软橡胶包覆硬铅球构成的局域共振单元, 发现了材料存在一个远低于Bragg 带隙频率的低频带隙(图2(b)) , 并将这一带隙的产生归结于共振单元的谐振效应, 就此将声子晶体波调控范围扩展至亚波长频段. 与此同时, 在电磁领域, 基于亚波长结构调控电磁波传播的研究也取得了突破性进展. 研究者通过引入亚波长尺度谐振结构, 实现了介电常数和磁导率同时为负的“左手材料”或“双负材料”, 并从实验上验证了材料具有的负折射特性(Shelby et al. 2001). 研究者将这类材料称为超材料, 其英文“metamaterial”中“meta-”源于希腊语, 有“超出、另类”之意, 突出了超材料异于自然材料的特性. 电磁超材料和局域共振声子晶体两方面的研究进展表明: 在声波/弹性波调控中, 基于亚波长尺度的结构单元设计, 有可能大范围调节材料的力学性能, 甚至得到超常的力学特性参数. 基于这一思想, 2004 年, 香港科技大学Li 和Chan (2004)研究了由软硅橡胶散射体埋入水中构成的固/液复合人工结构, 发现在亚波长频段的一定频率范围内, 等效质量密度和等效体积模量同时为负值, 即也表现出所谓的“双负”声学参数特性, 因此类比电磁超材料, 提出了声学超材料的概念 (acoustic metamaterial) . 声学超材料利用局域共振单元(Liu et al. 2000)、亥姆赫兹共振腔(Fang et al. 2006)、蜷曲空间单元(Liang & Li 2012)等特殊设计的具有谐振特性的基元, 能够实现在亚波长尺度上对弹性波/声波的调控, 突破了传统声子晶体Bragg 条件对元胞尺寸的约束, 在低频减隔振/隔声/吸声、亚波长声聚焦、声波/弹性波斗篷设计等方面提供了新的技术路径.

图2局域共振声子晶体及其低频带隙. (a)结构示意图, (b)声波传输特性及能带结构(Liu et al. 2000)

近年来, 随着3D 打印、激光选熔等先进制造技术的不断发展, 制备具有更加复杂微结构的力学超材料成为可能, 推动了其研究范畴从动态波动特性调控进一步扩展至静态弹性力学性能,如弹性模量、泊松比、刚度、强度等力学参数的调控. 同样基于微结构设计, 力学超材料可以实现负泊松比 (于靖军等 2018) 、五模反拉胀 (陈毅等 2016)、轻质超强 (Schaedler et al. 2011,Zheng et al. 2014)、负刚度 (Lakes et al. 2001a)等反常奇异机械力学特性, 很多文献也将这类人工材料/结构称为“机械超材料”(Lee et al. 2012, 于相龙和周济 2016). 事实上, 有些类型的机械超材料早在超材料概念提出前就已经开展了较为深入的研究, 如Lakes (1987)在20 世纪80 年代就发现并研究了人工负泊松比材料的特性. 但在力学超材料的体系框架内, 材料参数调控的范围更加系统完整, 已有研究也得到了进一步发展, 同时不断发现更多的奇异力学特性.

可以看到, 不管是声学超材料还是机械超材料, 其核心思路都是通过人工微结构单元构筑材料/结构, 实现超常力学行为, 因此可以将它们统称为力学超材料. 其灵活的可设计、可调控性为传统结构功能材料设计提供了全新的自由度和范式, 进而有可能通过微结构设计调节力学约束, 形成低频波动控制与静载兼顾的功能-结构-材料一体化设计理论. 本文将对力学超材料典型的超常力学特性和效应进行总结, 进而结合不同工程应用背景, 重点讨论其在水声/空气声调控、减振抗冲设计方面的应用研究进展. 最后, 对可编程及智能超材料、非厄米力学超材料、弹性/声学拓扑材料等领域前沿研究进行简述.

2 力学超材料的超常特性及新奇效应

具有微结构单元的力学超材料通常在宏观上被视为均匀介质进行分析, 因此其所具有的力学特性和效应可以通过等效的力学、物理参数来描述和表征. 这些等效参数源于微结构设计, 体现了不同尺度力学性能之间的耦合. 面向动态波调控和静态力学性能调控的力学超材料, 所关注的等效力学参数也各不相同.

图3力学超材料的动态力学参数调制空间

在声学/弹性波超材料研究领域, 动态等效参数主要通过质量密度ρ和弹性模量κ来描述. 以κ和ρ为x和y坐标轴建立二维坐标空间 (如图3 所示) , 自然界中的天然材料通常二者都为正值, 即材料参数只能位于该空间的第一象限. 这主要是由于均匀介质受外力作用时, 各质点产生与外力同方向的惯性加速度和弹性变形, 因此质量密度和弹性模量均为正值. 而力学超材料通过人为引入局部运动与变形模式, 使材料或结构中的受力分布和作用不再是均匀的, 微结构和基体间产生相对运动和相互作用, 增强了局部-整体运动之间的耦合, 此时材料整体受力应为外部激励力与内部相互作用的内力之和. 这时在分析宏观等效质量密度与弹性模量时, 内部的相互作用起明显作用, 在某些频段甚至起主导作用, 因此可以将等效参数的调节范围拓展到其他象限.

对于由软橡胶包裹高密度芯体构成结构基元的局域共振超材料, 研究发现其波能量传输系数具有显著的Fano 谐振特征, 意味着弹性波在其中传播时, 基体材料与亚波长基元间的相互耦合作用产生明显的局部能量增强效应(Rybin et al. 2009). 图4 基于声散射动力学模型得到了材料动态等效质量密度及共振单元位移随频率的变化关系. 从图4(a)可以发现, 在共振频率附近,等效质量密度会发生剧烈变化, 特别是在低频带隙对应的频段, 等效质量密度变为负值. 在动力学分析中, 质量密度是描述物质在外力作用下产生运动响应的特性的物理量. 负的质量密度意味着该频段内材料对外部弹性波的激励产生负的响应. 超材料中的每一个局域共振单元可视为由质量-弹簧组成的局域振子结构, 高密度芯体充当振子的质量, 软包覆层充当振子的弹簧. 由于材料整体响应函数～ 1/(ω02-ω2), 所以在振子共振频率ω0附近, 响应会突变为负, 即局域共振单元整体相对于基体介质中传播的弹性波而言做反相的运动, 如图4(b)所示. 当超材料中局域共振单元的填充率足够高时, 材料整体的响应特性受局域共振单元响应主导, 使得材料整体的运动与激励弹性波反相, 从而导致负动态质量密度.

图4局域共振超材料的等效质量密度(a)及芯体位移(b)随频率的变化规律

如果在力学超材料中同时引入单极共振和偶极共振单元, 并通过参数设计使二者负参数作用频段相近, 就可以构造具有双负特性的力学超材料. Ding 等(2007)基于这一思想将三维三组元偶极共振单元和空泡单极共振单元嵌入同一基体中, 构造了具有双负特性的力学超材料. 从图5 的能带结构可以看到, 双负材料在质量密度和弹性模量分别为负的带隙频段出现了一条新的纵波能带, 说明等效质量密度和弹性模量同时为负时, 波能够在介质中传播. 这一特性也通过实验得到了验证(Lee et al. 2010).

类比介电常数与磁导率均为负的电磁超材料, 声波在双负介质中传播时同样具有负折射率特性. 如将双负介质制成具有足够厚度的平板结构, 声波入射时可以产生亚波长声聚焦效应(Luo et al. 2003, Guenneau et al. 2007, Ambati et al. 2007, Zhu et al. 2011, Christensen & de Abajo 2012), 即入射波通过负折射产生两次汇聚, 并在平板的另一侧实现类似凸透镜的聚焦成像效果(Pendry 2000). 传统正折射率透镜声成像存在与频率相关的分辨率极限(Fang et al.2005), 不能实现对亚波长尺度结构的精确成像, 而力学超材料基于倏逝波与声表面波模式耦合的成像机理可以克服分辨率极限, 理论上分辨率可以无限提高, 在声成像与无损检测等声学器件设计方面具有潜在应用价值.

图5单负及双负力学超材料能带特性. (a) 偶极局域共振单元能带结构 (软包覆层+硬质芯体单元),(b) 单极局域共振单元能带结构 (水基空气泡单元), (c) 混合局域共振超材料能带结构(Ding et al. 2007)

除了在声波调控方面, 力学超材料的负质量密度、负模量及“双负”特性也在固体和结构弹性波系统中得到了验证. 如北京理工大学胡更开团队通过实验验证了固体结构超材料的负质量特性(Yao et al. 2008), 还设计了具有 “双负”特性的弹性力学超材料, 验证了力学超材料中的亚波长弹性波负折射特性(Liu et al. 2011a, Zhu et al. 2014).

以上研究工作主要是针对体材料动态力学参数的调控, 在此基础上, 近年来亚波长结构对表面波的控制也成为力学超材料关注的热点之一. Garcia-Vidal 等(1998)在银膜亚微米孔阵列结构中得到了由表面特性引起的、与传统透射理论不符的亚波长频段光波异常透射增强现象, 随后又陆续实现了基于超材料表面的遂穿、超透镜及慢波等控制效果. 研究者将这一类基于亚波长表面模式的波调控效应称为超材料的表面反常效应. Christensen 等(2008)研究了声波在含亚波长狭缝表面的传播特性, 发现了波长远大于狭缝宽度的反常透射现象, 说明力学超材料同样可以产生亚波长反常增透等表面反常效应. 电磁超材料的表面反常效应通常认为与表面等离激元(SPP)等表面倏逝波模式相关. 在力学超材料中不存在直接与SPP 对应的表面波模式, 但弹性波在流固耦合界面也存在Stoneley 波等特有的表面波模式(Zhou et al. 2010, Christensen et al.2010), 也可以在亚波长频段实现对弹性波的有效调控. 表面波模式在沿表面方向能够产生较大的传播波矢量和较慢的传播速度, 有利于用更小的结构尺寸实现对波的控制.

传统力学超材料的研究主要关注其动态波控特性, 近年来, 面向静态力学特性的设计与调控成为力学超材料领域新的研究生长点. 对弹性固体来说, 剪切变形与压缩变形间往往是相互联系、相互制约的, 如各向同性介质的体积模量K、剪切模量G和泊松比ν之间一般满足K/G=[2(ν+ 1)]/[3(1-2ν)]. 自然界中一般常见的固体材料体积模量和剪切模量均为正, 且泊松比主要在0.25 ～ 0.35 间变化(Greaves et al. 2011), 即处于图6(a)所示Milton 图的第一象限中的局部区域, 意味着材料的体积模量和剪切模量数量级相同(Milton 2004). 通过微结构设计, 引入易变形、局部松散模式, 力学超材料可以对弹性变形间的约束进行有效调节, 解除或减弱材料各参量之间的耦合关系, 进而扩展静态力学性能的可设计范围, 实现反常特性, 如泊松比为-1 (G轴) 或泊松比为0.5 (K轴) 的极端情况, 还可以实现泊松比、压缩性、刚度为负的特性. 另外, 如图6(b)所示, 在描述材料杨氏模量和密度之间的耦合关系的Ashby 图中(Gibson & Ashby 1999), 一般材料的杨氏模量增大会导致材料密度的增大, 而力学超材料也可以打破这一规律, 实现高刚、高强等优异力学特性.

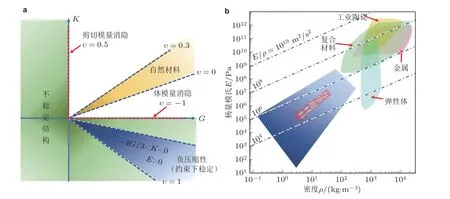
图6力学超材料静力学参数调制空间. (a) 基于Milton 图的力学超材料参数调制空间, (b) 基于Ashby 图的力学超材料参数调制空间 (Zheng et al. 2014)

通过结构单元设计, 力学超材料可以实现剪切模量是体积模量的高阶无穷小量(陈毅等2016) , 此时材料参数位于Milton 图正K轴上, 即泊松比为0.5. 由于整体等效弹性特性在应力空间中, 只有体积压缩模式的特征值不为零 (对应的特征向量称为硬模式) , 而对应剪切的特征值为零 (对应的特征向量称为软模式) , 这是一般固体介质所不具备的性质, 又被Milton 和Cherkaev (1995)称为五模材料 (pentamode material) . 五模材料具有类流体的力学属性, 仅支持单模式的弹性压缩纵波, 在静态力学性能调控和动态波控方面均有较大应用前景. Kadic 等(2014)发现五模超材料具有与一般材料不同的质量密度和刚度解耦特性, 基于五模单元理论上可以设计具有任意正定弹性张量的晶格结构, 实现介质中应力空间分布的调控. 研究者根据这一特性设计了使目标对作用力隐蔽的“无感斗篷”(Bückmann et al. 2014). 在动态波调控方面, 如图7(a)所示, 二维五模材料中的弹性波能带结构表明其在亚波长频段的相当带宽内, 只有线性的纵波色散曲线存在, 说明该材料的特性与流体类似. 通过调节结构参数使等效质量密度和体积模量与水匹配, 可以实现水中声波入射至五模固体基材料时不产生明显的扰动 (如图7(b)所示) ,因此这类力学超材料又被称为“金属水”(Pendry & Li 2008, Norris 2009). 在此基础上, Zheng 等(2019, 2020a) 通过在五模超材料中引入负泊松比微结构设计, 可以在指定方向上实现仅对剪切波的支持, 从而形成一种“反流体”的波动特性, 从而实现弹性波的宽频极化控制. Martin 等(2012)还将二维五模材料扩展至三维, 研究了三维五模微结构的能带特性, 同样发现了其在较宽频带内具有类水特性.

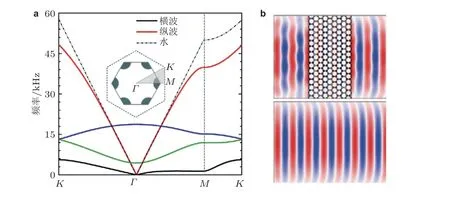
图7(a) 五模力学超材料能带结构, (b) “金属水”五模力学超材料的类水特性 (陈毅等 2016)

除了使弹性特性接近Milton 图的K轴, 力学超材料也能向G轴方向调节其弹性特性, 使得泊松比变小, 甚至变为负值. 这时超材料表现出反常于一般弹性材料的拉胀特性, 如横向受拉时,材料会在纵向上发生膨胀, 反之受压时材料向内部聚集, 瞬时密度增大, 因此能够表现出刚度和韧性增强的特性. 当泊松比恰为-1 时, 意味着材料的体积模量K远小于剪切模量G, 此时, 材料仅支持易变形模式, 即在外力作用下, 其形状不会发生变化, 而是随着外力的变化发生整体尺寸的缩放, 这种材料又被称为胀缩材料(Milton 2015). 负泊松比材料的拉胀特性使其具有抗冲击、抗断裂、吸能隔振、曲面同向性等优异力学性能, 已经在各类结构功能材料中得到应用.

自然材料绝大多数位于Milton 图中第一象限上, 意味着其体积模量和剪切模量均为正, 从而保证弹性张量为正定, 即材料系统的稳定性. 力学超材料的弹性特性参数也可以扩展到Milton 图其他象限中, 实现负弹性模量的力学超材料, 使材料在宏观上展现出负压缩性或负刚度特性. 当材料参数处于Milton 图的第四象限中, 满足杨氏模量E＞ 0 和-4G/3 ＜K＜ 0 时, 材料在受到压力作用时, 在某一个方向或是几个方向上进行膨胀, 产生负压缩模量特性; 另一种具有负模量特性的力学超材料是负刚度超材料. 相比于一般材料在受力方向上产生形变而形成反作用力, 具有负刚度的材料变形与受力方向相反, 形成与受力方向相同的辅助力. 在无约束条件下,负模量力学超材料通常是不稳定的, 这种特殊的力学效应只有在受力系统从一个稳定状态向另一个稳定状态转变时产生(Lakes & Wojciechowski 2008). 在实际应用中, 往往通过在负模量材料中施加额外约束, 使其具有一定的稳定性. 负刚度和负压缩材料具有许多优异的力学特性, 比如可以实现结构同时具有高刚度和高阻尼特性, 因此在减振抗冲材料与器件设计方面展现出良好的应用前景.

本节简要归纳了力学超材料在动态波操控和静态力学性能调控方面的主要特性. 下面将以典型工程应用为主线, 重点论述基于力学超材料思想的装备减振降噪及隐身防护方面的研究进展、挑战和发展趋势.

3 基于力学超材料的水声调控

随着我国海洋强国战略的持续推进, 水声探测、声隐身、水声通讯等领域对水下声波调控技术提出了更高的要求. 声学覆盖层是敷设或安装在水下装备上用于吸收、隔离和调控水声声波的功能材料, 是对抗主被动声呐探测、提高自身水声通讯和声呐探测性能的关键技术手段. 如图8 所示, 按照声学功能的不同, 声学覆盖层主要包括: (1) 水声吸声材料, 主要用于吸收主动声呐探测声波、本体自噪声等; (2) 水声隔声去耦材料, 通过构造阻抗失配, 隔离和阻断内部结构振动向水中辐射噪声或声透射; (3) 水声绕射调控材料, 主要用于调控声呐探测声波入射至材料后的传播方向, 改变回波特性, 实现“无声影”隐身.

当前, 随着声呐探测频段不断向低频拓展, 具有低频、宽带、薄层、耐压特性的水声材料成为水声调控技术发展的重要目标. 对于吸收和去耦型水声材料, 材料内部的变形能力是决定材料水声调控性能的主要因素. 为满足材料的静态力学设计要求 (如耐静水压) , 一般需要约束材料和结构内部变形与运动, 但随着这种约束程度的增强, 在动载荷下材料和结构对波动能量输运的调节能力也随之减弱. 这样往往导致材料对低频波动的耦合作用弱、难以实现高效吸收或隔离.由于缺乏新设计原理指导, 低频水声材料的设计与研制进展缓慢, 已成为水下装备声隐身急需解决的瓶颈问题.

力学超材料通过微结构调节内部变形与运动约束, 形成软变形谐振甚至产生局部机构位移模式, 可有效增强材料与波相互作用, 进而提高对波动能量输运调控能力, 有望解决传统水声材料变形约束与波动耦合间的矛盾, 克服小尺寸结构低频波耦合作用弱、调控能力差等难题. 此外, 基于变换声学理论, 力学超材料也为实现声波绕射隐身提供了实现途径, 以五模力学超材料为代表的水声绕射隐身技术成为近年来研究的新热点.

3.1 水声吸声材料设计

传统水声吸声材料主要基于阻抗匹配和阻尼耗散这两个基本原理进行设计(王育人等2017). 通过引入分层、尖劈等阻抗渐变型结构, 使材料特性阻抗尽量与水匹配, 从而减少界面反射声波, 使声波最大限度的进入吸声材料; 同时, 基于橡胶类黏弹材料的高阻尼特性, 实现材料内声能量的耗散. 由于均匀材料中压缩变形的损耗因子很小, 为了促进声波阻尼耗散, 主要采取两种方法: 一是在材料中引入气泡、微粒等散射体, 使入射波发生多次散射, 延长波传播路径,增强能量耗散; 二是在材料中嵌入周期排列的空腔结构, 通过空腔谐振作用将材料中的纵波转化为损耗因子更高的剪切波, 提高能量耗散效率. 空腔零阶共振耗散是传统材料的核心低频吸声机理, 但由于谐振频率主要取决于空腔尺寸及基体材料的模量, 降低吸声频率意味着增大空腔尺寸或减小基体材料的弹性模量, 因此, 在水下压力工作环境及材料厚度约束条件下, 声学空腔结构难以实现低频 (2 kHz 以下) 水声的有效吸收, 是当前水声吸声材料设计的主要挑战.

图8声学覆盖层水声调控功能示意图. (a) 吸声材料, (b) 隔声/去耦材料, (c) 声绕 射材料

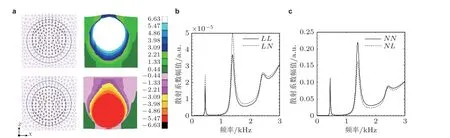
图9(a)局域共振单元在共振频率附近的运动位移图(上组图表示正向运动, 下组图表示逆向运动);水声超材料中局域共振单元的各阶散射系数: (b) 纵波入射; (c) 横波入射

2006 年, 国防科技大学温激鸿团队发现局域共振力学超材料所具有的低频强吸声效应可以用于水声吸声材料设计中, 并验证了经过水声应用适应性设计后的力学超材料在共振频率附近具有超常低频水声吸声特性(Zhao et al. 2007). 图9(a)中有限元模型的数值仿真结果表明, 强吸声频率附近, 局域共振单元的位移主要集中在芯体内部, 整个芯体的振动基本上是等幅的, 展现出刚体共振的模态. 芯体的运动推动包覆层产生相应的振动, 其标志为位移幅值从内部到包覆层外表面逐步减小, 因此芯体和包覆层可以视为一个质量-弹簧系统. 进一步通过采用多重散射法分析共振频率处吸声增强的机理(赵宏刚 2008). 如图9(b)和(c)所示, 相比纵波入射条件下, 纵波向横波的散射系数LN要高于纵波向纵波的散射系数LL; 对于横波入射, 横波向横波的散射系数NN要高于横波向纵波的散射系数NL. 这意味着在水声环境中, 入射纵波经过局域共振单元散射后, 芯体的平移振动和包覆层的剪切变形使得入射纵波高效的向横波转换, 声散射过程中也仅有少部分横波转化回纵波. 由于横波在黏弹橡胶中具有较高的损耗因子, 因此显著增强了对声波能量的耗散.

图10水声吸声力学超材料的微结构单元设计

图9 中的球形局域共振单元存在密度较大, 吸声频段较窄等问题, 在工程应用方面具有局限性. 吕林梅等 (2012)进一步设计了如图10(a)所示的柱形局域共振结构, 相同体积时圆柱芯体高度可小于球体直径, 提高了基体厚度方向的利用率, 可以有效降低材料整体厚度. Meng 等(2012)及Ivansson (2012)采用遗传算法、差分进化算法等数学优化方法开展了水声吸声超材料的吸声优化设计研究, 提出通过多尺寸局域共振结构的耦合设计实现吸声频带的有效扩宽.Zhong 等(2015)研究了芯体偏心对局域共振覆盖层吸声性能的影响, 发现利用局域共振单元芯体偏心可调节芯体共振模式的频率位置, 通过将芯体共振模式与钢板背衬引起的覆盖层整体共振模式的耦合也可显著拓宽低频吸声带宽. Shi 等(2019)设计了内含多层局域共振结构的复合共振单元, 通过仿真方法研究了多层复合型局域共振超材料的共振模式及吸声特性, 发现单元内多个局域共振模态耦合可扩宽带隙或产生多个带隙. Gu 等(2021)设计了元胞内含有多个共振单元的局域共振超材料 (图10(b)) , 在共振耦合和单元多重散射作用下, 可以实现200 ～ 2000 Hz 的低频吸声特性, 且由于局域共振单元为实心结构, 材料与空腔结构相比具有更优异的耐压性能.

另一种拓宽吸声频带的设计思路是将传统空腔型吸声结构与局域共振结构集成设计(Jin et al. 2020, Gao & Lu 2020). 如图10(c)和(d)所示, 这一思想可以充分发挥空腔高频吸声和局域共振低频吸声优势, 实现低频宽带的高效吸声. Yang 等(2019a)从散射体共振散射与吸收特性的角度比较分析了局域共振力学超材料与传统声学空腔结构的吸声机理, 并验证了局域共振结构与声学空腔形成的耦合宽频吸声效应.

除了局域共振与空腔结构，研究者还探索了更多的力学超材料微结构单元的设计方案. Jiang等(2009)和Chen 等(2016a)将梯度木堆结构引入局域共振声超材料中, 使之具有复式晶格, 即一个原胞内含有两种正交的共振子, 如图10(e)所示, 通过共振子单元之间的强耦合作用可以进一步展宽带隙实现声波的宽频强吸收. Jiang 和Wang (2012)利用泡沫铝骨架包裹不同性质的聚氨酯高分子材料, 并通过互穿网络结构设计, 构建了具有宽频强吸声和耐压双重特性的声子玻璃(图10(f)) , 在5 kHz 以上频段上取得了较好的宽频吸声效果. Zhang 等(2018a)提出了用于低频水声吸收的一种薄板型超构材料, 发现其在橡胶类基材中的弯曲共振吸声效应. Duan 等 (2021)受空气声超材料研究的启发, 提出了一种基于Helmholtz 共振与橡胶材料形变耗散的水声超材料, 发现其在理想刚性边界条件下具有显著的低频强吸声效应. Zhong 等(2019a)提出了一种含螺旋式振子结构的水声超材料, 通过理论和实验研究验证了其低频高效吸声特性. Zhao 等(2014)分析了钢背衬声散射对局域共振结构的低频吸声的影响, 结果表明钢背衬和局域共振声耦合, 可增强其亚波长低频吸声性能. 研究进一步揭示了钢背衬条件下复合局域共振结构与钢背衬间的整体共振 (驻波) 吸声机制, 钢背衬板可视为引入一个低频弹簧质量模态, 对应频率可低于局域共振频率, 该模态频率处吸声达到峰值, 钢板越厚, 该吸声峰越往低频移动. Zhong 等(2019b) 利用钢板背衬引起的整体共振吸声模式, 进一步推导得到了声学覆盖层实现低频宽带完美吸声的理论要求, 并反向设计得到了能够在3 cm 厚度下实现500 Hz 频率处准完美声吸收的声学超表面结构.

此外, 基于非共振超材料的吸声设计最近也获得关注. Yuan 等(2018)提出一种基于石墨烯微片-橡胶复合的水声吸声材料, 水声管测试结果表明, 该结构可通过石墨烯微片的高比表面积导致的阻尼损耗增加及其高热传导率实现对2 ～ 30 kHz 水声吸收的增强, 并兼具良好的力学性能. Gao 和Zhang (2018)提出黏弹性层内嵌螺旋金属环的水声超材料, 有限元结果表明, 22 cm厚的该结构可使中低频纵波向剪切波发生有效波形转换, 并通过基体黏弹性损耗, 实现1 kHz 以下低频宽带吸声.

3.2 水声去耦材料设计

水声去耦材料主要用于隔离艇体结构振动能量向外界传递, 还兼具隔声、阻尼功能, 从而降低艇体辐射噪声, 它是与吸声材料相辅相成的降噪技术. 去耦材料通常在黏弹性基体中加入空腔等散射体以减小材料等效纵波声速, 形成阻抗失配; 同时通过空腔谐振的波形转化效应, 增大声能向热能转化效率, 实现对能量的阻隔和耗散. 对于去耦材料声学性能的研究, 主要从微观和宏观两个尺度上进行. 微观主要从材料属性和声学结构来入手, 建立去耦材料元胞级声传递 (隔声) 模型, 获得材料本征声学性能. 为了分析在振动激励下去耦材料声学性能, Huang 等 (2015)建立了基于元胞模型分析无限大板结构在线力激励下的声辐射特性 (图11(a)所示) , 并发现其振动声辐射特性与隔声特性 (图11(b)) 具有相似的规律. 因此, 目前对于微观尺度去耦性能的研究大多选用两端均为水介质的隔声模型. 在宏观尺度上, 主要研究敷设去耦超材料的有限大板、壳类结构在水下的振动和声辐射特性, 通常采用数值仿真和实验的手段开展(姚熊亮等 2009, 钱德进等 2011).

目前, 工程中去耦材料主要采取内嵌空腔的结构形式. 研究发现, 空腔体积越大, 其阻抗失配作用越强, 总体去耦性能越好 (张燕妮等 2020); 但空腔型去耦材料在艇体结构与水域之间形成类似弹簧的作用, 从而引入艇体结构低频共振效应, 当去耦材料的隔振性能无法抵消艇体共振产生的振动增强时, 可能导致低频去耦失效(黄凌志等 2015). 而且, 从工程应用的角度, 大尺度空腔结构使材料耐压性能下降, 容易发生破坏. 因此, 在保证耐压等力学性能的前提下, 提高去耦材料的低频隔声性能是当前研究的重点. 为解决这一问题, 研究者提出将局域共振型力学超材料引入去耦材料设计, 发现其在吸收外部入射声波的同时, 还对内部辐射声波具有隔离的效果,尤其在局域共振频率附近, 材料具有优异的低频隔声效果(Huang et al. 2016), 这源于局域共振结构的低频复等效密度特性对结构阻抗的影响作用. 但是, 采用单一局域共振单元设计隔声去耦材料, 同样存在隔声频带往往较窄的问题, 难以满足水声宽带隐身的需求.

图11水声去耦材料声学性能分析模型

通过对球形多层局域共振力学超材料的弹性波能带进行分析, 发现材料存在布拉格散射与局域共振两种带隙特性. 图12(a)描述了局域共振带隙和布拉格带隙频段随共振单元材料参数的变化规律, 表明随着包覆层横波声速的增加, 局域共振隔声频带逐渐向布拉格隔声带靠拢, 而布拉格隔声带的低频边界保持不动(Yuan et al. 2013). 这说明共振单元的引入能够明显降低超材料的宏观等效声速, 使得位于高频段的布拉格散射带隙的频带降低. 在此过程中, 局域共振隔声频带的带宽得以拓宽, 而布拉格隔声频带的衰减程度也得到了增强. 当横波声速增大为一特定值 (cCS= 114 m/s) 时, 单元的共振频率恰好与布拉格散射的低频边界重合, 这时两种隔声带耦合在一起, 展现出宽频隔声特性. 如果横波声速继续增加, 耦合带隙会重新相互分开, 并且两者的位置发生了对调, 而两种隔声频带的带宽都在逐渐缩减.

基于这一认识, 通过材料及结构参数设计, 可以实现在低频段局域共振和布拉格散射带隙的耦合, 从而拓宽水声隔声带宽. 图12(b)为带隙耦合时的局域共振超材料的能带结构. 可以看到,两种带隙的耦合效应使得超材料的纵波模态在归一化频率 [0.27, 0.84]处展现出宽阔的带隙. 这一带隙被横波色散曲线分成若干个较窄的带隙. 但在透声损失曲线中, 超材料在纵波带隙相应的频段仍然展现出完整的隔声带. 基于有限元分析得到不同频率下该超材料内的声场分布, 如图13所示. 在耦合带隙内的大部分频率处, 波场分布与图13(a)类似, 分析可知基体中声波的半波长等于层厚度, 单元的共振模态与单元间的多重散射波发生强烈的相互作用, 入射波随着在基体内的传播而逐渐衰减. 这时每个单元都能高效反射入射波, 且不同单元产生的反射波会产生相长干涉, 最终在耦合带隙内产生高效的隔声性能. 在带隙外, 反射波不形成相长干涉, 这时介质中波场分布如图13(b)所示, 结构对入射波传播的抑制不明显. 在归一化频率 0.42 处透声损失出现一个尖峰值, 图13(c)为入射波频率恰好为此频率时超材料内部的波场, 这时共振单元会强烈的振动, 并高效的反射入射声波, 为典型的局域共振机制. 类似的, Yang 等(2019b)研究了一种由声学空腔与金属薄板构成的超材料隔声结构, 通过能带结构与波动模态分析, 发现其同样存在两种带隙特性. 通过局域共振和布拉格隔声频带的耦合设计, 可以增强单元共振模态和多重散射声场之间的相互作用, 进而拓宽隔声的频段, 同时增强其衰减程度.

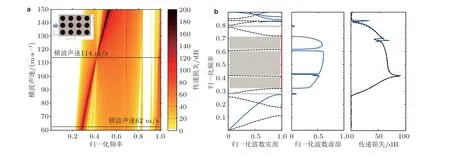
图12球形多层局域共振力学超材料的传声特性. (a) 透声损失 (TL) 随包覆层横波声速 (cCS) 变化的频谱图, (b)带隙耦合时的能带结构和透声损失频谱

图13球形多层局域共振力学超材料不同频率下的声场分布

除了带隙耦合的工作频带展宽方式, 在力学超材料设计中引入梯度单元(Zhang et al. 2013a)、负泊松比单元(Wang et al. 2015, Zhang et al. 2013b)、阻抗渐变的多层材料(Tao et al. 2010)、轻质强各向异性单元(Chen et al. 2020)等, 也可以实现低频性能的提升. 最近, 通过主动有源系统调节声-结构耦合关系从而提升隔声去耦性能的相关研究也得到关注, 如He 等(2019, 2020a,2021)设计了基于声-固耦合结构表面加速度和位移反馈参数的主动控制系统, 对力学超材料等效参数进行动态调节, 从而实现结构声透射和辐射特性的灵活控制. 需要指出的是, 目前关于去耦材料的相关研究工作大多不考虑材料应用的实际边界条件和载荷条件, 但面向工程应用, 这些问题需要得到进一步关注. 如静水压力、背衬条件等因素对材料去耦性能的影响规律, 冲击、爆炸等特殊激励条件下材料去耦设计等问题, 将成为去耦材料研究的重要方向.

3.3 水声引导材料设计

基于吸、隔声原理的水声调控会无法避免的留下“声影区”, 难以对抗多基地声呐探测等多方向立体探测技术. 利用力学超材料引导声波沿特定路径传播来控制声散射特性的思路可以实现对探测声波的全方向、高自由度控制和透明化隐身, 成为水下声隐身领域发展的热点之一.

通过设计材料参数在空间位置按特定规律变化, 从而引导波沿特定的、预先设定的路径传播是绕射声隐身的基本实现思路. 在这一方面, 变换声学是最具代表性的设计理论. 2006 年英国帝国理工大学Pendry (2006)提出基于空间坐标变换的电磁波调控理论, 从设想的波传播轨迹解析的反推所需要的材料参数空间分布, 为引导波沿任意弯曲路径传播的非均匀材料设计提供了一般性的理论. 该理论能够设计控制电磁波绕过目标物体而不产生散射的隐身斗篷 (如图14 所示) , 引起了众多研究者的关注. 该理论很快被引入声波控制领域, 发展了变换声学理论(Cummer & Schurig 2007). 2006 年美国犹他大学Milton 等(2006)研究了弹性波方程在坐标变换下的形式, 得到表达为一般性张量形式的各向异性弹性介质参数. 杜克大学的Cummer 等(2008)以及香港科技大学Chen 和Chan (2007)分别证明了二维、三维标量声波方程满足坐标变换的形式不变性, 论证了变换声学设计的可行性, 提出声隐身斗篷设计的理论模型. 这些模型均由材料参数大范围梯度变化的强各向异性非均匀介质构成, 其结构设计与物理实现是极具挑战性的问题.

虽然研究者很快提出了基于多层各向同性介质设计各向异性密度的类流体介质的思路(Cheng et al. 2008), 但材料参数随位置连续变化的要求不利于制备, 使得引导超材料的结构设计与实验验证方面进展相对缓慢. 研究者探讨了利用流体叠层(Flores-Méndez & Pérez-Rodríguez 2013)、穿孔板(Popa et al. 2016)等多种单元结构来打破速度的连续性实现各向异性等效密度. Zhang 等(2011)基于等效声学电路分析模型, 利用沿径向梯度变化的亥姆霍兹共振腔单元阵列模拟梯度变化的各向异性流体介质, 在52 ～ 64 kHz 的超声频段实验证实了变换声学介质基于引导控制原理的声隐身效果 (图15(a)) . 基于变化声学设计的灵活性, 研究者进而提出了地毯式隐身结构、弯曲声波导等设计模型. 中科院声学研究所Bi 等(2018)基于叠层板模型设计制备了水下声隐身地毯, 将不平表面的散射波引导为光滑平面的散射波, 同样实现透明化声隐身的效果 (图15(b)) . 这些研究都是基于流固混合复合结构来模拟各向异性渐变流体介质, 不利于应用于水下工程实际. Norris (2008)基于各向异性弹性模量的变换声学理论, 提出利用五模力学超材料实现声隐身斗篷的设计思路. 五模力学超材料为全固体介质, 通过结构设计能够实现等效剪切模量远小于压缩模量的力学结构, 从而模拟流体的力学、声学特性, 且采用非谐振设计, 有利于拓宽控制带宽, 因而在工程上更具有应用价值. 五模水声超材料的设计制备很快取得突破, 2013 年, Norris 和Hladky-Hennion (2013)报道了二维五模超材料水声负折射原理试验件的测试结果, 随后Bückmann 等(2014)开展了三维五模超材料的设计与制备工作. 在此基础上,北京理工大学胡更开课题组(Chen et al. 2017a) (图15(c)) 、武汉第二船舶设计研究所(Zhao et al. 2017a)等报道了基于五模材料的声隐身斗篷原理验证结果, 中科院声学研究所Sun 等(2019)提出了基于五模材料的水下声隐身地毯设计 (图15(d)) . 以上工作表明, 五模材料已逐渐成为水声引导超材料的主要实现途径. 关于五模力学超材料斗篷的微结构设计、声波调控机理、制备与实验验证等, 陈毅等 (2016)进行了专题综述, 本文不再详述.

图14隐身斗篷的波绕射控制及隐身效果示意图

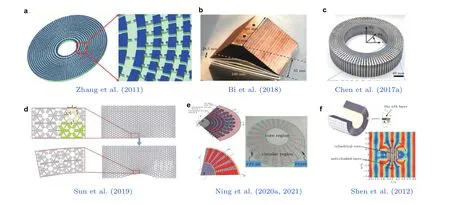
图15基于波引导力学超材料的隐身斗篷和隐身地毯结构

传统隐身斗篷工作频段相对固定, 无法随入射波频率的变化而灵活调节. 为了解决这一问题, 研究者提出将主动控制系统引入力学超材料设计, 从而实现波引导的主动、自适应控制.Ning 等(2020a, 2021)利用丙烯腈-丁二烯-苯乙烯 (ABS) 、聚二甲基硅氧烷 (PDMS) 和压电(PZT) 贴片交替排列的方法设计了具有各向异性结构的弹性波斗篷 (图15(e)) , 压电材料连接主动控制系统用以调节等效弹性模量, 实现并通过实验验证了该斗篷超宽带特性和带宽可调的功能. 在主动声隐身斗篷研究基础上, 研究者还提出基于隐身结构反向设计实现固体弹性波黑洞的主动控制(Ning et al. 2020b), 或是实现如图15(f)所示的水声隐身 “反斗篷”设计(Shen et al.2012). 这些研究工作进一步扩展了力学超材料在水声精确调控方面的应用范围.

在变换声学之外, 基于广义Snell 定律及惠更斯-菲涅耳原理的声学梯度超表面也是引导超材料研究关注的热点, 它通过在两种介质的界面上设计声学、力学特性随位置逐渐变化的亚波长弹元实现弹性波的调制. 基于相位梯度这一新的波场控制自由度, 它可以实现任意角度的声折射、声聚焦、指向性声发射等声波引导功能. 2013 年, Li 等(2013)将超表面的概念引入到力学超材料研究领域后, 南京大学Tian 等(2015)研究了利用五模材料构造水声超表面引导声波的问题, 对水声超表面的相位梯度设计、阻抗匹配等问题进行了探讨 (如图16 所示) . 最近, 研究者还研究了基于五模水声超表面的反常折射(Cai et al. 2017)、反射及吸声增强(Cai et al. 2018)等效应. 利用单层结构就可以灵活的引导声波传播的特点使得超表面对水下声控制及声隐身工程应用具有极大的吸引力. 考虑实际工程边界和载荷条件的结构设计、宽频带的声波控制、以及高效、低成本的制备是其应用于水声工程需要面对的挑战性问题.

4 空气声调控特性及降噪应用

相比水声调控, 空气声控制的需求更加普遍. 随着工业、运输业的飞速发展和城市化进程的加快, 现代社会几乎人人都受到噪声的影响, 噪声污染已成为三大环境污染之一; 在军事和工业领域, 噪声问题不仅影响人员的舒适性和健康, 强噪声还会降低仪器设备的精度和可靠性, 因此噪声控制技术得到广泛应用. 当前, 在工程约束条件 (质量、尺寸、材质等) 下, 实现低频噪声的有效吸收或隔离是这一领域的主要挑战和研究热点. 特别是近年来, 高铁、飞机等大型装备不断向高速、重载、轻质等方向发展, 其所面临的噪声问题也愈显突出, 特别是低频噪声, 往往量级大、能量高、传播距离远, 传统噪声控制手段难以解决. 在这样的背景下, 人们自然提出将力学超材料的亚波长波控特性与吸声、隔声、消声等传统技术相结合, 重点突破低频应用局限.

4.1 吸声力学超材料

材料吸声性能通常采用吸声系数来描述, 定义为吸收声能量与入射总声能之比. 当声波以φ的角度入射至吸声材料表面时, 吸声系数可以用介质界面上的法向输入阻抗来表示

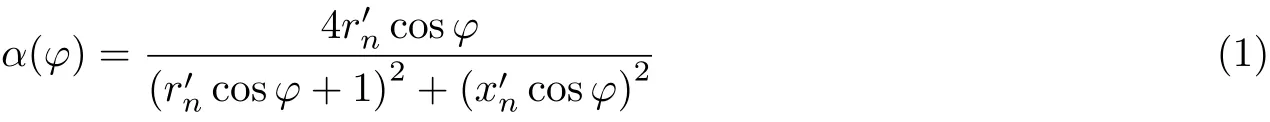
采用多孔性材料进行声学处理是最常用的吸声降噪措施. 多孔材料中具有大量连通孔隙, 声波入射至材料表面时, 部分能量进入多孔材料, 引起内部空气振动, 由于材料中空气与孔的摩擦和黏滞阻力等, 将部分声能转化为热能. 此外, 声波在多孔材料曲折的孔隙中传播并经过多次反射能量得到进一步衰减. 多孔材料通常具有复杂的材料参数和内部几何形状, 难以建立确定性模型进行分析求解. 因此, 在分析中通常采用空间等效参数模型, 如其波传播方程可以表达为

图16基于梯度超表面的(a)水声引导折射与(b)聚焦效应

其中s为曲折因子, 评价声波在曲折空间中传播的路径长度, 反映了材料几何结构对流体有效速度的影响;h为孔隙率, 是吸声材料连通空气体积与材料总体积的比值;r为流阻, 评价吸声材料对空气黏滞性影响大小的参量. 对于半无限大多孔吸声材料, 其法向输入阻抗比为

其中定义无量纲频率Ω=ωρ0s/(rh) . 由式(1)和式(3)可以得到多孔材料吸声系数. 如考虑垂直入射 (φ= 0fl) , 在低频和高频段, 可以分别近似表达为

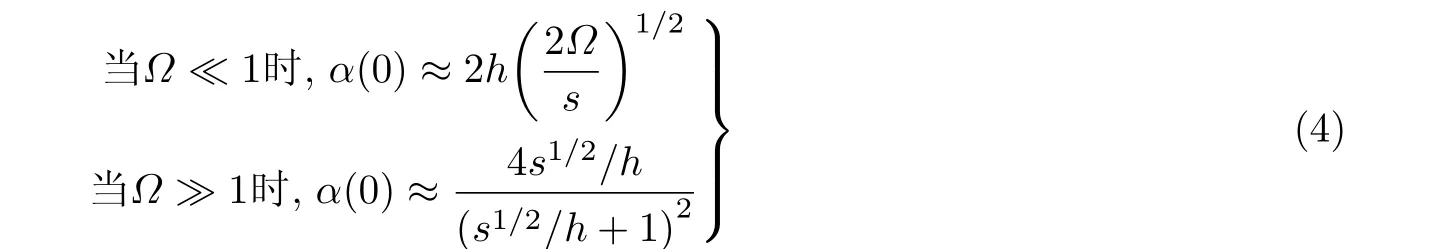
由式(4)可知, 在低频段, 吸声系数与ω1/2成正比, 吸声系数随频率降低而迅速下降, 在高频段, 吸声系数趋于恒定值, 吸声性能与曲折因子和孔隙率相关.

对于贴覆在刚性 (近刚性) 表面上的有限厚度吸声材料, 其吸声系数同样可以求得

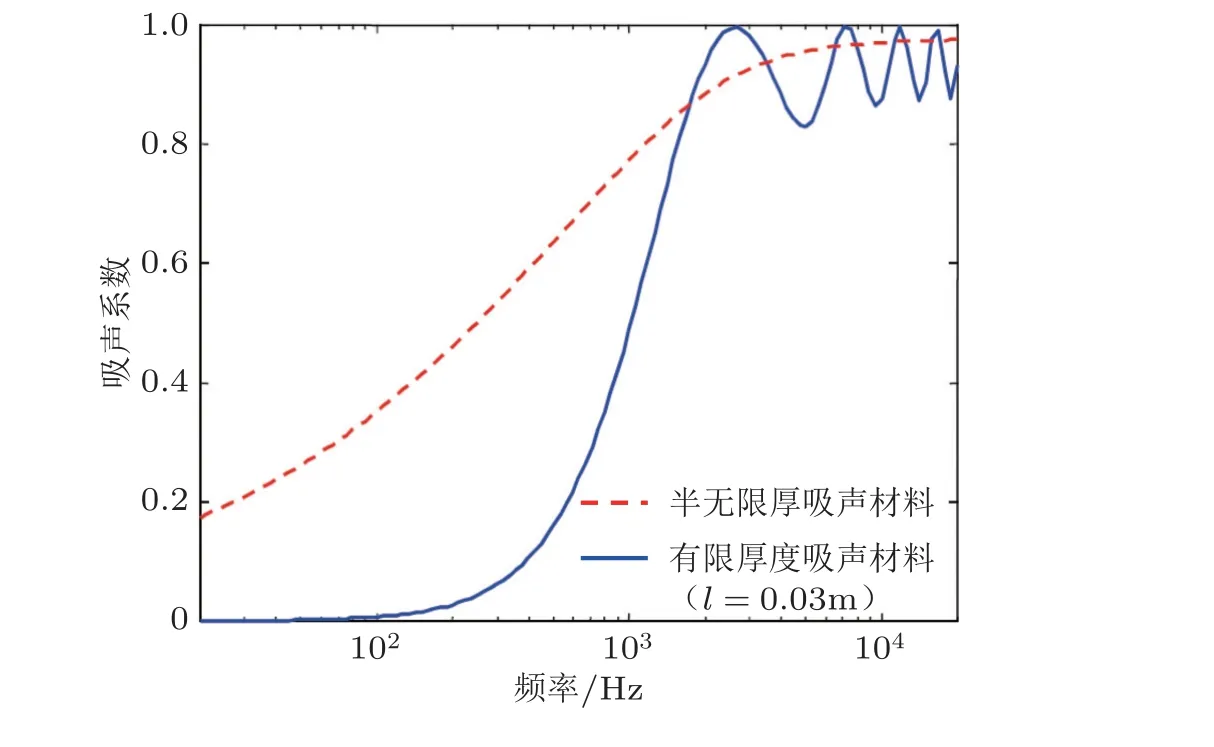
图17典型多孔材料吸声性能 (h = 0.9, s = 1.5, r = 3.0×104 rayls/m, l = 0.03 m)

其中l为材料厚度. 图17 比较了有限厚度和半无限大多孔材料垂直入射下的吸声性能. 在低频段, 有限厚度材料吸声系数与ω2成正比, 比半无限介质吸声系数随频率降低下降速度更快, 吸声性能更差. 在高频段, 有限厚度材料吸声系数在式(5)得到的结果附近波动, 平均吸声性能与无限介质相当. 因此, 多孔材料主要工作在高频段, 其吸声性能取决于材料参数. 在低频段, 无论是无限厚度还是有限厚度, 材料吸声系数均较低, 如果要提高低频吸声性能, 则需要增大其厚度.多孔吸声材料厚度每增大1 倍, 最大吸声频率约向低频移动一个倍频程. 要实现有效吸声, 材料厚度应至少大于最低吸收频率对应波长的四分之一, 因此低频吸声所需材料厚度较大(Allard &Atalla 2009).

为了增强材料低频吸声性能, 研究者提出了具有共振效应的吸声结构. 传统吸声结构包括亥姆霍兹共振腔结构(Kim et al. 2006)、穿孔/缝板(Maa 1998)、薄板等. 吸声结构的等效声阻抗可以表示为

近年来, 力学超材料也逐步被引入低频吸声设计中, 以局域共振型薄膜、空间卷曲亥姆霍兹共振腔、空间卷曲Fabry-Pérot (FP) 腔为代表的吸声力学超材料得到广泛关注.

2008 年, 香港科技大学Yang 等(2008) 提出了薄膜型声学超材料的概念, 其结构单元一般采用框架结构固定张紧的弹性薄膜, 并在薄膜上布置质量块. 这一工作从理论及实验上发现了薄膜型超材料具有低频隔声特性, 随后, 研究人员发现, 这类薄膜超材料同样可以实现低频吸声特性.Mei 等(2012)设计了一种附加非对称质量块的双层薄膜吸声超材料 (薄膜间距28 mm) , 结构见图18(a). 研究表明, 在刚性背衬条件下 (刚性背衬与薄膜材料间存在28 mm 空腔) , 超材料在100 Hz 到1000 Hz 频段上可形成若干吸收峰, 见图18(b), 其吸声峰最低频率为164 Hz, 材料整体厚度 (约56 mm) 与该吸声峰处波长之比约为1/37. 质量块周边存在较大弯曲变形及其引起的能量耗散, 是亚波长频段有效吸声的主要机制. Ma 等(2014)提出了一种耦合共振薄膜型声学超材料结构, 结构见图18(c). 该薄膜结构构造的内部封闭空腔形成耦合共振 (hybrid resonance) .在刚性背衬条件下, 该薄膜型声学超材料总体厚度与共振吸声频率波长之比可以达到1/133. 耦合共振导致样品输入阻抗与空气介质匹配, 且由于薄膜的大弯曲变形以及约束效应获得深亚波长频段的高效吸声. 在此基础上, 研究者考虑不同边界条件, 得到了薄膜超材料获得完美吸声性能的条件(Yang et al. 2015, Duan et al. 2015).

在空间卷曲超材料方面, Li 等(2016)设计了具有平面卷曲腔体的亥姆霍兹共振力学超材料,这一超材料厚度与吸声峰波长之比小于1/200. 随后, Wang 等(2017a)设计了一种卷曲亥姆霍兹超材料 (见图19), 发现了在不改变超材料整体厚度的条件下, 通过调节空间卷曲通道宽度, 可有效调节吸声带宽, 这一结论得到了实验验证. 这一现象在后续工作中得以进一步验证(Shen et al.2019). 阻抗、场图以及复频率平面反射系数分析表明, 共振频率处超材料与空气完美临界耦合且阻抗匹配, 进而穿孔内强黏性摩擦耗散是其低频完美吸声的主要机理.

在空间卷曲Fabry-Pérot 超材料研究方面, 由于Fabry-Pérot 超材料需要通道长度约是共振频率处声波波长的1/4, 通过空间卷曲结构可延长通道长度, 从而降低其吸声频率. 声波通过与Fabry-Pérot 共振腔壁面的黏性摩擦被耗散, 产生声波耗散. 在腔壁声波耗散能力不足时, 可在通道口或者通道内部添加泡沫材料增加耗散. Cai 等(2014)将空间卷曲结构引入到Fabry-Pérot 型力学超材料吸声研究中, 在400 Hz 处获得了低频吸声峰, 并得到了实验验证. 随后, 研究者针对Fabry-Pérot 型力学超材料吸声调谐(Zhang & Hu 2016, Liu et al. 2017)、多单元宽频吸声设计(Yang et al. 2017, Chang et al. 2018)等方面开展了研究. 除了上述工作外, 吸声超材料研究还包括通风型吸声材料(Li et al. 2018, Kumar & Lee 2020, Kumar et al. 2020, Mao et al. 2021)、缝隙型吸声材料(Wu X et al. 2016, Zhao et al. 2018a, Lau et al. 2021)、非对称型吸声超材料(Liu &Jiang 2018, Lee et al. 2020, Long et al. 2020)等.

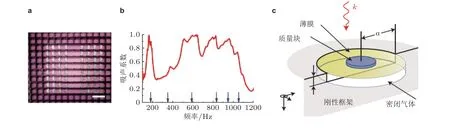
图18(a)薄膜型力学超材料及其(b)吸声性能(Mei et al. 2012), (c)耦合共振薄膜型力学超材料结构单元(Ma et al. 2014)

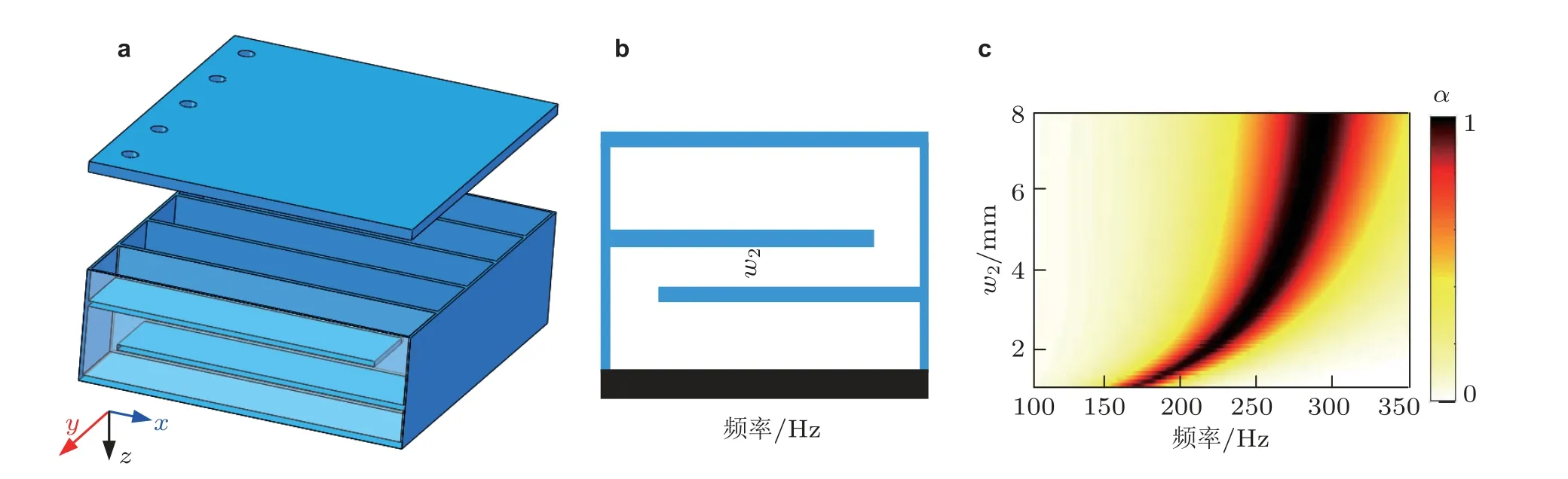
图19(a)空间卷曲力学超材料及其(b)单元结构和 (c)吸声调谐规律(Wang et al. 2017a)

在单一机理力学超材料研究的基础上, 基于多机理耦合可以有效拓宽吸声带宽. 如Wu 等(2019)将微穿孔板与空间卷曲结构复合(见图20(a)), 研究结果表明, 在5 cm 薄厚度下, 超材料在500 Hz 以下的低频范围内归一化吸声带宽高达82%. 进一步, (Zhao H et al. 2020)设计了如图20(b)所示的空间卷曲结构与传统多孔材料复合的并联结构. 由于卷曲通道的多阶共振, 能够在低频段产生完美吸声峰; 利用多孔材料的阻尼效应, 超材料同时还能够对中高频段声波进行有效吸收.此外, 关于不同形式结构单元复合方面的研究近年来也方兴未艾: 例如微缝与亥姆霍兹共振腔(Jiménez et al. 2016), 内插管亥姆霍兹共振器与空间卷曲结构(Huang et al. 2019a), 泡沫与亥姆霍兹腔(Lagarrigue et al. 2013, 2016) 、空腔(Groby et al. 2011) 等结构复合. 不同结构单元通过在不同频率范围实现优势互补, 达到了有效拓宽吸声带宽的目的(Huang et al. 2019b, Liu et al.2020, Gao et al. 2021, Li et al. 2021a).

从上述研究现状可见, 超材料空气声吸声目前多聚焦于理论和机理研究, 随着研究工作的深入, 应逐步将这些新的吸声机理应用于实际装备降噪中, 即针对实际应用边界条件, 在成本、厚度以及质量等约束条件下, 综合优化设计具有良好低频、宽带吸声性能的空气声吸声材料, 从而推动理论研究成果加速应用.

4.2 隔声力学超材料

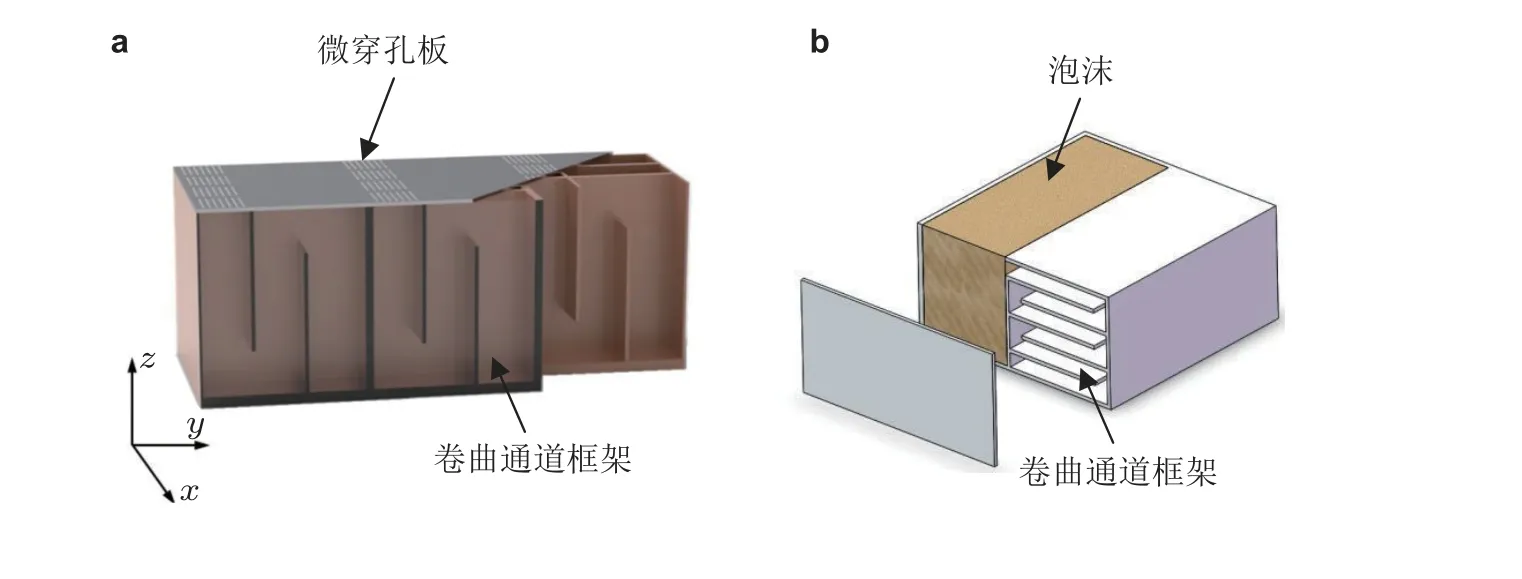
图20(a)微穿孔复合空间卷曲超材料(Wu et al. 2019), (b) 泡沫复合卷曲通道超材料(Zhao H et al.2020)

隔声是研究在结构中声传递现象的一门理论与技术, 是利用材料 (构件、结构或系统) 阻碍噪声的传播, 从而降低通过材料后噪声的能量. 隔声材料透声能力的大小, 通常用能量的透射系数来表示:τ=Et/Ei, 其中Ei为入射到隔声材料上的能量,Et为透射能量. 一般隔声材料τ通常较小, 因此工程中通常用隔声量 (也称传声损失) 来评价隔声能力

作为噪声控制最简单直接的一种手段, 隔声理论的发展已经有相当长的历史. 19 世纪末, 瑞利爵士就提出了不可压缩无限大墙的隔声理论, 并得到薄板的“质量定律”(Rayleigh 1896). 对于空气介质中单层均质无限大薄板, 在声波垂直入射条件下其隔声量可以近似表示为

式中,ω为角频率,ρ和h分 别 为 材 料 的 密 度 和 厚 度,ρ0c0为空气的特性阻抗. 可 见, 隔 声 性 能 与材料、结构、声波频率有关. 从式(8)可见, 材料面质量增大一倍, 隔声量增大6 dB, 或增大一个倍频程, 隔声量增大6 dB, 这就是薄板隔声的质量定律. 尽管这一结论是建立在诸多假设基础上得到的结果, 但时至今日, 仍是隔声研究和工程应用最重要的原则之一. 质量定律表明, 提高均质材料的隔声性能往往需要通过增大材料厚度或密度来解决, 这与当前结构轻质化的发展趋势相矛盾. 实现轻质薄层下的高效隔声是工程领域始终关注的热点.

1995 年, 西班牙学者观察到一座具有200 多年历史的雕塑“流动的旋律”具有阻隔特定频率范围声音的现象(Martinez-Sala et al. 1995) (如图21(a)) . 实验角度验证了周期结构的带隙特性. 这一工作推动了声子晶体概念的产生, 也为声子晶体用于隔声设计提供了原始思路. Sánchez-Dehesa 等(2011)基于传递矩阵和多重散射法, 系统研究了由圆柱散射体构成的声子晶体的声传播特性 (如图21(b)) , 并提出将其应用于隔声屏障设计. Garcia-Chocano 等(2012)进一步将这类声子晶体与微穿孔吸声结构结合, 实现了宽频带的噪声阻隔和吸收 (如图21(c)) . 声子晶体可以实现带隙的灵活调控, 但其带隙可设计频率受晶格尺寸限制, 很难实现小尺寸条件下的低频波控特性. 力学超材料为突破低频设计提供了设计源泉, 进一步围绕工程中轻质、薄层应用需求,目前研究主要集中在薄膜型和薄板型力学超材料.

图21二维声子晶体隔声结构. (a) 雕塑隔声结构 (Martinez-Sala et al. 1995), (b) 二维声子晶体示意图,(c) 声子晶体隔声屏障 (Garcia-Chocano et al. 2012)

上节介绍的薄膜型吸声超材料同样具有低频超常隔声性能, 其隔声机理是利用微结构单元在声波激励下的反共振特性形成对入射声波的强反射, 实现远高于质量定律的隔声量Yang 等(2008) . 基于支撑框架固定不动和忽略附加重物刚度和尺寸两个假设条件, Zhang 等(2012)建立了薄膜超材料隔声特性的解析模型并深入分析了薄膜超材料的隔声机理和调控规律. 以图22(a)中所示的方形薄膜超材料元胞为例, 通过解析计算可以得到的超材料的隔声曲线 (实线) . 发现其在低频段存在一个隔声峰, 同时有两个隔声低谷. 进一步通过相位曲线 (点画线) 可以看到在特征频率 (隔声曲线隔声峰和隔声谷所对应的频率) 处相位发生翻转, 说明透射声压的传播方向发生了改变. 薄膜型力学超材料的隔声量与质量密度定律式(8)所预测的同质量均质板隔声量相比, 低频隔声特性得到了明显的提高, 特别是在隔声高峰的频率位置处, 整个薄膜型力学超材料的隔声量远大于均质板的隔声量.

由声振耦合关系可知, 透射声压是由薄膜透射面的振动引起的, 相位的翻转, 表明薄膜的振动模态的改变. 如图22(b)所示, 两个隔声谷对应两个本征共振频率: 在第一隔声谷处, 整个结构的振动主要集中在质量块附近; 在第二隔声谷处, 整个结构附加重物处的横向位移几乎为零,位移主要集中在薄膜的四周. 在两个相邻的共振模态之间产生一个反共振模态, 此时质量块附近的位移与薄膜四周处的位移反相, 通过在整个面上叠加, 得到整个结构的振动位移等于零. 由此可以发现, 在共振频率附近, 共振模式导致材料透声能力增强而产生隔声低谷; 在反共振频率附近, 相邻共振模式的反相叠加导致材料与入射声波几乎没有耦合作用, 使入射声波完全反射, 形成隔声峰. 通过计算动态等效质量密度 (见图22(c)) 可以进一步看到, 随着频率增大, 等效质量密度在第一隔声谷位置 (平均位移最大处) 由正变为负, 然后在隔声峰处由负跳变为正, 最终在高频处趋近于整个系统的面平均值. 整个薄膜平面的平均位移在两个隔声谷频率处取最大值, 在隔声峰频率处接近为零. 另一方面, 等效质量密度的绝对值在隔声峰处极大, 就好像整个系统的质量密度突然提高了一样, 隔声效果也就得到了提高.

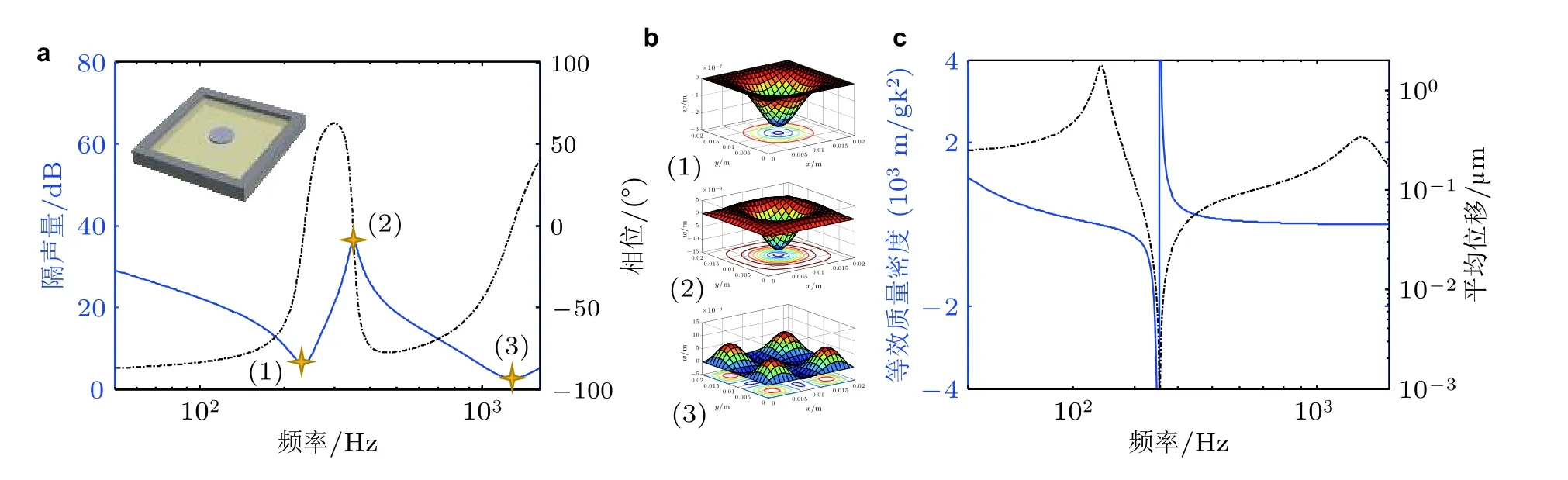
图22薄膜力学超材料的隔声特性. (a) 隔声曲线及相位曲线, (b) 隔声峰谷模态振型, (c) 动态等效质量密度和膜结构平均位移曲线(Zhang et al. 2012)

总体来说, 由于重物与薄膜密度的巨大差异, 使得整个薄膜型力学超材料表现出两种本征振动模态. 其中, 第一种本征模态是由于重物与薄膜组成的弹簧质量系统局域振动引起的, 第二种本征模态是由于重物与边界之间薄膜自身共振引起的, 这两种本征模态相互独立. 当入射波频率大于第一种本征模态频率时, 重物与薄膜组成的弹簧质量系统振动反相, 使得整个材料的隔声性能提高.

对于单振子单元的薄膜超材料, 其增强的隔声性能只能在反共振频率附近很窄的频段内获得, 如何获得更宽的工作频段同样是薄膜隔声超材料研究的重点. Zhang 等(2013c)设计了如图23(a)所示的超材料单元, 基于多频共振机理, 通过在相邻元胞内附加不同的质量获得多个隔声峰. Lu 等(2020)研究了附加质量块的形状和位置对隔声性能的影响 (如图23(b)) , 发现通过优化设计, 可以实现隔声频段的拓宽. 基于这一思路, 通过设计附加质量的形状和排布方式更为复杂的超材料元胞, 可以进一步提升了薄膜超材料的隔声性能(Naify et al. 2011, Zhou et al.2020). Yang 等(2010)通过将多层薄膜超材料叠加, 实现了50 ～ 1500 Hz 范围内的宽带声衰减(如图23(c)) . Ang 等(2017)在研究如图23(d)所示的大尺度薄膜超材料隔声性能时发现, 隔声性能还受到框架结构振动的影响, 此时, 元胞理论模型中框架固定不动的假设不再成立. 通过优化框架结构参数设计, 可以实现低频隔声频段的拓宽. Wang 等(2019a)将大尺度薄膜超材料与多频共振进行了集成设计, 在500 Hz 频段以下得到高于质量定律的隔声效果 (如图23(e)) .

在薄膜超材料设计中, 弹性薄膜通常选用高分子橡胶材料, 以实现局域共振系统具有低刚度. 这使得薄膜隔声材料在工程应用中可能存在一定得局限性, 如环境 (温度、湿度等) 条件变化会导致膜特性变化而影响材料声学性能. 此外, 薄膜张紧力也与声学性能紧密相关, 在大尺度薄膜超材料中实现张紧力的精确控制也具有一定难度, 使得这类超材料制备比较困难. 因此, 工程中更倾向于在装备原有板壳类结构的基础上进行隔声设计.

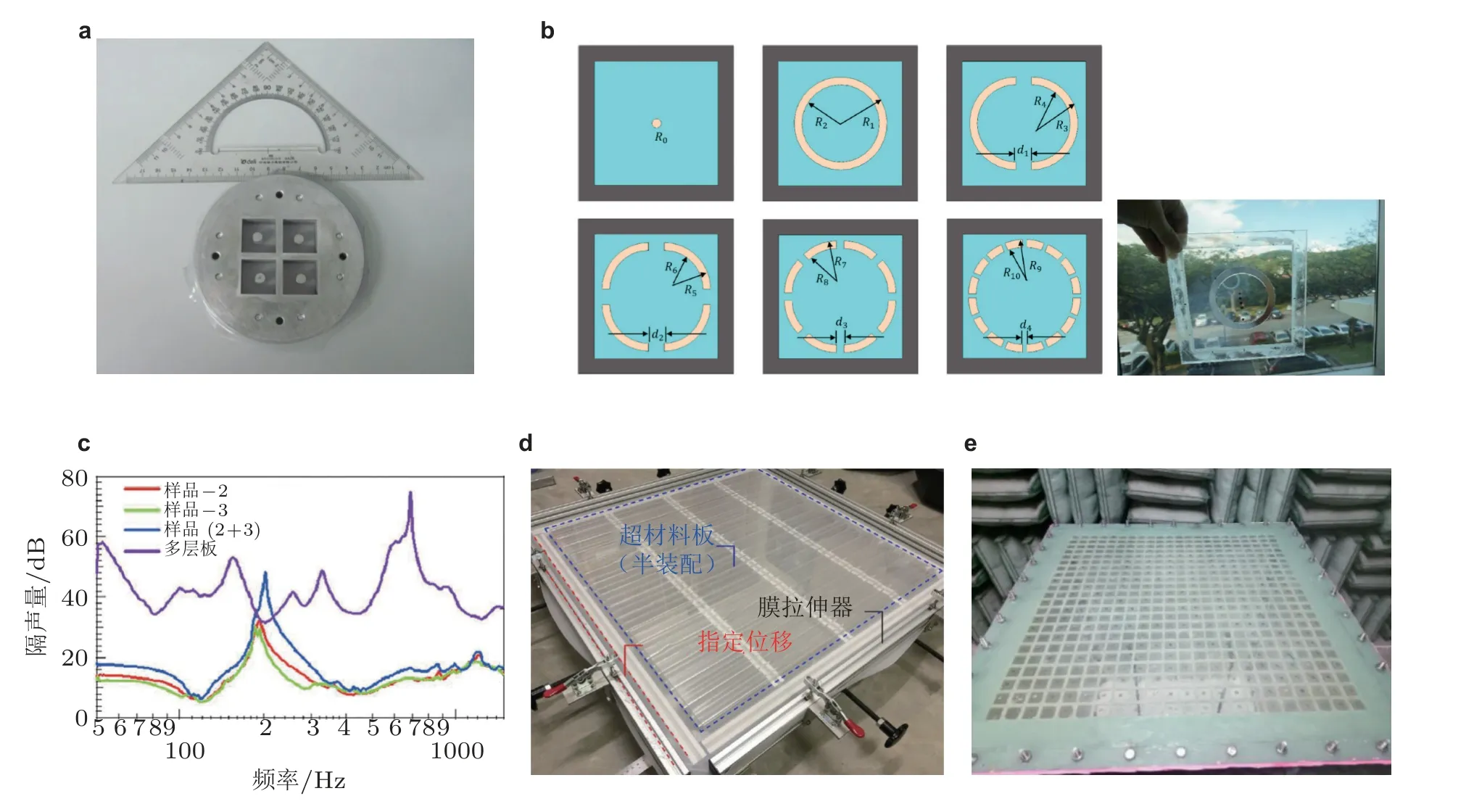
图23薄膜型隔声力学超材料. 结构设计来自文献(a) Zhang et al. (2013c), (b) Lu et al. (2020), (c)Yang et al. (2010), (d) Ang et al. (2017), (e) Wang et al. (2019a)

20 世纪90 年代中期, Hashimoto 等(1991)在较大尺寸的薄板表面周期性附加金属重物, 实验研究发现, 在低频的某些频段, 该结构具有远超同质量薄板隔声量的优良性能. Xiao 等(2012a)通过在薄板上周期性附加局域共振子, 构造了一种板状超材料, 如图24 所示, 发现其可以在低频范围打破隔声质量定律的限制, 实现远高于同质量均质板的隔声量; 此外还发现, 通过合理调控局域共振频率, 可以抑制板结构的吻合效应, 大幅提高板结构在吻合效应区的隔声量.Song 等(2015)将板状超材料设计思想进一步引入到蜂窝夹层板设计, 在蜂窝夹层板上周期性附加由软橡胶和硬铝制成的局域共振子, 构建了一种板类隔声超结构, 通过理论分析、仿真模拟计算发现, 该超结构在中高频段能获得相比同等质量蜂窝板更好的隔声效果.

de Melo Filho 等(2019)设计了一种在单层薄板上周期性附着经过特殊设计的局域共振子的双层薄板型声学隔声超材料, 如图25(a)所示, 该隔声超材料在500 Hz 附近的频段具有较理想的隔声效果. Langfeldt 等(2020)等设计了一种内含亥姆霍兹共鸣器的双壁板超材料, 如图25(b)所示, 通过调整共鸣器的谐振频率, 有效改善了双壁板结构低频区的隔声性能, 并利用内含亥姆霍兹共鸣器的流体介质的等效参数, 建立了一种分析模型, 可以有效地描述含亥姆霍兹共鸣器的双壁板结构的隔声特性.

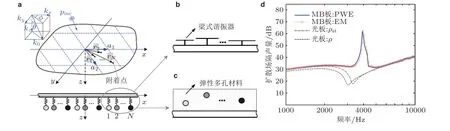
图24周期性附加局域共振子的板状力学超材料(Xiao et al. 2012a)

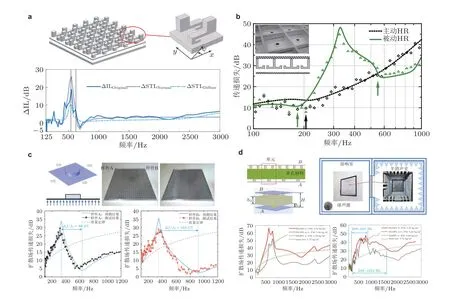
图25板状力学超材料的隔声设计. (a) 附着局域共振子的双层板状力学超材料(de Melo Filho et al.2019), (b) 内含亥姆霍兹共鸣器的双层板状力学超材料(Langfeldt et al. 2020), (c) 轻质薄层板状力学超材料 (Xiao et al. 2021a), (d) 含多孔材料层的双层板状超材料(Wang et al. 2021)

Xiao 等(2021a)针对由薄板上周期性附加质量块构成的轻质薄层板状隔声超材料展开了系统研究. 他们考虑的隔声超材料如图25(c)所示, 针对其隔声性能计算提出了一种半解析计算方法, 可以高效准确地预测板状超材料的隔声量. 该方法基于一种简化的结构有限元模型, 可以无需考虑声场, 快速反演动态表面质量密度. 同时, 研究了拓宽该结构隔声带宽的规律, 在低频宽带隔声领域有广阔的应用前景, 通过进行大样实验, 验证了拓宽隔声带宽的规律的有效性. Wang等(2021)进一步设计提出了内含多孔材料夹层的双层板状超材料. 如图25(d)所示, 通过引入多孔材料可以极大地改善双层板状超材料的斜入射及扩散声场条件下的隔声性能, 大样实验研究表明, 其在248 ～ 1624 Hz 的低频超宽带范围深度打破质量定律, 并且在208 ～ 850 Hz 的低频宽带范围内隔声性能显著优于同质量的内含多孔材料的双层均质板结构. 同时, 提出了基于半解析法的双层板状超材料隔声量的计算方法, 并且验证了其有效性, 为双层板状超材料设计阶段的高效计算提供了途径.

传统的隔音结构通常会阻止结构两边的流体传输, 但在一些特定的工程应用条件下, 希望结构既具有隔声性能, 还能保持一定的空气流动性. 杜克大学Cummer 团队设计了由开放空气通道和分流亥姆霍兹共振单元构成的声学梯度超表面, 并基于此构造了具有反射阻隔任意角度入射声波的二维超构声笼(Shen et al. 2018). Liu 等(2021a)基于声学迷宫结构和各向异性的概念, 实现了低频、宽带带隙, 并设计了空间三维超构声笼, 具有深亚波长频段下的隔声性能. 这些工作为特殊工程条件下的隔声设计提供了思路.

4.3 管路消声力学超材料

舰船等大型装备内部有着非常复杂的管路系统, 通过传递能量流、动量流或质量流完成特定功能. 管路噪声主要来自管壁结构振动噪声和管内流体噪声, 管路噪声将直接影响与之相关的装备的安全性和可靠性, 影响工作人员居住环境的舒适性, 危害其身体健康, 尤其是低频噪声,携带能量较大、线谱明显、传播距离较远, 对装备的隐身性和生命力构成直接威胁(王艳林等2008, 许浩和李邦华 2018).

为有效降低管路噪声, 在管路系统安装消声器是目前最为常用的方法. 消声器结构简单, 价格便宜, 经过精心设计的消声器可以在低、中频段取得良好的消声效果, 而且消声器还有耐高温、耐腐蚀、耐高压等优良特性. 消声器根据其消声原理的不同, 可以分为阻性消声器、抗性消声器以及阻抗复合型消声器, 不同的消声器的有效消声范围不同(季振林 2016). 传统管路消声器难以实现低频宽带噪声抑制, 如共振腔式消声器虽然可以在较低频带内实现高效声衰减, 但其消声频带窄, 难以应用于变频、宽带噪声问题; 扩张式消声器虽然在中高频段消声效果较为明显, 但受安装空间限制, 低频效果有限. 突破管路系统在工程约束下的低频宽带噪声抑制问题具有重要意义和工程价值, 相关研究方兴未艾. 近些年来, 随着力学超材料在结构减振降噪方面研究的不断深入, 把超材料的设计思想应用于管路噪声控制得到了广泛的关注(吴九汇等 2016, 丁昌林等2018).

亥姆霍兹共振器 (Helmholtz resonator) 是一种最典型的消声器, 其本质上是一种声学共振单元. 基于局域共振力学超材料亚波长波控特性, 将亥姆霍兹消声器在管路中周期排列, 就可以构造超材料管路系统, 并利用带隙特性进行噪声控制. Fang 等(2006) 在研究周期附加亥姆霍兹消声器的充液导管中的波传播特性时, 发现了局域共振带隙内的负等效体积模量特性, 也验证了超材料管路的声抑制效果, 如图26(a)所示. 之后, 这类力学超材料系统得到了深入研究, 包括带隙形成机理(Wang et al. 2008), 带隙调控规律和亥姆霍兹单元优化设计(Wang & Mak 2014,Wu et al. 2017)等. 载流管路中有时存在高声压级噪声和高速流场环境, 这些因素会对超材料的声调控特性产生一定影响, 也是目前管路减振降噪研究的难点问题. Seo 等(2018)研究了高声压级和切向流作用下的亥姆霍兹阵列的消声性能, 发现高声压级和切向流作用下, 管路会产生非线性效应, 从而造成共振器阻抗的不连续, 之后, 利用提出的阻抗模型对管路消声器阵列进行了优化设计. Liu 等(2020b)基于经验阻抗模型, 提出了一种改进的传递矩阵法, 分析了均匀流作用下周期亥姆霍兹消声器的超材料管路的声学特性, 能带结构表明, 在局域共振带隙附近, 流速引起的阻尼会使得波矢实部不再覆盖整个布里渊区, 从而造成了声波带隙的“分支截断”. Liu 等(2020a)研究了温度变化对周期附加柔性壁管路的影响, 揭示了由温度变化引起的系统准周期性对带隙形成的影响, 如图26(b)所示. 研究表明, 随着管路入口、出口处的温度差变大, 带隙位置会向高频移动, 且对带宽造成不利的影响. 在温度的影响下, 通过设计晶格常数和结构参数可以对布拉格带隙和局域共振带隙进一步的进行调节.

周期排布亥姆霍兹共振器虽然能够利用带隙原理对管路进行噪声控制, 但是会占用较大的空间, 不利于实际应用, 研究附加结构厚度仅为控制波长几十分之一的亚波长尺度的管路消声结构成为工程领域关注的热点. 针对这一目标, Wang 等(2017b)设计了一种膜式超材料消声器, 如图27(a)所示, 通过声-膜结构耦合提高低频消声性能, 且整体结构尺寸远小于传统亥姆霍兹消声器. Ghaffarivardavagh 等(2019)提出了基于类法诺共振的横向双层超材料的概念, 设计了一种亚波长结构的大开口超材料消声器, 能够在保证通风效果的同时实现低频特定频率的噪声控制 (如图27(b)所示) . 为解决传统亥姆霍兹消声器工作频率较窄的问题, Nguyen 等(2020)基于狭缝式的亥姆霍兹单元设计了一种亚波长结构的双层消声器, 如图27(c)所示, 通过狭缝的阻尼效应将不同谐振单元的消声峰耦合起来, 最终能够在保证结构通风情况下实现0.48 ～ 0.95 kHz范围内的宽带消声特性. 类似的, An 和Lee (2021)在传统扩张腔消声器的基础上设计了一种抗性的超材料消声单元, 如图27(d)所示, 基于多频谐振效应实现消声频段的有效拓宽.

近年来, 声学超表面的波调控性能也被用于管路噪声控制, 能够进一步改进传统消声结构的工作性能. Zhao 等(2017b)设计了由亥姆霍兹消声器网络构成的反射型声学超表面结构, 如图27(e)所示, 并贴敷在HR 消声器空腔的背板之上, 结果表明, 声学超表面的存在改变了声波的传播路径, 使得消声工作频段向低频移动. Zhang 等(2017)在中空管的边界设计了一种可以改变波传播方向的超表面结构, 如图27(f)所示, 可以使得特定频率范围内的透射系数为0.

5 基于力学超材料的减振抗冲应用

机械振动广泛存在于工程结构和设备中, 有害振动会严重影响仪器设备精度、装备安全性、可靠性和使用寿命; 振动还会引起辐射噪声, 对人员健康和周围环境造成危害, 因此, 结构减振技术工程应用广泛. 当前, 大飞机、火箭、舰船、高速列车等大型装备, 为了实现低能耗、远航程、高机动、大载荷等目标, 装备结构设计采用了大量轻质、高刚度、高强度材料和结构, 然而静态力学性能设计与动态功能实现往往存在矛盾: 为满足刚度和强度性能目标, 需要约束材料和结构内部变形与相对运动, 但随着约束增强, 结构在动载荷下对波能量的耗散能力随之减弱, 难以实现同时具有高刚度和高阻尼特性, 调控结构动/静态力学特性使其兼具高刚度和高阻尼特性已经成为振动控制工程中亟需解决的瓶颈问题.

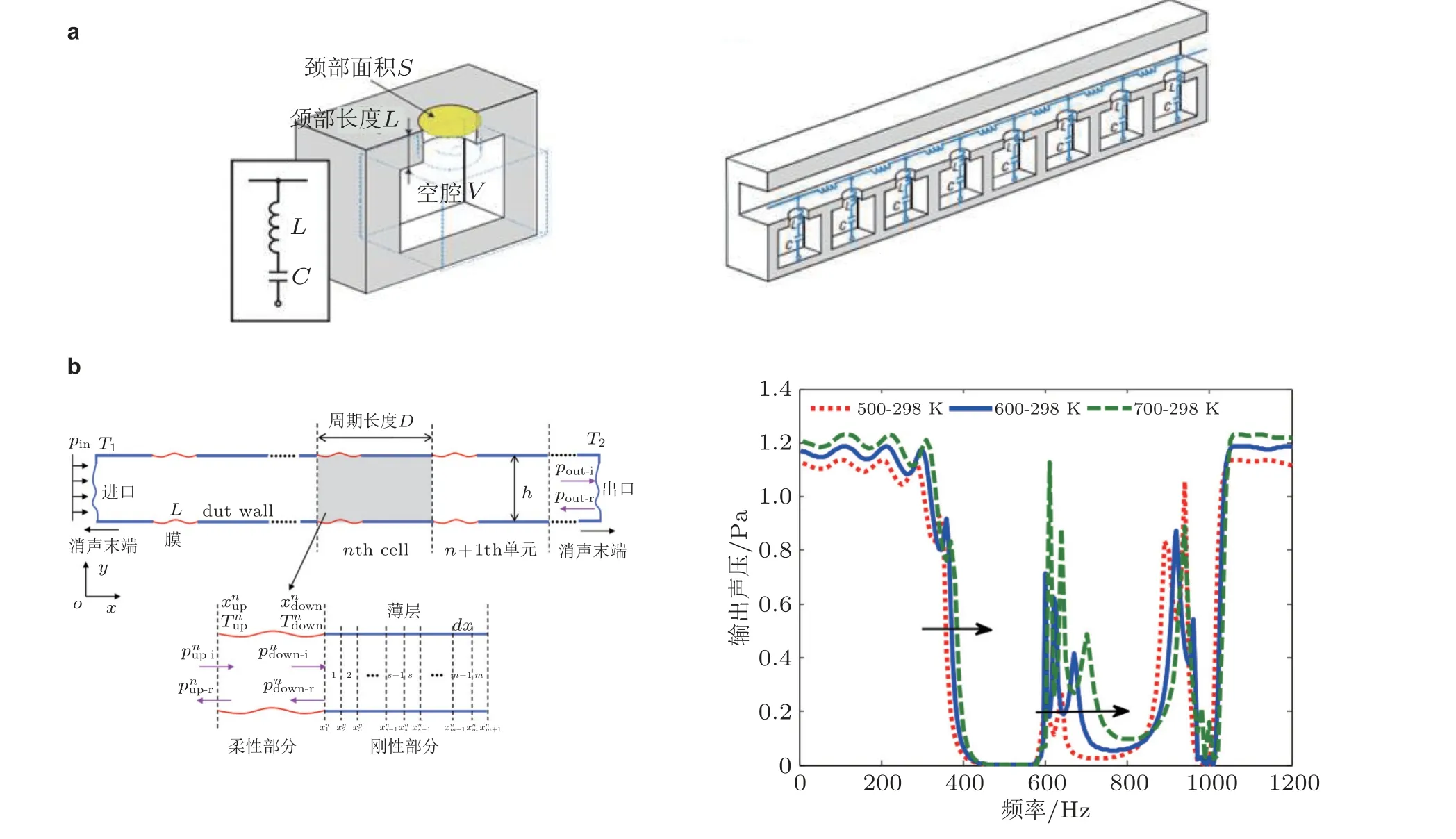
图26(a)周期排布亥姆霍兹共振器管路(Fang et al. 2006), (b)周期排布柔性壁管路 (Liu et al. 2020a)

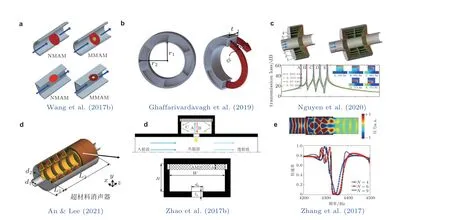
图27力学超材料管路消声结构设计

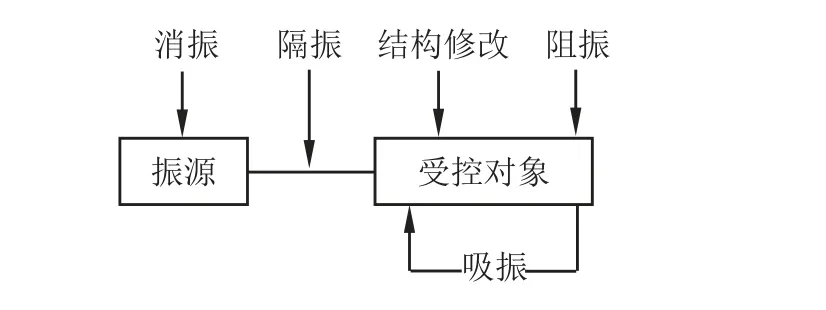
图28传统振动控制技术分类

如图28 所示, 传统振动控制技术按照作用对象主要可以分为五类: (1) 消振技术, 即消除或减弱振源, 从源头实现振动控制; (2) 隔振技术, 即在振源和受控对象之间附加隔振系统, 以减小受控对象对振源激励的响应; (3) 吸振技术, 即在受控对象上附加动力吸振器, 依靠其产生的吸振力减小受控对象对振源激励的响应; (4) 阻尼减振技术, 即在受控对象或振动传播路径上附加阻尼材料或元件, 通过消耗能量而使响应减小; (5) 结构修改, 通过修改受控对象的动力学特性参数使振动满足预定的要求, 无需附加任何子系统.

经典的减振、隔振措施(阻尼器、减振器、动力吸振器)以及黏弹性阻尼材料等振动控制技术在工程中已有广泛的应用, 但受空间、质量等工程约束条件的影响仍较大, 尤其在低频、宽带振动能量控制和耗散上存在局限性. 在结构或器件设计中引入力学超材料, 可以有效增强结构与低频波传播的耦合作用, 从而提高对波动能量的控制和耗散能力. 近年来, 相关工作主要集中在不同类型力学超材料波调控机理揭示、低频宽带减振设计 (包括带隙展宽设计、超材料元胞构型设计等) 等方面.

5.1 力学超材料低频带隙减振原理

5.1.1 带隙设计与展宽机理

从声子晶体研究起, 带隙特性就被发现可以用于结构振动控制, 其基本思想是通过设计结构参数和周期晶格参数, 将带隙范围落于待控制频段, 使波能量不能在结构中传播, 而是反射或局域在其他位置进行处理. 基于力学超材料的亚波长带隙特性开展结构减振设计研究, 首先要深入揭示带隙产生机理和调控规律.

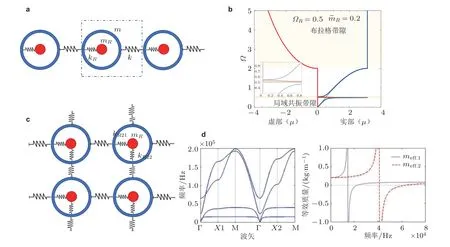
图29离散局域共振系统力学超材料模型及能带特性. (a) 一维局域共振单原子链结构, (b) 局域共振系统和原子链系统色散曲线, (c) 二维局域共振原子链结构, (d) 二维局域共振系统的带隙特性(Huang & Sun 2011)

图29(b)为局域共振系统 (实线) 和未附加共振单元的原子链系统 (虚线) 的色散曲线. 共振单元的存在使色散曲线在ΩR附近分成两支而形成带隙, 带隙的范围对应于衰减常数 (μ的虚部) 非零范围. 这一带隙与晶格系统自身波长无关, 由共振效应诱导产生, 即为局域共振带隙. 相比之下, 图中高频带隙为单原子链系统固有, 源于布拉格散射, 属于布拉格带隙. 局域共振带隙和布拉格带隙具有不同的带隙内衰减特性 (由衰减常数μ的虚部表征) : 局域共振带隙的衰减特性具有尖锐的峰值特征, 且峰值频率对应局域共振单元的固有频率; 布拉格带隙的衰减特性随频率变化较为光滑. 对于局域共振系统, 当ωR2≪ω02/2 时, 局域共振带隙的起始频率近似为ωR, 因此可以通过共振单元的固有频率估计局域共振带隙的位置. 进一步的, Huang 和Sun (2010) 研究了嵌套质量的多谐振一维原子链的带隙特性, 发现局域共振带隙内系统具有负质量特性, 揭示了内外嵌套质量对带隙的影响规律, 增加了带隙调控的自由度. 一维局域共振离散晶格也可以进一步拓展至如图所示的二维结构, 通过在共振单元的不同方向上施加不同的刚度, 可以实现材料各向异性的能带特性, 如图29(a)和(d)所示(Huang 和Sun 2011).

对于连续系统, 本文重点关注工程中广泛应用的杆、梁、板类结构. 将这些结构视为“基体”, 通过在其中周期性附加或嵌入共振单元, 可以构造局域共振力学超材料, 其带隙分析计算方法包括多重散射法、平面波展开法、有限差分法、集中质量法、有限元法等, 表1 中列举了梁板类典型力学超材料带隙解析计算方法的典型工作. 在对弹性力学超材料进行分析时, 有许多问题需要注意或值得讨论. 首先, 结构系统中通常存在多种模式波的耦合作用, 能带结构更加复杂, 需要识别不同能带对应的元胞运动模式, 从中排除与所关心的运动模式无关的能带曲线, 最终得到“纯净”波动模式的能带特性. 另外, 材料和结构中必然存在一定的阻尼, 在原有模型基础上进一步考虑阻尼的影响可以改善理论模型的预测精度, 更有利于揭示力学超材料中能量损耗机制. 建模中, 通过在弹性模量上添加虚部的方式引入阻尼, 并在应用Bloch 定理时假设频率为复数, 这样除了可以获得不受阻尼影响的色散曲线, 还可以计算每个Bloch 模式的时间衰减, 以此得出阻尼比随波数变化的曲线, 从而确定各个Bloch 模式的损耗因子(Hussein & Frazier 2013). 图30 比较了有无阻尼条件下声子晶体的能带特性, 发现阻尼对高频能带曲线有较大影响, 且在不同波矢量下, 声子晶体具有不同的阻尼比特性, 因此阻尼对波传播方向性也具有显著的影响.

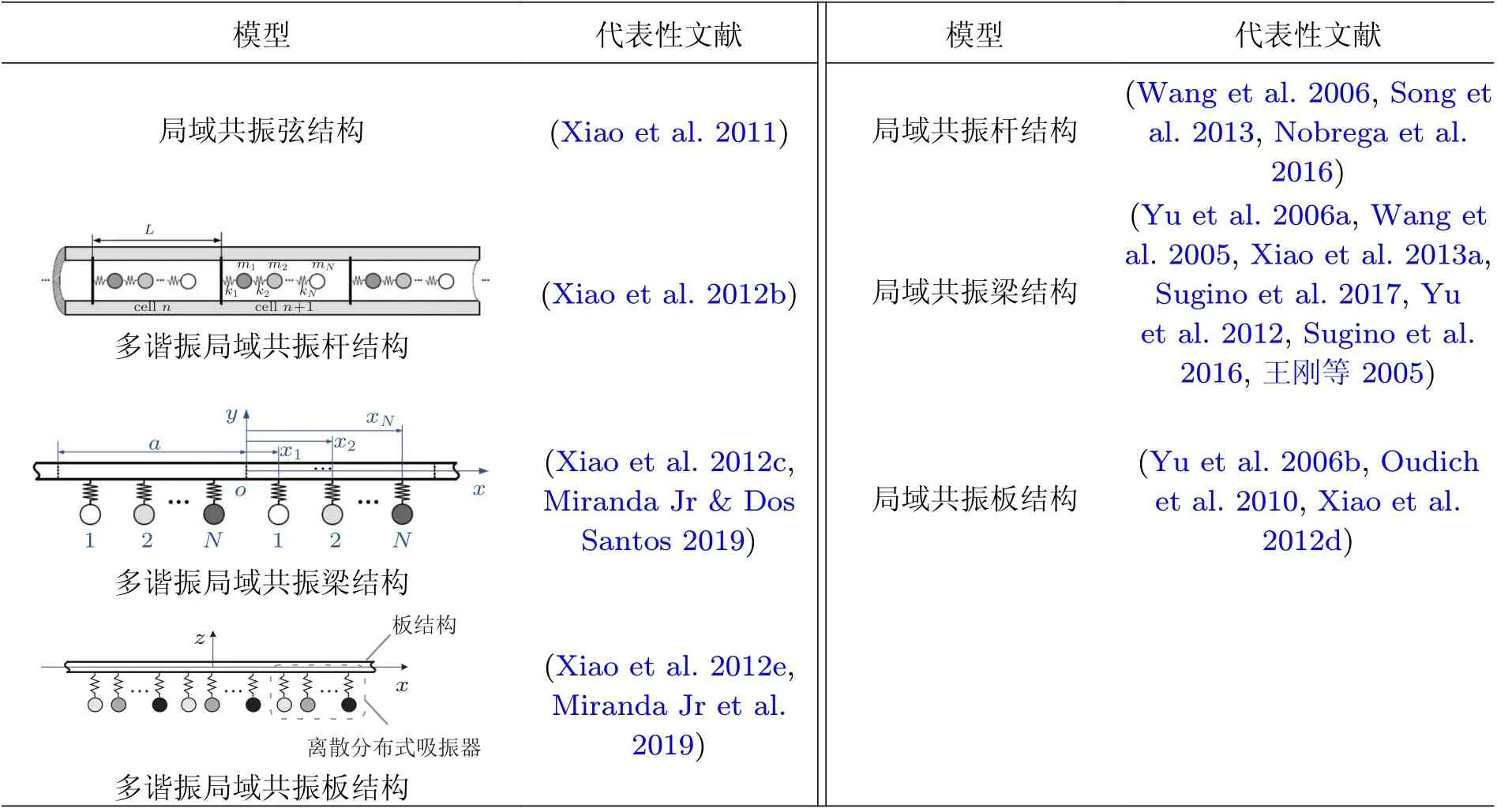
表1 梁、板类力学超材料带隙计算理论模型

围绕带隙的展宽问题, 研究者提出了基于多谐振效应和带隙耦合的解决思路. 首先, 通过在结构胞元中引入并联型多阵列局域共振单元或串联型多自由度局域共振单元 (如表1 所列) , 实现结构胞元中局域共振单元的多频谐振作用, 在不增加附加质量比的条件下, 扩宽了带隙作用频段(Xiao et al. 2012b). 另外, 局域共振超材料中的局域共振和布拉格带隙存在相互耦合、相互转化的现象. 图31 为梁类局域共振超材料中两种带隙的调控规律, 发现经合理调节参数, 可使两种带隙精确或近似耦合成为超宽带隙; 当两种带隙被调节至相互靠近时, 不仅局域共振作用对Bragg 带隙可以产生展宽效应, 而且周期晶格的Bragg 散射作用对局域共振带隙也可以产生展宽效应(Xiao et al. 2012d, 2013a). 图32 所示为具有多频谐振及带隙耦合效应的超材料梁结构的带隙/减振特性与传统超材料结构的对比, 可以看出, 在附加局域共振子总质量相同条件下,改进的超材料梁结构显著拓宽了结构的带隙及减振频带.

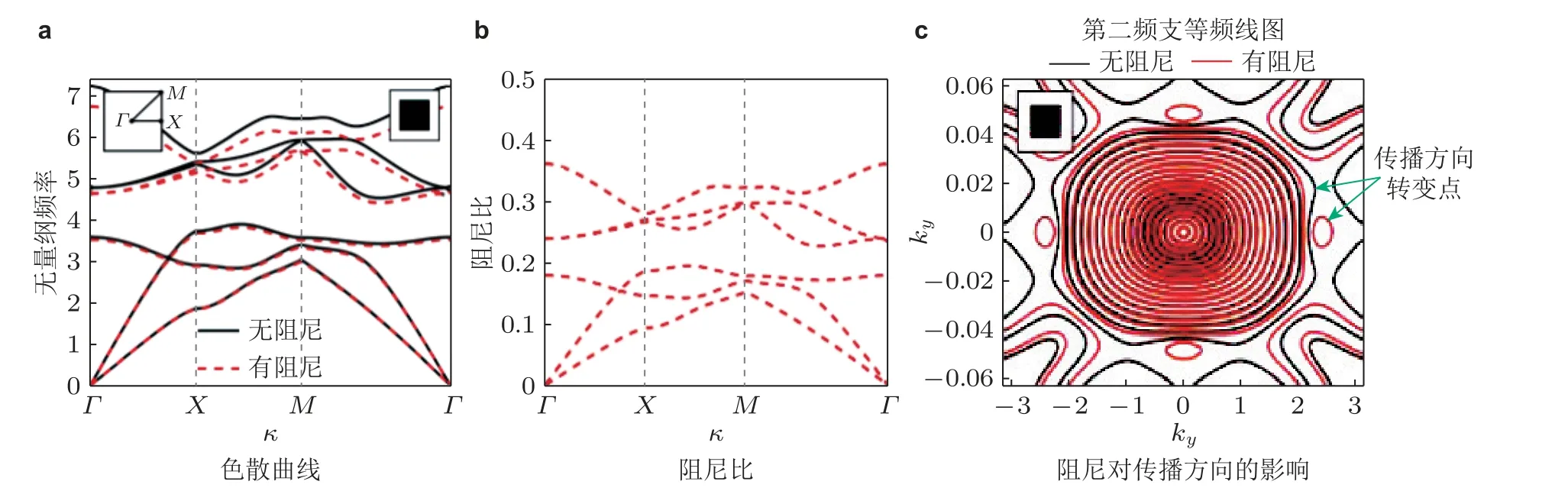
图30阻尼对声子晶体色散特性的影响(Hussein et al. 2014)

面向力学超材料带隙减振的工程应用, 国防科大肖勇等研究了板结构(Xiao & Wen 2020)、梁结构(Xiao et al. 2021b)局域共振力学超材料的带隙频率范围的快速理论预报方法. Sugino等(2017)基于模态分析方法, 得到了一维、二维有限尺度超材料局域共振带隙范围的闭合解析表达式, 并发现对于有限结构, 存在最优附加共振单元数使得其带隙频率范围大于无限结构带隙范围, 且这一最优单元数随着目标频率和附加质量比的升高而增加. 这些工作为力学超材料带隙精确、快速设计提供了支撑.

5.1.2 微结构单元设计

传统局域共振力学超材料中共振单元的结构主要采取“软材料+质量”的形式. 这类力学超材料要实现低频控制往往需要较大的附加质量, 限制了其工程应用. 通过共振单元结构的创新设计, 实现更加低频、高效的振动能量调控成为力学超材料研究的重要方向之一. 本质上讲, 单元设计的目标主要是增大局域共振单元的等效质量、降低等效刚度或是增大等效阻尼作用. 本文重点介绍几类受到广泛关注的微结构单元设计思想.

Xiao 等(2013b)基于悬臂梁式动力吸振器的基本构型, 设计了梁片式局域共振单元, 其结构如图33(a)所示. 仅考虑悬臂梁式吸振器的第一阶振动模态 (二阶以上模态频率通常落在关心频率范围以外) , 那么这种连续参数型的悬臂梁式结构就可以等效为一个集中参数型的“质量-弹簧-质量”系统, 如图33(b)所示, 研究者建立了共振单元等效参数的计算方法, 进而基于该单元构建了局域共振梁结构并验证了其带隙特性 (图33(c)和(d)) . 由于悬臂梁结构具有灵活的可调谐性, 通过参数设计, 可以使超材料中的布拉格和局域共振带隙的宽度都达到最优状态, 而且可以将两个带隙足够接近从而形成一个精确耦合的超宽带隙, 或者是一个近似耦合的超宽“伪带隙”. 此外, 通过设计如图33(e)所示的组合式多自由度共振单元, 还可以进一步实现局域共振带隙的多谐振展宽. 研究发现, 这类悬臂梁式局域共振力学超材料可以在同等附加质量下实现更宽带低频的振动抑制效果, 为力学超材料的轻质减振设计提供了一种有效的方案 (图33(f)和(g)) .

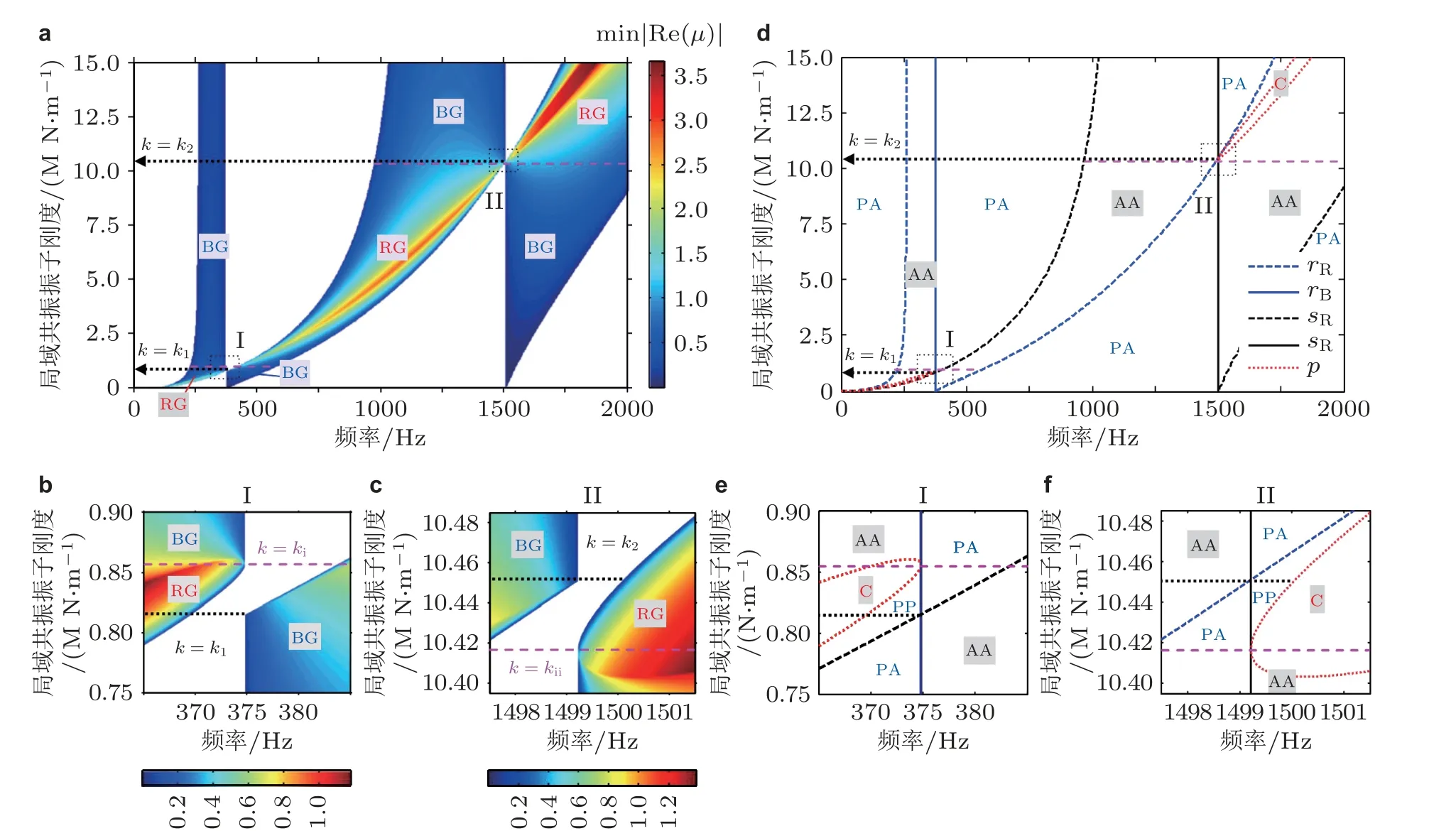
图31力学超材料梁中局域共振子参数对两种带隙的协同调控规律. (a)～(c)理论计算得到的两种带隙演变规律, BG 代表布拉格带隙, RG 代表局域共振带隙; (d)～(f)基于带边频率解析公式预报的带隙范围演变规律. k = k1, k2: 两种带隙相互耦合条件; k = kI, kII: 两种带隙相互转化条件

图32传统单频谐振超材料梁结构和具有多频谐振及带隙耦合效应超材料梁结构的带隙与减振特性对比. (a)带隙衰减特性对比 (η 代表附加局域共振子阻尼因子) , (b)减振特性对比. 注: 相比较的超材料梁具有相同的基体梁结构, 且附加局域共振子的总质量相同

图33梁片式局域共振力学超材料及其振动特性

Yimaz 等(2007)设计了一类基于线性位移放大机构的单元, 可以使其动态等效质量大于实际质量, 实现惯性放大的效果, 从而在不增加质量下得到更低频的带隙. 这一思想首先在一维弹簧质量离散系统得到验证, 进而扩展至其他集中质量系统(Orta & Yilmaz 2019, Yuksel & Yilmaz 2020)(如图34(a)所示). 通过分析这类惯性放大力学超材料的模态能量分布特性和有限结构振动传播与衰减特性, 发现其频响函数中带隙频率范围内会产生与局域共振超材料类似的反共振峰, 但是在模态能量分布上与局域共振有所不同, 主要局域在激励位置附近而非各个共振单元处(Yilmaz & Hulbert 2010). 在连续系统中, 惯性放大单元通常通过铰支杆与质量块构成的机构来实现, 研究者基于此设计了一维(图34(b))、二维(图34(c))惯性放大力学超材料, 得到梁板结构的弯曲振动、扭转振动的低频带隙控制方法(张印等 2016, Muhammad et al. 2020, Yuksel & Yilmaz 2020, Xi C et al. 2021). 近期, 研究者还提出在波纹板、蜂窝板等复合材料上引入质量放大单元, 可以在相对较小的附加质量下实现低频、宽带的振动能量抑制效果. 传统的惯性放大力学超材料仅考虑线性变形, Zhou 等2019)在具有“高静低动”非线性刚度特性的共振单元中引入惯性放大机构, 并基于这一单元设计了超材料梁, 得到比原有超材料更低频的带隙.

图34(a)质量放大力学超材料元胞构型 (Orta & Yilmaz 2019, Yuksel & Yilmaz 2020) ; (b)一维质量放大超材料设 (Muhammad et al. 2020, Orta & Yilmaz 2019); (c)二维质量放大超材料设计 (Xi et al. 2021, Yuksel & Yilmaz 2020, Zhang Y et al. 2016)

声学黑洞是近年来发展起来的一种新型的波动控制技术, 利用薄壁结构几何或材料参数的梯度变化, 使波在结构中的传播速度逐渐减小甚至接近于零, 从而不发生反射并将能量聚集在特定位置. 如图35 所示, 将一维声学黑洞结构厚度设计为满足幂函数, 当弯曲波从均匀材料传播到声学黑洞时, 波速随厚度降低而减小, 波长被压缩, 振动幅值增大, 当黑洞厚度减小至趋近于0 时, 波的累积相位将会达到无穷大, 理论上弯曲波将不会从边缘反射回来, 从而实现了对结构中弯曲波的全吸收. 二维声学黑洞可由一维结构以厚度零点为中心旋转一周得到. 黑洞还具有使弯曲波向其中心偏转的特性. 汇聚在黑洞中心的能量可以利用粘贴在结构上的阻尼材料实现高效的能量消耗. 声学黑洞结构具有丰富的力学特性, 获得广泛关注, 相关研究包括波传播建模与分析、振动能量的阻尼耗散设计、梁板类声学黑洞结构减振设计等, 季宏丽等 (2017), Pelat 等(2020) 进行了详尽的综述.

声学黑洞同样也为力学超材料设计提供了新的元胞结构形式和波调控特性. Tang 和Cheng(2017a)设计了具有周期声学黑洞单元的局域共振梁结构, 考虑到声学黑洞与梁的共形设计会使结构强度大大降低, 进一步提出了内部挖孔式的超材料结构(Tang & Cheng 2017b). 研究发现,孔洞中的支撑结构具有局域共振效应, 在和声学黑洞的耦合作用下, 可以使超材料具有超宽频带隙特性. 他们还进一步将这一设计思想扩展至二维板结构(Tang & Cheng 2019), 同样实现了中低频弯曲波带隙特性. Gao 等(2019)设计了具有V 形折叠梁的声学黑洞超材料, 可以在结构中同时产生弯曲波和纵波的带隙.

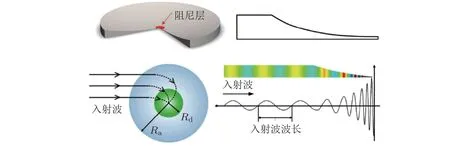
图35一维、二维声学黑洞结构及波传播特性(季宏丽等 2017)

阻尼是材料和结构耗散能量的重要途径, 阻尼减振技术是工程中振动控制的重要手段之一.但是, 天然材料刚度和阻尼存在矛盾, 复合材料能够在一定程度上缓解该矛盾, 但等效模量与阻尼系数的关系仍受界限理论的制约 (如图36(a)所示) , 难以同时实现高刚度、高阻尼性能. 另外, 传统黏弹性阻尼材料低频损耗因子通常较低, 能量耗散能力弱, 在质量、厚度约束下, 难以解决低频振动问题. 因此, 突破高刚度高阻尼和低频能量高效耗散是结构功能材料和振动控制领域关注的热点. Hussein 和Frazier (2013)在研究黏性阻尼局域共振超材料色散关系的基础上, 提出了“超阻尼”的概念, 通过多个局部谐振子和阻尼器的调节, 可实现宽频带的高阻尼比 (如图36(b)所示) , 为高刚度高阻尼材料系统设计提供了新的范例. 力学超材料的超阻尼特性在多种离散晶格系统中得到了验证(Chen et al. 2016b, Bacquet et al. 2018), 在此基础上, 面向连续系统, 通过在材料局部区域引入微结构或局部松散模式, 可以对系统整体刚度和阻尼特性进行设计(Depauw et al. 2018).

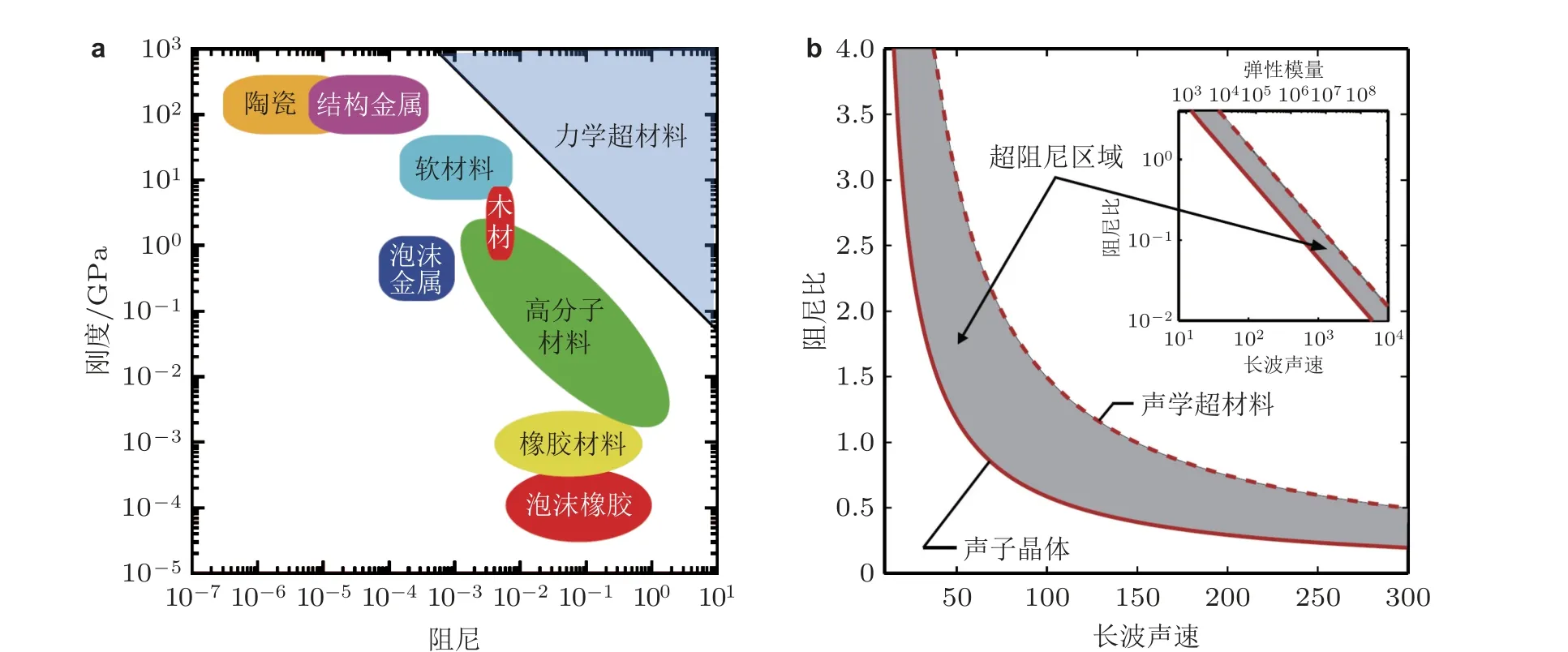
图36(a) 典型材料阻尼与刚度的关系; (b) 力学超材料的超阻尼特性 (Hussein 和Frazier 2013)

5.1.3 带隙减振应用探索

梁板类结构是工程中具有代表性的结构形式, 许多装备如火箭、船舶、飞机等在进行动力学分析时常简化为杆、梁或板结构, 因此其振动问题及控制技术一直得到关注. 近年来, 以加筋结构、蜂窝夹层、点阵夹层为代表的复合梁板结构, 因其轻质、高比刚度/强度等优异特性得到广泛应用. 这类结构在工程上主要采用静态设计-动态校核的方法, 难以实现振动调控特性的定量、精确设计, 导致现代装备振动问题更加突出, 而通过在结构上附加减隔振器件与材料的传统振动控制方法在质量、空间约束下难以有效处理低频宽带振动. 力学超材料的亚波长带隙特性为突破这一问题提供了新的手段. 基于前述力学超材料元胞构型和低频宽带设计方法, 结合工程中典型的梁、板结构的减振设计需求, 研究者也开展了大量探索性工作, 主要的研究思路是: 基于梁板类 (复合) 材料或结构, 通过附加、嵌入等方式集成局域共振、负泊松比、准零刚度等微结构单元构筑力学超材料, 基于带隙机理进行振动调控设计, 实现目标频段内振动的高效衰减或局域作用(赵伟佳等 2020).

Song 等(2019, 2020)以直升机蜂窝夹层壁板结构减振为目标, 通过在其上周期附加由较轻的软材料块和较重的硬材料块构成的局域共振单元, 形成力学超材料复合夹层板结构, 如图37(a)所示. 仿真和实验结果表明, 附加质量为基体板的56.6%时, 能够针对设计频段形成局域共振带隙. 分析表明, 在引入偏心设计后, 附加结构对基体板同时产生等效的附加质量和附加转动惯量的作用, 形成宽频的弹性波带隙, 能够显著改善板结构对振动的抑制效果. Szefi (2003)结合直升机主减速器隔振这一背景, 针对一维周期层状声子晶体结构, 进行了禁带频段设计研究, 并进一步通过引入质量放大单元、压电主动控制设计等手段, 使对振动的有效抑制范围向低频拓展.

针对航天器平台微振动问题, Chen 等(2013)在梁结构基体上周期性地贴附轻质压电分流单元, 利用分流电路的谐振效应替代弹簧-质量谐振系统, 设计了如图37(b)所示的半主动型超材料梁结构, 振动测试结果表明通过一定的控制电路, 力学超材料结构的局域共振频率、等效参数等可以便捷地进行主动调节, 显著的提高了弹性波控制带宽和设计的灵活性, 极大的拓展和增强了亚波长结构对弹性波/声波的操控能力. Wen 等(2016)进一步将这一思想扩展至板结构的振动传播控制, 深入研究了其方向带隙特性, 为压电分流型力学超材料的振动调控应用提供了设计方法.

对于工程中广泛应用的轻质夹层结构, 由于夹芯层单元本身具有周期排列特性, 因此通过芯层材料参数和结构参数的设计, 可以在结构中获得弹性波带隙, 并将这一特性用于振动抑制.(Ruzzene et al. 2002, Ruzzene & Scarpa 2003). Chen 等(2017b)进一步设计了具有周期附加振子与周期芯层的夹层梁结构, 发现这种集成设计可以进一步拓宽振动控制的带宽. 类似的, 研究者将局域共振子微结构附加到点阵桁架夹层结构的每一个周期单元, 设计了点阵桁架夹层力学超材料结构(Guo et al. 2021, Zhang et al. 2021a, Li et al. 2021b). 数值仿真和实验测试结果均表明,这类点阵桁架超材料结构能实现显著的低频振动抑制 (如图37(c) 所示) . 轻质夹层结构自身具有较好的静力学性能, 将力学超材料引入轻质夹层结构, 有望推动静动一体化多功能力学超材料的发展(Yuan et al. 2021).

5.2 非线性力学超材料及其减振机理

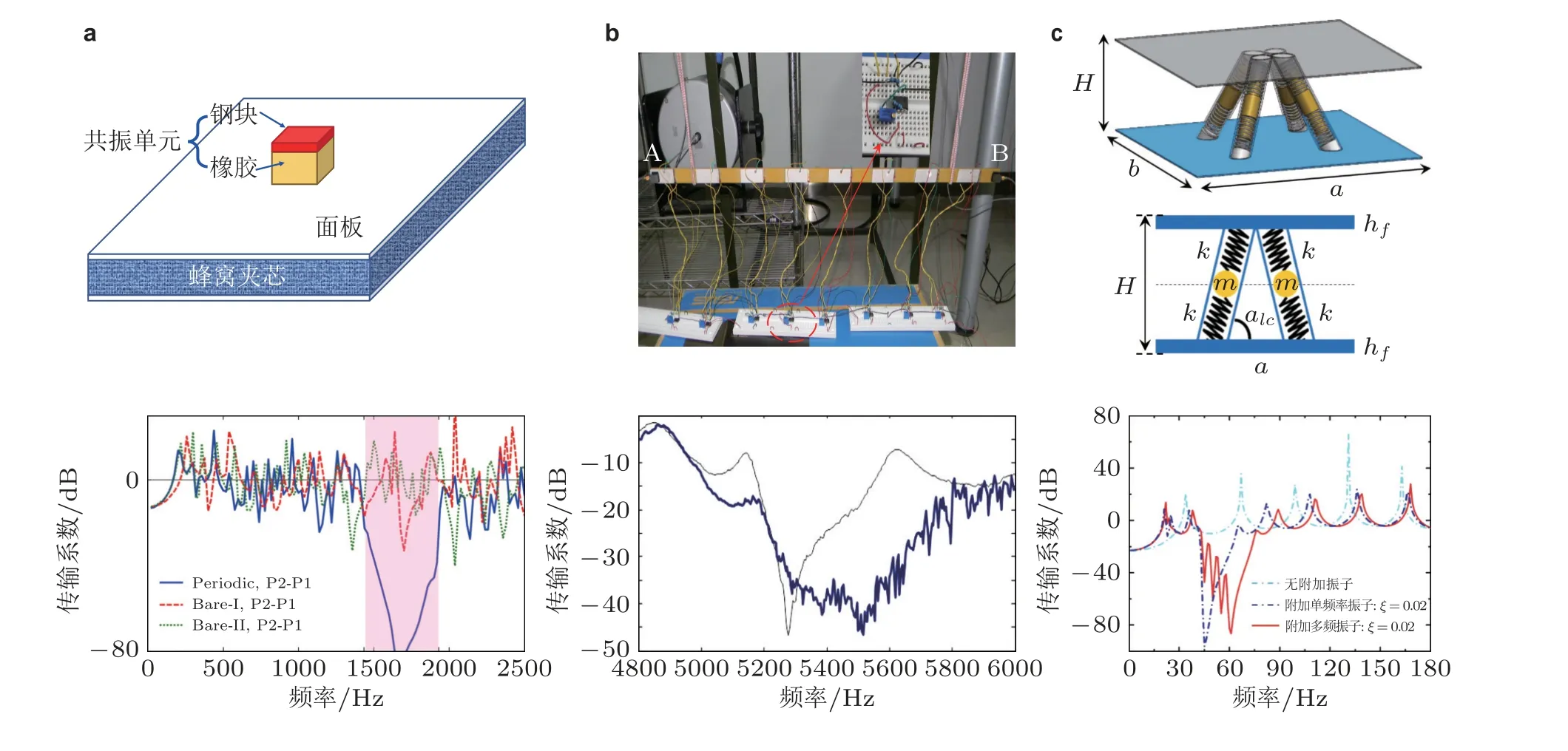
图37力学超材料结构及减振特性. (a) 蜂窝夹层板力学超材料(Song et al. 2019); (b)具有反馈式分流电路的主动超材料(蓝色实线为附加分流电路, 黑色虚线为电路短路) (Chen et al. (2013), (c) 点阵桁架夹层力学超材料(Zhang et al. 2021a)

前文所述力学超材料的研究大多基于对结构的线弹性变形假设而展开, 可以称为线性力学超材料. 非线性力学超材料, 又称非线性弹性/力学超材料, 是指具有非线性动力学特性的力学超材料, 是近年来新兴的研究方向. 非线性超材料通常也是一种周期结构, 其相关工作可追溯至1955 年对非线性离散周期模型 (即FPU 模型) 的研究(Fermi et al. 1955). FPU 模型可以模拟多种物理系统(Gallavotti 2008), 极大推动了热力学、混沌动力学、孤立子理论、非线性声学等非线性物理领域的发展(Cretegny et al. 1998, Ganesh & Gonella 2015). 当前对非线性力学超材料的研究主要包括两类模式: 第一类是研究流体介质中高强声 (＞130 dB) 在线性超材料结构中的传播特性, 其非线性效应来自于高强声对流体的作用, 超材料的结构变形依然为线弹性; 第二类是研究波在非线性超材料中的传播特性, 其非线性效应来自于超材料的微结构变形.

第一类研究可归类为非线性声学的范畴, 通常关注的模型是多孔材料结构、含Helmholtz 共振腔的结构等. 早在1992 年, Sugimoto(1992)就研究了强声下周期性Helmholtz 共振腔的管路中的非线性声场, 利用共振腔来抑制结构中的冲击波; 进而, Richoux 等(2007)研究了管路上周期性Helmholtz 共振腔的非线性对色散带隙截止频率的影响. 对微穿孔板和含Helmholtz 共振腔的力学超材料的研究表明, 在一定程度上提高声压能够提高超材料的最大吸声系数(Tayong et al.2010, Achilleos et al. 2016, Zhang et al. 2021b), 在这种超材料波导中还能够传播声孤立波(Junca & Lombard 2020).

第二类研究模式中引入了结构非线性及其与波的耦合, 因此可带来丰富的物理现象. 早期对类似超材料模型的研究对象为颗粒晶体. 颗粒晶体可视为FPU 的实验物理模型, 它是通过Hertz接触率控制非线性耦合的简单离散点阵周期结构, 球体颗粒晶体中“颗粒”的运动控制方程为

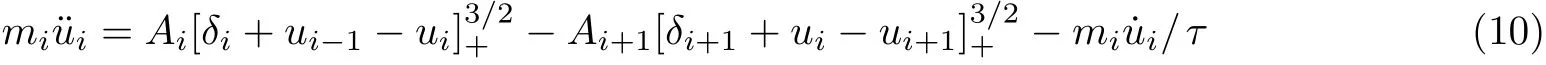
其中, 下标“+”代表括号中的项只可取正, 当为负时值为零 (相互接触无拉力) ,δi为静态载荷F0作用下产生的变形. 1983 年以来, 研究者深入广泛地研究了颗粒晶体中的孤立波、缺陷态、色散、带隙等非线性弹性波动力学特性(Nesterenko 1983, 2001; Geniet & Leon 2002; Daraio et al.2005, 2006, Boechler et al. 2011). 但这些工作中的绝大多数对象都不具备亚波长、负质量密度、负模量等超常特性. 针对工程振动控制应用, 本文重点讨论非线性力学超材料在亚波长波调控方面的研究进展.

5.2.1 非线性力学超材料的带隙特性

理解非线性力学超材料带隙的内涵是本领域最基本的问题. 这里, 以如图38(a)所示的非线性局域共振结构为例来说明. 基体m0与局域共振质量mr之间的连接刚度由典型的立方非线性刚度kru+knu3描述, 其中kr和kn分别为线性和非线性刚度系数, 本文设kn＞ 0. 由图38(b)可知,非线性共振曲线向右弯曲且产生分岔, 这一看似平常的非线性现象将从本质上改变非线性超材料的特性. 根据运动方程, 可以求解出该共振单元的近似等效质量meff为

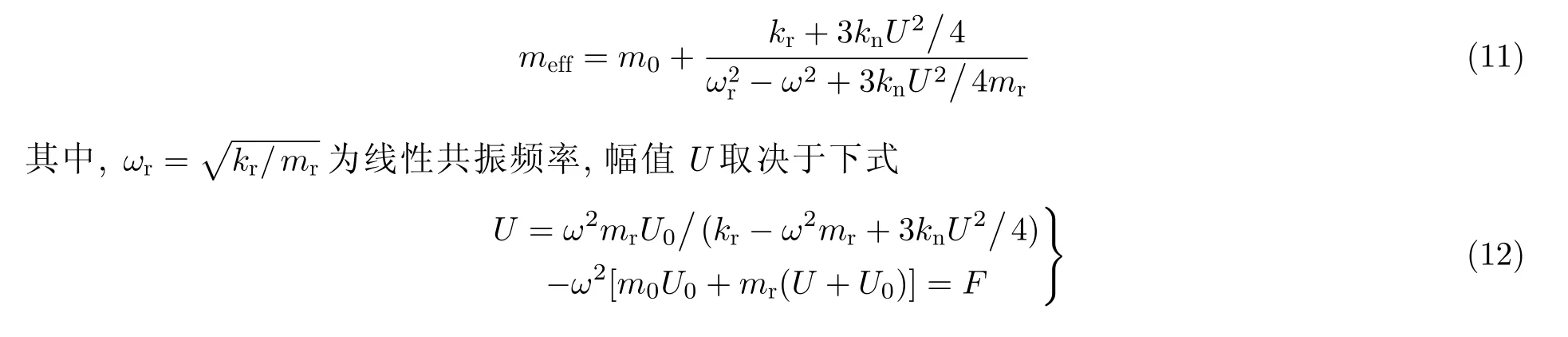
其中F为基体m0上的作用力,U0为m0的位移. 由此可见, 非线性超材料的等效质量密度特性取决于输入幅值U0和F(或者波的振幅) , 增大幅值将使负质量密度区产生偏移, 且求解时给定F和给定U0将得到不同的现象. 由于meff依赖于幅值, 则其他依赖于质量密度的特性, 如波速、波矢、带隙等色散特性都将与幅值紧密相关, 可通过调控幅值达到进一步拓宽设计域的目的. 典型的局域共振带隙如图38(c)所示, 非线性使带隙向高频偏移(Fang et al. 2016). 在幅值变化的情况下, 带隙边缘的波传播特性将产生奇异的状态变化, 如图38(d)所示, 当幅值小于临界值Ac时, 该频率的波处于被抑制的状态; 但是状态在Ac产生突变, 继续增大幅值将使该频率的波突变到可传播状态, 从而产生了带隙的双稳态特性. 实验中, 当幅值从较大的值逐步降低时, 传递特性曲线将产生滞回环. 若带隙具有多个稳态, 大幅值时的滞回环形状将变得复杂.

对非线性带隙特性的研究十分广泛(Jiao & Gonella 2019, Bae & Oh 2020), 这类研究中通常直接应用Bloch 定理确定的周期边界, 分析思路与线性超材料相同. 然而, Bloch 定理的线性理论本质并不适用于非线性周期介质的波动特性分析中. 最近, Fang 等(2020)通过解析、理论与实验研究了含桥连耦合增强非线性局域共振单元的超材料结构, 对于相同长度的结构, 极强非线性产生的传递衰减范围远大于线性超材料的带隙范围 (图39(a)) , 原因在于: 近场的弹性波衰减发生在非线性影响的偏移带隙内, 随着传播距离的增大, 其衰减范围不断变宽, 最终在远场产生一个超低频超宽带的带隙 (图39(b)) . 这是一个无任何外部干预的自适应过程, 即使在无阻尼条件下也可以发生, 带隙的自适应变宽称为自扩展. 自扩展带隙说明强非线性条件下的能带结构随着传播的空间/时间自适应变化, 这与Bloch 定理时空不变性的内涵存在本质差异. 自扩展的低频宽带衰减来自于带隙效应在不同空间位置上的累积. 自适应能带结构和自适应波传播为强非线性超材料中能带和波动特性分析提供了一个更完整的框架.

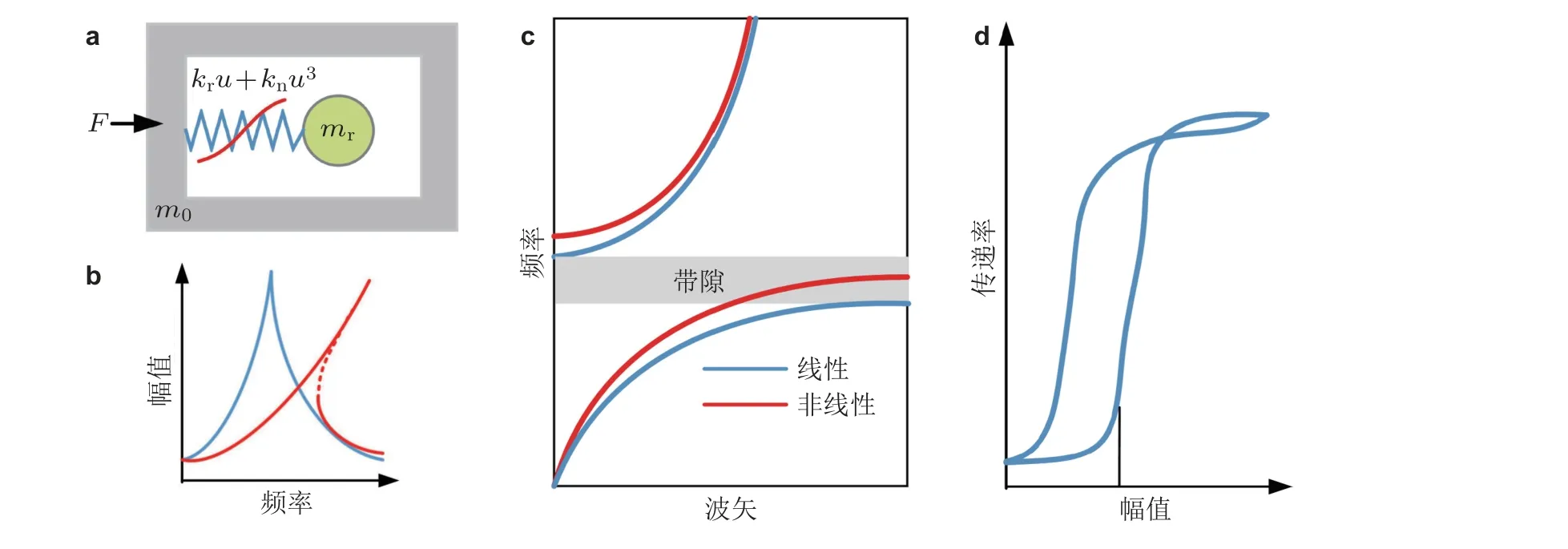
图38非线性力学超材料的带隙特性. (a) 非线性局域共振结构, (b) 典型非线性共振曲线, (c) 典型局域共振带隙, (d) 带隙边缘波传播特性

5.2.2 混沌响应与超低频超宽带振动抑制特性

强非线性力学超材料中可以产生混沌效应. 混沌是相比高次谐波更为复杂的情形, 其对有限大非线性力学超材料结构的振动响应具有显著影响. 如图40 所示, 以双原子链模型为例, 有限大线性超材料结构的带隙能有效抑制结构振动, 通带由密集的共振峰组成, 共振峰的数量等于结构自由度. 然而, 随着非线性强度的增大, 局域共振带隙区间产生偏移, 且高于带隙范围内的通带内的响应也会被显著抑制, 这种效应在无阻尼结构中也存在. 带隙的偏移能够解释部分频带内的衰减, 但无法完全揭示整个频带内的共振抑制效应. 通过大量的分岔、吸引子和频谱分析表明, 通带内非线性共振频带的响应在一定的幅值下变为混沌的, 混沌响应使共振得到显著抑制(Fang et al. 2017a). 因此, 振动变为混沌的通带定义为混沌带 (或者称为非线性共振频带) , 混沌带将振动抑制从带隙拓展到通带, 为振动抑制开辟了新途径. 进而, Fang 等(2017b) 提出了如图41所示的一维和二维强非线性力学超材料结构, 证明这种机理能产生超低频超宽带的振动抑制效果. 非线性局域共振带隙的桥连耦合可以高效调控混沌带带宽和作用效率(Fang et al. 2018a).系统的参数分析表明, 这种低频宽带的振动抑制效果对附加质量不敏感, 因此可以用小附加质量实现宽低频振动控制(Fang et al. 2016, Sheng et al. 2021).

最近, 由非线性产生的拓展振动抑制带宽的效果也在压电超材料中得到验证(Zhang et al.2021c). 通过组合强非线性和线性超材料还能同时获得窄带高效的带隙和宽带的混沌带, 提高整体抑制效果(Yu et al. 2021a).

强非线性力学超材料中还会产生高次谐波(Fang et al. 2018b), 典型的为二次谐波和三次谐波(Zhang J et al. 2016). 高次谐波的特性取决于非线性局域共振的分岔与跳变, 与质量密度和带隙存在同步变化特性, 但高次谐波可能会产生奇异的峰值. 高次谐波使弹性波波形畸变, 其与基波的耦合特性也会随着传播距离变化. 此外, 将强非线性力学超材料与线性力学超材料结合还可设计出小尺寸、亚波长的双向二极管(Fang et al. 2021), 使非线性超材料具有更加丰富的波调控功能.

图39强非线性力学超材料中的自适传播特性. (a) L 和N 分别代表线性和非线性超材料的传递率, (b)整个频带上波的传递率随传播距离n 的变化规律

图40双原子非线性力学超材料模型的特性

5.2.3 多稳态力学超材料

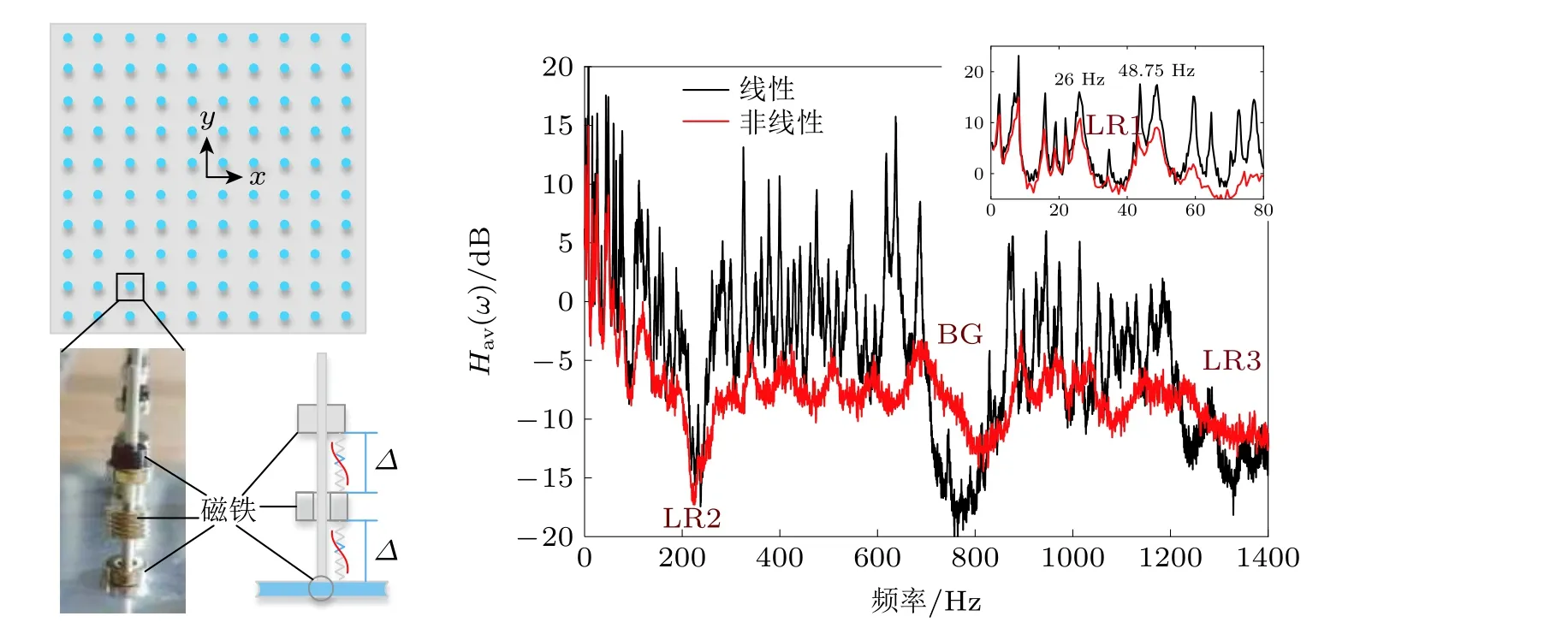
图41超低频超宽带的强非线性力学超材料结构及其振动传递率

对于典型的非线性Duffing 振子, 如其线性刚度部分为负, 则该振子具有两个静态稳定平衡点, 称为双稳态振子. 负刚度的存在使由双稳态振子构成的周期结构产生新颖特性, 典型结构如图42 所示. 单个负刚度振子存在两个稳态, 由其构成的周期链实际上具有非常多的稳定状态.这种结构中双稳态振子的负刚度使波传播存在两种机制(Nadkarni et al. 2014): 当幅值较小时是具有色散特性的线性弹性波; 当幅值较大时可传播孤立波. 改变振子的负刚度可大范围调控周期结构的带隙特性(Bernard et al. 2014, Meaud & Che 2017). 大多数对多稳态周期性力学超材料的研究都认为每个稳态单元在不同稳态间的跳变是依次发生的, 但是大量的仿真研究表明, 当稳态谐波和冲击波在无限长双稳态周期结构中传播时双稳态周期结构中双稳态振子的突弹跳变顺序呈现出一般规律性和局部随机性. 大部分的波能量在很长一段时间内被储存在跳变振子中, 这表明了一种奇异的能量传输现象, 即能量局部化. 当幅值增大或压缩变形量增加到临界值时, 其带隙的起始频率可向前迁移到约0 Hz, 这就提供了动态可调性. 因此, 双稳态周期结构具有低频和宽带的衰减特性, 而可调谐的衰减波段取决于振幅. 对于冲击波的传播, 冲击脉冲的幅值、宽度和系统阻尼对波传播特性可以产生显著影响(Liu et al. 2021b).

5.3 机械超材料的减振抗冲设计

将力学超材料的思想拓展至材料静力学性能调控后, 其内涵更加丰富, 特别是先进制造技术的飞速发展, 为实现更丰富多样化的力学超材料构型提供了支撑, 使材料逐渐突破机械性能的极限,催生更新奇的力学效应. 本节重点结合力学超材料超常静力学特性讨论其在工程减振抗冲结构材料及器件设计方面的应用可能. 另外值得注意的一点是, 工程中往往同时关注材料的静态、动态力学特性, 在力学超材料的体系框架下, 同时实现材料静态、动态力学特性的调控是当前研究的一个重点.

5.3.1 负泊松力学超材料

图42由双稳态单元构成的一维链状力学超材料 (Nadkarni et al. 2014)

泊松比ν定义为材料单轴拉伸 (或压缩) 时, 横向应变εy与纵向应变εx之比的负值, 即ν=-εy/εx, 显然, 泊松比与受力方向有关. 自然界中大部分材料在拉伸 (压缩) 作用下, 横向收缩 (伸长) , 因此泊松比总是正的. 当泊松比为负值时, 材料会表现出与反常于一般材料的拉胀特性, 因此又被称为拉胀材料 (auxetic material) (Caddock & Evans 1989, Evans & Caddock 1989). 对于负泊松比材料的研究已经有很长的历史了, 人们首先发现自然界中的活骨组织(Ashman & Rho 1988, Lees et al. 1991)、母牛皮肤组织(Gatt et al. 2015)和一些天然矿物(Keskar & Chelikowsky 1992)等天然材料会表现出拉胀效应, 这是由其微观细胞或分子/原子的特殊结构或序构产生的. 由于材料的弹性力学特性与尺度无关, 负泊松比若能在微观或原子、分子尺度获得,也同样可以在介观到宏观尺度通过微结构设计实现(Alderson 1999). 在自然界负泊松比材料的启发下, 20 世纪80 年代, Lakes (1987)首先提出了一种基于具有泡沫结构的人工负泊松比材料的制备方法, 通过将传统开孔热弹性泡沫材料通过热处理变换为具有凹角微结构的泡沫材料, 实现材料的拉胀特性, 开启了人工负泊松比材料研究的序幕, 这实际上也体现了超材料通过微结构调控宏观力学性能的思想.

通过结构单元设计, 力学超材料的负泊松比数值具有广阔的调控区间, 可以低至-20 (Yu et al. 2018a), 人们也提出了多种实现负泊松比特性的元胞构筑方式, 其中研究最为广泛的元胞形式包括: 内凹蜂窝结构、手性结构和旋转刚体结构 (如图43 所示) . 基于这几类元胞构造的二维、三维力学超材料在受力作用下的形变机理和宏观力学特性在以往文献中有较为全面的综述和总结(Saxena et al. 2016, Kolken & Zadpoor 2017, Ren et al. 2018). 负泊松比力学超材料的一种特殊情况是, 当其横向应变等于纵向应变时, 得到泊松比为-1. 此时, 与五模力学超材料相反, 材料的体积模量K远远小于剪切模量G, 即材料参数接近Milton 图中G轴. 这类力学超材料仅支持易变形模式, 即在外力作用下, 其形状不会发生变化, 而是随着外力的变化发生整体尺寸的缩放,在文献中, 又被称为胀缩材料 (dilational material) 或单模材料 (unimode material) . 胀缩特性可以通过在结构单元设计中引入滑动机构(Milton 1992)、连杆转动机构(Milton 2013, Cabras &Brun 2014)等来实现.

具有负泊松比特性的力学超材料对冲击和振动能量具有优异的耗散特性, 在减振降噪及抗冲防爆等工程领域具有广泛的应用前景, 具体体现在 (1) 负泊松比具有更高的抗剪强度, 当泊松比趋近于1 时, 剪切模量趋于无穷大. (2) 负泊松比材料具备受压时材料向内部聚集, 瞬时密度增大, 因此能够表现出刚度和韧性增强的特性 (如图44 所示) . 材料硬度H可以由杨氏模量和泊松比表达为:H∝[E/(1-ν2)]γ(其中γ 为断裂表面能) . 可见, 如果泊松比接近-1, 材料会变的非常坚硬. (3) 材料接触表面积与 ( 1-ν2)/E成正比, 因此材料具有抗压痕特性, 这与传统材料刚好相反, 使得负泊松比材料具有更好的抗破坏和冲击抵御能力, 当结构受到冲击作用时, 材料向破坏处聚集, 实现填充或减小破坏口的效果, 提高抗冲防爆能力, 保护装备和人员安全. (4) 在弯矩作用下, 由一般材料构成的梁、板结构会呈现出横向曲率与弯曲主曲率相反的反背曲率, 变成呈现马鞍形, 而负泊松比材料则可以实现横向曲率与主曲率一致的同向曲率现象, 变形呈现穹顶形, 可以更好的保护结构, 避免损伤.

图43典型负泊松比力学超材料. (a) 内凹蜂窝结构, (b) 手性结构, (c) 旋转刚体结构(Frenzel et al.2017)

图44负泊松比材料的压痕阻力现象

针对冲击吸能结构的工程设计需求, 研究者围绕负泊松比结构开展了一系列研究, 以揭示其动态力学响应及其能量吸收机理. 在遭受冲击载荷时, 负泊松比结构动态力学响应可以分为三个阶段: 线弹性阶段、平台区、致密化阶段(Imbalzano et al. 2018). 相较于传统蜂窝结构变形模式, 负泊松比蜂窝结构受到面内冲击载荷时, 结构向冲击部位收缩, 冲击部位会出现局部刚度增强的现象, 有效提升结构吸能特性及其防护能力. 另外, 负泊松比蜂窝结构所能承受的冲击应力大于传统蜂窝结构(Hou et al. 2016). 而传统蜂窝结构受到冲击时结构发生整体弹塑性变形, 受冲击区域并未发生局部刚度增强效应, 防护能力有限(Imbalzano et al. 2017, 2018).

以内凹六边形蜂窝结构为例, Jin 等(2016)建立了如图45(a)所示梯度厚度的内凹蜂窝夹芯板模型, 研究其在不同爆炸载荷下变形机理和吸能特性, 并探讨了不同布置方式下夹层板结构防护能力. 结果表明, 壁厚较大时, 内凹蜂窝结构在爆炸载荷下具有较高的平台应力值, 吸能特性良好且蜂窝结构在纵向方向的抗变形能力高于横向方向的抗变形能力. 另外, 与均质内凹蜂窝相比, 具有密度梯度递减的内凹蜂窝结构其抗爆防冲特性最佳. 与常规纵向排列的蜂窝相比, 交叉排列的梯度蜂窝夹芯层 (图45(b)) 可以显著提高结构吸能特性, 增强结构防护能力.

图45(a) 内凹蜂窝夹芯板结构, (b)交叉排列内凹蜂窝夹芯板结构(Jin et al. 2016)

对于内凹蜂窝结构而言, 掌握其在不同冲击载荷下的变形机理及其动态力学响应规律对于设计抗爆防冲结构具有重要意义. Dong 等(2019) 通过实验分析及有限元模型研究了不同壁厚的内凹蜂窝在准静态载荷下的变形机理及负泊松比效应对抗压强度和吸能特性的影响. 结果表明,厚壁蜂窝与薄壁蜂窝具有不同的变形模式. 如图46(a) 所示, 当厚壁内凹蜂窝结构收到冲击载荷时, 局部发生断裂并压缩, 同时, 左右边界向中心压缩, 根据不同冲击速度产生三种变形模式, 即垂直V、Y 和X 变形模式; 薄壁内凹蜂窝受到冲击载荷时, 表现出局部的收缩与膨胀, 产生水平双V 和Z 变形模式, 如图46(b)所示. 另外, 研究发现, 在压缩过程中, 厚壁内凹蜂窝的弹塑性应变及断裂对能量吸收贡献较小, 而在薄壁内凹蜂窝结构中其弹性应变能占总吸能较大比例. 在此基础上, 为了进一步提升内凹蜂窝的吸能特性, Zhang 等(2020) 将内凹壁用圆弧替代, 提出了如图47(a)所示的仿生内凹蜂窝结构, 并基于一维应力波传播理论及能量吸收效率公式, 推导了仿生内凹蜂窝的平台应力经验公式. 研究发现, 结构元胞拓扑发生变化, 其受到冲击载荷时的变形机理也发生了根本的变化. 根据冲击速度的不同, 仿生内凹蜂窝的变形模式可以分为三种: 均质变形, 跃迁变形和渐近变形. 相较于传统内凹六边形蜂窝, 圆弧蜂窝所能承受的应力峰值较低,但具有更好的能量吸收效率以及受冲击时应力波波动较小, 稳定性更强.

图46(a) 厚壁内凹蜂窝垂直V, Y 和X 变形模式; (b)薄壁内凹蜂窝水平双V 和Z 变形模式(Dong et al.2019)

除了典型的内凹六边形蜂窝结构, 双箭头、星型等负泊松比蜂窝结构也被应用于防护结构设计中. Zhao 等(2018b) 针对双箭头负泊松比结构, 通过仿真模拟推导了临界冲击速度经验公式, 用以区分结构在X 方向和Y 方向上的变形模式. 另外, 提出了一种建立动态抗压强度的理论模型方法, 并通过数值计算方法验证了该模型的准确性. Chen 等(2021)讨论了双箭头负泊松比结构几何参数对结构变形机理及吸能特性的影响, 并重点研究了采用导管集中载荷时结构变形及面板脱落情况对吸能特性影响规律.

Yang 和Ma (2021)通过理论分析、数值模拟和实验方法, 研究了应变硬化、冲击速度和初始负泊松比及梯度壁厚对三维双U 型负泊松比结构动态力学行为的影响 (见图47(b)) . Lu 等(2021)采用双斜壁代替了星型蜂窝的水平壁并引入与星状蜂窝四个内凹角接触的薄壁圆, 设计了新型负泊松比蜂窝, 如图47(c)所示, 研究发现, 该结构在不同的冲击速度下有不同的变形模式, 其应力-应变曲线存在两个平台应力阶段, 这种多阶平台特性更有利于对爆炸冲击能量的吸收.

随着负泊松比材料逐渐走向工程应用, 人们对这类结构的关注逐渐也从单纯的静力学设计拓展到动态波调控特性, 负泊松比力学超材料本身是一种人工周期结构, 因此对于负泊松比结构动力学特性的研究也沿着从人工周期结构到力学超材料的发展脉络推进, 其中重点关注在保持结构静力学特性的条件下如何实现对动态波动能量的调控. 基于这样的思路, 佐治亚理工学院Ruzzene 团队在负泊松比力学超材料方面的工作具有一定的代表性. 他们首先从力学承载角度入手, 提出将手性蜂窝结构嵌入飞机翼型轮廓内, 以使其具有弦向弯曲柔度, 并具有承受扭转载荷的能力(Spadoni & Ruzzene 2007). 进而, 研究了具有手性和内六角元胞的负泊松比力学超材料的动力学特性(Gonella & Ruzzene 2008, Spadoni et al. 2009), 通过分析其能带特性, 提出其带隙特性可以用于结构振动的隔离控制. 进一步结合局域共振力学超材料思想, 通过在负泊松比基本结构中嵌入局域共振芯体, 可以实现材料的高刚度高阻尼特性, 并探索了振动控制中的应用(Ruzzene & Scarpa 2003, Baravelli & Ruzzene 2013). 研究者通过深入分析这类嵌入芯体的负泊松力学超材料的带隙特性和优化设计方法, 可以进一步提升其低频宽带的振动抑制特性(Liu et al. 2011b, Qi et al. 2019).

5.3.2 负刚度力学超材料

负刚度力学超材料与前面介绍的各类力学超材料相比, 表现出完全不同的反常力学行为. 这是因为它打破了材料弹性张量正定的假设, 具有不稳定性, 只有受约束下才能保证材料系统的稳定. 这类力学超材料通常具有两个或多个稳定/亚稳定状态, 在稳态跳变转化过程中展现出负模量特性, 同时吸收和消耗大量能量, 且具有可恢复性, 因此在冲击吸能和减振降噪领域有很好的应用潜力.

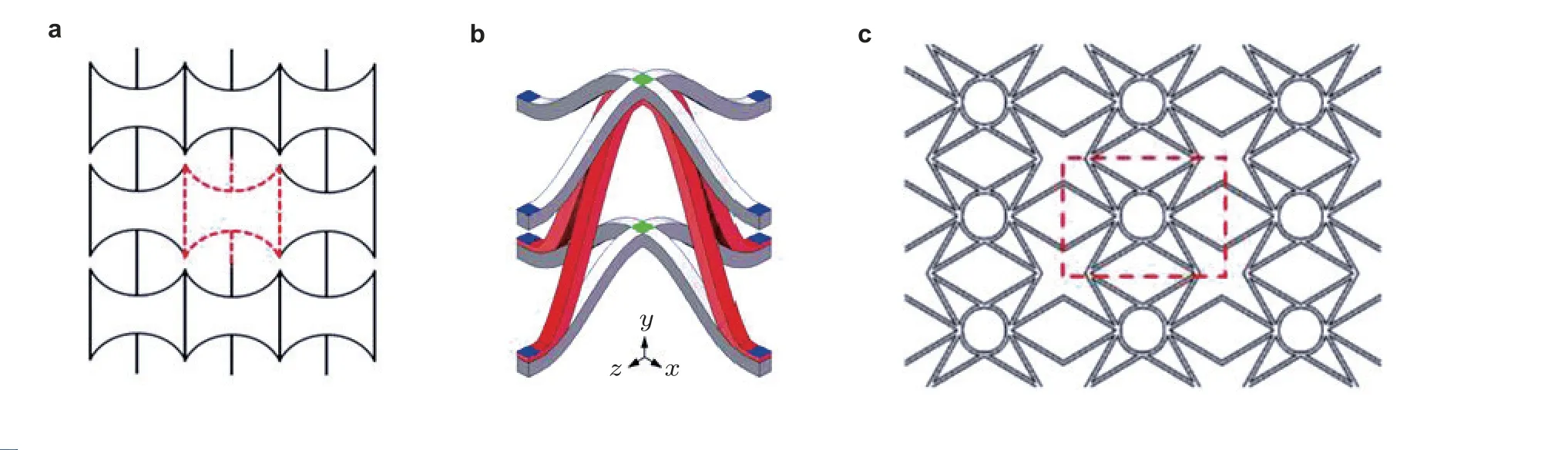
图47新型负泊松比力学超材料. (a)仿生内凹蜂窝结构(Zhang et al. 2020), (b) 三维双U 结构(Yang和Ma 2021), (c)星形负泊松比结构(Lu et al. 2021)

负刚度相对于正常物体的力-位移关系表现出相反的特性, 通常考虑某一特定方向的受力和变形, 因此其本质上是该方向的负模量. 如图48(a)所示, 两端固支的后屈曲梁在受力作用下,随着变形的增加, 单元会产生瞬间失稳现象, 跳变至另一种稳定状态. 状态(1)和(3)表示梁的双稳态, 而状态(2)是不稳定的平衡态, 此时内部存储有能量, 在任意横向微小扰动作用下, 能量迅速释放使结构转变至两种稳态之一. 在这一过程中, 其力-位移关系 (图48(b)) 是非线性的, 具有负刚度特性, 导致结构对扰动的敏感性和不稳定性(Klatt & Haberman 2013). 如图48(c)和(d)所示, 具有双稳态或弹性突跳 (snap through) 特性的结构都会展现出负刚度的特性, 并且具有无摩擦、响应快、低能耗、保持稳态过程中不需要消耗功耗的特点, 因此是一种良好的吸能结构. 基于负刚度结构设计的缓冲器等抗冲防护装备具有良好的吸能特性和完全恢复性(Correa et al. 2015). 将负刚度与正刚度结构并联, 可以实现“高静低动”的准零刚度(Carrella et al.2007)、极端阻尼效应(Lakes 2001b, Antoniadis et al. 2015), 被用于减隔振器件设计, 对低频振动能量具有高效隔离和耗散作用, 可以弥补传统减隔振器低频性能不足的缺陷(Li et al. 2020).

以负刚度结构为元胞构筑的力学超材料兼具“高静低动”的刚度特性和超材料的带隙特性,进一步扩展了材料对振动能量的调控和抑制性能, 具有良好的工程应用前景. Fan 等(2020)设计了由准零刚度单元周期排列构成的力学超材料, 如图49(a)所示, 发现结构在宏观上也能表现出准零刚度的特性, 并且具有良好的隔振特性. Cai 等(2020)设计了由正刚度弯曲梁和负刚度折叠梁组合而成的结构单元构建的一维力学超材料, 通过正负刚度并联实现准零刚度特性, 且单元具有局域共振特性, 从而可以实现低频带隙. 研究发现, 带隙频率可以通过改变材料预应力进行调控, 其本质是对共振单元等效刚度的调节, 此外, 系统中的阻尼可以进一步扩大带隙范围, 但会减少带隙内的波衰减. 由于负刚度力学超材料在动态上具有非线性特性, 因此也可以划归到非线性超材料的研究范畴, 非线性特性使负刚度力学超材料的动态行为变得更加复杂, 波传播和衰减特性与激励的大小相关(Zhou et al. 2019). 值得注意的是, 许多具有负刚度特性的材料同时也具有负泊松比特性(Hewage et al. 2016, 任晨辉和杨德庆 2020), 二者集成设计可以将材料力学性能拓展至Milton 图第三象限, 针对其丰富力学特性的研究还刚刚起步.

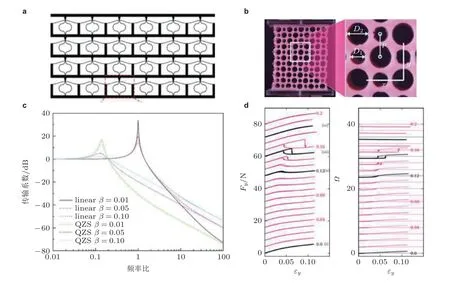
图49(a) 准零刚度力学超材料及其隔振特性 (Fan et al. 2020), (b) 二维多孔软材料及其力学特性(Florijn et al. 2014)

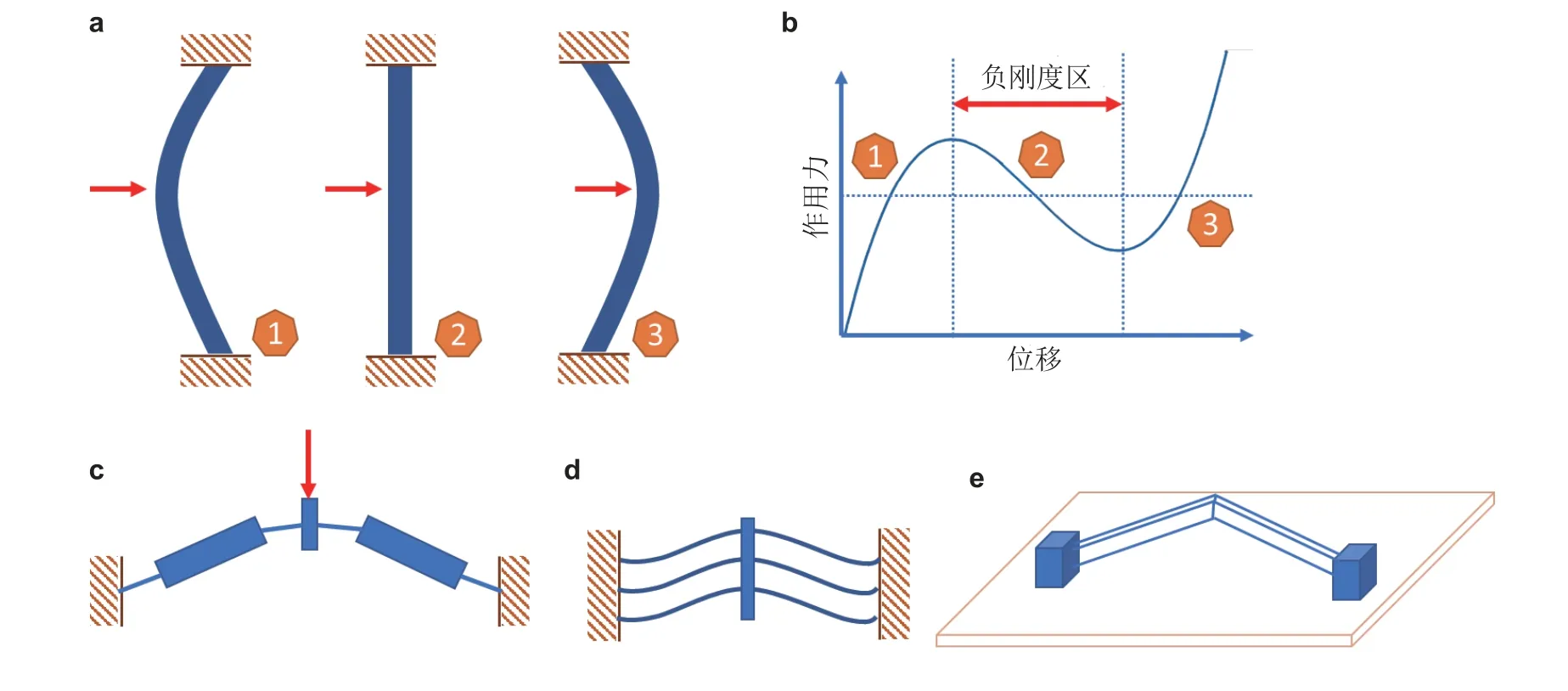
图48(a)梁屈曲变形过程, (b)受力-位移曲线, (c) 机构诱导的全挠性双稳态结构, (d) 预压梁双稳态结构, (e) V 形梁双稳态结构

二维多孔软材料是另一种具有负参数特性的力学超材料. 如图49(a)所示, 具有多尺度周期穿孔的软材料在外载荷作用下, 利用弹性材料的屈曲不稳定性, 具有从一种亚稳定状态跳变至另一种或几种亚稳定状态的特性(Florijn et al. 2014). 这类材料可以实现在不同的稳定状态下使材料具有不同的、可调控的杨氏模量, 但在模式转换过程中, 材料瞬时也可以展现出负刚度特性(Bertoldi & Boyce 2008, Overvelde et al. 2012, Shan et al. 2015) , 具有对冲击激励有良好的吸收特性.

6 其他新颖力学超材料

6.1 可编程及智能力学超材料

灵活的可设计性是力学超材料获得关注的最主要原因之一, 在力学超材料研究初期, 这种可设计性主要体现在对各种超常力学性能的实现, 随着研究的不断深入, 近年来, 具有力学特性可编程、可实时调控, 甚至可以根据外界环境 (边界条件、载荷条件) 变化而自主做出不同响应的力学超材料成为领域内关注的新热点, 将材料力学性能的设计向时间和空间维度扩展, 使其具有更好的环境适应性, 为力学超材料提供了更为广阔的应用空间和场景.

力学超材料的可编程设计的基本思路是: 根据外界环境变化和材料性能设计需求, 改变元胞拓扑构型或力学参数, 从而实现宏观力学性能的时空调控. 可编程特性可以通过无源被动或有源半主动的方式实现.

在完全被动无源的条件下, 实现力学超材料在空间和时间维度上的可编程、可调控主要包括两种方式, 一是通过不同类型元胞的组合或者同一类型元胞的渐变/梯度设计, 实现力学性能空间分布的可编程. Coulais 等(2016)通过将具有不同形变模式的元胞在空间上进行组合, 构建了10 × 10 × 10 元胞的力学超材料, 使材料受到轴向压缩时, 在不同空间位置上实现不同的、可设计的响应特性. 加州理工大学Daraio 团队构建了基于同一种基材, 但具有不同弹性参数的超材料元胞库, 并可以根据实际结构对材料力学参数空间分布的需求, 选取库中不同的元胞进行优化组合, 最终通过3D 打印技术制备宏观结构(Schumacher et al. 2015). 这些方法都可以认为是基于数据驱动的设计方法. 另外一种完全不同的思路是通过材料在外应力变化时发生模式转化或形状跳变实现材料力学特性的调控. 如Florijn 等(2014)设计了具有双周期特性的多孔二维软材料, 当材料在特定约束条件下受到外载荷作用时, 具有从一种稳定极化模式转换到另一种极化模式的特性. 在这两种不同的极化模式下, 由于超材料的元胞构型发生了变化, 因此材料具有不同的宏观力学特性, 并表现出非线性的单调、非单调和滞后力学特性. 值得注意的是, 对于这类具有多稳态特性的力学超材料, 研究者还非常关注材料在模式跳变的瞬间产生的特殊力学特性,比如负刚度(Rafsanjani et al. 2015)、应变能俘获(Shan et al. 2015)等, 这些特性可以应用于冲击能量吸收从而保护结构.

近年来, 折纸/剪纸力学超材料的发展为实现以上两类可编程超材料提供了一种新的构筑方法. 折纸是由二维材料通过折叠构造三维结构的一种方法, 而剪纸通过在二维材料上进行切口引入额外自由度, 使折纸后构建的三维结构具有更加广阔的性能设计范围(Xu et al. 2017). 这类结构具有典型的可展开性和多稳态特性, 以往研究工作主要从运动学、机构学的角度出发, 探索其在航天器太阳翼、天线等展开结构、机器人/执行机构、柔性电子器件等方面的工程应用(夏进军等 2021). 随着研究的深入, 其静力学和动力学特性也受到关注, 在力学超材料的理论体系内,基于折纸/剪纸结构堆叠或组合而成的力学超材料几乎可以实现力学超材料的所有力学超常特性, 如负泊松比、多稳态、负刚度、各向异性等(Kamrava et al. 2017), 也展现出丰富的可调控、可编程特性, 并且可以实现对波动的调控(Babaee et al. 2016, Harne & Lynd 2016, Pratapa et al.2018). 因此, 折纸/剪纸技术为智能力学超材料提供了一种基于机构的强大设计平台(Bertoldi et al. 2017), 在振动与噪声控制方面也展现出良好的应用前景. (Zhu et al. 2019, Yasuda et al. 2019,Ji et al. 2021, Meloni et al. 2021)

在可编程、可调控力学超材料的基础上, 力学超材料设计的另一层级是在材料中引入传感器件用以感知外界环境, 并通过元胞中的作动器件改变材料力学性能, 实现材料对环境变化的自适应性. 在振动与噪声控制方面, 这一方面的研究通常与主动控制和智能材料技术进行交叉融合. 但与传统主动控制技术不同的是, 传统主动控制技术以波调控或结构动响应抵消为目标, 通过在系统中加入作动器件抵消外界激励对系统的作用; 而智能力学超材料以元胞结构及力学参数为调控对象, 实现对环境变化的自适应, 这就需要掌握元胞参数与宏观力学性能的定量关系,例如Akl 和Baz (2010)通过在传统霍姆赫兹共振腔底附加压电材料, 并通过调节压电材料两端电位差实现等效体模量的调节, Popa 等(2013), Popa 和Cummer (2014)进一步设计了可以调节等效密度和等效模量的主动微结构单元, 不仅扩宽了材料动态特性的调控范围, 还可以实现具有超常吸收、负折射、非互易等特性的力学超材料. 最近, Qi 等(2021)对主动力学超材料的元胞设计、多物理场调控性能和应用探索等方面的研究进展进行了总结, 本文不再详述.

另外, 随着机器学习、人工智能技术的发展, 基于智能算法的力学超材料智能化设计也成为助推领域发展的重要方向. 智能算法擅长于通过挖掘大量数据信息来寻找隐藏规律, 适用于解决数据丰富且深层物理机制不被完全掌握的问题, 特别是当该问题涉及到高度非线性机制时(Yang et al. 2018). 传统的实验和计算建模技术需要消耗大量的时间和资源, 且容易受到实验条件或理论基础的限制, 特别是对于拥有较大参数空间的模型, 从由大量参数描述的系统状态到行为表现的映射往往非常复杂. 基于AI 的力学超材料智能设计方法可利用强大的GPU 计算能力,进行数据挖掘和分析处理, 能高效地学习到对非线性复杂映射关系的描述, 极大地提高了材料表征和设计的经度和效率(Correa-Baena et al. 2018, Jiao & Alavi 2021). 因此, 基于智能算法的力学超材料智能设计方法 (设计思路如图50 所示) 被认为是加速力学超材料性能预测、拓扑结构优化设计和反向设计的有效手段(Olson 2000), 也是当前智能算法应用的重要方向.

基于机器学习的材料性能预测在近几年取得了一定进展(Pilania et al. 2013, Schütt et al.2014, Ward et al. 2016). 卷积神经网络 (CNN) 由于其特有的归纳偏差特性, 很适用于寻找材料结构-性能关系(Cohen & Shashua 2016, Battaglia et al. 2018). 该问题本质上是寻找结构和性能之间的高度非线性映射关系(Krizhevsky et al. 2017, He et al. 2016a). 例如, 在多孔材料的吸声系数预测问题上, 首先分层图像处理机制提供了特征提取的局部性, 因此适用于存在某些类型局部结构的多孔材料, 其次池化操作保证了空间不变性的特性, 因此它可以容忍局部结构的大量空间平移. Pilania 等(2013)等利用机器学习方法建立了材料系统参数和属性之间映射, 同传统模拟方法相比极大地提升了效率, 实现以小的成本预测材料性能.

由于卷积神经网络特别适用于处理图像数据, 智能算法在超材料拓扑结构设计和优化方面应用广泛(Mao et al. 2020, Donda et al. 2021, Zhang et al. 2021d). 结构功能材料的拓扑结构设计和优化是提升材料性能的一个重要途径. 当前, 基于图像输入的力学超材料智能设计大多利用了生成对抗网络 (GANs) , 如图51 所示. GANs 包括一个生成器 G 和一个判别器 D, 它们相互竞争. 这是一个“两人零和”游戏, G 旨在生成尽可能“真实”的“假”数据以“骗过”D, 而 D 则学会尽可能准确地将 G 生成的假数据与真实数据区分开来. 这本质上是一个 minmax 过程, 其中 G和 D 都可以分别提高他们的生成和判别能力(Goodfellow et al. 2014). 最终, 达到了纳什均衡,这意味着如果不改变其他玩家的策略, 每个玩家都无法获得更好的结果, 并且两个玩家保持同样的结果(Fedus et al. 2017). Zhang 等(2021d)利用GANs 特有的生成特性进行吸声多孔超材料的快速设计 (如图50 所示) , 并发现其具有生成全新材料构型和和丰富局部特征的显著能力. Mao等(2020)利用GANs 创建了一套设计复杂结构材料的系统方法, 以此创造全新的拓扑结构并对其进行优化, 同时利用此方法设计了孔隙度从0.05 到0.75 时各向同性弹性刚度接近Hashin-Shtrikman 上限的材料拓扑结构.

反向设计在物理、工程和材料等学科十分常见(Sanchez-Lengeling & Aspuru-Guzik 2018).同传统的反向设计 (遗传算法和伴随法) 相比, 机器学习因在数值模拟的高准确度和高效率等优势也被用于解决力学超材料反向设计问题(Liu et al. 2019). Ronellenfitsch 等(2019)提出了一种灵活的反向设计方法, 可以在离散力学超材料中实现一个或多个带隙位置的精确设计. 该方法的底层算法可直接优化弹性网络的线性响应, 适用于有序和无序结构, 同时可在二维和三维上实现高效缩放, 能与其他数值优化方案相结合. Oliveri 和Overvelde (2020)通过引入一种随机优化算法来探索反向设计问题, 针对超材料的屈曲特性进行了调整和设计. Zheng 等(2020b)提出了基于高斯-贝叶斯模型的机器学习算法对力学超材料进行反向设计, 该方法可针对特定功能需求有效地设计力学超材料的参数. Challapalli 等(2021) 基于GANs 搭建了一套轻质力学超材料的反向设计架构, 可以设计出比现有材料承载性能高40% ～ 120%的晶格超材料, 并可以被用于其他类型承载材料设计. 可以预见, 机器学习等先进智能方法将在力学超材料优化设计、特性机理挖掘、一体化集成应用等方面发挥重要作用.

6.2 声学/弹性拓扑材料和非厄米材料

近年来, 类比凝聚态物理领域拓扑态、拓扑绝缘体等概念, 在声学和弹性波系统中提出的拓扑态引起广泛重视, 其所具有的缺陷免疫、单向波导、背散射抑制等优异波调控特性, 可以用于实现对波传播和耗散的精准操控, 特别是其可以免疫结构中的缺陷和杂质, 在结构无损检测、高性能机械信号的探测与处理系统等方面具有应用前景(Ma et al. 2014). 陈毅等 (2021) 对声学、弹性波拓扑材料的基本理论、波调控机理和验证进行了较为详尽的介绍, 本文重点讨论其在结构弹性波控制和声场调控方面的设计思路和应用前景.

图50基于智能算法的力学超材料设计思路

图51基于生成对抗网络的力学超材料拓扑结构优化设计(Zhang et al. 2021d)

在一维声学/弹性系统中, 拓扑边界态的构造通常基于具有不同拓扑特性的力学超材料杂化实现, 如 Yin 等(2018) 在一维纵波和弯曲波结构系统中验证了在杂化边界处存在稳定的拓扑态.这类边界态具有强局域化和免疫几何缺陷等特性, 可用于实现可抵抗环境变化干扰的高可靠弹性波信号感知处理 (Zangeneh-Nejad & Fleury 2019), 如图52(a)所示. 另外, 拓扑绝缘体构造过程中新诱导体带隙以及边界态产生为结构隔振和能量收集等方面应用提供可能(Xia et al. 2020,Chaplain et al. 2020).

在二维系统中, 类比量子谷霍尔效应中的谷边界态、量子自旋霍尔效应中的螺旋边界态和高阶拓扑绝缘体中的角态等拓扑物态, 在弹性和声学系统中均能够构筑具有拓扑保护的边界态和高阶角态, 实现高效低损耗的波动操纵. Zhang 等(2018b)研究发现, 声波通过谷霍尔拓扑绝缘体将表现出超定向的针状声束天线模式, 如图52(b)所示, 可以实现杂波信号 (噪声) 的方向选择性屏蔽, 也可利用该声束实现目标方位的确定. 同样, 在水声领域也可以基于拓扑态形成高聚焦波束, 用于水声噪声抑制和水声目标探测定位等(Zheng et al. 2020c). 基于螺旋边界态具有的自旋动量锁定的单向波导特性, He 等(2016b)设计了具有波传播方向选择性的交叉波导分流器,可应用于集成声学信号开关设计, 实现特定通道声波信号的导通和阻止. 在弹性拓扑材料中, 通过调节晶格的结构参数能够实现赝自旋非平庸拓扑相, 例如晶胞的收缩扩张(Yu et al. 2018)、散射体的旋转(郑周甫等 2020)等, 这些设计为结构振动传播路径的精确调控提供了思路. 同时,螺旋边界态具有拓扑保护波导耦合谐振特性, 利于相干储能、相干源等基于相干增强的弹性谐振器实现(Yu et al. 2018, 2021b).

图52力学超材料的拓扑态及波调控应用. (a)基于弹性波精确调控的信号处理器件(Zangeneh-Nejad&Fleury 2019), (b)定向噪声屏蔽(Zhang et al. 2018c), (c)弹性波亚波长高阶拓扑态及其维度转换现象(Zheng et al. 2022)

近年来, 高阶拓扑绝缘体成为拓扑物理领域研究的热点. 高阶拓扑绝缘体能够同时实现多个维度的拓扑态, 例如二维高阶拓扑绝缘体同时存在具有带隙的1 维边界态和0 维角态(Serra-Garcia et al. 2018, Fan et al. 2019, Ni et al. 2019, Xue et al. 2019). 高阶拓扑态不仅拓展了拓扑材料的范围, 还反映出了晶体对称性与能带拓扑之间复杂的相互作用(Xie et al. 2021), 为不同维度边界提供了拓扑波调控能力. 当前, 在高阶拓扑材料方面, 不断有研究突破常规晶格对称性限制, 能够在任意指定角落灵活实现能量局域(Wu et al. 2021, Zhang et al. 2021e). Zheng 等(2022)基于局域共振力学超材料, 在板结构中实现了亚波长频段的弹性波高阶拓扑态, 并发现了杂化结构中的频率选择性激发和维度转换现象(如图52(c)所示), 构建了灵活的亚波长弹性波调控平台. 这些工作对于构建具有波能量捕获、控制、传感和激射能力的声表面波集成化和微型化器件等方面具有应用前景, 将有助于推进拓扑材料的实际工程应用.

通常在动力学分析中, 具有实数本征值的模态都是由仅有实数材料参数的模型 (厄米模型)得到, 含材料参数虚部 (有损耗或增益) 的模型 (非厄米模型) 不存在实数本征值的模态.1998 年, Bender 和Boettcher 发现, 在具有宇称-时间对称性 (Parity-time symmetry) 的非厄米模型中, 系统的哈密顿量可以存在实数的本征值(Bender & Boettcher 1998). 这意味着通过调节材料的损耗和增益, 在电磁、弹性介质非厄米模型中保持PT 对称性, 同样可以实现对电磁或力学特性的调控. 研究表明, 这样的动力学系统可以得到与传统厄米弹性理论体系不同的调控方式和效应, 如非零几何相位(Gong & Wang 2010)、单向衍射(Lin et al. 2011), 激射和完美吸收共存(Chong et al. 2011)等.

2015 年, Fleury 等(2015)结合电路反馈系统、麦克风和扬声器等构建等效声学增益介质,研究了该超材料的反常声散射特性, 实现了基于PT 对称性的非厄米声学相干完美吸收效应, 并利用该效应设计了在高效接受传感信号的同时不扰动外部环境的声学传感器, 如图53 所示, 展示了非厄米PT 对称超材料在声学、损耗补偿和超常波处理方面的独特相关性. 2017 年, Zhao等(2016)在由硅橡胶和环氧树脂组成的一维超材料模型中引入损耗和增益, 研究超材料的局域共振模式在非厄米模型中的特性, 分析表明在满足PT 对称时, 局域共振模式出现散射矩阵简并点分裂效应, 局域共振P 模式和 D 模式对应的本征值两重简并点发生分裂, 变成一对两重简并点, 该效应可以用于设计高 Q 值的声传感器.

随研究的深入, 非厄米模型被逐渐引入到变换声学、拓扑声学、相位梯度超表面等超材料的前沿领域. 研究者在满足PT 对称性的复弹性模量表达式中引入坐标变换(Zhu et al. 2013), 分析了坐标变换后弹性介质的张量表达式, 得到能够实现非互易隐身效果的宇称时间对称声隐身斗篷和隐身地毯设计模型, 结果表明隐身效果可随损耗因子的变化而变化, 即非厄米模型在声隐身效果的调节方面引入了新的自由度, 能够拓展基于超材料的声隐身设计理论. Wang 等(2018)在无损谷输运超材料中引入增益 (gain) 和损耗 (loss) 单元, 得到支持弹性波衰减或增益传播的,具有涡旋声场分布的谷态、谷能带投影边界态等新的超材料动力学模式, 揭示了在非厄米系统中引入拓扑保护“谷输运”的声调控机制, 该工作对于探索强度可控的谷态运输和谷传输中继(relay) 提供了新的思路. 在非互易传输系统设计方面, 非厄米体系也展示了巨大的潜力. 基于相干完美吸收效应, Zhang 等(2019)在二阶声拓扑绝缘体中引入增益和损耗单元, 构造了非厄米共轭的声学二阶拓扑绝缘体 (如图54 所示) , 得到PT 对称性破缺的声衰减角态和声增强角态, 能够通过改变非厄米强度调节角态能量的衰减或增强, 在系统损耗与边界态本征辐射率相匹配时,在拓扑边界态中得到奇异的非互易模式, 能够实现单向的完美吸收与全反射并存的超材料设计.该工作将拓扑声学的理论与PT 对称声学相联系, 为非厄米系统中的声传输操控设计提供了新的思路. Wang 等(2019b)在无损耗相位梯度超表面的特定基元中引入黏滞损耗效应, 构造了二通道的非厄米超表面模型, 研究表明通过相位梯度和基元损耗的调节, 该超表面声散射矩阵的本征值及本征矢量能够在一定的频率实现简并, 产生非厄米系统的奇异点, 这同样能够实现单向完美吸收与全反射并存的非互易弹性波调控.

非厄米超材料通过精细调控微结构单元中的损耗或增益效来调节材料整体的力学特性, 为弹性波或机械特性的调节提供了额外的自由度, 展现了单向声隐身、单向声局域和声学系统散射矩阵简并点分裂、强度可调谷输运等在无损系统中难以实现且具有理论探索价值和潜在应用前景的新效应, 为新型声学、力学结构及器件研究开拓了新的思路.

7 结论及展望

图53基于PT 对称性超材料的声传感器模型 (Fleury et al. 2015)

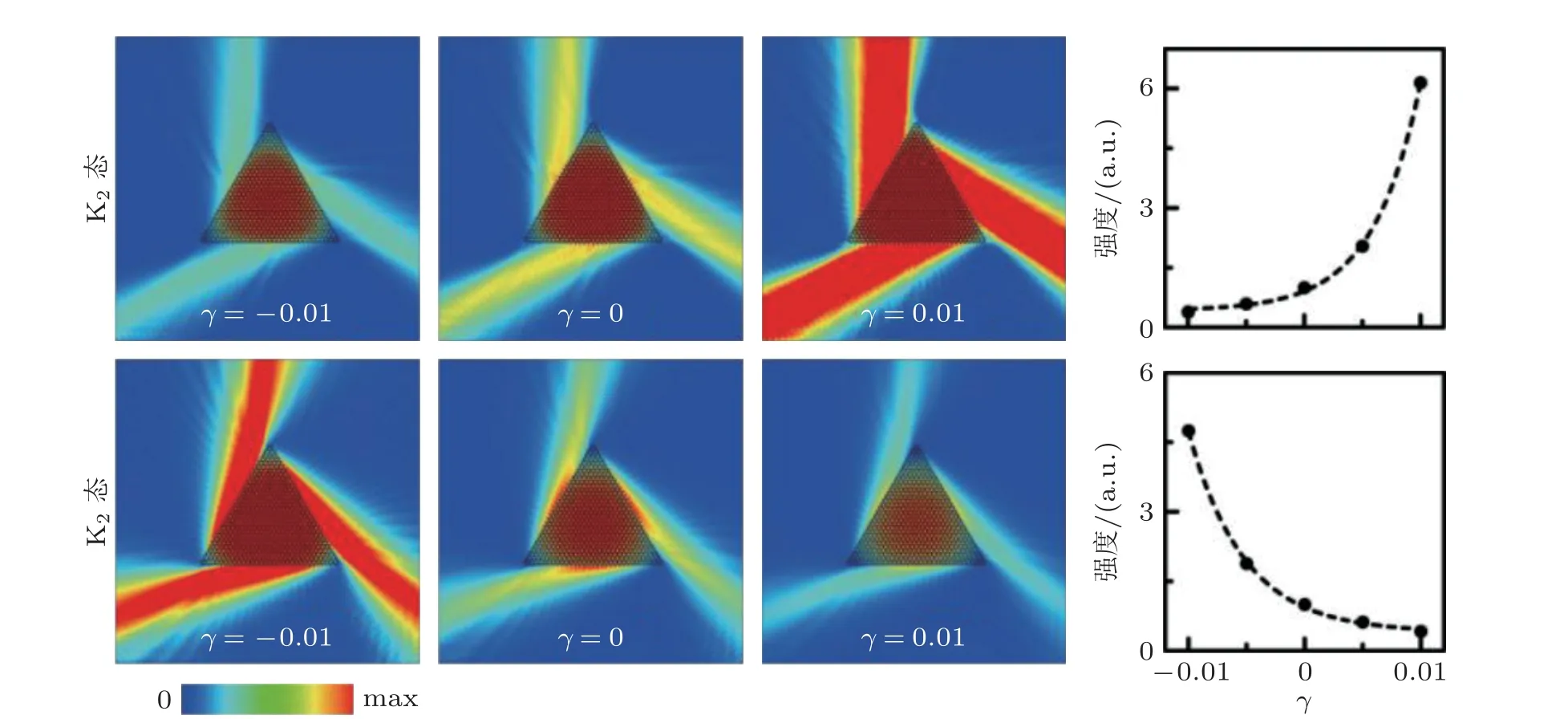
图54包含增益或损耗特性的非厄米超材料谷态的声场模式 (Zhang et al. 2019)

实现“材料-结构-功能”一体化设计是未来工程领域发展的重要方向, 力学超材料丰富的力学特性为推动这一方向的发展提供了可行的思路. 本文以 “功能”需求为主线, 系统讨论了力学超材料在装备/结构振动、冲击及噪声控制方面应用研究的最新进展. 首先简要回顾了力学超材料概念的起源、理论体系的建立和发展, 接着总体介绍了力学超材料在动态波调控和静态力学性能调控方面的典型超常特性, 进而在第3 ～ 5 节中分别围绕水声隐身、空气声降噪和减振抗冲应用背景, 重点介绍了力学超材料在低频、宽带、精确声振调控方面取得的研究进展. 最后, 介绍了包括可编程及智能力学超材料、非厄米和拓扑材料等几类新颖力学超材料的研究概况和应用前景.

目前来看, 力学超材料已经形成了较为完善的理论体系、分析方法和设计思路, 为实现振动与噪声控制工程应用的实用化提供了有力支撑. 面向实际应用和未来发展, 可以从以下方面进一步拓展:

力学超材料的新机理新效应研究: 学科交叉融合是推动力学超材料发展和工程应用的不竭源泉. 近期发展起来的非厄米、拓扑态、声非阿贝尔拓扑荷等新奇物态使得力学超材料波调控机理不断扩展, 为结构弹性波和声场精确控制提供了多样化的实现思路.

力学超材料的低频宽带设计: 力学超材料的窄带效应和固有损耗是限制其工程应用的重要因素, 因此, 实现低频宽带是减振降噪工程应用必须突破的关键问题; 在实际应用中, 还需要考虑多方面的工程约束条件 (厚度、密度、耐压等) , 这些因素都为力学超材料设计带来更大挑战. 这一方面的主要发展方向一是研究多机理耦合的力学超材料低频宽带波控技术, 另外是发展复杂工程约束条件下力学超材料多功能一体化优化设计理论与方法.

力学超材料多尺度多层级设计: 3D 打印等先进制造技术的发展为制备具有多尺度、多层级特点的力学超材料提供了条件, 不同尺度单元的耦合不仅使整体结构更加复杂, 还会带来更多新颖的力学属性、更宽广的性能调控空间、更灵活的设计自由度. 将多尺度多层级设计思想应用于抑振、抗冲、降噪结构与材料设计, 可以有效提升声振调控性能, 是未来力学超材料研究的重要方向之一.

力学超材料的智能主动设计. 人工智能和智能材料等领域的飞速发展也为力学超材料研究带了新的机遇, 体现在力学超材料设计的智能化、力学超材料性能的智能主动可调设计、力学超材料的智能制造技术等. 材料的智能化使其在减振降噪领域具有更灵活的适应性和可调性, 对于工作在复杂力学环境下的装备声振安全设计具有重要意义.

总之, 力学超材料作为多个领域和学科方向研究的热点, 展现出丰富的研究价值和良好的工程应用前景. 在振动与噪声控制工程领域, 国内外已经开展不少有益的探索, 并取得了成功的应用案例. 在应用推进中, 仍有诸多关键理论和技术问题值得广大科研人员深入研究.

致 谢 国家自然科学基金(11991030, 11991032, 11991034, 11872371) , 湖南省科技创新领军人才项目(2022RC4022)资助项目.