神经系统疾病与认知动力学(II):神经振荡与认知动力学

韩 芳 樊登贵 张丽媛 王青云 顾晓春 王直杰

1 东华大学信息科学与技术学院, 上海 201620

2 北京科技大学数理学院, 北京 100083

3 北京工业大学环境与生命学部, 北京 100124

4 北京航空航天大学航空科学与工程学院, 北京 100191

5 上海电机学院, 上海 200245

1 引 言

神经振荡, 又称脑波, 是大脑神经系统中存在的一种节律性或重复性的神经活动. 神经振荡在神经系统中普遍存在, 其源于潜在的生理机制的非线性相互作用 (Glass 2001) , 以在时间尺度上组织神经元同步放电的方式在特定区域、特定的频段发生 (Senkowski et al. 2008, Siegel et al.2012, Trujillo et al. 2019) , 被认为是实现多种脑功能 (Schnitzler & Gross 2005, Kopell et al.2014) 的内在基础, 受到了广泛的关注. 神经振荡包含多种类型 (Cole & Voytek 2017 ) , 其频谱波段跨度为0.5 ～ 600 Hz (Buzsáki & Draguhn 2004, Buzsáki 2006) , 其中伽马振荡 (30 ～ 90 Hz)被认为是与高级的脑功能 (认知功能) 关系较密切的一种神经活动 (Buzsáki & Wang 2012) , 在过去的几十年里引起了认知神经科学领域特别的关注. 自Adrian (1942) 首次在麻醉刺猬的嗅球上发现由感觉刺激诱导的伽马振荡后, 研究者们掀起了一系列对伽马振荡的研究热潮, 从动物脑到人脑、从局部脑到整个脑, 试图使用各种研究方法揭示大脑中伽马振荡的奥秘. 目前, 在特征结合、注意选择或工作记忆维持等认知作用过程中, 已经在多个物种的不同大脑区域观察到伽马振荡 (Pesaran et al. 2002, Bauer et al. 2014) . 伽马振荡的改变也被报道与神经生理和精神疾病有关, 如精神分裂症 (Jadi et al. 2016) 和抑郁症 (Fitzgerald & Watson 2018) 等, 但它们确切的参与作用和潜在机制尚未完全了解.

当前, 脑电中的高频伽马振荡的生理学研究结果多是在刺激信号固定的情况下被发现的, 其振荡频率也是固定的. 但是神经生物学实验进一步发现, 不同特征的刺激信号如不同的对比度图像信号 (Henrie & Shapley 2005; Adjamian et al. 2008; Ray & Maunsell 2010; Jia et al. 2013a,2013b) 、不同大小的刺激 (Henrie et al. 2005, Gieselmann & Thiele 2008, Ray & Maunsell 2011) 、运动视觉信号 (Swettenham et al. 2009, Muthukumaraswamy & Singh 2013, Orekhova et al.2015) 以及图像声音混合信号 (Hipp et al. 2011) 等均可引发不同频率的伽马振荡, 即该伽马振荡的频率随着刺激信号特征的变化而敏感地变化. 然而, 这种频率敏感依赖于刺激输入的伽马振荡的产生机理及其潜在的认知功能至今未明. 高频伽马振荡的产生通常与外部刺激有关, 因此研究刺激引发的伽马振荡的产生及其认知机制对揭示大脑神经系统的信息处理原理具有重要的作用, 对类脑智能的研究亦具有重要的参考价值.

近几十年来, 认知神经科学家们通过各种方法研究这种复杂的神经非线性动力学行为和大脑认知功能之间的关系, 并取得了一些有价值的成果. 研究神经振荡的方法主要有两种: 一种是生物学实验研究, 即运用各种生物实验方法和技术对人脑和动物脑进行科学实验 (Bragin et al.1995, Whittington et al. 1995, Bartos et al. 2002, Osipova et al. 2006, Sato et al. 2019, Bitzenhofer et al. 2020) , 如通过视觉刺激动物或人类受试者后, 使用电极、脑电图、放大器和示波器等实验技术观测脑电活动 (Gruber et al. 1999, Muthukumaraswamy & Singh 2013, Magazzini & Singh 2018, Peter et al. 2021) ; 另一种是理论建模研究 (Aoyagi et al. 2002; Bathellier et al. 2006, 2008;Jia et al. 2013a, 2013b; Oliveira et al. 2019; Sherfey et al. 2020) , 即通过建模分析和计算机模拟,建立各种生物神经网络模型并对网络活动进行模拟仿真, 重现生物学实验结果并对其产生及信息处理机制进行研究. 神经振荡是大量神经元同步放电的结果, 在伽马振荡的形成中, 抑制性神经集群同步放电发挥了重要作用 (Tiesinga & Sejnowski 2009) , 因此对伽马振荡的理论建模往往通过建立兴奋性/抑制性 (Excitatory/Inhibitory, E/I) 神经网络并研究其同步放电来进行. 作为神经振荡形成的基础, 神经同步被认为在神经通信中起着至关重要的作用, 推测认为, 神经通信是通过临时组织的神经集群来实现的, 神经元放电的精确时间是通过同步来协调的 (Buzsáki 2004, Buzsáki 2006) . Fries (2015) 提出的同步通信假说有力地论证了伽马同步振荡与高级脑功能之间的关系. 因此, 阐明伽马振荡模式是如何产生和调节的, 对于理解大脑认知具有至关重要的意义.

图1神经振荡的脑电节律

本文首先对生物学实验研究中发现的不同类型的神经振荡及其功能、特别是伽马振荡及其认知功能的研究现状进行阐述, 然后针对实验中发现的依赖于刺激特征的变频率伽马振荡现象,综述基于神经网络模型的伽马振荡产生机理及其认知功能的动力学建模研究工作.

2 基于生物学实验的神经振荡及其功能研究

2.1 神经振荡及其功能

神经科学家们在动物实验中使用脑电图 (EEG) 、脑磁图 (MEG) 或局部场电位 (local field potential, LFP) 等记录方法, 在动物清醒或睡眠期间的各种行为状态下发现了从慢波振荡到快波振荡多种神经振荡模式, 并根据不同的频率段将神经振荡分为以下几种类型 (Kropotov 2009)(如图1 所示) : 德尔塔振荡 (0.5 ～ 4 Hz) 、西塔振荡 (4 ～ 8 Hz) 、 阿尔法振荡 (8 ～ 12 Hz) 、贝塔振荡 (12 ～ 30 Hz) 、伽马振荡 (30 ～ 90 Hz) 和超快振荡 (90 ～ 200 Hz) . 这些不同类型的神经振荡存在于不同的脑区, 且反映出大脑不同的行为状态, 被认为参与了大脑多种功能的实现.

阿尔法振荡是第一个被人类发现的脑波振荡, 出现在大脑低级皮层和丘脑核, 通常被认为是一种存有记忆、知觉和情绪的潜意识状态 (Bremer 1958, Buzsáki 2006) .

西塔振荡是第一个被认为和脑功能有着重要关联的脑波, 主要出现在海马区以及与海马区有连接的区域, 如额外皮层、前额叶皮层和丘脑等, 被认为在情节和空间记忆的形成及恢复中起着一定的作用 (Vanderwolf 1969, Bland & Brian 1986) , 同时在学习和记忆过程中也起到关键的作用 (Kahana et al. 1999, Jensen & Tesche 2010) .

贝塔振荡与运动行为相关 (Buzsáki 2006) , 如贝塔振荡被发现发生在癫痫的 “准备期间”(Jasper & Penfield 1949) , 但又有实验发现贝塔振荡可能和认知过程也有关系 (Grossberg &Versace 2008) .

德尔塔振荡是大脑中较缓慢的脑波, 一般在“无意识”状态下产生, 而且出现在非快速动眼睡眠 (non-rapid eye movements, NREM) 的第三阶段 (Buzsáki 2006) . 德尔塔振荡在慢波睡眠中是明显的, 如果在非睡眠时出现德尔塔振荡, 则表明大脑可能存在异常情况.

高频超快振荡主要存在于小脑、海马体和大脑新皮层 (Adrian 1935, Buzsáki et al. 1992,Canolty et al. 2006) . 目前对于超快振荡的产生机理及其功能知之甚少.

伽马振荡最早也是由Adrian (1942) 发现的 (Adrian 同时也是超快振荡的发现者) . 之后, 加州大学的 Freeman (1975) 发现伽马振荡的基础在于兴奋性和抑制性神经元群之间连接突触的相互作用, 这是生物学实验研究史上揭秘伽马振荡产生机理的一个重要研究成果 (Tiesinga &Sejnowski 2009) , 之后的建模研究也验证了这一结论. 许多生物学实验表明伽马振荡是大脑功能特别是认知功能的反映, 更重要的是它参与了一些认知功能的调节如学习与记忆. 另外, 不规则的伽马振荡是认知障碍类疾病如精神分裂症、孤独症和语言学习障碍等的标志.

2.2 伽马振荡及其认知功能

伽马振荡因其与大脑的多种认知功能和各种令人困扰的神经现象密切相关而备受关注, 所以在生物实验中得到了更为广泛的研究. 目前伽马振荡已在视觉区、嗅觉区、海马区和新皮层等许多脑区中被发现, 被认为是反映大脑各个区域神经环路多种认知功能的标志, 如特征绑定、感觉信号的加工与处理、注意机制、学习与记忆、神经信息通讯和编码等. 举例来说, 生物学实验研究发现伽马振荡从一定程度上能反映刺激的特征, 具有特征绑定作用 (Singer & Gray 1995);有研究表明伽马振荡参与了人脑感知觉的形成过程 (Kaiser & Bühler 2004) ; 伽马振荡最初还被称为是“超警觉”的节律, 因为它与动物高度警觉的大脑状态相关 (Bouyer et al. 1981) ; 人体研究中的脑电图 EEG 和脑磁图 MEG 记录也表明, 注意力与增加的伽马节律有关 (Fries et al. 2001,Schroeder & Lakatos 2009) ; 此外, 生物学实验研究也记录到了各种感觉形态中与注意力相关的伽马振荡: 听觉 (Sokolov et al. 1999, Fan et al. 2007) 、视觉 (Doesburg et al. 2008, Siegel et al.2008) 、体感 (Hauck et al. 2007, Koch et al. 2009) 和疼痛 (Hauck et al. 2007, Tan et al. 2021) 等;人类研究中的 MEG、EEG 和颅内脑电图记录 (iEEG) 显示, 顶叶、额叶和其他皮层区域存在着强烈的伽马振荡, 与工作记忆密切相关 (Howard et al. 2003, Jerbi et al. 2008) ; 啮齿类动物的抑郁状态会导致大脑相关脑区伽马同步活动异常, 通过一些有效治疗手段 (例如深部脑刺激治疗) 其相关脑区伽马节律振荡又会恢复, 因此伽马振荡是动物抑郁状态的重要生物学标志(Gazit et al. 2015, Khalid et al. 2016) .

由于伽马振荡在认知功能上的重要作用, 神经科学家们越来越重视对伽马振荡的研究. 虽然伽马振荡已在多个脑区被发现, 但是如果同时对多个脑区神经系统的伽马振荡进行研究将是异常困难的. 视觉系统是功能最复杂的感觉系统, 它接收和处理日常生活中的大部分信息, 并牵连着大多数皮层区域, 而初级视觉皮层 (V1 区) 是视觉皮层处理层次中的第一层区域, 它整合来自外侧膝状体核 (lateral geniculate nucleus, LGN) 和视网膜的输入信息, 并将它们投射到更高的皮层区域, 所以, V1 区是较高认知功能与较低感知活动相关联的关键结构区. 因此, 很多生物学实验将焦点集中于视觉皮层, 尤其是 V1 区的伽马振荡研究, 发现不同的刺激方式能够引起视觉皮层的伽马振荡. 在视觉皮层的研究中, 刺激诱发的伽马振荡最先是由 Gray 等 (1989) 在麻醉猫的初级视觉皮层 (V1 区) 和第二视觉皮层 (V2 区) 发现的; Frien 等 (1994) 在清醒的猴子视觉皮层的 V1 区和 V2 区也观察到了伽马振荡; Tallon 等 (1998) 在受试者探测模糊图片中的图像时, 通过脑电图 (EGG) 记录发现了受试者视觉皮层中增强的伽马振荡. 之后, 更多的神经生物学实验表明视觉刺激能够引起 V1 视觉区的伽马振荡 (Schwarzkopf et al. 2012, Xing et al. 2012, Brunet et al. 2014, Bastos et al. 2014, Vinck et al. 2015, Storchi et al. 2017) .

以上生理学研究结果大多是在刺激信号固定情况下发现的, 相应伽马振荡的振荡频率也是固定的, 而后来的神经生物学实验研究进一步发现刺激的特征对伽马振荡的频率具有调控作用.Henrie 等 (2005) 发现 V1 区的伽马振荡的频率随着对比度的增强而增大; Adjamian 等 (2008)发现 V1 区的伽马振荡和灰度对比度有关, 和颜色对比度无关; Ray 和Maunsell (2010) 发现猴子在完成识别光栅朝向任务产生的伽马振荡的振荡频率随光栅对比度的增强而增大; Xing 等(2012) 在猴体上发现对比度诱发的伽马振荡集中在V1 的L2/3 和L4B; Jia 等 (2013b) 发现视觉刺激产生的伽马振荡的能量随光栅增大或对比度变大而增强, 而峰值频率随光栅增大而减小、随对比度增大而增大; Saleem 等 (2017) 在小鼠V1 区和LGN 上均发现亮度诱发的伽马振荡, 其强度与亮度正相关, 与对比度呈反相关; Perry 等 (2015) 和 Saleem 等 (2017) 在视觉皮层中发现随着刺激对比度或光强度的增大, 伽马振荡的频率和强度呈线性增长. 伽马振荡的频率还被发现和刺激的运动速度正相关 (Swettenham et al. 2009, Muthukumaraswamy & Singh 2013, Orekhova et al. 2015) , 和刺激的大小负相关 (Henrie et al. 2005, Gieselmann & Thiele 2008, Ray &Maunsell 2011), 和刺激距离视网膜中心的离心率正相关 (Gregory et al. 2016) . 其次, 生物学实验研究还进一步发现刺激的类型对伽马振荡的频率也具有调控作用. Demiralp 等 (2007) 在受试者辨别图像时, 发现了频率为 40 Hz 左右的伽马振荡; Hipp 等 (2011) 在受试者感知到视觉与听觉混合信号时, 发现了频率为 64 ～ 128 Hz 的伽马振荡. 以上生物学实验依据表明不同特征的刺激信号如不同的对比度图像信号 (Henrie & Shapley 2005; Adjamian et al. 2008; Ray & Maunsell 2010; Jia et al. 2013a,2013b) 、不同大小的刺激 (Henrie et al. 2005, Gieselmann & Thiele 2008, Ray & Maunsell 2011) 、运动视觉信号 (Swettenham et al. 2009, Muthukumaraswamy &Singh 2013, Orekhova et al. 2015) 以及图像声音混合信号 (Hipp et al. 2011) 等可以引发不同频率的伽马振荡.

大量有关伽马振荡的神经生物学实验只有很少现象能够得到理论研究和证实, 而上述依赖于刺激信号特征的变频率伽马 振荡的产生机理及潜在的认知功能至今未明, 本文将针对此现象开展理论建模研究工作, 对于视觉刺激引发变频率伽马振荡的现象给出动力学机理解释并对变频率伽马振荡的认知功能做出假设验证.

3 基于生物神经网络模型的伽马振荡及其认知功能研究

为了理解刺激引发伽马振荡的生物学实验结果并揭示其产生机理及潜在的认知功能, 需要从理论上解释几个难点问题: 各种特征的刺激信号是如何引起伽马振荡的？伽马振荡的振荡频率是如何随刺激信号特征的变化而敏感变化的？依赖于刺激特征的变频率伽马振荡有着怎样的认知功能？针对这些难点问题, 有必要采用理论建模的方法作进一步的研究. 在本节中, 首先综述理论建模所需的生物神经网络模型, 然后综述伽马振荡及其认知功能的理论建模方面的研究成果, 其中着重阐述近年来所开展的针对依赖于刺激的变频率伽马同步振荡及其认知功能的研究工作.

3.1 生物神经网络模型

大脑神经网络是一个极其复杂的系统, 它由数千亿个神经元组成, 每个神经元连接着成千上万条突触, 这些神经元和突触具有非常复杂的动力学特性, 并在不同脑区组成了具有各种复杂结构的神经回路. 为了对脑区各种振荡现象的产生机理进行研究, 需要对脑区的生物神经系统进行建模和模拟仿真, 因此建立完整且尽量逼真的神经网络计算模型至关重要, 包括神经元模型、突触模型、具有各种拓扑结构的网络模型以及外部刺激模型等.

神经元模型可以将神经元放电的动态过程以数学计算的方式描述出来. Hodgkin 和 Huxley(1952) 提出了Hodgkin-Huxley (HH) 模型, 揭示了神经元离子活动的规律及动作电位的产生机理, 并因此获得了诺贝尔奖. 但早在动作电位的产生机理被理解之前, Integrate-and-Fire (IAF)模型 (Lapicque 1907) 就描述了生物神经元的基本放电特性. 此外, MP 神经元模型 (McCulloch& Pitts 1943) 也能简单地反映出神经元的空间整合和阈值之间的非线性关系. HH 模型是四维动力学方程, 不能用二维平面相图直观地表达出来, 后来提出的FHN 模型 (FitzHugh 1961) 能简洁而准确地反映神经元放电活动的主要特征. 随着人们对神经元模型的研究逐渐深入, 又得出了不仅能模拟神经放电的动作电位、还能模拟神经放电的频率特性的HR 模型 (Hindmarsh &Rose 1982) . 对于大规模的神经网络的模拟, 既要保证计算上的可行性, 又要尽可能地保持生物学上的合理性, 对HH 模型简化后的Izhikevich 神经元模型 (Izhikevich 2003) 能够在二者之间取得平衡, 具有比IAF 模型更高的准确度, 计算起来却比HH 模型更加简便.

E/I 神经网络模型由E 神经元和I 神经元组成 (Wallace et al. 2011, Neymotin et al. 2011) ,在研究中, 采用Integrate-and-Fire (IAF) 神经元模型来描述神经元兴奋或抑制的动力学特性, 其计算方程 (动力学模型) 如下 (Sacerdote & Giraudo 2013)

突触是神经元之间相互接触和通信的媒介, 突触计算模型包含更多的生物细节以实现突触真实精确的信息传递动态. 配体门控通道突触模型 (Rall 1967) 将突触神经递质的释放、扩散和与受体结合等一系列过程简化为一个突触后的时间依赖的配体门控通道. 随后又提出了描述突触配体门控通道的开放和关闭两种状态的马尔可夫动力学模型 (Markov kinetic model) (Destexhe et al. 1998) . 基于化学性突触复杂的动态特性, 递质-受体 (neurotransmitter-receptor) 离子通道动力学模型 (Chapeau & Chambet 1995) 能准确计算出突触在任意时刻的电导系数及离子通道水平等突触状态变量, 更真实且更完整地模拟了化学性突触离子通道门控动力学过程、突触电导的动态过程和突触信息传递的细节特征, 适用于不同水平的神经网络模型的建立. 但是出于对模拟仿真有效性考虑, 现代突触模型在此基础上进行了大幅度简化, 广泛使用的有基于电导的突触模型和基于电流的突触模型 (Dayan & Abbott 2001) : 基于电流的突触模型忽略了突触后膜电位对突触的影响, 每个神经元的动作电位引发不同突触后神经元相同的突触电流, 产生的突触电流强度与突触权值成正比; 基于电导的突触模型则更详细地考虑了突触后神经元的状态对突触的影响, 每个突触前神经元的动作电位对不同的突触后神经元引发不同的突触电流.

在神经网络建模中一般采用基于电导的突触模型, 其计算方程 (动力学模型) 如下 (Wang &Buzsáki 1996, Dayan & Abbott 2001)

针对不同规模的生物神经网络, 采用合适的网络拓扑结构对神经网络模型的准确表达和仿真是至关重要的. 为了方便调整小规模神经网络模型的神经元和突触数量等参数, 平衡随机网络结构 (Morrison et al. 2007) 被广泛采用. 而大规模神经网络模型中的神经元和突触数量庞大, 难以精准描述每一条神经元的连接, 现在广泛采用功能柱状的网络拓扑结构进行建模, 比如采用多层立柱结构建立初级视觉皮层的局部网络模型 (Neymotin et al. 2011) .

3.2 神经系统的伽马振荡动力学

针对神经生物学实验中发现的伽马振荡现象, 人们基于神经网络模型开展了大量理论建模研究, 目前对于固定频率的伽马振荡的产生机理已经有比较丰富的研究成果 (Vida et al. 2006;Bartos et al. 2007; Bathellier et al. 2008; Tiesinga & Sejnowski 2009; Wallace et al. 2011; Buzśaki& Wang 2012; Jadi & Sejnowski 2014a, 2014b;César et al. 2019; Lu et al. 2020; Li et al. 2021) ,最主要的有三种: ING 机理、PING 机理和不规则集群放电涌现机理, 其中前两种广为人知.

(1) 抑制性网络中伽马振荡的产生机理-ING机理

Bartos 等 (2007) 和 Tiesinga 等 (2009) 通过建模研究提出了伽马振荡的产生机理-“inter-neuron-Gamma (ING)” 机理. ING 机理认为高频同步伽马振荡主要由抑制性中间神经元集群引起, 抑制性神经网络能独立引起抑制性神经元的同步, 这些同步的抑制性神经元产生同步的抑制性突触电流, 经突触传递延时后传递到抑制性神经元集群, 阻止了抑制性神经元集群的放电而形成振荡周期中的静息期, 抑制性神经元集群只有在抑制性突触电流充分衰减后才能恢复放电而形成放电期. 因此, 根据 ING 机理, 同步振荡的频率主要由抑制性突触电流的衰减速度决定. 之后的建模研究又发现高频同步伽马振荡能够在一定异质程度的网络 (如神经元的输入异质、神经元的参数异质) 中产生, 并发现了分流抑制 (shunting inhibition) 机理 (Vida et al.2006) 和突触电流的形状机理 (Wang et al. 2011) 两种鲁棒同步机理.

(2) 兴奋性/抑制性网络中伽马振荡的产生机理-PING机理

Vida 等 (2006) 的建模研究提出了另一种高频同步伽马振荡的产生机理, 即 “pyramidal-interneuron-Gamma (PING)” 机理. PING 机理认为高频同步伽马振荡由兴奋性神经元 (E 神经元) 和抑制性神经元 (I 神经元) 相互作用形成. E 神经元的同步放电比 I 神经元的同步放电快一小段时间 (几毫秒) . 其同步的动力学过程为: 同步的 E 神经元放电, 经突触传递延时后, 其引起的突触后电流到达 I 神经元及E 神经元自身, 从而引起 I 神经元放电, 再经突触传递延时后, I神经元放电引起的突触后电流到达 E 神经元及 I 神经元自身, 从而阻止E 神经元及 I 神经元的放电而形成振荡周期中的静息期, E 神经元和 I 神经元只有在抑制性突触电流充分衰减后才能恢复放电而形成放电周期. 因此, 同步振荡的频率由抑制性突触电流衰减速度和兴奋性突触电流衰减速度共同决定. 并且, 当同步发生时, 突触电流处于上升阶段, 因此 E/I 网络中的高频同步振荡也具有鲁棒性.

(3) 由神经元不规则集群放电涌现的伽马振荡的产生机理

(1) 和 (2) 中讨论的同步振荡现象是网络中所有神经元 (或固定部分的神经元) 在每个振荡周期中的放电期都放电, 在静息期中所有神经元都静息. 另一同步振荡现象是网络中单个神经元的放电行为没有规律, 振荡的产生是不规则神经元放电的群体涌现结果 (Wang 2010, Buzśaki &Wang 2012) . Bathellier 等 (2008) 在一个抑制性网络中揭示了这种振荡现象的同步机理. 由于神经元放电率的不同, 部分神经元在某一振荡周期的放电期首先放电, 在突触延时较小的情况下,这些抑制性神经元的放电迅速抑制了剩余神经元的放电, 造成了在这个放电周期只有部分神经元放电, 这些刚放过电的神经元在下一周期又先放电的可能性比较小, 因此下一周期将是网络中另一部分神经元放电. Jadi 和Sejnowski (2014b) 、Wallace 等 (2011) 在放电率模型中也揭示了这种不规则神经元放电的群体涌现形成的同步伽马振荡现象.

上述讨论都是假设了神经元的输入是相同的或是具有较小程度的异质, 且产生的同步伽马振荡的频率是固定的. 而实际的大脑神经系统中的神经元的输入对应于真实的外部刺激, 因此各个神经元的输入是承载有信息的, 可能具有较高的差异性, 对这种携带信息的输入刺激作用下的异质神经网络的伽马振荡的动力学机理研究还很少见. 一些文献虽然研究了各种输入信号对同步振荡的调控作用, 但他们的研究针对的是低频率的阿尔法振荡 (Lefebvre et al. 2015, Herrmann et al. 2016, Hutt et al. 2016) . 而如2.2 节所述, 在神经生物学实验中发现伽马振荡的振荡频率随着刺激信号特征的变化而敏感地变化, 这种变化的频率应该携带了外部刺激的信息, 这类伽马振荡的产生机理及其潜在的认知功能尚不清楚. 目前在这方面的建模研究仅有个别的研究成果. Jadi 和 Sejnowski (2014a, 2014b) 构建了一个由简单的随机神经元构成的兴奋性/抑制性神经网络, 伽马振荡的产生遵从 PING 机理 (即由兴奋性神经元和抑制性神经元相互作用产生) .视觉输入信号可激励兴奋性神经元和抑制性神经元, 如果增强视觉信号对兴奋性神经元的输入,则峰值振荡频率提高但峰值振荡频率对应的振荡功率减小; 如果增强视觉信号对抑制性神经元的输入, 则峰值振荡频率降低但对应的振荡功率增大. 同时, 如果视觉刺激特征的对比度增大则峰值振荡频率加大, 如果视觉刺激面积增大则峰值振荡频率减小. 这一建模研究和生物学实验发现具有较高的一致性, 然而在他们的研究中仅采用了简化的随机神经元模型和简单的耦合结构.因此, 对依赖输入刺激信号的频率变化的伽马振荡机理的建模研究远不充分.

为了理解刺激引发变频率伽马振荡的生物学实验结果并揭示其动力学产生机理, 分别研究了简单刺激和视觉刺激调控的E/I 神经网络的伽马振荡动力学和具有功能柱结构的大规模复杂神经网络的伽马振荡动力学, 接下来对此进行简要阐述.

3.2.1 简单刺激调控下的变频伽马振荡动力学

采用3.1 节所介绍的IAF 神经元模型 (式(1)) 和基于电导的突触模型 (式(2)) , 构建了一个由简单刺激调控的全连接结构的兴奋性/抑制性 (E/I) 神经网络模型, 该E/I 神经网络的结构如图2 所示.

建模过程中的一个重要问题是如何将视觉刺激引入神经网络模型. 在视觉通路的信息处理中, 视网膜、外侧膝状体核 (LGN) 以及初级视觉皮层 (V1 区) 中的神经元在视野的有限区域内对外部刺激作出反应, 这个有限的区域被称为神经元的感受野 (receptive field, RF) , 又称为经典感受野 (classical receptive field, CRF) (Richard 1987). 在生物学实验中可以观察到, 在神经元感受野中的周围刺激对比度的增加会使得抑制性神经元的输入增加, 而兴奋性神经元的输入几乎不变; 中心刺激对比度的增加会使得兴奋性神经元的输入增加, 而抑制性神经元的输入几乎不变 (Jadi & Sejnowski 2014a) . 以此为依据, 将外部视觉刺激简单地映射为兴奋性神经元和抑制性神经元的输入电流, 即设置E 神经元的外部输入为S1和I 神经元的外部输入为S2, 通过调整输入差异|ΔS| = |S1-S2|对E/I 网络进行调控, 即分别使ΔS＜ 0 或者ΔS＞ 0, 来模拟生物学实验中的周围刺激对比度的增加或中心刺激对比度的增加.

图2简单刺激调控的E/I 神经网络. 红色和蓝色的圆分别表示E、I 神经元集群 (400 个兴奋性神经元和100 个抑制性神经元) , 红色定向线表示兴奋性连接, 蓝色定向线表示抑制性连接. w EE 、wII 、 w EI 和 w IE 分别是E 神经元连接到E 神经元、I 神经元连接到I 神经元、E 神经元连接到I神经元、I 神经元连接到E 神经元的突触权重. I Eext 和 I Iext 分别表示网络中E 神经元和I 神经元接收到的外部刺激输入 (Gu et al. 2021a)

调整神经突触的连接强度, 观察神经网络的同步动力学行为的涌现 (连接强度的调整主要依据E 和I 神经元的比例按照一定经验和规律进行). 可以发现, 在平衡的E/I 神经网络 (即ΔS= 0)中, 无论如何调整参数, 网络均表现为随机振荡模式 (见图3(a)) , 对应的神经元平均群体活动的功率谱图 (图3(d)) 只有多个局部高峰, 显示在该神经元的群体活动中没有主导频率; 而在具有输入差异的E/I 网络 (即ΔS＜ 0 或ΔS＞ 0) 中, 无论差异为正还是为负, 神经元网络的放电时刻斑图均可呈现明显的同步振荡行为 (见图3(b)和图3(c)) , 神经元平均群体活动的功率谱图(见图3(e)和图3(f)) 显示网络的峰值振荡频率处于伽马频带, 即刺激差异可诱发网络呈现不同频率的伽马振荡.

在研究网络伽马振荡的频率和强度与刺激差异的关系 (如图4)时, 发现在中心刺激对比度增加 (由增大S1、保持S2不变来实现) 和周围刺激对比度增加 (由增大S2、保持S1不变来实现)两种调节情形下, 网络振荡的频率和峰值功率 (强度) 均随着外部输入差异绝对值的增大而增大. 这一结果和现有的生物学实验观察结果 (Henrie et al. 2005, Ray & Maunsell 2010, Jia et al.2013b, Perry et al. 2015, Saleem et al. 2017) 一致.

进一步的研究为刺激差异导致伽马振荡频率增加的动力学机理 (如图5) . 在中心刺激对比度增加 (即增大E 神经元的输入、保持I 神经元的输入不变) 的情形下, E 神经元集群的平均放电率随着E 神经元的外部输入的增大而增大, 而E 神经元群的活动增强导致I 神经元群的兴奋性突触输入增加, 使它们更频繁地放电及出现更强的群体活动. 这种情况下明显是兴奋性神经元的活动支配着整个网络, 因此E/I 网络的振荡遵循PING 机理, 即网络的振荡频率取决于兴奋性神经元从抑制中恢复的持续时间 (Tiesinga & Sejnowski 2009) . 所以, 随着E 神经元外部输入的增大 (也就是网络外部输入差的增加) , E 神经元的平均放电率增大, 使得E/I 网络的振荡频率也随之增大. 在周围刺激对比度增加 (即增大I 神经元的输入、保持E 神经元的输入不变) 的情形下, 随着周围刺激对比度的增加也就是I 神经元外部输入的增大, I 神经元集群的放电率递增,E 神经元集群的放电率递减, 使得整个网络的活动主要由抑制性神经元集群支配, 导致了由ING 机理诱导的伽马振荡的产生 (Tiesinga & Sejnowski 2009) ; 而根据ING 机理, 网络的振荡频率由抑制性神经元的放电率决定, 因此E/I 网络的振荡频率随着I 神经元外部输入的增大 (也就是外部差异的增大) 而增大.

图3平衡和具有外部输入差异的E/I 神经网络的仿真结果.左列、中列、右列图分别为 S =0 (S1 = S2 = 2.5 μA) 、 S ＜0 (S1 = 2.5 μA, S2 = 3.1 μA) 和 S ＞0 (S1 = 3.1 μA, S2 = 2.5 μA) 的情况.(a) (b) (c)神经元的放电时刻斑图, 编号为0 ～ 100 的神经元是抑制性神经元, 编号为101 ～ 500的神经元是兴奋性神经元; (d) (e) (f)神经元平均群体活动的功率谱图(这里采用的是相对功率,即功率谱中每个频率分量的功率与所有频率分量的功率之和的比值) (Gu et al. 2021a)

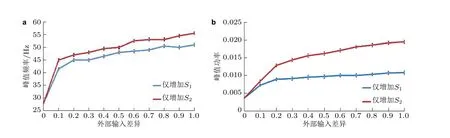
图4两种刺激调节方式下Gamma 振荡和E、I 神经元集群的外部输入差异之间的关系 (中心刺激对比度增加由增大S1、保持S2 不变来实现, 周围刺激对比度增加由增大S2、保持S1 不变来实现).(a) Gamma 振荡的频率随外部输入差异的增大而增大; (b) Gamma 振荡的峰值功率随外部输入差异的增大而增强 (Gu et al. 2021a)

图5 E/I 神经网络中 E 神经元集群和 I 神经元集群的平均放电率. (a) E 神经元具有不同输入时 E, I神经元集群的放电率变化; (b) I 神经元具有不同输入时 E, I 神经元集群的放电率变化 (Gu et al. 2021a)

由此, 可得出结论: 变频伽马振荡的产生是由于兴奋性和抑制性神经元集群的外部输入不同而导致E/I 网络的同步放电分别由ING 或PING 机理主导, 而无论是哪种机理主导, 其振荡频率均会随着外部输入差异的增大而增大. 之后对该E/I 神经网络简化模型的数学推导 (Gu et al.2021a) 也从理论上证实了E/I 网络伽马振荡的频率会随外部输入差的增大而增大.

最后对网络振荡强度与刺激差异的依赖性也作了动力学机理分析. 可以发现不存在刺激差异的时候网络中任意神经元的总突触电流在零值附近波动, 那么, 这种状态的网络中的神经元可以看作是彼此间没有突触连接的孤立神经元, 这种几乎孤立的神经元独立释放动作电位且无法引发伽马振荡和网络同步. 存在刺激差异的时候, 在S＞0 的情形下, 任意神经元的总突触电流为正 (如图6(a) 的红色线) , 这个正的总突触电流使得E/I 网络类似于一个兴奋性网络, 由于在短暂的突触延时下兴奋性网络很可能会同步, 且伽马振荡通常是在突触延时较短的局部神经回路中产生的, 因此较大的外部输入差异将引起较大的正的总突触电流, 从而导致网络产生较强的峰值功率, 即产生更强的伽马振荡或网络同步; 在S＜0 的情形下, 任意神经元的总突触电流为负(如图6(b) 的红色线) , 使得E/I 网络类似于一个更易于同步的抑制性网络, 因此, E 神经元和I神经元之间的外部刺激输入差异越大, 任意神经元的负的总突触电流就越大, 因此平均总突触电流 (绝对值) 也越大, 从而导致越来越高的峰值功率, 即产生更强的伽马振荡或网络同步. 因此,不管是哪种调节情形, 任意神经元的总突触电流的绝对值均随着外部输入差异的增大而增大, 整个E/I 网络的同步性是不断增强的, 从而使得网络振荡的峰值功率也就是伽马振荡的强度随刺激差异的增大而增大.

图6 E/I 神经网络中任意一个神经元的突触电流: (a) S ＞0 的情形 (E 神经元和I 神经元的输入分别为 3.5 μA 和 2.5 μA) ; (b) S ＜0 的情形 (E 神经元和I 神经元的输入分别为2.5 μA 和3.5 μA) .图中黑色线表示该神经元接收到的兴奋性突触电流, 蓝色线表示该神经元接收到的抑制性突触电流, 红色线表示总突触电流, 为前二者之和. 网络平均总突触电流和伽马振荡的峰值功率之间的关系: (c) S ＞0 的情形 (E 神经元和I 神经元的输入分别为 3.5 μA 和 2.5 μA) ; (d) S ＜0 的情形 (E 神经元和I 神经元的输入分别为2.5 μA 和3.5 μA) (Gu et al. 2021a)

3.2.2 视觉刺激调控的E/I 神经网络模型及其伽马振荡动力学

为了完整地模拟生物实验现象中伽马振荡频率对光栅刺激的灰度对比度的依赖性, 考虑真实刺激的特征和V1 区神经元的特点, 建立了基于高斯差分 (difference of Gaussians, DOG) 感受野的光栅视觉刺激模型.

视觉神经元的感受野分为两种类型, 分别是ON-Center 型感受野和OFF-Center 型感受野(见图7 左下和左上) . ON-Center 型感受野由环形周围抑制区域围绕着圆形中央兴奋区域, 当刺激信号位于感受野中心时, 神经元放电最强烈; 当刺激向感受野中心外围移动时, 神经元放电开始减弱. 相反, OFF-Center 型感受野由环形周围兴奋区域围绕着中央抑制区域, 神经元放电模式与 ON-Center 型感受野正相反. 采用DOG 感受野模型来模拟神经网络中E 神经元和I 神经元的感受野 (Rodieck 1965, 1975) , 其空间结构可通过式 (3) 表示 (Dayan & Abbott 2001)

式中第一个高斯函数描述了强度较大但范围较窄的中心区, 另一个高斯函数描述了强度较弱但范围较大的周围区. 感受野的中心设置在点 (a,b) 处,σcen决定了感受野中心区域的大小,σsur决定了感受野周边区域的大小且大于中心区域,B控制着中心区和周边区的平衡,±分别表示ONCenter 型感受野 (对应于E 神经元) 和OFF-Center 型感受野 (对应于I 神经元) .

图7视觉刺激调控的E/I 神经网络的结构, 左侧示意图分别表示E 神经元 (下方) 和I 神经元 (上方)的感受野的空间结构. 叠加在光栅刺激 (右上方) 上的感受野显示为两个椭圆区域, 黑色的表示OFF 区域, 白色的表示ON 区域 (Gu et al. 2019)

由于生物学实验中通常采用真实的光栅作为视觉刺激, 特意建立了明暗条纹相间的光栅作为网络的外部刺激模型. 在该网络中, 假设E 神经元对光栅刺激的亮条纹敏感, 而I 神经元对光栅刺激的暗条纹敏感, 则将光栅刺激的亮条纹设置为与E 神经元感受野的ON 区域重叠, 将暗条纹设置为与I 神经元感受野的OFF 区域重叠, 如图7 所示. 假设光栅刺激的明暗条纹之间具有不同的灰度值, 它们之间的灰度值差异模拟了E/I 网络外部视觉刺激的灰度对比度输入. 因此,采用G1表示与E 神经元对应的亮条纹的灰度值, 采用G2表示与I 神经元对应的暗条纹的灰度值, 那么E/I 网络的灰度对比度G为

由此构建了由光栅视觉刺激调控的兴奋性/抑制性 (E/I) 神经网络模型 (图7) . 依据光栅刺激的灰度对比度特征建立网络的输入信号, 以更接近实际生物神经系统的方式模拟V1 区的简单神经回路. E/I 神经网络中的兴奋性神经元 (E 神经元) 和抑制性神经元 (I 神经元) 的动态均由

3.1 节所介绍的IAF 神经元模型 (式(1)) 和基于电导的突触模型 (式(2)) 来描述.

调整突触连接强度可以使得神经网络的放电行为尽可能同步. 图8 显示了网络的放电时刻斑图、神经元的平均群体活动的功率谱图, 可以发现: 在光栅条纹灰度对比度为零时, 无论如何调整参数, E/I 神经网络的放电斑图均呈现出杂乱无章的随机性 (图8(a)) , 神经元平均群体活动的功率谱没有明显峰值 (图8(d)) , 表明网络不产生伽马振荡. 然后通过增加光栅刺激的灰度对比度 (即增加光栅刺激明暗条纹的灰度值G1和G2之间的差) 对网络进行调节并观察网络是否能够产生伽马振荡以及由灰度对比度引发的伽马振荡的频率和功率的变化. 采用以下两种调节方式模拟实验中的光栅刺激灰度对比度增加: (1) 减小暗条纹的灰度值G2, 且保持亮条纹的灰度值G1不变; (2) 同时增大亮条纹的灰度值G1和减小暗条纹的灰度值G2. 这两种调节方式下的仿真结果都表明, 当光栅视觉刺激具有灰度对比差异时, 网络能够产生明显的同步放电节律 (图8(b)和图8(c)) , 此时神经元平均群体活动的功率谱具有明显的峰值且峰值频率处于伽马频带(图8(e)和图8(f)) , 且采用上述两种灰度对比度调节方式均可发现网络伽马振荡的频率和峰值功率随着灰度对比度的增大而增大 (为简略起见, 仅给出第二种调节方式下的伽马振荡的频率和峰值功率变化, 如图9) , 这一仿真结果和生物学实验结果 (Henrie et al. 2005, Ray & Maunsell 2010, Jia et al. 2013b, Perry et al. 2015, Saleem et al. 2017) 一致.

3.2.3 具有立柱结构的大规模复杂E/I 神经网络及其伽马振荡动力学

神经科学领域普遍认为大脑皮层的神经网络是以功能柱结构为基本单元构成的 (Mountcastle 1997, Petersen & Sakmann 2013) . 单个功能柱结构可以在内部处理和存储信息, 并且在各功能柱结构之间发送和接收各种信息. 由于初级视觉皮层 (V1 区) 的伽马振荡和视觉刺激的特征 (如图像灰度对比度) 关系密切, 因此本小节以初级视觉皮层的功能柱神经网络结构为基础,建立一个具有多层立柱结构的大规模复杂E/I 神经网络模型来进一步研究依赖于刺激的变频伽马振荡. V1 区包含多种类型的神经元, 其神经网络结构比较复杂, 从横向看分为 6 层, 从纵向看由许多相对独立的功能柱组成. 这些功能柱的每一层的局部神经回路结构都有所不同, 层与层之间有突触连接, 柱与柱之间也有突触连接. 根据初级视觉皮层 V1 区的网络结构以及从视网膜通过外侧膝状体核 (LGN) 到 V1 区的视觉通路 (Bear & Connors 2004) , Kang 等 (2010) 提出了一个简化的 V1 区模型. 根据这一简化的 V1 区模型, 首先建立一个立柱结构模拟功能柱 (图10(a)) ,然后以立柱结构为单位进行建模, 建立了一个具有10 个立柱结构的、共计10 000 个神经元的大规模复杂神经网络模型 (图10(b)和图10(c)) , 网络模型中仍然采用3.1 节所介绍的IAF 神经元模型和基于电导的突触电流模型.

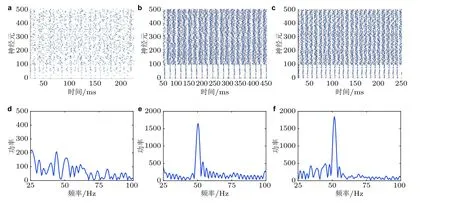
图8光栅无灰度对比度的平衡E/I 神经网络 (左列图) 、第一种调节方式下光栅具有40%灰度对比度的E/I 神经网络 (中列图) 、第二种调节方式下光栅具有60%灰度对比度的E/I 神经网络 (右列图) 的仿真结果. (a) (b) (c) 神经元的放电时刻斑图, 标号0 ～ 100 的神经元是抑制性神经元,标号101 ～ 500 的神经元是兴奋性神经元; (d) (e) (f) 神经元平均群体活动的功率谱图(Gu et al.2019)

在这么一个大规模的复杂神经网络模型里, 神经计算的工作量将非常之大, 为此设计了基于CUDA 并行技术结合突触优化计算的并行仿真算法, 实现了该网络的模拟仿真. 算法的基本思想是: 在单位仿真步长内, 每个神经元的状态计算主要包含两个步骤: (1) 总突触电流的计算,(2) 膜电位的计算. 采用基于CUDA 并行技术的神经元级并行策略, 将上述两步骤的计算任务分别映射到GPU 的单个处理单元上, 即给网络中的每个神经元分配一条线程, 通过执行所有线程的并行计算完成所有神经元的状态计算. 在计算神经元的突触输入电流时, 如果采用传统的串行算法, 神经网络的电导系数和突触电流的计算量会随着神经元的数量平方增长, 为此, 提出一种基于虚拟突触的突触电流优化计算方法 (Peng et al. 2018, Wang et al. 2020) , 将电导系数提取了一个时间序列预先存储, 具体计算的时候再根据突触延时从中取用, 极大地降低了突触电流的计算量, 提高了大规模神经网络的仿真效率.

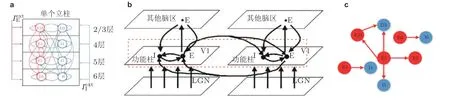
图10具有立柱结构的大规模复杂E/I 神经网络. (a) 单个立柱中层内和层间神经元之间的连接; (b)V1 区的简化模型 (Kang et al. 2010) , 其中 E 表示兴奋性神经元集群, I 表示抑制性神经元集群,箭头表示神经信号投射方向, 图中只画出 2 个功能柱; (c) 立柱和立柱之间神经元的连接结构 (Gu et al. 2021b)

利用上述神经计算方法, 研究了外部刺激不同时该大规模复杂E/I 神经网络的伽马同步振荡现象及其振荡频率特性, 结果如图11. 无论外部刺激差异大于零还是小于零, 通过调整突触权值等参数, 该网络均可呈现节律同步放电行为 (图11(a)和图11(b)) . 对神经元网络平均群体活动做功率谱分析 (图11(c)) , 发现网络的峰值振荡频率均在伽马频带, 且存在快、慢两个峰值频率. 进一步可以发现在中心刺激对比度增加 (由增大S1、保持S2不变来实现) 和周围刺激对比度增加 (由增大S2、保持S1不变来实现) 两种调节方式下该大规模神经网络的伽马振荡频率均随着外部刺激差异的增大而增大 (图12) , 再次验证了生物实验结果 (Henrie et al. 2005, Ray &Maunsell 2010, Jia et al. 2013b, Perry et al. 2015, Saleem et al. 2017) .

3.3 神经系统伽马振荡的认知功能研究

虽然很多生物学实验依据已经表明伽马振荡是大脑多种认知功能的内在基础, 但是采用建模方法对伽马振荡的认知功能的动力学机理进行研究尚处于初步阶段. 目前的主要工作只是利用一些简化的模型 (即未充分考虑相关脑区网络结构和神经元特点的模型) , 对伽马振荡的认知作用机理进行假设验证 (Mcclelland & Rumelhard 1986, Fries 2005, Fries et al. 2007, Brette 2007, Borgers & Kopell 2008, Masuda 2009, Neymotin et al. 2011, Wildie & Shanahan 2012) . 例如, Fries 等提出了上下游神经元集群基于伽马振荡进行信号传递的思想, 如果上游和下游神经元集群都处于高频同步振荡模式, 同时振荡的相位差所对应的时间正好是上游神经元到下游神经元的突触延时, 则调制在伽马振荡中的上游神经元的信号能被有效地传递到下游神经元集群中 (Fries 2005, Fries et al. 2007) . 依据此思想, Borgers 和 Kopell (2008) 提出了对于驱动下游神经元放电的效率而言, 强的振荡性信号比弱的振荡性信号具有优势, 意味着在强的伽马振荡中的信号能克服其他没有很强振荡性的信号的干扰, 可靠地传递到另一群由兴奋性-抑制性神经元构成的神经元集群中. Masuda (2009) 依据 Fries 的思想, 提出了基于放电率集群编码的信号如何被选择性地传递到下一神经元集群的思想. 假设上游有两个神经元集群 A 和 B, 下游有一个神经元集群 C, A 和 B 都通过突触连接到 C, 三个神经元集群的放电都呈现高频同步振荡形式, 假设A 和C 同相位, 而 B 和 C 反相位, 则调制在 A 中的信号能被选择性地传递到 C, 而 B 中信号则被过滤掉. 这种现象意味着伽马振荡可能在选择性接收输入信号的认知功能中起到了重要的作用. Wildie 和Shanahan (2012) 提出的模型也能依据高频同步振荡选择性地进行刺激的传递, 而且他们还研究了突触参数对这种高频同步振荡认知功能的影响, 并找出了最优参数空间.以上的绝大多数研究都在假设伽马振荡已存在的前提下研究其认知机制. 在 Borgers 等 (2008)提出的模型中, 高频同步振荡是网络内生的, 而不是假设的, 外部刺激能基于此高频同步振荡展开竞争. 还有一些研究 (Fries et al. 2007, Onslow et al. 2014) 讨论了高频和低频振荡两种振荡跨频率耦合 (cross-frequency coupling) 的认知机制.

图11具有多层立柱结构的大规模复杂E/I 神经网络产生的 Gamma 振荡. (a) 当外部输入为 S1 = 0.3、S2 = 0 时每层神经元的放电时刻斑图; (b) 当外部输入为 S1 = 0, S2 = 0.3 时每层神经元的放电时刻斑图; 图(a)(b)中红色点代表抑制性神经元的放电, 蓝色点代表兴奋性神经元的放电;(c) 分别对应于 (a) 和 (b) 的神经元群体活动的功率谱图(Gu et al. 2021b)

图12具有多层立柱结构的大规模复杂E/I 神经网络中Gamma 振荡的振荡频率对输入差异的依赖性.红色和蓝色曲线分别代表中心刺激对比度增加 (增大S1、保持S2 为0) 和周围刺激对比度增加(增大S2、保持S1 为0) 的调节情形 (Gu et al. 2021b)

上述对伽马振荡认知功能的建模研究都是针对固定的振荡频率的研究, 而依赖于刺激的伽马振荡的频率随刺激特征的变化而变化, 其认知功能有待进一步的建模研究揭示. 依据神经科学中著名的侧抑制 (Valley & Firestein 2008, Kim & Bertalmio 2015) 思想, 揭示了E/I 神经网络由同步抑制导致的全局放电率对比度增强的动力学机制 (此机制不受伽马振荡频率变化的影响) ,并提出神经信息效能指标来衡量放电率对比度增强对于提高神经系统信息传输能力的效果.

3.3.1 循环侧抑制网络的放电率对比度增强

通常认为神经系统是以神经元输出的放电率对刺激输入的信息进行编码 (Dayan & Abbott 2001, Huxter et al. 2003, Panzeri et al. 2010) . 如果系统中神经元的输入差异很小, 为了使刺激信息能够可靠地编码和传递, 神经系统应输出较大差异的放电率 (即放电率对比度增强) 才能清晰地传递信息. 这种观点可由关于视网膜神经节细胞的生物实验 (Bear & Connors 2004) 所验证. 因此, 神经元放电率对比度的增强可能是神经系统的一个重要功能 (Han et al. 2018) .

受神经科学中侧抑制 (Valley & Firestein 2008, Kim & Bertalmio 2015) 概念的启发, 提出了基于循环侧抑制的神经网络放电率对比度增强机制. 在侧抑制概念里, 对于如图13(a) 所示的前馈神经网络模型 (Bear & Connors, 2004) , 相邻兴奋性神经元输出的放电尖峰个数差异 (一般认为, 外部刺激编码在兴奋性神经元的输出放电率里) 在接收了侧面抑制性神经元的输入后产生了明显的增加 (比如, 神经元C 和D 的输出放电率本是15 和30, 在受到侧抑制后变成0 和20) ,即相邻兴奋性神经元的放电率对比度受到侧抑制后发生增强. 受侧抑制机制的启示, 在更一般的循环神经网络模型里去检验抑制性神经元的输入对兴奋性神经元的输出放电率的影响, 建立了一个侧抑制循环E/I 神经网络模型, 其结构如图13(b) 所示.在该循环网络中, 不同于前向神经网络, 每个兴奋性神经元的输出均会通过侧面的抑制性神经元再次输入到兴奋性神经元本身, 构成循环网络结构. 这里, 神经元模型仍然采用3.1 节所述的IAF 神经元模型和基于电导的突触电流模型, 只是在用参数设置神经元兴奋和抑制类型时, 将抑制性神经元设置为具有快速放电特性的“fast-spiking”中间神经元.

图13(a) 前馈神经网络结构 (Bear & Connors, 2004) . 标有字母A-G 的圆圈表示兴奋性神经元, 小黑点表示抑制性神经元; (b) 侧抑制循环神经网络结构. 标有字母a-d 的抑制性神经元收到来自侧向兴奋性神经元 (标有字母A-E) 的反馈, 并侧向抑制相邻的兴奋性神经元 (Han et al. 2018)

为了判断兴奋性神经元的放电率是否增强, 通过分离出兴奋性神经元 (即断开其与抑制性神经元的连接) 、与循环神经网络 (图13(b)) 结构中兴奋性神经元的放电率做了对比研究 (见表1) ,发现由于来自邻近抑制性神经元的反馈抑制输入, 相邻兴奋性神经元 (比如B 和C、C 和D) 的(归一化) 放电率对比度增强.

表1 侧循环抑制引起的局部放电率对比度增强 (Han et al. 2018)

相邻的兴奋性神经元接收同一个抑制性神经元的突触输入, 但为何其放电率对比度却有所提高？可以发现其潜在的动力学机理源于突触电流的电压依赖性. 具体来说, 突触电流取决于突触后神经元的膜电位, 以及突触的离子通道开放水平和突触的连接强度 (见3.1 节式(2)) . 以兴奋性神经元“A”和“B”为例, 模拟出神经元放电过程中的膜电位和突触电流变化情况, 如图14 所示.如果兴奋性神经元“B”具有更高的放电概率, 那么它对神经元“A”的抑制性电流会比神经元“A”对它的抑制性电流更大 (如图14(d)(e) 所示) , 相应地就会有更高的概率去抑制神经元“A”的放电, 从而进一步增大了神经元“B”和神经元“A”的放电率对比差异.

而当设置循环神经网络的所有抑制性神经元全连接且同步放电的时候, 图13(b)所示的循环网络结构就成为图15(a)所示的结构, 而由于抑制性神经元集群已经同步, 则相当于网络中仅有一个抑制性神经元, 因此可以等效为图15(b)所示的简单网络结构. 通过对该循环E/I 神经网络的仿真可得到如图15(c)所示的同步放电斑图, 可以明显地发现, 网络中抑制性神经元的放电是同步的, 但兴奋性神经元的放电不同步, 也就是说, 兴奋性神经元的放电会携带有外部输入的信息而不会同步. 再次通过分离出兴奋性神经元 (断开其与抑制性神经元的连接) 、与图15(a)或(b)网络结构中兴奋性神经元的放电率做了对比研究, 可以发现网络中任意兴奋性神经元之间的 (归一化) 放电率差异都增大了 (比如表2 中的神经元“A”和“E”) . 比较图15(a)或(b)和图13(b)可以发现, 图15(a)或(b)中的同步抑制性神经元集群对所有兴奋性神经元都有抑制作用, 而图13(b)中的每个抑制性神经元仅对相邻的兴奋性神经元起侧向抑制作用. 因此, 可以得出结论, 由于同步的抑制性神经元起到了全局抑制的作用, 图15(a)或(b)中的兴奋性神经元的放电率对比度可以得到整体增强, 即在循环结构的E/I 神经网络模型中, 抑制性神经元集群的同步可以引起网络中兴奋性神经元的放电率对比度全局增强 (而此时网络呈现伽马同步振荡行为) .

表2 抑制性同步引起全局放电率对比度增强 (Han et al. 2018)

图14在兴奋性神经元“B”放电引起抑制性神经元“a”放电的情况下, 兴奋性神经元“A”和“B”的膜电位和接收的抑制性突触电流. (a) 神经元“B” “a”和“A”的放电, 黑点代表相应神经元的放电, 其中“A”未达到阈值电位而没有放电; (b) 神经元“A”的膜电位; (c) 神经元“B”的膜电位; (d) 神经元“A”接收的抑制性突触电流; (e) 神经元“B”接收的抑制性突触电流 (Han et al. 2018)

之后, 在全局耦合的复杂E/I 神经网络模型 (如图16) 中验证抑制性同步是否有类似增强放电率对比度的作用, 即研究在网络产生同步 (即伽马振荡) 时E/I 神经网络的放电率对比度变化情况. 这类E/I 神经网络中抑制性神经元的同步性已得到广泛验证 (Tiesinga & Sejnowski 2009,Wang et al. 2011, Buzśaki & Wang 2012) . 通过对该复杂E/I 神经网络进行适当的参数设置及仿真, 可得到如图17(a)所示的同步放电斑图, 从中可以发现, 抑制性神经元是同步放电的, 兴奋性神经元是弱同步放电 (即在同步的每个周期中只有一小部分兴奋性神经元放电) , 整个网络呈现伽马振荡. 如果从该E/I 网络中取出抑制性神经元而仅保留兴奋性神经元, 那么即使外部刺激输入的标准偏差 (表征刺激输入的差异) 较大, 兴奋性神经元的归一化放电率的标准偏差也很小(图17(b)方形线) , 这意味着在没有抑制性神经元的网络中, 兴奋性神经元的放电率对比度较小; 当网络中包含抑制性神经元时, 兴奋性神经元的归一化放电率的标准偏差 (表征兴奋性神经元的放电率对比度) 增大 (图17(b)中星形线) . 图17(b)也显示了放电率对比度的增强倍数(见点线, 为星形线和方形线之比) , 可见该比率大于1 (特别是当外部输入的差异较大时) , 表明在同步抑制的作用下, E/I 神经网络的放电率对比度相较纯兴奋性神经元网络提高. 并且, 在网络的部分同步 (弱同步) 情形 (图17(c)) 下, E/I 神经网络的全局放电率对比度增强现象更为显著 (放电率对比度的增强倍数大于4) (图17(d)) , 提示了E/I 神经网络部分同步状态可能更加有利于放电率对比度的增强, 从而对提高神经信息传输效率更有意义.

图15抑制性神经元同步放电的循环E/I 神经网络及其放电模式. (a) 由5 个兴奋性神经元和5 个全连接的同步抑制性神经元 (在虚线椭圆中) 组成的简单E/I 网络; (b) 与 (a) 等效的E/I 网络; (c)图(a) 中E/I 神经网络的同步放电模式, 索引为1 ～ 5 的神经元表示兴奋性神经元 “A”-“E”, 索引为6 ～ 10 的神经元表示抑制性神经元 (Han et al. 2018)

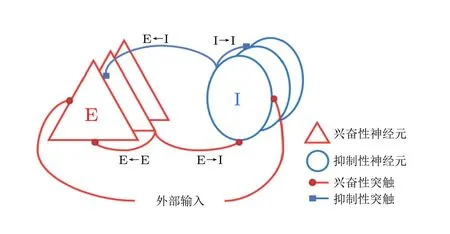
图16全局连接复杂E/I 神经网络的结构 (Han et al. 2018)

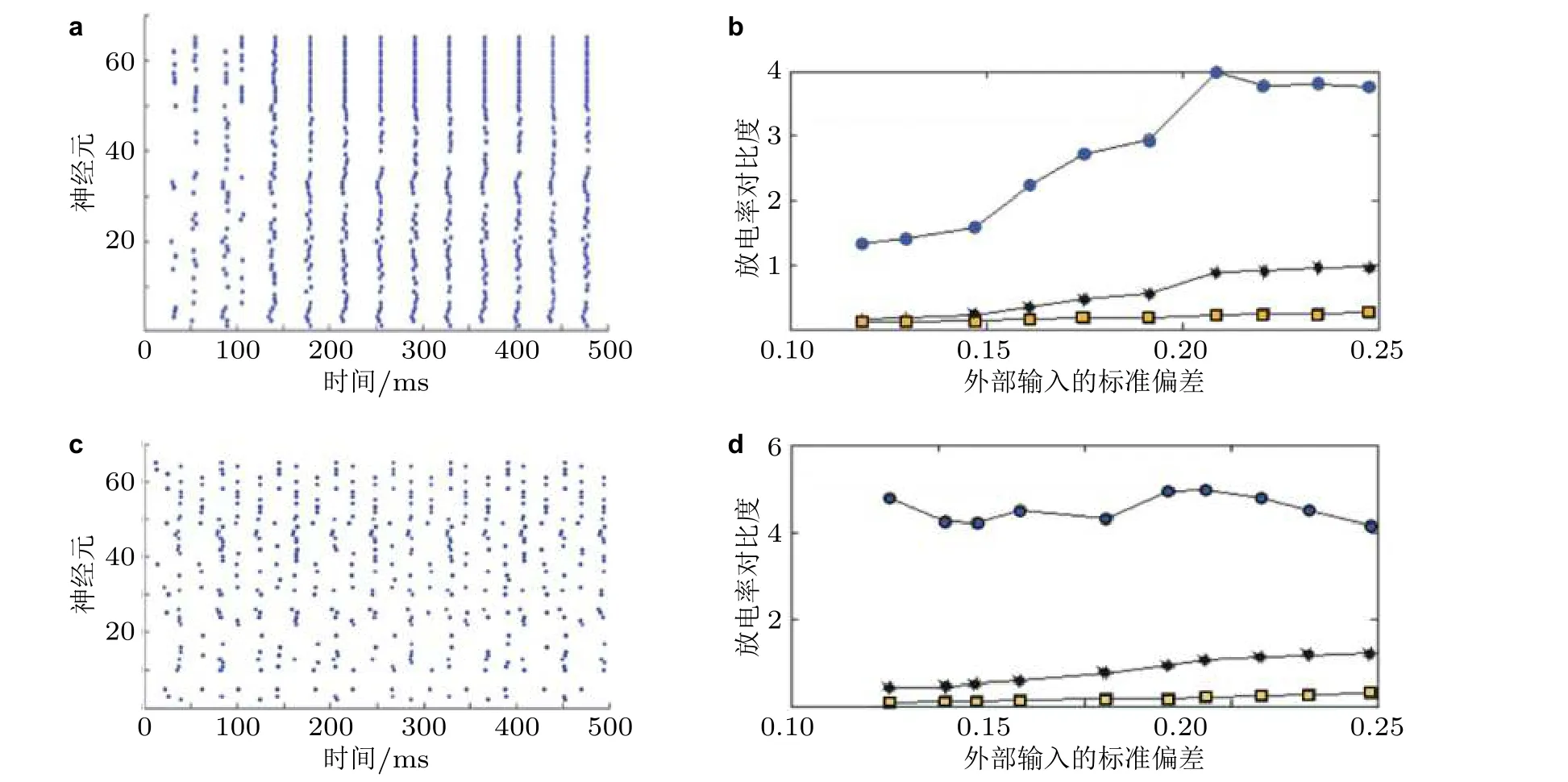
图17(a) (c) E/I 神经网络的同步和部分同步状态, N = 65, 其中神经元1 ～ 50 是兴奋性神经元, 神经元51 ～ 65 是抑制性神经元; (b) (d) E/I 神经网络的放电率对比度, 图中方形线表示纯兴奋性神经元 (断开抑制性连接) 的归一化放电率的标准偏差, 星形线表示全局耦合的E/I 神经网络中的兴奋性神经元的归一化放电率的标准偏差, 点线表示E/I 神经网络和纯兴奋性神经元网络的放电率对比度增强倍数 (Han et al. 2018)

上述建模研究揭示了抑制性神经元同步可作为全局抑制增强E/I 神经网络中兴奋性神经元的全局放电率对比度的动力学机理, 并指出抑制性神经元的完全同步 (所有抑制性神经元在同步的每个周期都同步放电) 和部分同步 (仅一部分抑制性神经元在每个同步周期同步放电) 都可以起到这样的全局抑制作用. 由于外部刺激信息编码在兴奋性神经元的输出放电率中, 放电率对比差异的增强表明提高了网络的输入与输出之间的互信息, 从而可提高神经信息传输效率. 值得注意的是, 在上述研究中, 并不需要同步振荡的频率固定, 也就是说, E/I 网络中的伽马同步振荡频率改变并不影响上述结论的成立.

3.3.2 神经网络信息传输效能的建模研究

3.3.1 节指出神经系统利用同步将输出放电率差异增大, 由此可提高神经信息传输效果. 这一小节建立了更一般的随机E/I 神经网络, 即网络具有随机连接结构、神经元的输入都加入随机白噪声 (如图18(a)所示) , 定义神经信息传输效能指标, 进一步将放电率增强现象对神经信息传导的作用利用信息熵来量化描述 (Han et al. 2020) .

图18(a) 随机E/I 网络结构. 该网络由一个大小为 N e 的兴奋性神经元集群和一个大小为 Ni 的抑制性神经元集群组成. 网络中任意神经元连接到其他神经元的概率为 ρ . (b) 该网络产生的Gamma 同步振荡 (Han et al. 2020)

该E/I 神经网络中的兴奋性神经元 (E 神经元) 和抑制性神经元 (I 神经元) 的动力学仍由IAF 模型 (3.1 节式(1)) 来描述. 突触电流为:

该随机网络仍然可通过调整突触连接强度等参数呈现伽马同步振荡, 如图18(b)所示.

在神经元输入无噪声的情形下, 可以将纯兴奋性 (E) 神经元网络 (在该E/I 网络中切断兴奋性神经元与抑制性神经元的联系) 的放电率对比度和该E/I 网络中兴奋性神经元的放电率对比度进行可视化处理, 即将神经元的输出放电率线性转化为图像的灰度值, 由图像灰度值的差异可直观地观察到放电率对比度的变化情况 (见图19) . 从图中可明显观察到, E/I 神经网络的放电率对比度相较E 神经元网络明显增强. 神经元输入有噪声的情形也类似. 对于随机E/I 网络的研究结果再次验证了3.3.1 节中E/I 神经网络的同步可增强兴奋性神经元放电率对比度的结论.

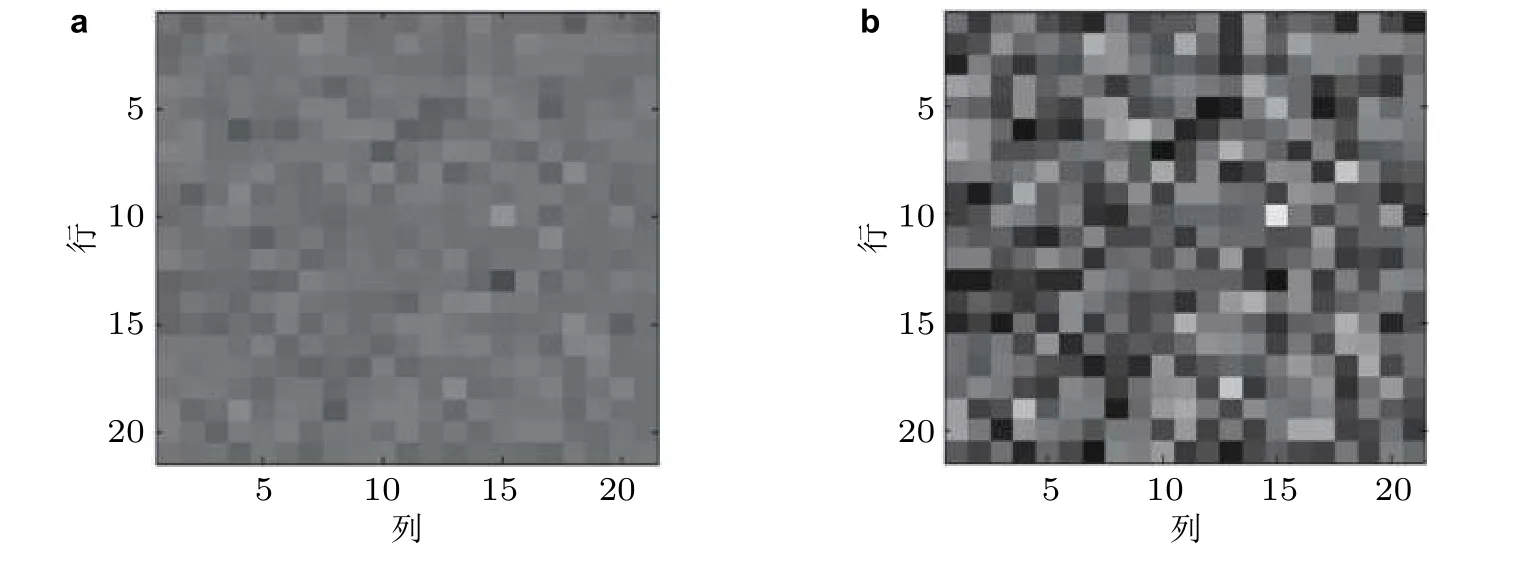
图19神经元输入无噪声情形下E/I 神经网络的放电率对比度增强. (a) 纯兴奋性神经元网络里400 个兴奋性神经元的放电率对比度可视化图像; (b) E/I 神经网络中400 个兴奋性神经元的放电率对比度可视化图像 (Han et al. 2020)

那么这种输出放电率的增强对于神经信息传输有何作用？从神经系统接受刺激到编码为输出放电率的过程中, 尖峰放电个数可能因为编码时间有限而产生输出重叠 (即本来神经元放电率不同, 但因编码时间有限而导致统计出的输出放电率相同) , 噪声干扰也可能会使得不同的刺激编码为相同的输出放电率, 这样均会使得神经信息传输能力降低. 而如果放电率输出差异增大, 则会减小放电输出重叠和噪声干扰的影响, 从而提高神经信息传输效率. 由此可见, 具有同步振荡的E/I 网络是有助于提高神经信息传输能力的.

编码在神经元中的信息通过神经系统逐层传输, 可以期望在信息通过带噪声的神经系统时只有很小的信息损失和能量消耗, 因此当神经系统以放电率编码信息时 (Moujahid et al. 2011,Kostal & Lansky 2013, Sengupta et al. 2014) , 也应该考虑能量消耗 (Wang et al. 2017, Zhu et al.2018) . 一个优化的神经系统应以更少的能量消耗来承载更多的信息 (Han et al. 2017) , 在此将能量消耗简单地由神经元发放电脉冲的频率来表示, 因此信息效能为

式中SI为互信息,FS为神经元的电脉冲发放频率. 为了比较E/I 网络与纯兴奋性E 神经元网络的信息传输效果, 定义信息传输效能比为

式中IE为E/I 网络的信息传输效能,IS为相应的纯E 神经元网络的信息传输效能,IC大于1 则表示神经信息传输效能提高.

我们模拟出神经信息传输效能指标IC与抑制性耦合强度、兴奋性耦合强度和外部刺激的标准差的关系, 如图20 所示. 当对兴奋性神经元的抑制强度降低即gIE降低时,IC下降 (见图20 实线) , 当抑制强度过弱时,IC甚至小于1, 这表明对兴奋性神经元无抑制的E/I 网络的信息传输效能比孤立的E 神经元群体更差. 这是因为无抑制时, 兴奋性突触电流 (对每个神经元来说都大致相同) 甚至可以使输入的对比度均质化, 因此, 增强抑制性是提高信息传输效能的重要手段. 图20还显示, 当从兴奋性神经元到抑制性神经元的突触强度gEI降低时,IC也下降 (见图20 虚线) , 这意味着从兴奋性神经元到抑制性神经元的输入对于信息传递的高效能也是必要的, 因此, E/I 网络中突触抑制和兴奋是共同作用来提高信息传输效能的. 而E/I 网络对于较大范围变化的外界刺激均有显著的信息传输效能增大 (见图20 点划线) , 只是随着差异增大其信息传输能力递减,而这也符合生物神经系统信息处理的一般认识 (当外界输入刺激差别较大时, 神经系统不需要通过增强放电率对比度即可有效传输信息) . 总地来说,IC在较大范围内均大于1, 说明E/I 网络的信息传输效能普遍高于孤立的兴奋性神经元网络, 即E/I 网络中的伽马同步振荡可增强神经系统信息传输效能.

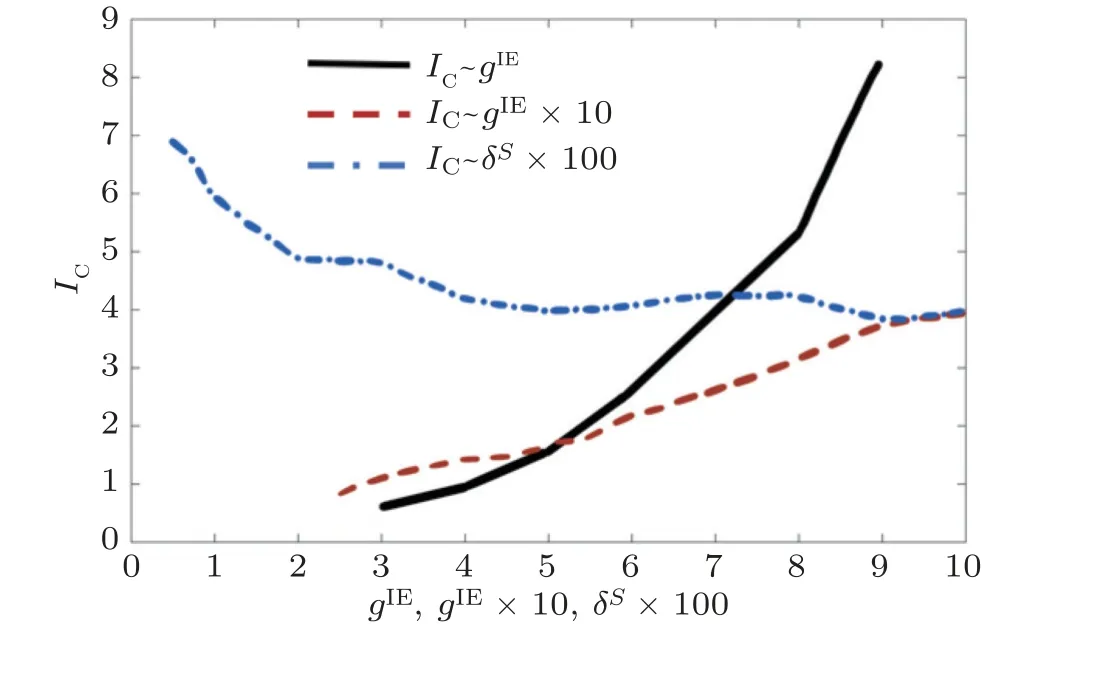
图20信息编码效能指标 IC 与以下参数的关系: 从抑制性神经元到兴奋性神经元的突触强度 g IE , 从兴奋性神经元到抑制性神经元的突触强度 g EI , 外部刺激的标准差 δs (Han et al. 2020)

4 总结与展望

生物学实验研究表明神经振荡对大脑的信息处理具有重要的作用, 尤其是高频同步伽马振荡 (30 ～ 90 Hz) 被认为与大脑的认知过程密切相关. 脑电中的高频伽马振荡的生理学研究结果多是在刺激信号固定的情况下发现的, 振荡的频率也是固定的, 但是神经生物学实验进一步发现各种特征的刺激信号如图像对比度信号、图像声音混合信号、运动视觉信号等刺激能够产生不同频率的伽马振荡, 而这种变频率的伽马同步振荡的产生机理及其潜在的认知功能至今未明. 依据在视觉V1 区的生物实验发现, 通过动力学建模和分析的途径去研究视觉刺激 (主要是图像对比度信号) 引起变频率伽马振荡的动力学机理及其认知功能的动力学机制, 即考虑真实生物神经系统的网络结构特点、神经元的特点以及真实刺激的实际特征, 建立E/I 神经网络动力学模型及输入信号模型, 研究刺激如何与网络的非线性动力学特性相互作用形成伽马同步振荡并调控伽马振荡的特性 (振荡频率和振荡强度) , 并在此基础上进一步利用动力学建模的方法探索该同步振荡的认知功能, 提出了E/I 神经网络利用抑制性同步增强网络全局放电率对比度的认知机制, 并利用信息熵工具量化全局放电率对比度增强对提高神经信息传输效能的作用.

研究工作基于神经系统伽马振荡的生物学实验结果, 综合利用神经动力学理论、数值仿真方法和信息论等, 研究大脑认知功能的动力学机制, 有助于理解神经系统同步振荡的内在动力学机理及认知功能的实现机制, 可为认知活动的脑机理提供借鉴, 也将为类脑智能的研究奠定基础.

然而, 研究工作仅依据视觉区依赖于刺激的变频率伽马振荡的生物实验现象做了建模研究,还有大量与神经振荡有关的生物实验现象有待通过建模研究来解释并揭示大脑认知原理, 在此过程中需要发展新的神经动力学建模理论和方法. 未来对于大脑认知功能的动力学研究, 还将围绕神经振荡展开, 大致分为两个思路: (1) 依据生物实验现象, 建立更加符合生物特征和实验现象的神经网络模型, 研究神经振荡原理和规律, 解释实验现象, 发展相关理论和方法; (2) 根据神经振荡的特征提出认知机制假说, 利用模型加以验证, 并力图寻求生物实验或实际应用的支持,以提出关于神经振荡的新的、完善的认知机制以及相关类脑机制. 对于大脑认知功能的探索是长期而艰巨的任务, 神经动力学将在解释生物实验现象和发展类脑机制的研究中发挥重要作用,相关成果对于推动认知神经科学、非线性动力学以及类脑智能的发展具有重要意义.

致 谢 国家自然科学基金 (11972115, 11932003, 12072021, 12102014) 资助项目.