水平电场下界面波的Hamilton 原理与多尺度建模

王 展

中国科学院力学研究所，北京 100190

中国科学院大学工程科学学院，北京 100049

1 引 言

现代电流体界面力学发轫于20 世纪六十年代, 美国的Melcher (1963)与英国的Taylor(1964)是该领域的开创者. Taylor 的出发点是研究水滴在强电场(如雷电)下的崩解, 随后他将问题抽象成垂直作用于导电液体自由表面的电场对系统稳定性的影响, 由此发现了“Taylor 锥”这一重要的物理现象. 垂直电场令导电流体失稳这一发现在后来的静电喷雾技术中发挥了重要作用, 被广泛应用于涂层工艺、冷却系统、微流控等工业领域. 与之相反, Melcher 则更关注平行于电介质流体间界面的电场对系统稳定性的影响(Melcher 1968). 在无黏假设之下, 水平电场为界面上的线性波贡献色散效应, 故可延缓液膜断裂的形成, 甚至抑制Rayleigh-Taylor 不稳定性(Barannyk 2015, Guan 2022).

近二三十年来, 对电场下无黏液膜自由表面波/界面波的研究, 无论是基于对多尺度约化模型的理论分析还是对原始Euler 方程的直接数值模拟, 都越来越聚焦于界面波动的非线性特征.例如, 电场作用下液膜界面的触壁奇异性(即形变界面触碰到槽道上下壁)(Barannyk 2015)、电场作用下的Rayleigh-Taylor 不稳定性(Mohamed 1983)、完全非线性Euler 方程中任意大振幅的电毛细孤立波(Guan 2022)等. 在过去的几十年间, 对电流体界面波非线性约化模型的研究往往集中于二维流体, 流体力学家和应用数学家建立了大量新的多尺度非线性模型, 感兴趣的读者可参看D. T. Papageorgiou 教授于2019 年发表在《流体力学年鉴》上的综述文章(Papageorgiou 2019).

本文聚焦三维流体系统中非线性电流体界面波的多尺度建模. 研究对象限于无黏不可压缩流体, 讨论槽道内上下叠放的两种不相溶电介质流体在电场力、重力、界面张力共同作用下的界面波动问题. 为简单起见, 假设每层流体的运动都是无旋的; 在界面有形变的情况下, 水平电场通过Maxwell 应力作用于界面; 第3 节证明该自由界面问题构成一个Hamilton 系统. 第4 节引入处理位势方程的关键-Dirichlet-Neumann算子,并在此基础上重写Hamilton量中的动能与电势能. 第5 节提出一种利用Dirichlet-Neumann 算子的解析性质建立非线性多尺度模型的普适方法, 并以“上层深水、下层浅水”为例给出详细的推导过程, 建立全新的约化模型. 结论与进一步的拓展在第6 节中讨论.

2 问题的数学描述

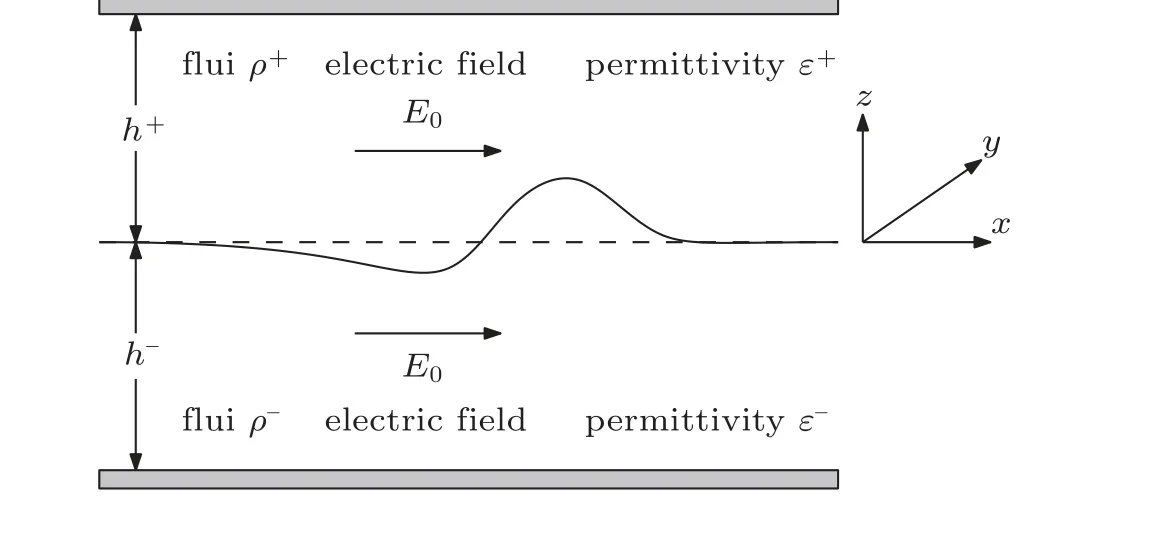
图1水平电场下两层电介质流体间界面波问题的概图.

从物理上来讲, 有关电场的无穿透边界条件用于模拟电绝缘壁(见Barannyk 2015, Guan 2022). 方程(1)(2)(4)(5)(7) ～ (11)构成水平电场下理想电介质流体界面问题的完整数学描述.

3 Hamilton 原理

这一节将证明, 在假定方程(1)(2)和(7) ～ (11)成立的前提下, 式(4)和式(5)构成一个Hamilton 系统. V. E. Zakharov 在1968 年开创性地给出了水波动力学的Hamilton 原理(这一经典工作的中译本请见(Zakharov 2021), 读者也可阅读综述(张宝善 1998)以了解更多相关内容).以Zakharov 为代表的前苏联波动力学学派应该也知道电流体界面力学的Hamilton 原理, 尽管他们并没有给出任何推导过程(如Zubarev 2013). 但事实上, 他们关于该问题在深水情形下的结论并非显而易见, 这里我们给出任意水深情形下的详细证明.

在不存在电场的情况下(等价于令E0=0 ), 式(4)和式(5)亦构成Hamilton 系统, Hamilton 量为系统的总能量H, 而两个正则变量则为界面形变η和广义冲量ξ=ρ-φ-(x,y,η,t)-ρ+φ+(x,y,η,t)(界面上下速度位势的线性组合), 即

其中动能Ek和势能Ep的具体表达式为

比较式(21)和式(9), 即完成证明.

4 Dirichlet-Neumann 算子

ξ±=φ±(x,y,η,t)W=W±(x,y,η,t)

定义 和 为未知函数在界面上的值, 根据方程(1)(2)及上下壁处的无穿透条件式(10)、式(11), 界面上未知量的法向导数可表示为

其中 Δ =∂xx+∂yy是平面上的Laplace 算子. 利用Dirichlet-Neumann 算子, 方程(8)可改写为

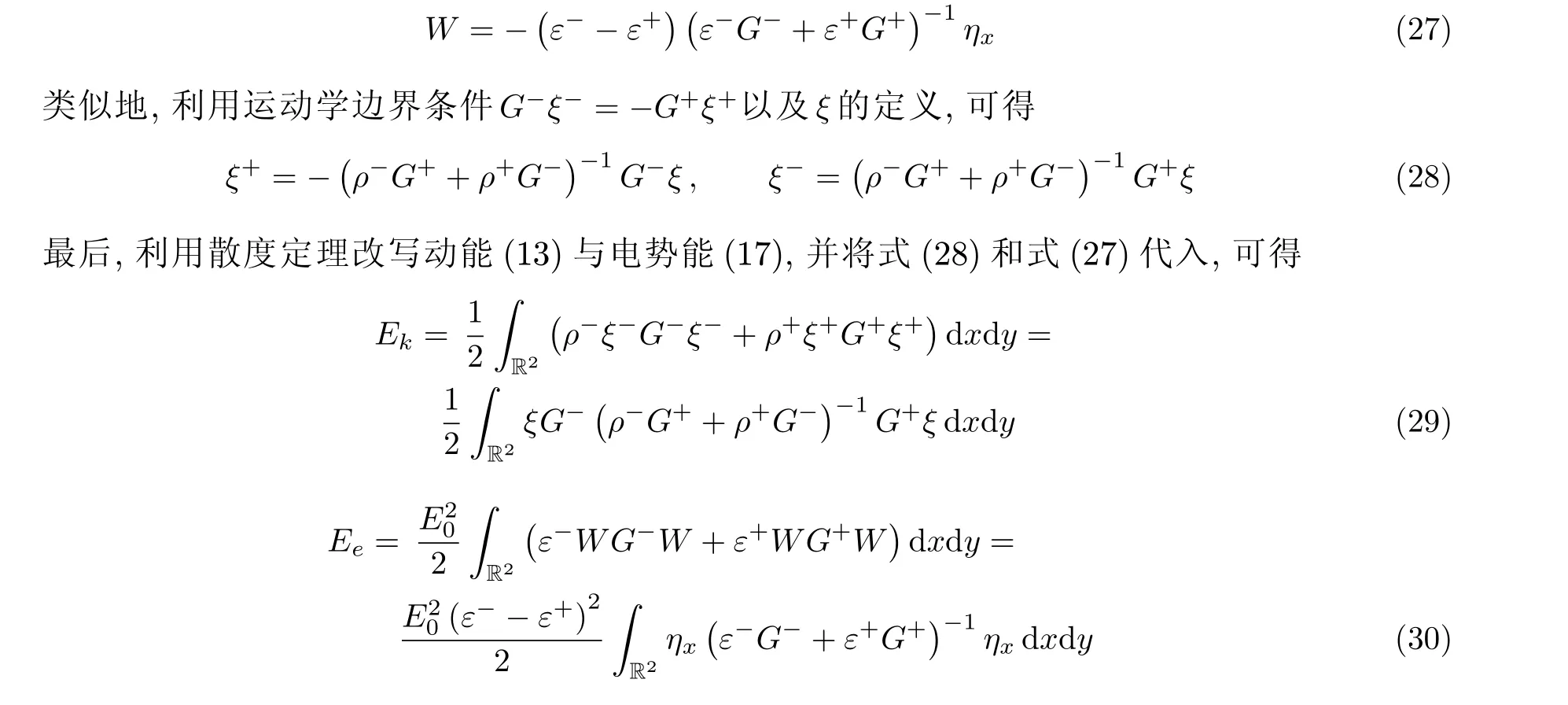
5 多尺度建模

约化模型(43)和(40)中存在“块状波”解(lump), 一种在三维空间中完全局域化的行进波(即局部波动在保持形状不变的情况下以固定速度直线传播). 这里采用修正的Petviashvili 迭代技巧计算块状波, 具体的数值格式可参看(Wang 2022), 此处只简单叙述结果. 假设块状波沿x方向以速度c进行传播, 图2 给出了c=0.5 时块状波波形, 此时其他参数为:μ=0.1 ,Bo=10 ,Be=1,R=0.99 .

水平电场下的界面波表现出有趣的动力学行为, 尤其是在抑制Rayleigh-Taylor 不稳定性、界面的触壁奇性、自相似解等方面(低维问题的相关结果可参看Barannyk 2015), 许多行为可以用目前建立的约化模型来展现; 因篇幅原因, 关于方程组(43)和(40)的行波解全局分岔机理、系统稳定性与动力学等问题的研究留待将来.

若假设界面振幅远小于h-, 方程组(43)(40)可简化为弱非线性的二维Benjamin 方程(感兴趣的读者可参看(Guan 2022), 尽管那篇文章中只给出了一维Benjamin 方程的推导过程). 从上面的例子可以看出, 在长波、短波、小振幅波、有限振幅波等不同尺度的假设之下, 利用Dirichlet-Neumann 算子的解析性质, 可合理展开Hamilton 量中的动能与电势能, 截断后取变分导数即可得到各类约化模型. 特别地, 不难得到“上层浅水、下层浅水”的弱非线性弱色散的Boussinesq 型方程组与Kadomtsev-Petviashvili 型方程, 以及“上层深水、下层深水”的全色散弱非线性的Whitham 型方程. 囿于篇幅, 这里不再一一赘述推导过程, 有兴趣的读者可自行验证.

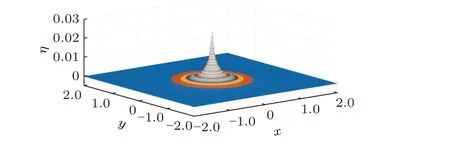
图2典型的“块状波”波形图, 波移动的速度为 c =0.5 , 其余的参数为: μ =0.1 , B o =10 , B e =1 , R =0.99 .

6 结论与讨论

本文研究两种电介质流体间的界面在水平电场作用下的波动问题. 证明了该自由边界问题具有Hamilton 结构, 其Hamilton 量为总能量, 而正则变量为界面形变η与广义冲量ρ-φ--ρ+φ+.引入位势问题中至关重要的Dirichlet-Neumann 算子可改写Hamilton 量中有关动能与电势能的部分. 在此基础上, 利用Dirichlet-Neumann 算子的解析性质, 可以将原来的三维问题简化为二维问题. 最后, 按照所研究问题的时间与空间尺度的具体情况, 对Hamilton 量进行展开与截断, 通过计算变分导数即可得到所需的约化模型. 这一套渐近方法具有一定的普适性, 可导出各类多尺度模型, 文章仅以“上层深水、下层浅水”为例进行了详细说明. 相比于作者在(Guan 2022)中提出的多尺度建模方法, 本文提出的方法由于直接截断Hamilton 量进行变分, 所得的约化模型天然具有Hamilton 结构, 是更为直截了当的方法.

在无黏不可压缩的假设之下, 因水平电场为电介质流体系统提供了更多的色散效应, 故起到了稳定系统之作用. 但是水平电场的存在也破坏了系统的对称性, 这一点非常明显地展示在色散关系式(41)和式(44)中, 也就是说从线性理论层面来看, 水平电场的稳定作用对那些垂直于电场方向传播的波而言是无效的. 最后需要指出, 使用Hamilton 正则变量来构造模型并不一定是最优的, 某些时候直接使用非正则变量所得到模型形式上更为简洁(见(Guan 2022)中的讨论).

致 谢 感谢中国科学院力学研究所的许葛幸在此领域与作者的有益讨论. 本项目受中国科学院B 类战略先导(XDB22040203)与中国科学院青年交叉团队项目的资助.