微积分中一元函数求导方法探讨

张芬,吴红星,石黄萍,周富磊

(1.上饶师范学院 数学与计算机科学学院,江西 上饶 334001;2.上饶中学,江西 上饶 334001)

微积分的主要研究对象是初等函数,初等函数是由常数和基本初等函数经过有限次四则运算复合而成的[1－2]。近年来,许多学者对函数的求导方法进行了研究[3－10]。文献[3－4]讨论了复合函数的求导法则;文献[5]给出了隐函数的几类求导方法;文献[6－7]研究了幂指函数的求导方法;文献[8]研究了利用辅助函数来求解幂指函数的导数,求导的过程相对简便和易于理解;文献[9]讨论了如何求解由参数方程所组成函数的导数;文献[10]阐述了如何高效地求解高阶导。本文拟对微积分中函数求导的若干方法进行研究,分析相关函数求导时的易错点,为教师在函数求导方面的教学提供便利,为大学生学习函数求导提供帮助。

1 导数的四则运算法

引理1[1]如果函数u(x)和v(x)在点x处具有导数,则他们的和、差、积及商(除分母为零的点外)都在x点处有导数,并且:

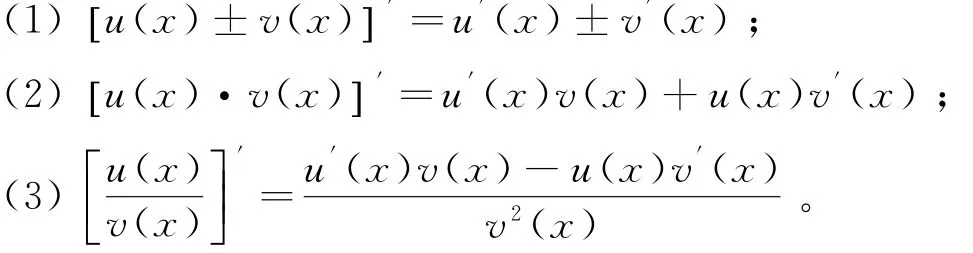
引理1中的法则(1)和(2)适用于有限个可导函数的情形。

例1 已知y＝sinx·cosx－ex＋arctanx－ln2,求y′。

解:由求导的四则运算公式可得:

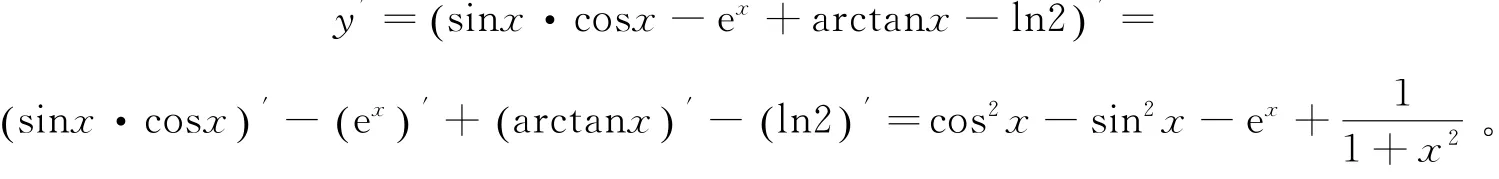
说明:常数的导数恒为零,例如:C(任意常数)、e2及lna(其中a为任意常数)等等各种形式的常数表达式,对其求导所得的导函数均为零。学生在求导的过程中往往会被e2和lna的常数形式所误导,对其求导的时候用指数函数和对数函数的公式去运算,那将导致所求结果错误,所以在求导的过程中一定要牢记无论何种形式的常数对其求导都等于零。

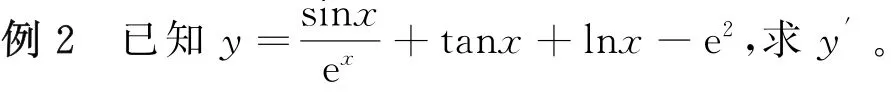
解:由求导的四则运算公式可得:

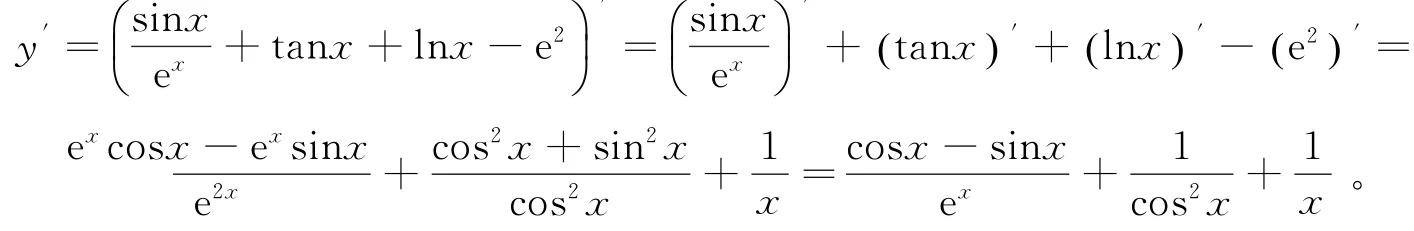
2 复合函数的求导法

设u＝u(x)在点x处可导,函数y＝f(u)在点u＝u(x)处可导,则可得复合函数y＝f(u)在点x处可导,且其求导公式可以推广到多个中间变量的复合函数求导上。

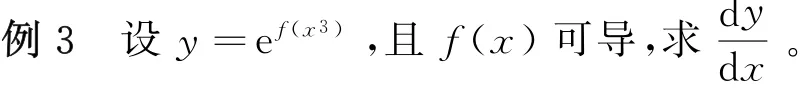
解:由题意可得,本题是复合函数,故由复合函数的求导法可求出其导数,现分别给出错误解法和正确解法,如下:

错误解法:函数y＝ef(x3)可看成由y＝eu,u＝f(x3)复合而成,故:

正确解法:函数y＝ef(x3)可看成由y＝eu,u＝f(x3),v＝x3复合而成,故:

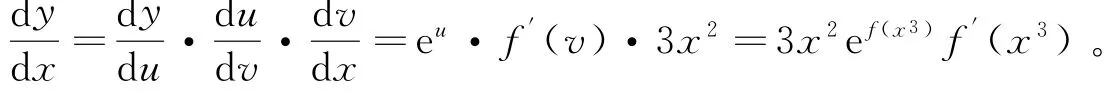
说明:求导时我们应采取“剥洋葱”的方式,一层层往里“剥”。例3求导时学生往往只记得对f关于x求导得f′,而忽略了内部x3关于x求导,最终导致结果错误。

3 隐函数的求导法

首先,设为F(x,y)＝0隐函数;其次,对F(x,y)＝0两边同时关于x求导,求导的过程中把y看成y(x),再利用复合函数的求导法;最后,通过整理可得到隐函数的导数。

例4 设y4－sinxy－ex＋ln2＝0,求y′。

解:由题意可得,所给的函数是隐函数,故求导的时候用隐函数的求导法,现分别给出错误解法和正确解法,并给出解决此类题目时的注意事项,如下:

错误解法:

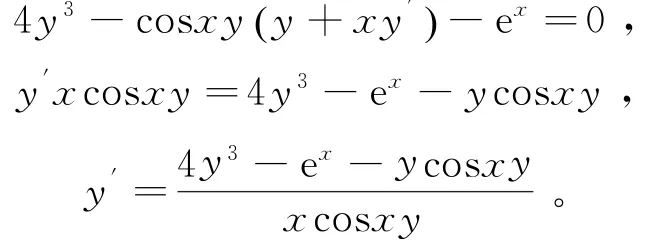
正确解法:

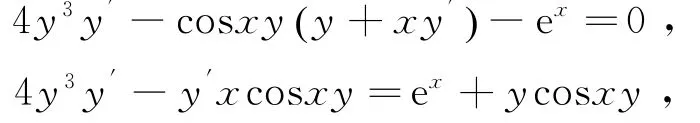
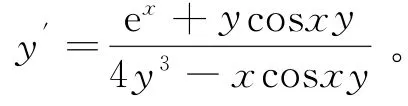
说明:其中y4关于x求导时,应将y看成y(x),即y4＝y4(x),故令u＝y(x),可得y4(x)＝u4,所以求导的时候利用复合函数的求导法可得:

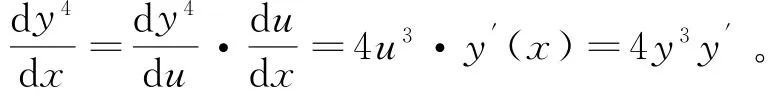
在求解此类隐函数的导函数时,学生容易错误地认为y4关于x求导等于4y3,忽略了y是关于x的函数,即y＝y(x),从而忘记对y(x)关于x求导。

4 幂指函数的求导法

从幂指函数y＝u(x)v(x)的形式上看,我们无法直接将其归纳为幂函数或者指数函数,因为它既有幂函数的性质也有指数函数的性质,所以在求导的过程中我们不能直接用幂函数的求导法则或者指数函数的求导法则。幂指函数的求导公式在微积分课本中没有直接给出,在此我们将通过一个例题引入相关的求导法则。

例5 设y＝xcosx,求y′。

解:本例题无法直接通过求导公式求导,所以在此得通过构造函数,然后再对其求导,现给出两种解法:

解法1:关于y＝xcosx两边同时取对数,可得lny＝lnxcosx＝cosxlnx,然后根据隐函数的求导法,分别对lny＝cosxlnx的两边关于x求导,可得:

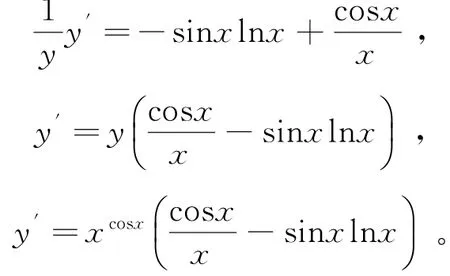
解法2:对于幂指函数y＝xcosx,可通过指数对数恒等变形,可得y＝elnxcosx＝ecosxlnx,则:

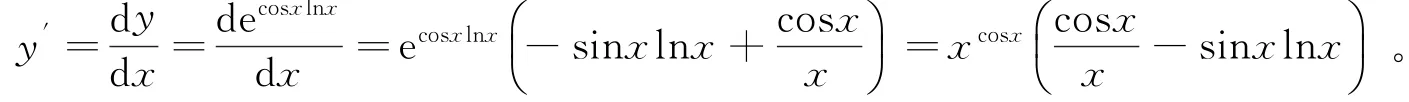
由以上两种方法,我们可以归纳出幂指函数y＝u(x)v(x)的求导公式如下:

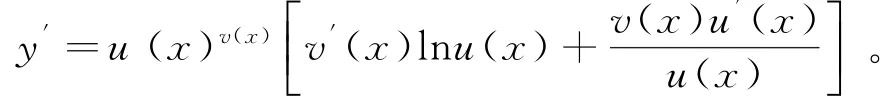
现给出幂指函数的求导公式证明如下:

证明:因为y＝u(x)v(x)关于x可导,所以,u(x),v(x)在定义域内连续和可导,故由导数的定义可知:

所以:

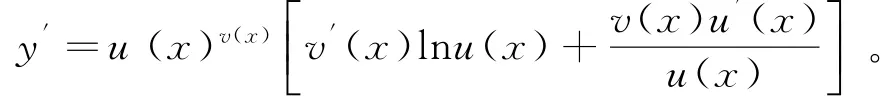
证毕。

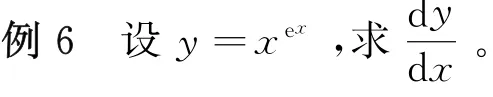
解:幂指函数y＝xex可看成由u(x)＝x,v(x)＝ex复合而成,则运用幂指函数的求导公式可得:

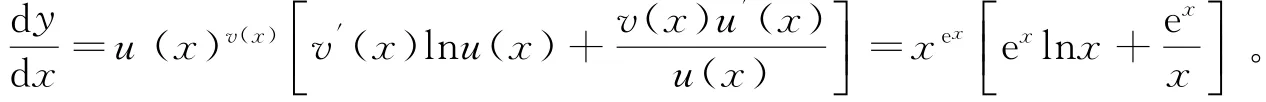
由本题可知,若记住了幂指函数的求导公式,则在解决幂指函数的求导问题时可以事半功倍。

5 参数函数的求导法

除了上述几种类型的求导法外,还有参数函数的求导法,也即y＝y(t),x＝x(t),此时让我们求从所给的式子中,不难发现,x和y之间没有直接关系,而是通过一个中间变量t联系在一起,由此可得:

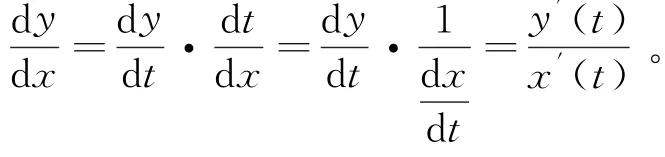
相应可得y关于x的二阶导,即:

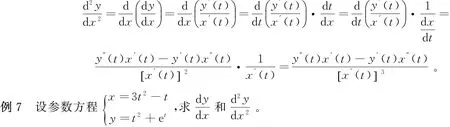
解:由参数方程的求导法则可得:

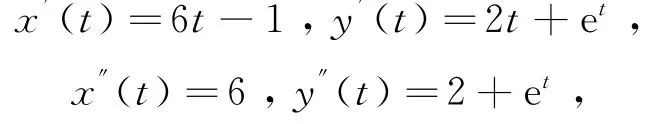
所以:

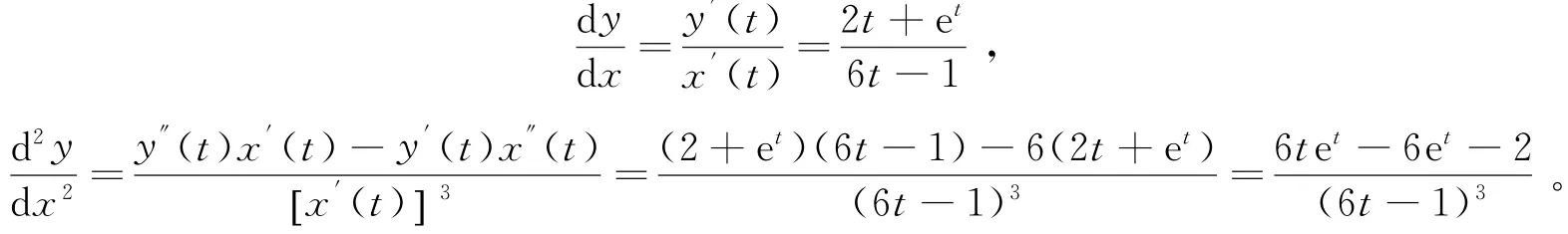
说明:学生关于参数函数求一阶导时,几乎不会碰到易错点,但对于求参数函数的二阶导时,往往会犯相同的错误,即:只记得在参数函数一阶导的基础上对变量t求导,而忽略了分母的x也需对t求导,最后导致结果出错,所以在求参数函数的二阶导时,要牢记分子、分母需同时对t求导。