指数函数的fpga实现及算法优化
刘 恒,钟 俊,刘 辉
(安徽职业技术学院,安徽 合肥 230011)
0 引言
在超越函数中,指数函数的应用十分广泛。实现指数函数的方法有很多,包括查表法、旋转迭代、泰勒展开等[1]。查表法需要较大存储空间,特别是高精度情况下,资源耗费比较明显。旋转迭代依赖于流水线技术,精度要求较高时,需要较多的时钟周期完成一次求解。泰勒展开涉及到大量的乘、除法器,运算速度不高。本文在切比雪夫多项式函数逼近的基础上进行优化设计,进一步减少fpga资源消耗,提高运算速度。
1 切比雪夫多项式和函数逼近
1.1 切比雪夫多项式
切比雪夫逼近以切比雪夫多项式为基础,切比雪夫多项式可以写成如下形式[2]:

虽然Q k(x)是类三角函数形式,但经过变形之后,可以将式(1)变为多项式的标准形式,部分多项式可以写成如下形式:
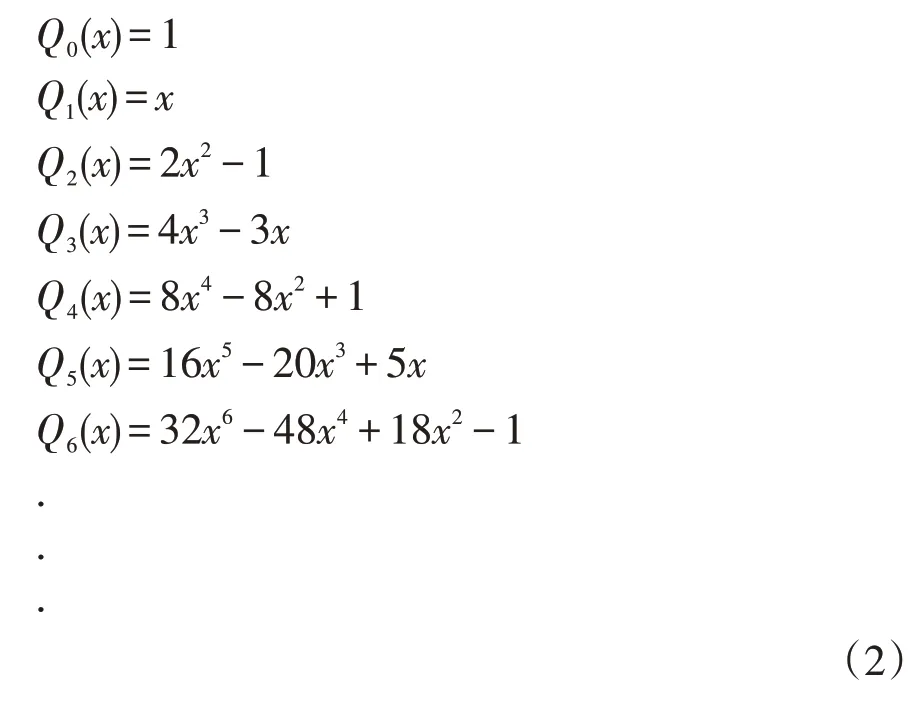
切比雪夫多项式符合如下迭代规则:

1.2 函数逼近
切比雪夫函数逼近可以写成:

所有切比雪夫多项式具有相互正交的特点,因此得到的双向变换都是独一无二的。使用式(4)切比雪夫函数逼近要明显优于使用泰勒函数逼近(式(5))。
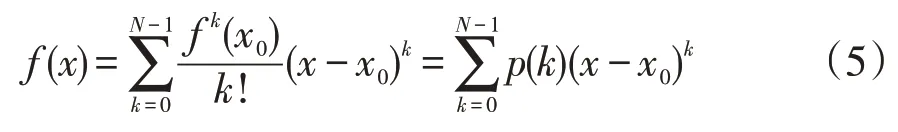
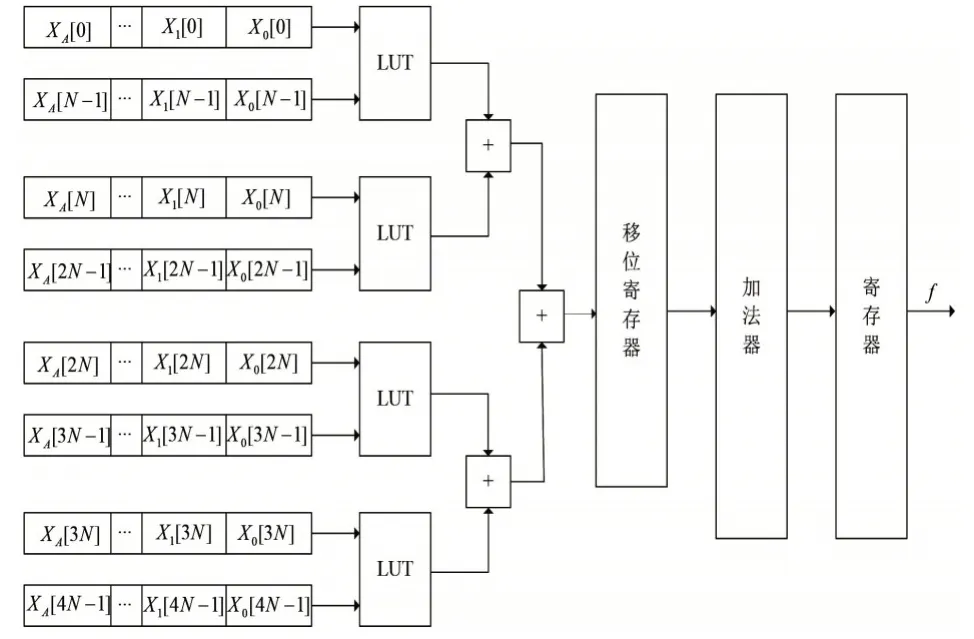
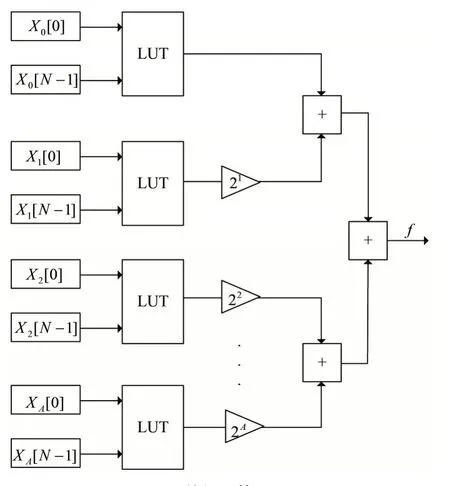
原因如下:首先,式(4)是非常接近于(但不严格等于)函数逼近这一非常复杂问题的最优解,而且能够保证最大误差最小,也就是l∞范数的最大值max(f(x)-f(x))→min;其 次,式(4)的 剩 余 项M< 用切比雪夫系数计算的16位多项式量化应采用如下的公式: 需要保证0≤x≤1,如果输入不在这一范围之内,就需要用恒等式esx=(ex)s进行缩放。 其中s=2k是2的幂,在完成指数计算后还要继续进行k次平方运算。 在具体的硬件设计过程中,积之和可以采用分布式算法来实现[3]。根据函数表达式,计算一个函数值需要N个mac(乘累加)。采用流水线技术能够加快运算速度,但是也十分有限。如果速度优先,可以采用并行乘法器,其代价是占用大量的乘法单元,造成资源浪费。如果已知每一项的系数,乘积项就可以写成常数乘法的形式。这是分布式算法的实现基础。分布式算法实质上是用查找表取代乘法器。在速度与资源占用上,相比传统的乘法器实现方式,分布式算法更胜一筹[4]。 分布式算法原理: 假设h(n)已知,x[n]未知。无符号分布式算法假设x[n]可以写成下列表达式x a[n]∈[0,1],其中x a[n]是x[n]的第a位。 内积f可以表示为: 可以用一个LUT来实现f(h(n),x a(n))的相关运算。首先计算得到一个LUT,LUT由2N个元素构成。当输入为一个N位的输入向量x a=[xa[0],x a[1],...,x a[N-1]]时,可以用LUT查找到相应的输出,输出为f(h(n),x a(n))。每次查找的结果乘相应的权值并累加。在N次查询结束之后,得到函数值f,如图1所示。 图1 无符号da原理图 (1)LUT简化设计 LUT的规模与输入系数N成指数关系[5]。如果N过大,可以将单个N输入的LUT拆分成多个规模较小的查找表相加。这一改进可以极大地降低资源消耗,并且几乎没有影响运算速度。假定内积的长度为LN,可以表示为: 拆分LN项的和,变为L个独立并行的N阶DA的LUT,结果如下: 如图2所示,实现1个4N的DA设计,还需要3个加法器。表的规模从1个24N×A的LUT缩小为4个2N×A的表。考虑到fpga硬件资源,取L=2,N=3,或L=1,N=6。 图2 简化LUT原理图 (2)并行运算 采用并行计算可以加快DA体系结构的运算速度,这一改进必然会占用更多的资源[6]。DA体系结构如果按照串行方式进行运算,在每个时钟周期只能完成1bit数据的接收处理。采用并行计算可以同时接收处理Mbit数据,运算速度能够加快M倍。图3为实现最大速度所需的字并行体系结构。最大速度要求为每个位向量x a[n]准备一个单独的LUT(各个LUT完全一样)。速度提升M倍的代价是资源同等程度翻倍。在fpga硬件实现过程中,如果N为4个或8个,这一改进就极具意义。 图3 并行运算原理图 在本实验中,采用quartus12.0进行综合验证,芯片为altera公司的CYCLONE系列。利用Modelsim 6.5软件进行Verilog仿真。优化结果如表1所示。Modelsim仿真如图4所示。 表1 优化前后性能比较(量化位数16bit) 图4 Modelsim仿真结果 本文用切比雪夫多项式对指数函数进行了函数逼近,并用Modelsim对结果进行了仿真验证。在函数的实现过程中,采用分布式算法进行优化。在优化过程中,通过采用多个低维度查找表和并行运算,达到减少芯片面积和提高运算速度的效果。这一方法同样适用于其他超越函数的实现过程,具有普遍意义。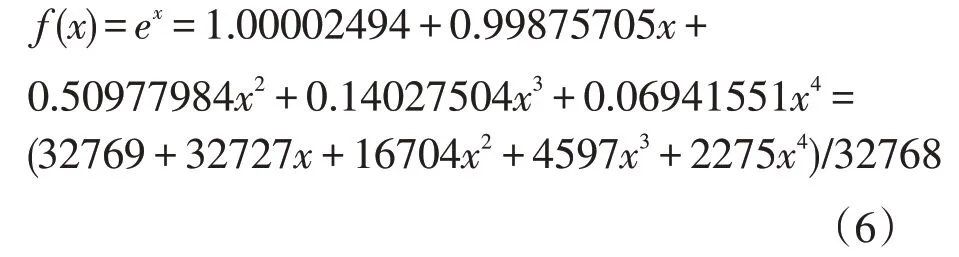
2 分布式算法及优化
2.1 分布式算法基础


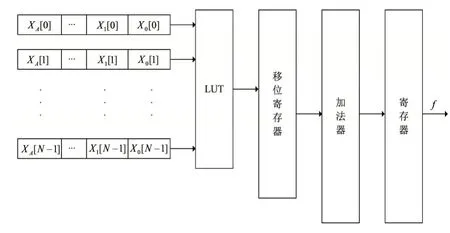
2.2 分布式算法优化
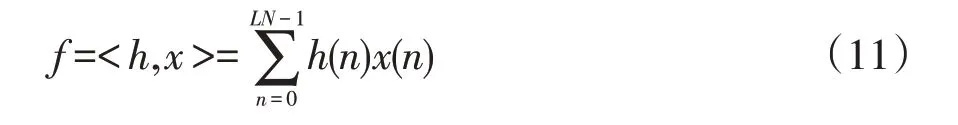
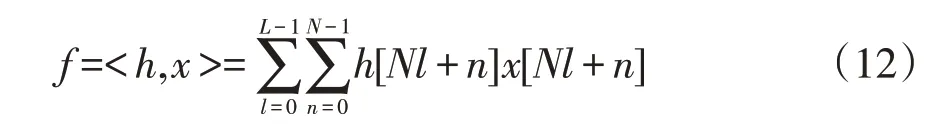
3 优化仿真结果
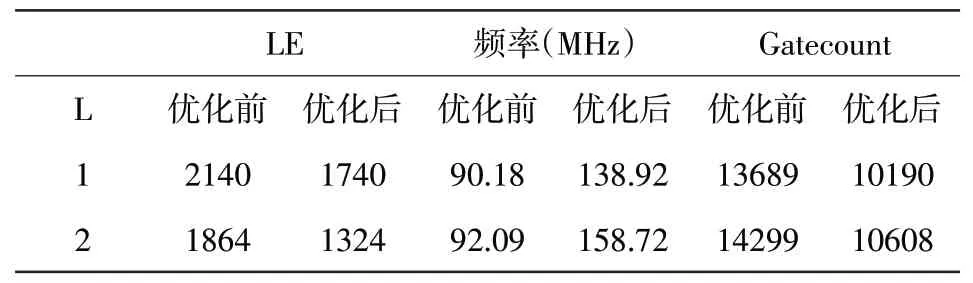
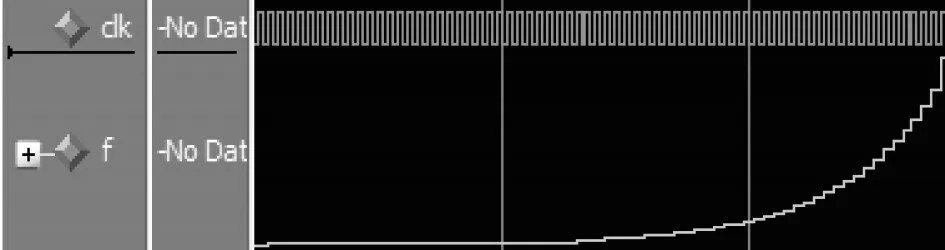
4 结语

