仿特斯拉阀结构新型槽端面干气密封的数值研究

王 衍, 徐 慧, 谢雪非, 孔康杰, 胡 琼, 谢晨卓, 蔡张伟

(1. 江苏海洋大学 机械工程学院, 江苏 连云港 222005;2. 江苏省海洋资源开发研究院, 江苏 连云港 222005;3. 江苏海洋大学 海洋工程学院, 江苏 连云港 222005)

干气密封(Dry gas seal, DGS)作为动压型机械密封的典型代表，已广泛用于各种高端流体机械装置中[1-2]，动压型机械密封的特殊之处及核心技术在于端面结构的与众不同，正是由于这一特点，表面槽型的千变万化已成为动压密封领域研究最活跃的部分. 不同类型槽型的密封性能和使用工况千差万别，目前典型的密封端面结构以多孔端面(Micro-pores)、对数螺旋槽(Logarithmic spiral groove)及其他变异槽型为主要代表. Etsion等[3]最早于1996年提出了多孔端面动压机械密封的研究原型，通过在动环或静环端面开设各类孔径、孔深和不同分布的微孔，密封环旋转时每个微孔都类似于1个微型动压轴承，产生的流体动压效应使端面分离形成非接触. 1999年，Lai等[4]对各类不同槽深的动压槽型进行系统研究，毫米级深槽包括半圆形、矩形、月牙形、三角形以及各种复合槽型，微米级浅槽包括对数螺旋槽、径向直线槽、斜直线线槽和圆弧槽等.

对数螺旋槽干气密封凭借优异的动压效应和高气膜稳定性，是目前研究和应用最广泛的槽型，也是动压密封和动压轴承中的首选槽型结构[5-6]. 近几十年来，国内外学者一直在探索比对数螺旋槽综合性能更好的槽型. Salant等[7]和Chen等[8]研究对比了斜直线槽和超椭圆曲线槽与对数螺旋槽的开启性能及泄漏特性，吴宗祥等[9]和胡丹梅等[10]计算分析了直线槽、圆弧槽及对数螺旋槽的稳态特性，结果都表明对数螺旋槽密封在高工况下的动压特性独具优势. 许多学者还围绕螺旋槽进行了诸多有意义的改良优化，1999年，宋鹏云等[11]提出了一种由内外同向螺旋槽和密封坝组成的内外螺旋槽密封，可用作内装内流或外装外流机械密封. 2000年，Zheng等[12]开发了一种新型双列螺旋槽端面密封，适用于航空发动机中的大直径和高转速工况. 为了实现双向旋转，2001年，天津鼎铭密封公司通过将螺旋槽对称布置，发明了一种可双向旋转的螺旋槽密封结构[13]. 2004~2009年，清华大学王玉明等[14-16]对螺旋槽密封开展一系列深入研究，先后提出了油膜双螺旋槽端面密封和双列单向人字形干气密封等槽型结构，并进行了试验验证和工程试用，最终成功应用于石油石化行业压缩机中. 2013年，丁雪兴等[17]以螺旋槽的流场流线为模型提出了一种拟合曲型槽型，一定工况下的动压效果比螺旋槽略有提高. 2015年，江锦波等[18]提出一种仿鸟翼微列螺旋槽端面干气密封结构，一定工况下，该槽型的密封性和稳定性较对数螺旋槽都有显著提升(轴向气膜刚度增幅达到30%，泄漏率降幅达到10%)，并于2019年提出一种几何表征能力更强的广义对数螺旋槽[19]，相较于传统对数螺旋槽，在气膜刚度上有一定提升，近期基于微段组合提出的广义对数螺旋槽结构模型，进一步建立了广义对数螺旋槽结构参数定义体系[20]. 可见，围绕各类槽型的设计、研究和改进，国内外学者已进行了诸多有益探索，均为获得更好动压效应和更大刚度的槽型结构.目前而言，对数螺旋槽的研究和应用已日臻完美，凭借普通线性槽的设计和改良很难获得比对数螺旋槽性能更全面的槽型，且气膜刚度直接影响槽型的运行稳定性，进一步提升的难度比较大. 基于此，本文中突破传统线性槽设计的束缚，借鉴特斯拉阀结构的单向导通特性，提出了一种区别于传统对数螺旋槽动压集聚特点的新型动压槽型-特斯拉阀型. 并以特斯拉阀型干气密封为研究目标，系统研究此类新式槽型的多工况密封特性，对比分析对数螺旋槽和特斯拉阀型在不同工况和几何参数下的开启性、密封性和稳定性，以期为此类新型槽型的实际工业应用提供理论指导.

1 计算模型

1.1 对数螺旋槽干气密封

图1所示为经典对数螺旋槽干气密封(Spiral groove dry gas seal, S-DGS)端面槽型结构，两条对数螺旋线和圆弧线共同组成了1个完整的螺旋槽型. 对数螺旋槽控制方程如式(1).

式中：r为极径，rg为起始极径，这里为干气密封根径，α为螺旋角，θ为极径r处的对数螺旋线与起始点间的周向夹角，对数螺旋槽干气密封的基本几何参数列于表1中.

表1 螺旋槽干气密封几何参数Table 1 Geometric parameters of S-DGS

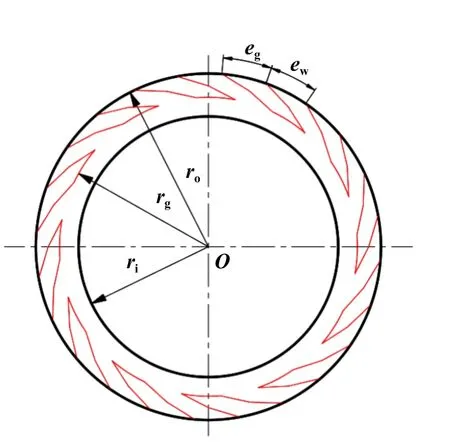
Fig. 1 Schematic diagram of logarithmic spiral groove图1 对数螺旋槽示意图

1.2 特斯拉阀结构及工作原理

特斯拉阀是由塞尔维亚裔美籍科学家尼古拉·特斯拉提出且以自己名字命名的一种单向导通气流阀，并于1920年申请了发明专利. 特斯拉阀的主要特点在于其整体无任何活动部件，仅利用空间结构推动气体流动，无需输入能量即可实现流体的单向导通特性[21].

如图2所示，流体正向流动(从右至左)与反向流动(从左至右)差别巨大，正向流动时，流体能够绕过所有的翼状障碍进而畅通无阻地从右边流至左边，并且因流动压力而获得加速效果；但流体反向流动时，流体每经过1个通道，就向上/下进入1个翼状障碍，回流会使流动发生阻塞效应且增大压头，阻碍流体整体向前流动. 且翼状障碍越多，流体向前推进的阻力就越大，导致特斯拉阀独特的单向导通效果. 研究表明[22-23]，对于两个通道的特斯拉阀，正向和反向流动的阻力差距可达200倍. 理论上，如果翼状通道足够多，特斯拉阀结构可将流体加速至超音速，而相反方向的流动会使翼状障碍区域压头增大，并逐级建立起多组回流压力区域，形成流体动压效应.

Fig. 2 Schematic diagram of the Tesla valve图2 特斯拉阀原理图

1.3 特斯拉阀型干气密封

基于特斯拉阀结构的回流阻塞效应，认为利用这一特性应有利于进一步提升微尺度流场间的流体集聚效应. 同时参考特斯拉阀结构的翼状障碍几何特征，建立如图3(a)所示的端面槽型结构，该槽型由主阀道、支阀道及一定阀道半径形成的多个翼状障碍组成. 基于流体动压密封基本原理，特斯拉阀结构采用单侧贯穿形式，有利于更好地形成集聚效果；考虑旋转流场中流体的流线特点[17]，主阀道翼状通道宽于支阀道，同时整个阀型采用曲线造型. 由图3可知，由于密封端面宽度的限制，翼状通道数量不能太多，图中所示结构具有4个翼状结构.

类似于螺旋槽干气密封，特斯拉阀型干气密封(Tesla valve-type dry gas seal, TV-DGS)也呈周期性分布，为提高计算效率及网格划分质量，取1个周期内的特斯拉槽进行分析计算，计算区域如图3(b)所示. 由与内外环同心的圆心O及相应阀槽半径Rv可确定特斯拉阀槽型主阀道位置，m为主阀道宽度，t为支阀道宽度，re为翼状结构半径. 翼状结构由直线和圆弧线(边侧弧线半径rs、槽底弧线半径rm)组成，翼状结构圆心位置及线段起始点由图示的夹角α、支阀道内外径(re1、re2)及各交点确定，左侧第一个翼状通道角度由β设定，如图3(b)所示，具体数值列于表2中.

Fig. 3 Geometric model of TV-DGS图3 特斯拉阀型干气密封几何模型

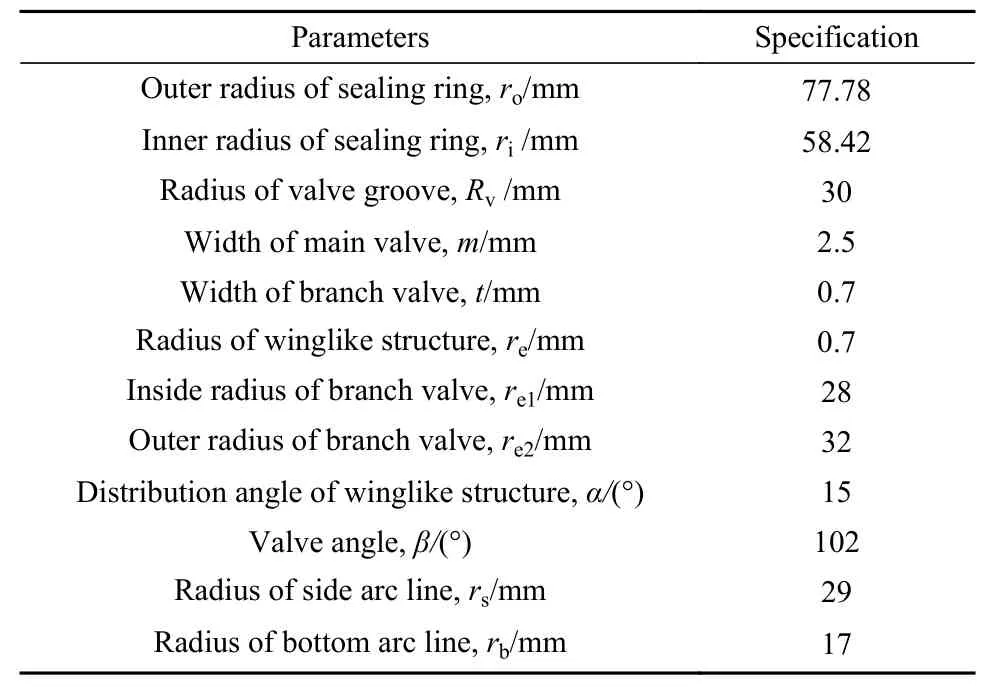
表2 特斯拉阀型干气密封几何参数Table 2 Geometric parameters of TV-DGS

2 分析模型

2.1 基本假设

基于近年来特斯拉阀的相关研究[24-25]及动压机械密封端面流体介质属性特点[26-27]，作如下假设：

(1) 端面流场中的气体为连续介质流动；

(2) 流场中气膜的温度和黏度相等；

(3) 气体分子与密封表面牢固吸附，无相对滑移；

(4) 忽略密封副变形对介质流动的影响；

(5) 忽略气体重力的影响；

(6)密封副在运行过程中始终保持平行，不考虑表面粗糙度的影响.

为进一步探究新式槽型在高速下的性能表现，最高计算转速设为100 000 r/min，此时需要对是否考虑惯性力和离心力进行讨论(鉴于研究对象为稳态流动，这里不考虑流体流沿沟槽的局部惯性力影响). 依据文献[28]的结果，是否考虑惯性力和离心力的影响可依据式(2)进行判断.

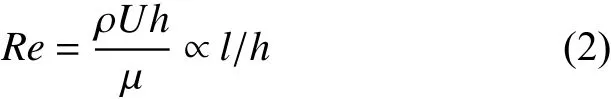
其中：Re为雷诺数，ρ和μ分别为流体的密度和黏性系数，U为密封环平均旋转线速度，l为特征长度，h为密封副间膜厚[29]. 当Re与l/h可比拟或同一数量级时，必须考虑惯性力和离心力的影响，如果差距较大时，即可忽略惯性力的影响.

由表1中密封模型几何参数，取研究工况上限值(h=1 μm，N=100 000 r/min)，带入相应数值后可得上式分别为Re=49.43＜＜l/h=77 780，两者差距较大，即忽略气体惯性力和离心力的影响.

2.2 控制方程

依据基本假设，选用Fluent流体计算软件对特斯拉阀槽型内的流体流动进行稳态数值模拟，气膜压力控制方程如下：

其中：气膜厚度分别为(1)槽区：h(r,θ) =ho+hg；(2)非槽区：h(r,θ) =ho.ho为非槽区气膜厚度，hg为槽深，θ为单位角速度所转过角度，ω为角速度，p为气膜压力.

边界条件有两类：

a. 强制性边界条件：外径处，有P=Pin(外压)；内径处，有P=Pout(大气压).

计算前，还需要对流体流态进行判定，流体动压密封流场情况复杂，存在管流、缝隙流及旋转绕流，不能单纯依靠经典雷诺数模型进行流态判断[30-31]，对此类流场的流态选择问题存在较大争论[32-34]，计算时选择层流还是湍流模型学术界尚未有统一定论[35-36]. 近期研究表明[37]，层流和湍流对密封性能参数的影响规律整体基本一致，主要表现为具体数值的差别，鉴于此，在满足连续介质假设时，可以通过直接求解(DNS,direct numerical simulation)实现对流场的分析计算.Fluent求解器中的Laminar模型实际为基于连续假设条件的一定网格和步长要求下对方程的直接求解，对计算机的性能有一定要求，鉴于此，本文中计算采用Laminar模型及SIMPLEC算法进行亚松弛迭代计算[38].采用中心差分进行扩散项离散，对流项计算采用二阶迎风格式，连续方程和动量方程的压力值迭代精度相对值设为10-5，能量方程设为10-6.

瞬态计算基于大涡模拟(LES)[39]将瞬时脉动分解为大尺度脉动和小尺度脉动，利用可解尺度的N-S方程直接求出大尺度脉动，小尺度脉动需通过亚格子应力模型(Sub-grid scale model)进行模拟求解. 采用密度加权(Favre)法对传统大涡模型进行过滤，可得可压缩大涡模拟控制方程：

其中：xi和xj(i, j=1, 2, 3)为笛卡尔坐标，i和j分别为不同方向上的单位矢量为平均密度，ui和uj为速度分量，为热传导项为总能为压强，βij为热膨胀系数，为应力张量，sij为变形张量，τij为亚格子应力(SGS)，Cp为流体的比热容，Qi为亚格子热传导，Di为亚格子黏性扩散项，Ji为亚格子湍流扩散项，αi为吸收系数.

2.3 建模及网格划分

流体动压密封微尺度流场的径向(y向)与厚度方向(z向)尺寸差别达4个数量级以上，是网格划分的难点，如处理不当会严重影响网格划分的质量，对仿真结果精度造成影响. 而特斯拉阀槽型含有多个翼状通道，进一步增大了网格划分的复杂性. 本文中采用UG软件对特斯拉阀槽型结构进行三维建模，然后导入Gambit中进行网格划分，首先将模型在z向放大1 000倍，网格划分结束后再逐次将面网格拉伸为体网格，如图4(a)所示. 这种网格划分法可较好地保证不同方向上的网格质量差别不显著，也可避免连接面上的Interface设置. 最后，导入Fluent进行仿真计算，并通过Scale设置将模型的实际尺寸进行还原.

Fig. 4 Mesh generation and independent analysis图4 网格划分及无关性分析

在系统计算前进一步开展网格无关性分析，图4(b)所示为开启力随网格数量的变化曲线. 从图中可以看出，随着网格数的增大，开启力缓慢增大且渐趋稳定，在网格数达到80万后趋于稳定. 因此，后续计算中，兼顾计算精度和效率的要求，文中选取网格数量均在100万左右.

3 计算结果与分析

3.1 压力和速度流场分布

图5所示为两种槽型在同一工况下的压力场和速度场分布，由图5(a)可以看出，TV-DGS的最大开启力(3.41 MPa)略小于S-DGS (3.97 MPa)，这主要是由于S-DGS在槽根附近具有更大面积的阻流区，所形成的高压区面积更大[40-41]，而TV-DGS的高压区域点不止1个，且1个周期内TV-DGS的高压区域面积明显大于S-DGS，这也是下文中TV-DGS开启性能提升的内在因素. 图5(b)所示为同一工况下两种槽型的速度场分布，可以看出，S-DGS的速度场为单一流线分布，槽区流向一致(流向槽底)；而右侧TV-DGS的速度场内比较复杂，在每个翼状通道与主阀道交界处，流线流向不同，出现了流体局部集聚效应，这也是图5(a)中出现多处局部高压区的内在因素.

Fig. 5 Pressure and velocity fields distribution of TV-DGS and S-DGS (h=3 μm, hg=4 μm, P=2 MPa, N=40000 r/min)图5 TV-DGS与S-DGS压力和速度场分布

3.2 TV-DGS与S-DGS性能对比分析

3.2.1 不同膜厚下的性能对比

图6所示为TV-DGS与S-DGS两种槽型的开启力和泄漏量随膜厚的变化趋势，可以看出，两种槽型的开启力均随膜厚的增大而降低，泄漏量均随膜厚的增大而增大. 不同膜厚下TV-DGS的开启力较S-DGS均有一定提高，膜厚越小提升量越显著；不同膜厚下TVDGS的泄漏量也较S-DGS略有增大，在膜厚h=3~8 μm区间内增加幅度略大. 可见，维持一定泄漏量的前提下，不同膜厚下TV-DGS具有更好的开启性能.

Fig. 6 Comparison of opening force and leakage rate between TV-DGS and S-DGS with different film thickness图6 不同膜厚下TV-DGS和S-DGS的开启力和泄漏量对比(hg=4 μm, P=2 MPa, N=30000 r/min)

3.2.2 不同槽深下的性能对比

图7所示为TV-DGS与S-DGS的开启力和泄漏量随槽深的变化趋势，可以看出，在图示槽深范围内，TV-DGS的开启力和泄漏量均大于S-DGS，且随槽深的增大，开启力和泄漏量的增加幅度越来越大，且两种槽型的开启力和泄漏量的变化趋势也基本一致，均随槽深的增大，呈现先增大后减小的趋势. 依据具体数值，当槽深hg=9 μm时，S-DGS的开启力和泄漏量最大，当槽深hg=11 μm时，TV-DGS的开启力和泄漏量最大，由图7可知，对于开启力，TV-DGS的最优槽深值大于S-DGS.

3.2.3 不同压力下的性能对比

进一步开展了不同压力下TV-DGS与S-DGS的开启力和泄漏量对比分析，如图8所示，两种槽型的开启力和泄漏量均随压力的升高而增大. 不同压力下，TVDGS较S-DGS的开启力略有增大，可见介质压力对提升TV-DGS开启力作用不显著；而不同压力下TV-DGS较S-DGS的泄漏量有一定增大，且随压力的增大，泄漏量增大幅值也略有提高.

Fig. 7 Comparison of opening force and leakage rate between TV-DGS and S-DGS with different groove depths图7 不同槽深下TV-DGS与S-DGS开启力和泄漏量对比(h=3 μm, P=2 MPa, N=10000 r/min)

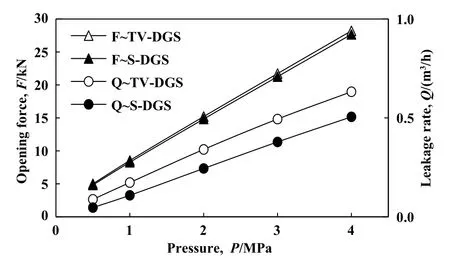
Fig. 8 Comparison of opening force and leakage rate between TV-DGS and S-DGS with different pressures图8 不同压力下TV-DGS与S-DGS开启力和泄漏量对比(h=3 μm, hg=5 μm, N=10000 r/min)

3.2.4 不同转速下的性能对比

为检验TV-DGS在不同转速下的性能表现，对两种槽型进行变转速工况研究. 由图9可知，与传统槽型类似，两种槽型的开启力和泄漏量均随转速的增大而增大，在高速工况下TV-DGS较S-DGS具有更高的开启性能. 经数据分析，当转速超过20 000 r/min后，TVDGS的开启力提升率均在10%以上，且随转速的升高，提升率呈线性增加.

3.3 几何结构参数的影响分析

由前文中可知，TV-DGS主要由主阀道和支阀道在一定曲率和宽度下构成，其中支阀道的互联又进一步构成了各种翼状结构. 为系统研究TV-DGS的工作机制，有必要深入探讨各部分几何参数对密封性能的影响规律及趋势.

(1)主阀道宽度Bm

Fig. 9 Comparison of opening force and leakage rate between TV-DGS and S-DGS with different speeds图9 不同转速下TV-DGS与S-DGS开启力和泄漏量对比(h=3 μm, hg=5 μm, P=2 MPa)

主阀道是TV-DGS中泵入流体的主要流动通道，其宽度的变化对密封性能有较大影响. 由图10可知，随着主阀道宽度Bm的增大，开启力和泄漏量均有较大变化，呈现先增大后减小的变化趋势. 最大开启力出现在Bm=5 mm左右处，最大泄漏量对应的Bm约为4.5 mm，随着主阀道宽度的增大，泄漏量的降低趋势快于开启力. 因此，为合理控制泄漏且谋求较大开启力，主阀道建议取值区间为Bm=4~6 mm.

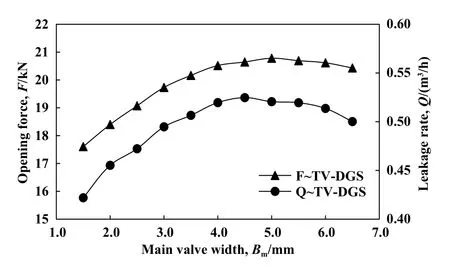
Fig. 10 Influence of main valve width on opening force and leakage rate (h=3 μm, hg=4 μm, P=2 MPa, N=40000 r/min)图10 主阀道宽度对开启力和泄漏量的影响

(2)支阀道宽度Bt

如图11所示，支阀道宽度Bt对密封性能的影响也较大，随着支阀道宽度的增大，泄漏量呈线性持续增大趋势；而开启力随支阀道宽度的增大呈现先增大后减小的趋势，并在支阀道宽度Bt=1.9 mm左右时达到最大. 同时基于对泄漏量的考虑，最优支阀道宽度建议取值区间为Bt=1.7~2.1 mm.

(3)阀槽半径Rv

Fig. 11 Influence of branch valve width on opening force and leakage rate (h=3 μm, hg=4 μm, P=2 MPa, N=40000 r/min)图11 支阀道宽度对开启力和泄漏量的影响

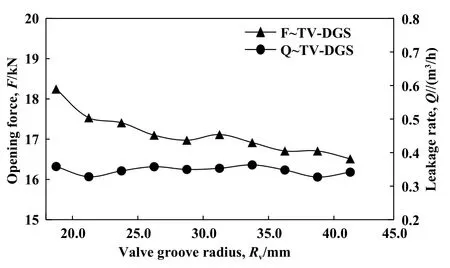
Fig. 12 Influence of valve groove radius on opening force and leakage rate (h=3 μm, hg=4 μm, P=2 MPa,N=40000 r/min)图12 阀槽半径对开启力和泄漏量的影响

阀槽半径决定了特斯拉槽型的流线型程度，半径的大小对密封性能也有一定的影响，如图12所示，在研究参数范围内，泄漏量对阀槽半径变化的敏感度较低，泄漏量变化不大；而随着阀槽半径的增大，开启力呈明显的下降趋势，考虑到较小的阀槽半径会影响槽型结构和槽数的设计，阀槽半径不宜过小，同时兼顾较大的开启力和低泄漏量，阀槽半径建议选择区间为22.5~32.5 mm，此时的槽型形状更适宜流场流体动压效应的形成.

4 抑扰特性分析

为进一步研究两类槽型的稳定特性及抑扰能力，分别开展同一工况下稳态气膜特性和瞬态膜压波动情况的研究. TV-DGS和S-DGS在同一工况和不同膜厚时的气膜稳态性能参数列于表3中，对比结果可知，不同膜厚下TV-DGS的开启力及气膜刚度均较S-DGS有一定提升，这一结果实现了对经典螺旋槽型干气密封性能的进一步突破. TV-DGS的泄漏量较螺旋槽略有增加，经计算，在干气密封气膜稳定区间(膜厚h≈3~6 μm[42-43])内，TV-DGS相对S-DGS的刚度提升近20%，这对于干气密封的稳定运行具有重要意义.

表3 不同气膜厚度下气膜性能参数比较(hg=4 μm,P=2 MPa, N=30000 r/min)Table 3 Comparison of film performance parameters with different film thicknesses

瞬态膜压波动情况与微尺度密封流场稳定性密切相关，较大的膜压波动有可能造成流场的微振动，不利于流场气膜和密封的稳定性，这里采用瞬态膜压波动幅值进行表征，公式如下[39].

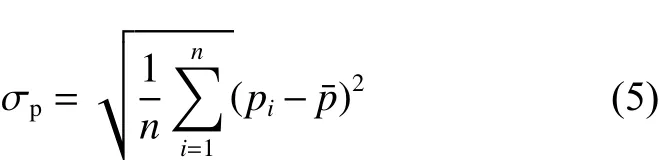
式中：pi为密封端面任意时刻的压力值，p¯为整个迭代计算时间段的平均压力值.

图13所示为不同转速下两种槽型的瞬态膜压波动幅值方差计算结果，由图13可知，TV-DGS较S-DGS的整体压力波动幅值偏小且更加稳定，TV-DGS的膜压波动幅值方差在不同转速时都处于较低(Pv＜0.4)的水平. 随着转速的增大，TV-DGS的稳定性更好，当转速超过30 000 r/min时，S-DGS的膜压波动幅值方差随转速的升高持续增大，而TV-DGS的相应方差值持续稳定在较低水平，由此可知，转速越高，TV-DGS的气膜稳定性越好.

Fig. 13 Comparison of amplitude variance of transient pressure fluctuation with different rotation speeds (h=3 μm,hg=4 μm, P=2 MPa)图13 不同转速下瞬态膜压波动幅值方差对比

5 Taguchi分析

Taguchi方法的提出多是为了解决各种工程的优化问题[44]，凭借其实用性强、高效且系统性强的特点，已被广泛应用于多参数优化设计试验中[45]. 为系统探讨工况参数及TV-DGS各类几何参数对密封性能的影响权重情况，基于Minitab软件及Taguchi方法，选取3类工况参数及三种槽型参数进行模拟试验. 鉴于阀槽半径对密封性能影响不显著，取阀槽半径Rv=30 mm时进行Taguchi分析，具体因子列于表4中.

表4 6因子5水平试验表Table 4 6 factors 5 levels experimental table

根据表4数据，需进行25组模拟试验，首先按照设计表进行仿真计算，得出结果后利用Minitab软件对数据进行处理分析，可得到各因子对密封开启力和泄漏量的影响曲线及权重结果. 图14所示为开启力的影响情况，其响应值列于表5中，由表5可知，各因子影响程度的大小顺序为介质压力＞膜厚＞槽深＞转速＞支阀道＞主阀道. 由图14可以看出，当各因子分别为P=4.0 MPa，N=30000 r/min，h=3 μm，hg=5 μm，Bm=3 mm和Bt=1.3 mm时，此时的开启力为相应区间的最大值.

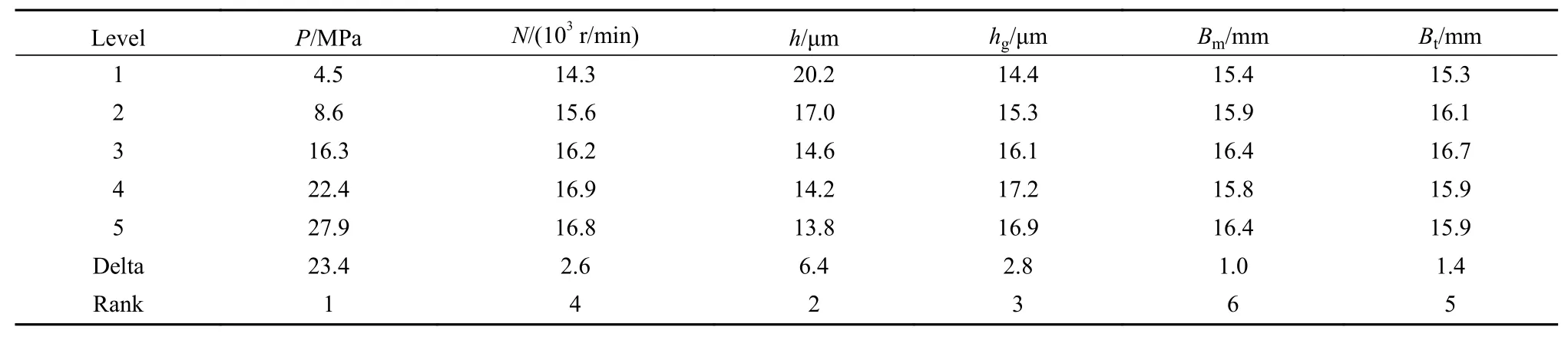
表5 开启力响应表Table 5 Response table for opening force

图15所示为各因子对TV-DGS泄漏量的影响曲线及权重结果，其响应值列于表6中，由表6可知，各因子对泄漏量的权重影响与开启力略有不同，影响程度的大小排序为介质压力＞膜厚＞转速＞槽深＞主阀道＞支阀道，主要区别在于膜厚、转速及主支阀道的权重区别.分析图15可以看出，压力和膜厚对泄漏量的影响均很大，泄漏量最大值对应的各个参数因子分别为P=4.0 MPa，N=10 000 r/min，h=7 μm，hg=4 μm，Bm=2 mm和Bt=0.5 mm.

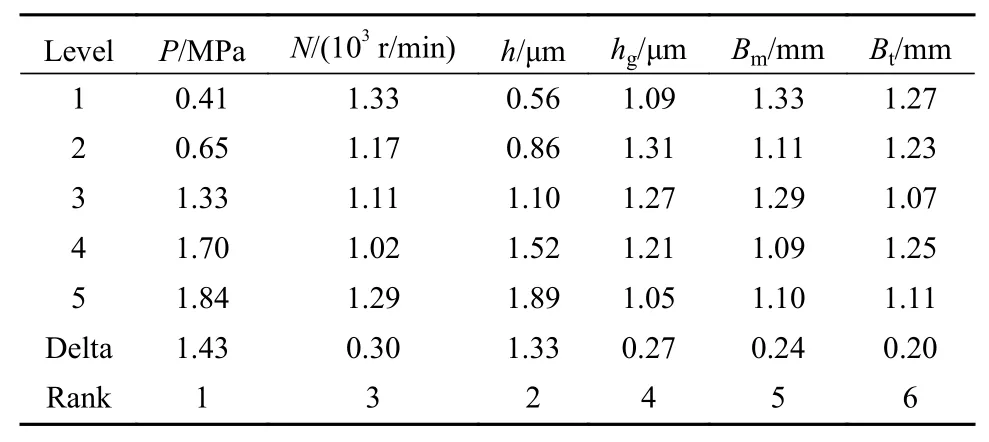
表6 泄漏量响应表Table 6 Response table for leakage rate

综上可知，各影响因子对开启力和泄漏量的影响规律和权重略有区别，对应开启力和泄漏量最大值的各参数因子差别较大. 压力和膜厚对密封性能的影响权重最大，转速对泄漏量的敏感程度更高，主支阀道的尺寸对密封性能的影响最小.

6 结 论

a. 依据特斯拉阀结构设计的新型特斯拉阀型流体动压机械密封对于进一步提升密封性能有积极作用，TV-DGS与传统S-DGS相比，尤其在高速、小膜厚及大槽深时，开启力提升效果更加显著.

b. 在干气密封正常运行膜厚区间内，TV-DGS较传统S-DGS性能优势显著，气膜刚度提升效果明显，有利于进一步提高干气密封稳定性.

Fig. 14 Influence degree of each parameter factors on the opening force of TV-DGS图14 各参数因子对TV-DGS的开启力影响程度

Fig. 15 Influence degree of each parameter factors on the leakage rate of TV-DGS图15 各参数因子对TV-DGS泄漏量影响程度

c. 特斯拉槽型的优良性能主要在于单向导通和局部多点集聚特性的引入，进一步提高了高压面积区域，是此类新型槽型密封性能得以全面提升的关键因素，主阀道、支阀道及阀槽半径分别具有最优值区间.

d. 基于Taguchi设计及用Minitab软件的多参数系性分析，在研究范围内主、支阀道参数对密封性能影响最小，压力和膜厚对开启力和泄漏量的影响最大.