微重力环境下硅基纳米器件碰撞滑动接触问题研究
王云峰, 佟瑞庭*, 张 涛, 杜晶涛, 韩 宾, 刘 更
(1. 西北工业大学 陕西省机电传动与控制工程实验室, 陕西 西安 710072;2. 中国运载火箭技术研究院, 北京 100076;3. 江苏自动化研究所, 江苏 连云港 222006)
随着微纳米技术的飞速发展,微机电系统广泛应用于微纳卫星、皮卫星以及各种高精密仪器[1]. 由于严重的尺寸效应,其表面黏着力和摩擦力等相对于传统机械中的体积力更为突出[2]. 空间环境中,微重力环境使运动部件易受到轻微扰动产生不规则的碰撞,从而引起碰撞摩擦[3],进一步影响其摩擦性能. 因此研究微重力环境下微纳器件的摩擦性能对提高航天器的稳定性具有重要意义.
宏观机械振动会影响摩擦的滑动和黏滑方式,有时会引起摩擦力急剧下降[4-8];原子力显微镜试验证实振动同样影响微观摩擦过程[9-11];分子动力学(Molecular dynamics, MD)模拟在进行原子尺度现象定量分析的同时,可以观察材料内部动态变化,越来越多的学者采用MD进行纳米摩擦学研究. 王星等[12]采用MD模拟了纳米SiO2颗粒与单晶硅表面的碰撞过程,结果表明一定的碰撞速度造成了基体碰撞区域原子排布发生变化,导致了晶格的畸变. Cheng等[13]通过MD模拟研究了振动对纳观摩擦的影响,研究表明适当的振动可以增大作用面间的距离,显著降低平均摩擦力的大小. Wang等[14]通过MD模拟研究了横向振动对硅基材料纳观摩擦的影响,阐明了横向激励引起动态超滑的原因,他们发现固有频率下平均摩擦力随振幅的增加而大大降低;非固有频率下较大的振幅也可实现动态超滑.
近年来大量研究结果表明,具有特定结构特征的纹理表面表现出更优异的摩擦学特性[15-16],纹理表面减摩技术受到了国内外学者的广泛关注. Schreck等[17]和Pettersson等[18]研究了凹坑纹理的减摩效果,发现凹坑纹理具有储存润滑油的作用,显著减小了摩擦力.南江红等[19]采用MD模拟研究了不同纹理方向和密度对摩擦力的影响. 王新宇等[20]将管道内表面织构化处理,表明优化织构密度和直径可以提升管道内壁类金刚石涂层(Diamond-like carbon, DLC)的摩擦学性能.吕文斐等[21]研究了不同润滑状态下纹理表面的摩擦学特性,发现只有在特定条件下纹理的引入才会提升材料的摩擦学性能. Tong等对不同的基体材料(Cu[22]和Ag[23])进行了纹理表面滑动接触研究,分析了不同纹理形状、方向及密度等对平均摩擦力的影响.
本文中针对微重力环境下微纳器件的碰撞滑动接触问题,利用MD模拟,研究碰撞滑动接触摩擦机理以及纹理表面在碰撞滑动接触中的减摩效果,为微纳器件表面抗黏减摩设计提供理论基础和科学指导,使微纳器件更好地应用于航天领域.
1 分子动力学模型的建立
微重力环境下硅基纳米器件碰撞滑动接触的分子动力学模型如图1所示,图中描述了金刚石压头与硅基体之间的碰撞滑动接触过程. 硅基体在X、Y和Z方向上的尺寸为50a×16a×25a,其中a为硅的晶格常数(a=5.43 Å);X、Y和Z方向分别对应硅的[100]、[010]和[001]晶向;金刚石圆柱压头半径为8a. 由于压头上端原子与基体无相互作用,为了提高计算效率,仅保留压头下端原子进行计算. 图1所示的试件中共有193 095个原子,其中压头包含有30 679个碳原子,基体包含有162 416个硅原子.

Fig. 1 Molecular dynamics model图1 分子动力学模型
硅基体分为牛顿层、恒温层和固定层,其中恒温层和固定层的厚度分别为2a和a,模拟的时间步长设置为1 fs,模型的初始温度为300 K,模拟过程中将恒温层的温度保持在300 K. 根据Maxwell-Boltzmann能量分布函数[24]为建立的压头和基体分配初始速度,该速度对应于它们平衡状态的温度,可以表示为

其中:E为总能量,k为玻尔兹曼常量,fE(E)为原子在E和E+dE之间的动能.
完成每个原子速度和位置初始化后,在NVT系综下,初始温度为300 K,对压头和基体原子进行热平衡和弛豫处理. 完成弛豫之后,在NVE系综下开始碰撞滑动接触过程模拟. 结合微重力环境机构的运动特性:轴旋转过程中总是伴随着不规则的碰撞,将轴和孔的无规则碰撞等效为压头在Y和Z方向的强迫正弦振动,Y和Z方向的振幅分别为Ay与Az,频率分别为fy与fz;将轴的旋转运动等效为压头在基体表面沿X方向的滑动,给定滑动速度Vs=50 m/s;基体底部连接有刚度系数为K的弹簧来模拟微重力环境下基体随压头振动产生的随动过程. 根据公式(其中K为弹簧刚度系数,M为基体质量),可求得基体的固有频率为36.6 GHz.
该分子动力学模型中,存在三种不同的相互作用势:Si-Si原子、C-C原子及C-Si原子之间的相互作用.由于金刚石压头的硬度远大于单晶硅基体,因此将金刚石压头视为刚体,从而忽略C-C原子之间的相互作用;同时参考相关文献,对于具有金刚石立方结构的共价体系,应该考虑其共价键和键角的影响,Tersoff多体势函数在这方面具有独特的优势[26],因此采用Tersoff多体势函数描述Si-Si原子之间的相互作用,其基本表达式为

其中E和Vij分别为原子的总能量和键能.Vij可以通过截断函数fc、排斥对电位fR以及吸引对电位fA函数来定义,可以表示为
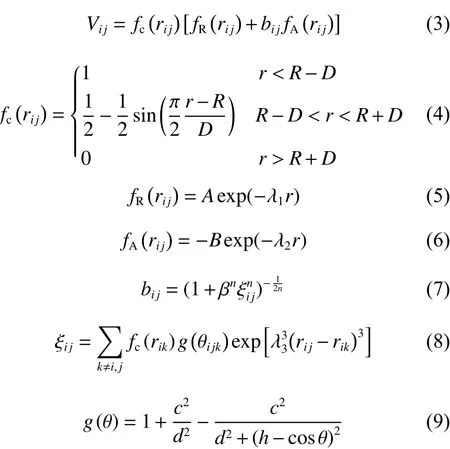
其中:i,j和k是系统内原子,rij为原子i和j之间的键长,θijk为i-j键与i-k键之间的键角;r为原子之间的距离;R为截断半径;D为截断半径参数;bij为原子i和j之间的键级,是化学键强度的度量;ξij为有效配位数;λ1、λ2和λ3为吸引和排斥项对偶势势能曲线梯度系数;其余参数列于表1中.
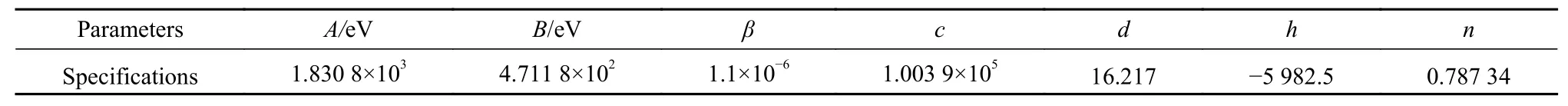
表1 Si的Tersoff势函数参数表[27]Table 1 Parameter of Tersoff potential[27]
金刚石压头和硅基体原子之间的相互作用使用Morse势[28]来描述,其基本表达式为

其中D,a和r0为根据试验数据确定的经验参数.D为结合能系数,a为弹性模量,rij为原子间瞬时距离,r0为原子间作用力为零时的距离. 在本研究中所使用的CSi的Morse势函数的参数D=0.435 eV,a=46.487 nm-1,r0=0.19475 nm.
本工作中采用Sandia国家实验室开发的开源软件LAMMPS进行分子动力学模拟,仿真过程中采用Verlet积分算法,利用OVITO软件对模拟结果进行可视化分析,主要的模拟参数列于表2中.

表2 分子动力学仿真参数Table 2 Molecular dynamics simulation parameters
2 结果与讨论
2.1 光滑表面下不同振动频率对碰撞滑动接触的影响
振幅A和频率f是描述振动的两个重要参数,其中垂直于接触表面的振动对碰撞滑动摩擦过程的影响更为显著[5],本文中的研究也证实了这一结论.
图2所示为无振动、Y+Z方向、Y方向振动及Z方向振动四种工况下碰撞滑动平均摩擦力对比. 由图2可以看出:Y方向或Z方向的振动都具有减小摩擦力的效果;Y方向振动对碰撞滑动摩擦过程影响较小,在仅有Y方向振动的工况下平均摩擦力相较于无振动工况略有下降;相较而言,Z方向的振动(垂直于接触表面的振动)对碰撞滑动摩擦过程的影响更为显著. 同时存在Y方向和Z方向振动工况下平均摩擦力大小与仅有Z方向振动工况下的数值基本持平,说明在该工况下Z方向振动对碰撞滑动接触平均摩擦力起主导作用. 因此在仿真过程中,依据单一变量原则,通过更改fz的值来研究Z方向振动频率对光滑表面碰撞滑动接触的影响.
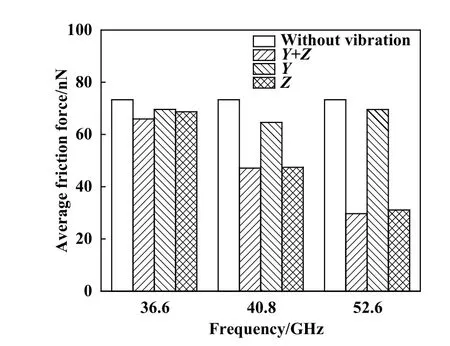
Fig. 2 Average friction force of vibration in different directions图2 不同方向振动平均摩擦力对比
设定Ay和Az为0.55 nm,fy为50 GHz保持不变,依据固有频率的大小,选取21组Z方向振动频率,包含压头无振动状态、低于固有频率以及高于固有频率三种状态下的平均摩擦力进行比较,如图3所示. 可以看出振动的存在使得平均摩擦力有不同程度的降低;振动频率低于固有频率时,平均摩擦力与压头振动频率fz之间没有明显的关系;当fz大于固有频率时,随着压头振动频率fz的增大,平均摩擦力呈现出先减小后保持不变的趋势,最终平均摩擦力保持在30 nN. 为了便于分析每个阶段Z方向振动频率对碰撞滑动接触的影响机理,选取固有频率fz=36.6 GHz、平均摩擦力减小阶段的频率fz=40.8 GHz和基本保持不变阶段的频率fz=52.6 GHz三种工况对碰撞滑动接触过程进行分析,探究不同阶段的摩擦机理.
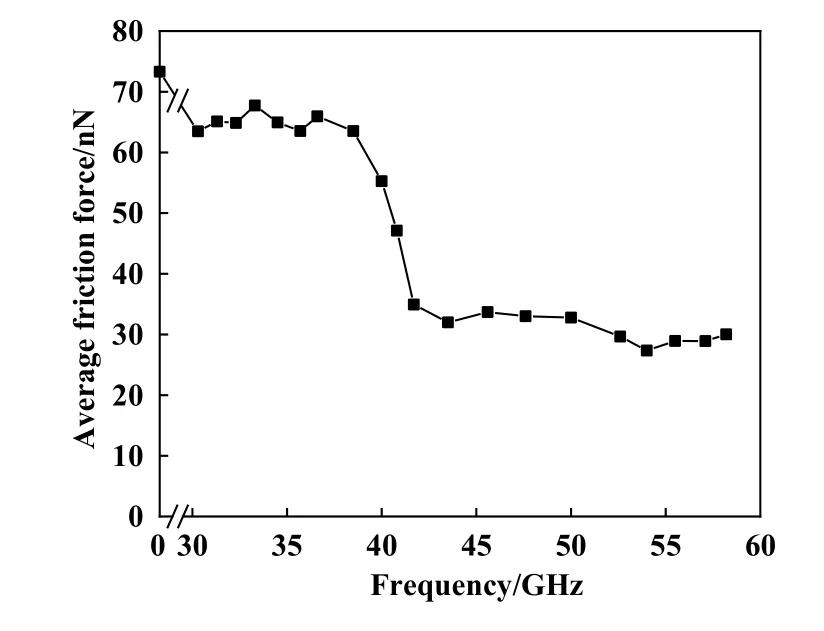
Fig. 3 Average friction forces at different frequencies图3 不同频率下的平均摩擦力
为了更好地理解平均摩擦力的频率依赖性,提取压头与基体表面之间的相对位置关系,进而得到不同振动频率下压头的压入状态,了解平均摩擦力随振动频率变化的规律. 图4所示为三种工况下压头与基体之间相对坐标差曲线,定义相对坐标差为压头Z方向最小坐标与基体非接触区域表层原子Z方向坐标的差值,相对坐标差为0表示压头刚好与基体表面接触,为负值表示压头压入基体,为正值表示压头与基体处于分离状态. 图5给出了fz为36.6、40.8和52.6 GHz时压头与基体的振动曲线. 图6所示为三种工况下碰撞滑动接触过程压头与基体实际接触时间对比.

Fig. 4 The coordinate difference between the indenter and the surface of the substrate图4 压头与基体表面之间的相对坐标差曲线
如图5(a)所示,当fz=36.6 GHz时,压头的振动频率等于基体固有频率,压头与基体共同振动. 从图4可以看出当压头振动频率与基体固有频率相同时,二者相对坐标差曲线在初始阶段波动较大,当滑动距离达到30 Å后,压头与基体之间的相对坐标差曲线逐渐收敛,最终与无振动工况相似,且从图6可以看出,振动的存在减小了压头与基体的实际接触时间,因此,在图3中,与无振动工况相比,36.6 GHz处的平均摩擦力略有下降. 当fz为40.8和52.6 GHz时,压头与基体之间不存在共同振动现象,观察图4可以发现fz=40.8 GHz的工况下,压头滑动距离达到60 Å后,相对坐标差曲线幅值有所下降. 然而fz=52.6 GHz工况下,由图5(c)可知基体的随动滞后于压头振动,二者的振动曲线存在偏离,结合图4可知,该振动频率下压头与基体相对坐标差曲线始终维持较为剧烈的波动,且相较于无振动工况而言,fz为40.8和52.6 GHz时压头与基体实际接触时间有明显减小(图6),因此与无振动工况相比,平均摩擦力显著降低.
在碰撞滑动过程中,基体表层原子的温度最具代表性,因此图7仅给出了三种工况下基体表层原子的温度. 从图7可以看出,fz=36.6 GHz时,基体表层温度在滑动过程初始阶段较高,当滑动距离达到30 Å后,基体表层温度稳定在350 K左右基本不变,该频率下基体表层温度变化趋势与图4中fz=36.6 GHz时压头与基体相对坐标差曲线趋势一致;当fz=40.8 GHz时,基体表层温度在开始阶段维持在400 K左右,滑动距离达到100 Å时,基体表层温度逐渐下降到350 K左右,变化趋势同该频率下的相对坐标差曲线趋势相似,因此压头与基体之间的碰撞程度影响了基体表面温度;当fz=52.6 GHz时,相较于其他两种工况,该振动频率下基体表层温度显著增加且呈现出增长趋势,由图3可知该频率下的平均摩擦力显著降低,因此基体表层

Fig. 5 The vibration curves of the indenter and the substrate图5 压头和基体振动曲线
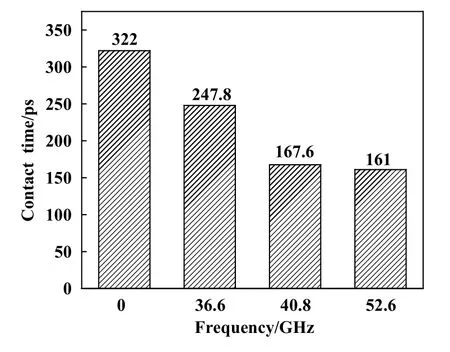
Fig. 6 Contact time between indenter and substrate图6 压头与基体接触时间

Fig. 7 Atomic temperature on the surface of the substrate under different indenter vibration frequencies图7 不同压头振动频率下基体表层原子温度
温度的升高导致基体表层材料的软化也是平均摩擦力减小的原因之一.
剧烈的碰撞使得硅基体内出现其他的相,如Si-II、Si-XI和Si-V. 已有文献[28]报道硅原子之间的距离变化导致了硅的相变. 正常状态下,4个相邻硅原子之间的距离为2.35~2.43 Å,原子分布在2.58 Å范围内,原子之间距离的变化与硅原子配位数从4变化到6有关[29].表3列出了Si-I、Si-II、Si-XII、Si-III和Bct-5五种硅相原子之间的距离和配位数[30].

表3 硅的各种高压相[30]Table 3 Various high-pressure phases of silicon[30]
图8所示为碰撞滑动接触过程中硅基体原子相变统计图,从图8可以看出,当fz=52.6 GHz时基体原子相变数量较多,结合该频率下相对坐标差曲线存在较大的峰值(图4),表明碰撞滑动接触过程中压头压入深度较大,这与文献[30]中压入深度对基体受损层的深度具有决定性影响的结论一致. 在fz=36.6 GHz工况下,因发生共同振动现象,基体和压头的振动频率以及幅值基本一致,可以看出基体表层失效原子数较少,且相变不明显.

Fig. 8 The atomic phase change statistics of substrate during collision sliding contact: (a) 36.6 GHz; (b) 40.8 GHz; (c) 52.6 GHz图8 碰撞滑动接触过程中硅基体原子相变统计图:(a) 36.6 GHz;(b)40.8 GHz;(c)52.6 GHz
硅基体的瞬态结构缺陷横截面如图9所示,其中Si-I由蓝色原子表示,Si-II (位错原子和表面缺陷原子)由灰色表示. 由图9可知,不同的振动频率基体受损层的深度有很大差异. 当fz=36.6 GHz时,因共同振动现象的存在,基体表层原子在碰撞过程中未出现明显的结构缺陷,失效原子数较少;当fz=40.8 GHz时,基体表层原子出现了较为明显的瞬态结构缺陷,失效原子数目较固有频率下也有所增加;当fz为52.6 GHz时,在碰撞的瞬时,硅基体内失效原子数明显高于其他两种工况,高的振动频率造成了基体表面原子的大量失效,失效导致基体表层原子存储的弹性势能被释放,硅基体表面变形松弛,基体表面材料变软,剪切模量降低[31],由图3可知,该工况下平均摩擦力显著降低,因此碰撞导致的基体原子晶格结构的破坏也是平均摩擦力显著降低的原因之一.
2.2 振幅对碰撞滑动接触的影响

Fig. 9 The cross-sectional view of a transient defect structure图9 瞬态结构缺陷横截面图
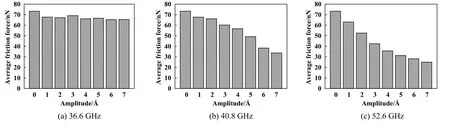
Fig. 10 The average friction forces at different amplitudes图10 不同振幅下的平均摩擦力
选取fz为36.6、40.8和52.6 GHz三种工况对碰撞滑动接触过程进行分析,探究振幅对碰撞滑动接触的影响. 图10所示为三种工况下不同压头振幅的平均摩擦力. 图11所示为三种工况不同振幅下失效原子数目对比. 固有频率下,由于压头与基体发生共同振动现象,即使增大振幅,失效原子数目也不会发生显著变化(图11),因此增大压头的振幅对平均摩擦力的影响较小[图10(a)]. 当压头的振动频率为40.8 GHz时,不存在共同振动现象,增大振幅可以减小平均摩擦力. 这是因为振幅的增加导致更激烈的碰撞,基体表层原子受损程度随振幅增加而增大,致使硅原子晶格结构受到破坏,减小平均摩擦力的犁沟分量,降低平均摩擦力[图10(b)]. 当压头的振动频率为52.6 GHz时,随着压头振幅从0 Å增大到7 Å,平均摩擦力随振幅的增加显著降低[图10(c)],其平均摩擦力减小机理与振动频率为40.8 GHz时相似,但如图11所示,在同等振幅条件下,振动频率为52.6 GHz时失效原子数目较其他两个频率显著增加,因此该频率下,基体对压头的振动更为敏感,增大振幅形成更多的失效原子,破坏原有的晶格结构,导致基体表层原子存储的弹性势能被释放,使得基体剪切模量降低,从而减小摩擦力的犁沟分量,使得平均摩擦力显著降低.

Fig. 11 Number of defective atoms in three cases with different amplitudes图11 三种工况不同振幅下失效原子数目对比
图12所示为不同压头振幅表层温度对比. 图12(a)中fz=36.6 GHz工况下,增加压头振幅对基体表层温度无明显影响;fz=40.8 GHz工况下,压头振幅为1 Å和4 Å时,基体表层温度均在380 K左右,增大压头振幅到7 Å后,基体表层温度明显增大,该变化趋势与失效原子数目的趋势类似;fz=52.6 GHz工况下,基体表层温度随压头振幅的增加而增加,归因于该工况下压头与基体之间剧烈的碰撞,导致大量原子失效的同时产生高热量,同时对比fz=40.8 GHz工况下的温度曲线以及温度数值可知,52.6 GHz工况下基体表层温度对压头振幅更加敏感.
2.3 纹理表面对碰撞滑动接触的影响
纹理表面等效于去除一部分基体表层材料,使基体表面具有一定形状的纹理. 本节中研究硅基体矩形沟槽纹理表面的摩擦学行为,图13所示为基体纹理化模型,其中A代表纹理宽度,B代表纹理间隔,C代表纹理深度,A=3a,B=C=2a,a为硅的晶格常数(a=5.43 Å).
图14所示为不同振动频率光滑表面和纹理表面之间的平均摩擦力对比,纹理表面有效减小了滑动接触过程的平均摩擦力,并且纹理表面随振动频率的变化趋势与光滑表面的变化趋势类似. 对比可知,一定振动频率工况下纹理表面的减摩效果更为显著,无振动工况下纹理表面相对于光滑表面平均摩擦力减小约19.7%,振动频率增大至40 GHz时,纹理表面的引入使得平均摩擦力减小约45%,当振动频率增大至43.5 GHz时,纹理表面相对于光滑表面平均摩擦减小约19.8%. 因此,相较于压头无振动工况,振动频率在36.6~43.5 GHz频率段内,较低振动频率下纹理表面的减摩效果更为显著.
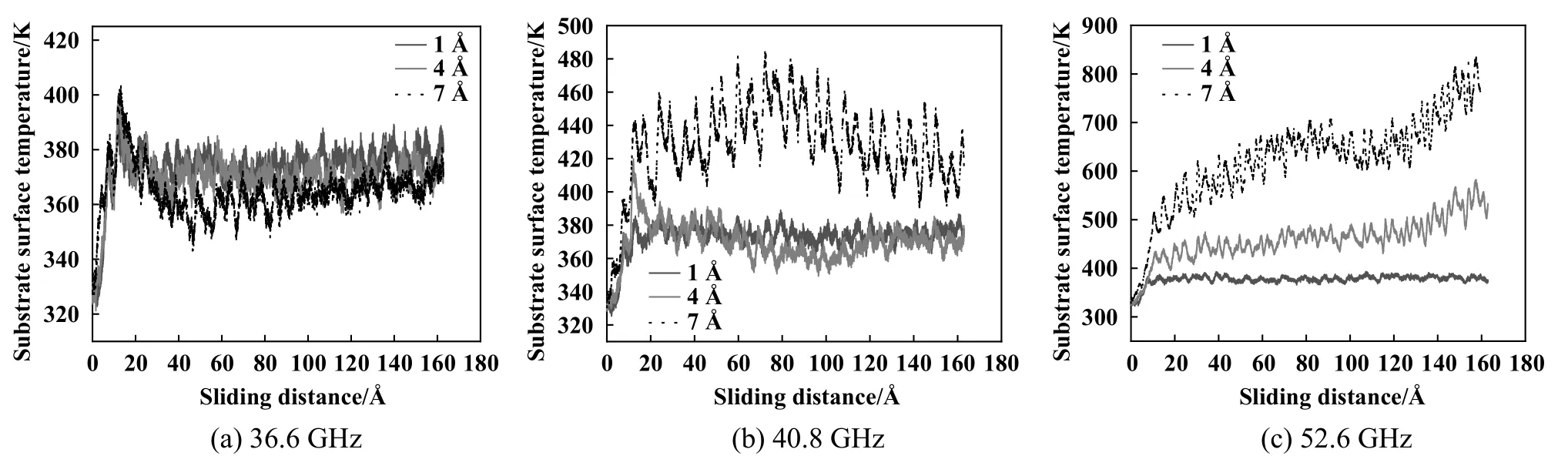
Fig. 12 Comparison of surface temperature with different indenter amplitude图12 不同压头振幅表层温度对比
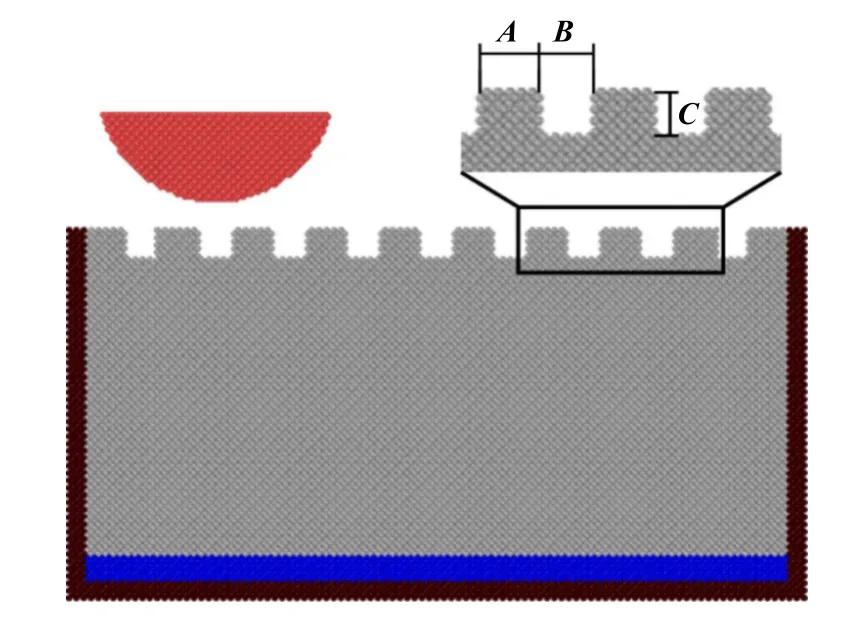
Fig. 13 Textured surface model图13 基体纹理化模型
图15所示为单晶硅纹理表面不同振动频率下基体瞬时温度对比. 从图15可以明显看出振动频率增至41 GHz时,压头碰撞导致基体与压头接触区域温升较高,较高的温升导致基体表层材料软化,剪切模量降低,从而降低平均摩擦力. 此外,当振动频率为36.6 GHz时,压头滑过的区域仍可看到较为明显的纹理,而当振动频率达到41 GHz时,较为剧烈的碰撞导致纹理表面的失效,压头滑过的区域纹理几乎完全消失. 可见较低振动频率下平均摩擦力减小的原因主要是纹理表面的存在减小了压头与基体之间的实际接触面积,随着振动频率的升高,碰撞导致接触区域较大的温升,使得基体表层材料软化,减小压头滑动过程的阻力,进而降低平均摩擦力.

Fig. 14 Comparison of the average friction forces between smooth and textured surface图14 不同频率光滑表面与纹理表面平均摩擦力对比

Fig. 15 Comparison of instantaneous temperature of different vibration frequencies图15 不同振动频率瞬时温度对比
通过对碰撞滑动接触过程的分析,发现纹理表面更容易发生变形,这是因为支撑压头的纹理矩形尺寸小且表面积大,使得纹理表面具有较大的自由表面,降低材料的强度,易产生塑性变形,即纹理表面的存在使得基体表面更容易向压头滑动的方向发生变形,基体对压头滑动的阻力减小,从而导致摩擦力的减小.图16所示为纹理表面原子的瞬态结构缺陷横截面图,可以发现纹理间隙的存在可以起到存储基体表面失效原子的作用,进一步减小滑动过程中压头前端的阻力,从而降低平均摩擦力.
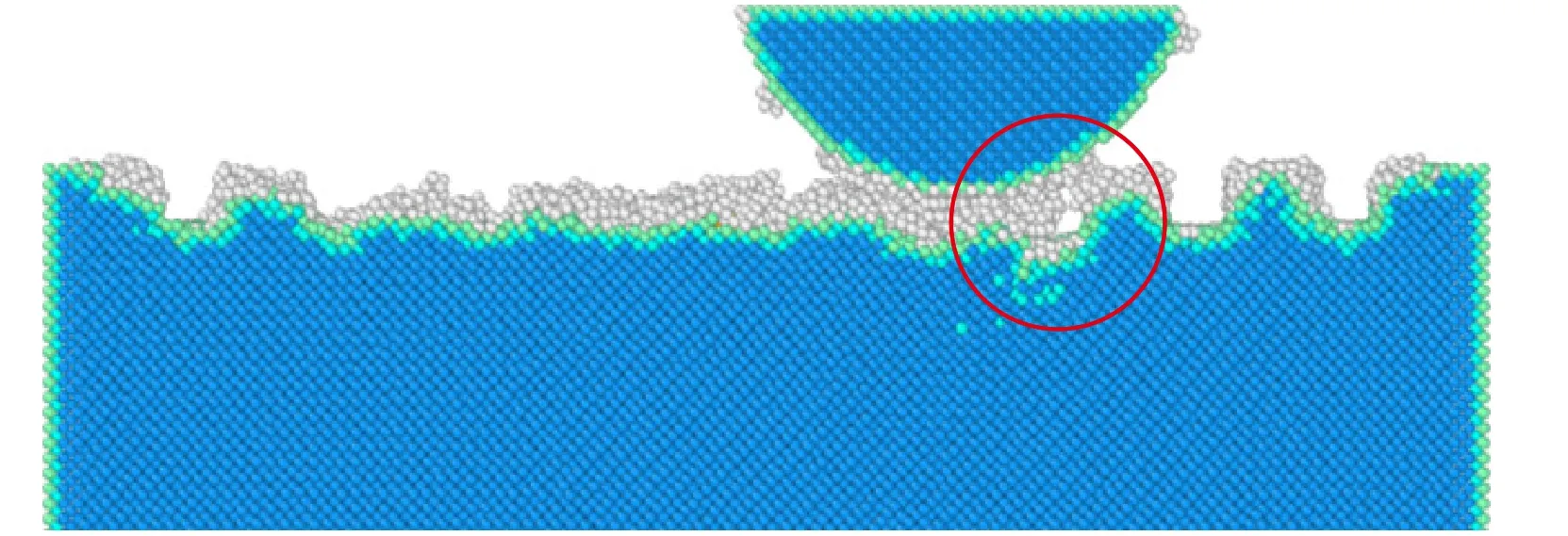
Fig. 16 The cross-sectional view of a transient defect structure of textured surface图16 纹理表面瞬态结构缺陷横截面图
3 结论
a. 碰撞滑动接触平均摩擦力表现出明显的频率依赖性. 随压头振动频率的变化可分为两个阶段:振动频率低于基体固有频率时,平均摩擦力不随压头振动频率的增大发生显著变化;高于固有频率时,平均摩擦力随压头振动频率的增大呈现先减小后不变的变化趋势.
b. 固有频率下,增大压头振动幅值对平均摩擦力和基体表层温度几乎没有影响. 在40.8和52.6 GHz工况下增大振幅提高基体表面温度并导致基体晶格结构的破坏,其中52.6 GHz工况下基体失效原子数目和基体表层温度对压头振幅更加敏感,增大振幅显著降低平均摩擦力.
c. 基体表面引入纹理有效降低碰撞滑动过程中的平均摩擦力. 纹理表面的存在降低压头与基体之间的实际接触面积,此外,随着振动频率的升高,碰撞导致了基体接触区域较大的温升,软化了基体表层材料,剪切模量降低,从而降低了碰撞滑动过程中的平均摩擦力.

